Задания
Версия для печати и копирования в MS Word
Тип 9 № 507884
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
Спрятать решение
Решение.
Виноград содержит 10% питательного вещества, а изюм — 95%. Следовательно, 6 кг изюма содержат 6 · 0,95 = 5,7 кг питательного вещества. Таким образом, для получения 6 килограммов изюма требуется
килограмм винограда.
Ответ: 57.
Аналоги к заданию № 99574: 109061 109071 109105 109109 507884 507907 109063 109065 109067 109069 … Все
Кодификатор ФИПИ/Решу ЕГЭ: Задачи на проценты, сплавы и смеси
Спрятать решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 9 № 507884
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
Аналоги к заданию № 99574: 109061 109071 109105 109109 507884 507907 109063 109065 109067 109069 … Все
Кодификатор ФИПИ/Решу ЕГЭ: Задачи на проценты, сплавы и смеси
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.
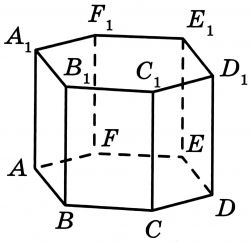
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac19right)^{x+4}=729)
Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)
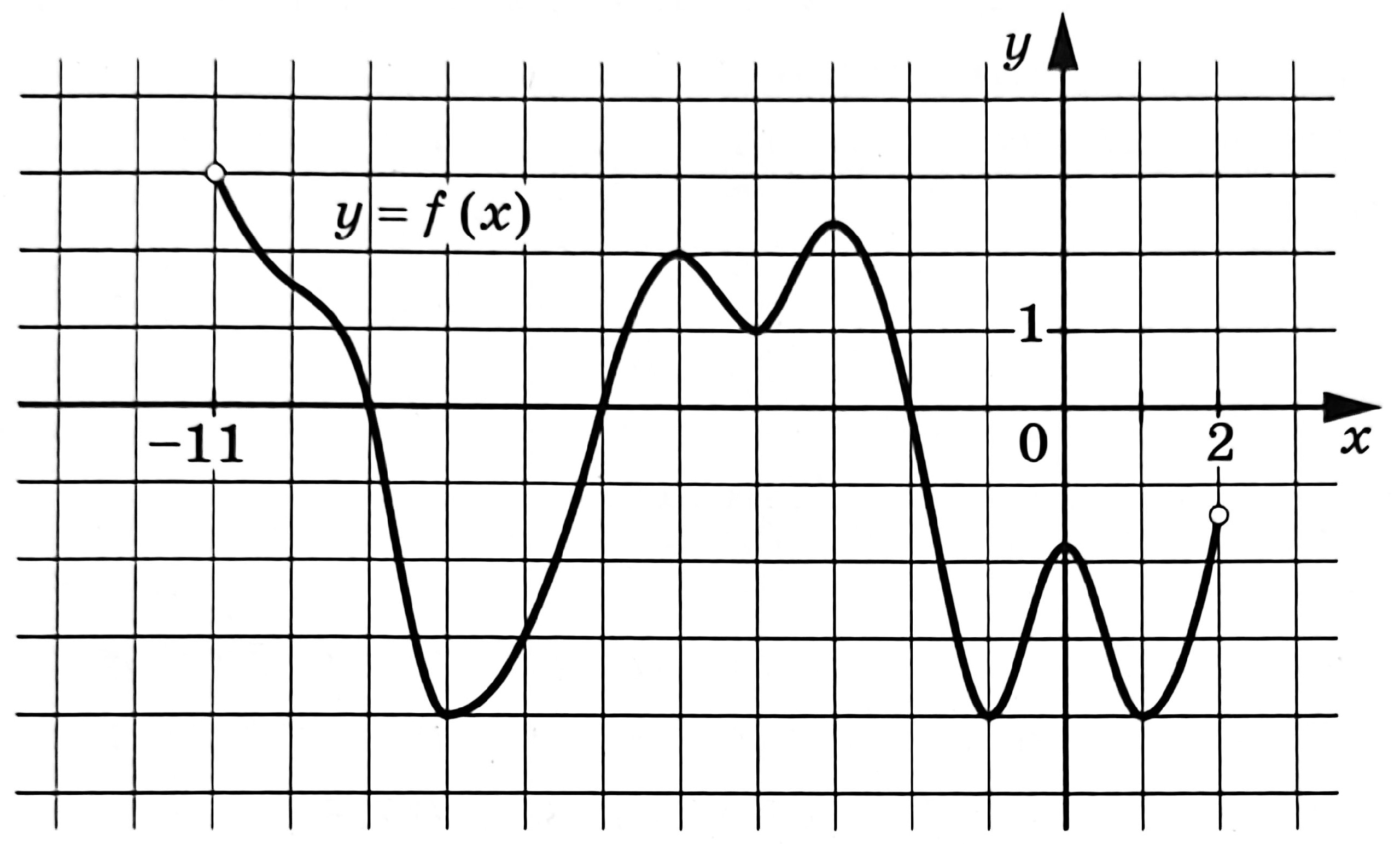
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
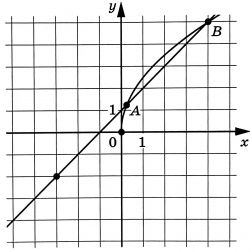
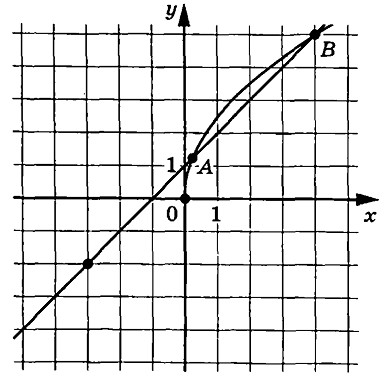
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.
Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])
а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
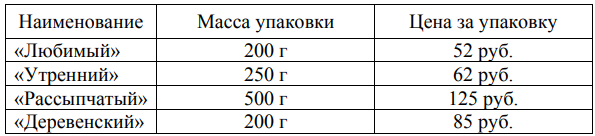
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
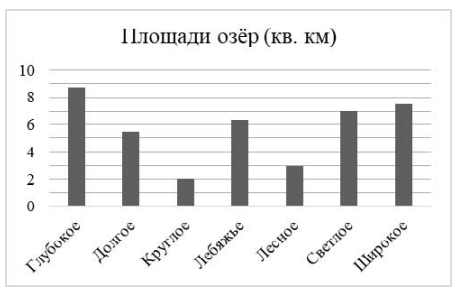
Задание 8.
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
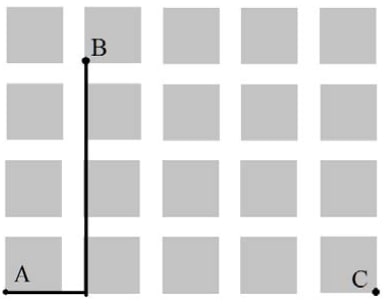
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки. Ответами к заданиям 1–22 являются последовательность цифр, число или слово (словосочетание). Ответы запишите в поля ответов в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ № 1 справа от номеров соответствующих заданий, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Скачать тренировочный вариант ЕГЭ: Скачать
Скачать ответы на тренировочный вариант ЕГЭ: Скачать
Задания:
1. Рассмотрите таблицу «Методы биологических исследований» и заполните ячейку, вписав соответствующий термин. Применяется для выявления геномных мутаций.
2. Исследователь добавлял в стакан коровьего молока желудочный сок собаки. Как спустя час в стакане изменится содержание дисахарида лактозы и животных жиров? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
3. Площадь земель, покрытых лесом, в России составляет примерно 1200 млн га. Известно, что 12 га леса связывают 18 тонн диоксида углерода в год. Сколько млн тонн углекислого газа может быть связано за год за счет российских лесов?
4. Определите вероятность (в %) гибели от анемии ребенка, родившегося в браке гомозиготных по рецессивному аллелю родителей, если эта форма анемии наследуется как аутосомный доминантный признак. В ответ запишите только соответствующее число.
5. Каким номером на рисунке обозначена структура, образующая спираль в сперматозоидах млекопитающих?
6. Установите соответствие между характеристиками и структурами, обозначенными на рисунке цифрами 1, 2, 3, 4: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
7. Выберите три признака, которые соответствуют описаниям селекции. Запишите в таблицу цифры, под которыми они указаны.
1) выведение новых штаммов микроорганизмов
2) получение новых семейств растений
3) получение генномодифицированных растений
4) выведение тритикале при скрещивании пшеницы и ржи
5) получение рекомбинантной плазмиды
6) выведение пород животных и сортов растений
8. Установите последовательность этапов ферментативного катализа. Запишите в таблицу соответствующую последовательность цифр.
1) образование нестабильного комплекса фермент-продукт
2) сближение фермента и субстрата
3) начало распада комплекса фермент-продукт
4) формирование фермент-субстратного комплекса
5) высвобождение продукта и фермента
9. Какой цифрой на рисунке обозначена вторичная полость тела?
10. Установите соответствие между характеристиками и структурами тела дождевого червя, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
11. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Для растения, изображенного на рисунке, характерно:
1) гаметофит обоеполый — содержит архегонии и антеридии
2) дихотомическое ветвление
3) заросток сердцевидной формы
4) споры созревают в сорусах
5) споры образуются в спороносных колосках
6) гаметофит формирует вайи
12. Установите последовательность систематических групп, начиная с самого низкого ранга. Запишите в таблицу соответствующую последовательность цифр.
1) Эукариоты
2) Членистоногие
3) Ежемухи
4) Ежемуха свирепая
5) Двукрылые
6) Животные
13. Какой цифрой на рисунке указан тип научения, который изучал К. Лоренц?
14. Установите соответствие между характеристиками и типами научения, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
15. Выберите три верно обозначенные подписи к рисунку «Строение уха». Запишите цифры, под которыми они указаны.
1) серная (церуминозная) железа
2) наружный слуховой проход
3) слуховая косточка
4) овальное окно
5) преддверно-улитковый нерв
6) улитка
16. Установите последовательность событий, происходящих при свертывании крови. Запишите в таблицу соответствующую последовательность цифр.
1) разрушение тромбоцитов у места повреждения
2) превращение протромбина в тромбин
3) уплотнение рыхлой пробки тромбоцитов фибриновыми нитями
4) превращение фибриногена в фибрин
5) выделение тромбопластина
6) образование тромба
17. Прочитайте текст. Выберите три предложения, в которых даны описания географического видообразования. Запишите цифры, под которыми они указаны. (1)Видообразование происходит в результате расширения ареала исходного вида или при попадании популяции в новые условия. (2)Такое видообразование называют аллопатрическим. (3)Примером видообразования служит формирование двух подвидов погремка большого на одном лугу. (4)Естественный отбор способствовал формированию двух рас севанской форели, нерестящихся в разное время. (5)Репродуктивная изоляция особей не является обязательным условием видообразования. (6)Результатом изоляции является формирование эндемичных островных видов животных.
18. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Примеры антропогенных факторов воздействия:
1) разрушение озонового слоя под действием фреонов
2) гибель сусликов из-за пандемии
3) нарушение режима рек под влиянием деятельности бобров
4) разрыхление почв дождевыми червями
5) эвтрофикация водоемов из-за смыва удобрений
6) металлизация атмосферы
19. Установите соответствие между типами взаимоотношений и организмами, между которыми они устанавливаются: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
20. Установите последовательность этапов эволюции животных, начиная с самых древних представителей. Запишите соответствующую последовательность цифр.
1) стегоцефал
2) зверозубый ящер
3) тушканчик
4) сеймурия
5) кистеперая рыба
21. Проанализируйте таблицу «Роль прокариотов в экосистемах». Заполните пустые ячейки таблицы, используя элементы, приведённые в списке. Для каждой ячейки, обозначенной буквой, выберите соответствующий элемент из предложенного списка. Список элементов:
1) Редуценты
2) Бактерии-хемосинтетики
3) Продуценты
4) Гетеротрофы
5) Бактерии-фотосинтетики
6) Денитрифицирующие
7) Автотрофы

22. Проанализируйте диаграмму, отражающую содержание холестерола ЛПНП (липопротеинов низкой плотности) в плазме крови обследованных в лаборатории людей. Выберите все утверждения, которые можно сформулировать на основании анализа представленных данных. Запишите в ответе цифры, под которыми указаны выбранные утверждения.
1) Пятеро из обследованных людей имеют значение содержания холестерола-ЛПНП в интервале от 200 до 249 мг/дл.
2) Более 60% пациентов имеют чрезвычайно высокий риск развития атеросклероза.
3) Значение содержания холестерола-ЛПНП более 300 мг/дл смертельно.
4) Более 50% обследованных людей имеют от 75 до 149 мг/дл холестеролЛПНП в плазме крови.
5) В плазме крови 4% людей содержание холестерола-ЛПНП находится в пределах от 50 до 74 мг/дл.
23. Какая переменная в этом эксперименте будет зависимой (изменяющейся), а какая — независимой (задаваемой)? Объясните, как в данном эксперименте можно поставить отрицательный контроль. С какой целью необходимо такой контроль ставить? * Отрицательный контроль – это экспериментальный контроль, при котором изучаемый объект не подвергается экспериментальному воздействию при сохранении всех остальных условий.
24. Предположите, почему для обработки кукурузных полей используют 2,4- Д. Каким веществом по результату действия на двудольные растения является 2,4-дихлорфеноксиуксусная кислота?
25. Рассмотрите рисунок. Какие пары комплементарных азотистых оснований ДНК отмечены буквами А и Б? При содержании большего количества каких пар азотистых оснований молекула ДНК будет медленнее подвергаться денатурации при воздействии повышенной температуры? Ответ поясните.
26. Некоторые виды лишайников являются трехкомпонентными, то есть включают клетки трех видов организмов: гриба, зеленой водоросли и цианобактерии. Какие функции могут выполнять цианобактерии в составе такого лишайника? Назовите не менее двух. Какие преимущества имеет гриб в составе трехкомпонентного лишайника по сравнению с двухкомпонентным?
27. У животных существует несколько типов брачных отношений, например, моногамия – образование стойких супружеских пар, полигамия – спаривание особи одного пола со множеством партнеров противоположного пола. Большинство видов гнездовых птиц практикуют моногамные отношения, а большинство видов млекопитающих — полигамные. Объясните, почему для гнездовых птиц стратегия моногамного поведения наиболее выгодна. По каким причинам птицы, как правило, не могут практиковать полигамию, как это делают млекопитающие? Ответ поясните.
28. Какой хромосомный набор (n) характерен для клеток мегаспорангия и мегаспоры цветкового растения? Объясните, из каких исходных клеток и в результате какого деления образуются клетки мегаспорангия и мегаспора.
29. Существует два вида наследственной слепоты, каждый из которых определяется рецессивными аллелями генов (а или b). Оба аллеля находятся в различных парах гомологичных хромосом. Какова вероятность рождения слепой внучки в семье, в которой бабушки по материнской и отцовской линиям хорошо видят (не имеют рецессивных генов), а оба дедушки дигомозиготны и страдают различными видами слепоты? Составьте схему решения задачи. Определите генотипы и фенотипы бабушек и дедушек, их детей и возможных внуков.
Вам будет интересно:
ЕГЭ по биологии 11 класс 2023. Новый тренировочный вариант №6 — №221121 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Джинни и Джорджия 1-2 сезон смотреть онлайн
После смерти своего мужа 30 летняя женщина Джорджия Миллер решает начать жизнь с чистого листа. Поэтому она решает переехать в Новую Англию вместе со своими детьми, дочерью Джинни и сыном Остином. Устав от многочисленных переездов, дети искренне желают наконец-то осесть на одном месте и жить, не оглядываясь на прошлое своей матери. Джорджия из-за своих прошлых ошибок вынуждена постоянно менять место жительство. Разный взгляд на будущее приводит к разногласиям и конфликтам между женщиной и её детьми. Несмотря на все неурядицы, Новая Англия понравилась Джинни некоторыми перспективами, поскольку именно здесь юной девушке представилась возможность учиться в элитной школе и общаться с интересными людьми.
Поскольку Джорджия совершила большое количество ошибок в прошлом, она всячески стремится оградить детей от необдуманных поступков и решений. Несмотря на это, женщина до сих пор считает себя молодой девушкой. Поэтому она желает найти того единственного мужчину, с которым она смогла бы прожить всю свою жизнь. Такое легкомысленное поведение матери пугает Джинни, ведь Джорджия всё больше времени, сил и внимания уделяет новым ухажёрам. К каким последствиям приведёт такое поведение женщины?
- Оригинальное название: Ginny & Georgia
- Год выхода: 2021
- Страна: США
- Премьера: 24 февраля 2021
- Режиссер: Аня Адамс, Каталина Агиляр Мастретта, Renuka Jeyapalan
- Перевод: TVShows
- Качество: FHD (1080p)
- Статус сериала: На паузе
-
7.5
7.4
- Актеры: Брианна Хоуи, Антония Джентри, Дизель Ла Торрака, Дженнифер Робертсон, Феликс Маллард, Сара Вайсгласс, Скотт Портер, Реймонд Эблэк, Mason Temple, Кэти Дуглас
- Канал: Netflix
- Жанр: Драма, Комедия
«Джинни и Джорджия» смотреть онлайн бесплатно в хорошем качестве
Смотреть онлайн
Плеер 2
Трейлер
Свет
Добавить в закладки
Подписывайтесь на нашу группу в VK
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Скрыть
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Скрыть
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Скрыть
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Скрыть
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Скрыть
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
Скрыть
Задание 10
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Скрыть