Задания
Версия для печати и копирования в MS Word
Тип 11 № 507908 
Найдите наименьшее значение функции 
Спрятать решение
Решение.
Поскольку функция 
возрастающая, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения выражение 
Квадратный трехчлен 
с положительным старшим коэффициентом достигает наименьшего значения в точке 
в нашем случае — в точке 1. Значение функции в этой точке равно 
Ответ: 49.
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 3.3.3 Квадратичная функция, её график, 3.3.6 Показательная функция, её график, 4.2.1 Применение производной к исследованию функций и построению графиков
Спрятать решение
·
·
Сообщить об ошибке · Помощь
Задания первой части (1-11) профильного ЕГЭ по математике в новом формате 2022.
Все задачи для тестов взяты из открытого банка с сайта mathege.ru. Подборка группы vk.com/egeatom/
Предыдущие варианты:
4ege.ru/tr…
4ege.ru/tr…
| 3661 | а) Решите уравнение 2cos^3(x)=-sin((3pi)/2+x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; 4pi]. Решение  График |
а) Решите уравнение 2cos3 x = -sin(3/2pi+x) ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 12 |  |
| 3626 | а) Решите уравнение (x^2+4x-2)*(4^(3x+1)+8^(2x-1)-11)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-0,5; 0,5]Решение График |
а) Решите уравнение (x2+4x-2)(4^3x+1+8^2x-1-11) = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 12 | |
| 3619 | а) Решите уравнение 5sin(2x)-5cos(x)+14sin(x)-7=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi].Решение График |
а) Решите уравнение 5sin2x — 5cosx + 14sinx — 7 = 0 ! Тренировочная работа №1 по математике 10 класс Статград 08-02-2023 Вариант МА2200109 Задание 12 | |
| 3598 | а) Решите уравнение 2sin^2(pi/2-x)+sin(2x)=0 б) Укажите корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2].Решение График |
а) Решите уравнение 2sin^2(pi/2-x) +sin2x =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 21 Задание 12 | |
| 3595 | а) Решите уравнение 36(log_{1/8}(x))^2+4log_{1/4}(x)-5=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5; 5]Решение График |
а) Решите уравнение 36log2 1/8 x-+ 4log1/4 x — 5 = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 20 Задание 12 # Ошибка в ответе пособия у Ященко : color{red}{sqrt2/2; 4sqrt2} | |
| 3570 | а) Решите уравнение 15^(sin(x))=3^(sin(x))*5^(-cos(x)) б) Найдите все корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi].Решение График |
а) Решите уравнение 15 sinx =3 sinx 5 -cosx ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 12 Вариант МА2210209 | |
| 3561 | а) Решите уравнение cos(2x)+sin(2x)+1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2].Решение График |
а) Решите уравнение cos2x + sin2x +1 = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 12 | |
| 3551 | а) Решите уравнение 25^(x-0.5)-13*10^(x-1)+4^(x+0.5)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-pi/2; pi].Решение График |
а) Решите уравнение 25^ x-0,5 — 13 10^ x-1 +4^ x+0,5 =0! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 12 | |
| 3536 | а) Решите уравнение 2cos(x)*sin(2x)=2sin(x)+cos(2x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2].Решение График |
а) Решите уравнение 2cos x sin 2x =2sinx +cos2x ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 12 | |
| 3528 | а) Решите уравнение (log_{2}(8x^2))^2-log_{4}(2x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8]Решение График |
а) Решите уравнение log2 2(8×2) -log4 (2x) -1 =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 12 | |
Показать ещё…
Показана страница 1 из 36
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
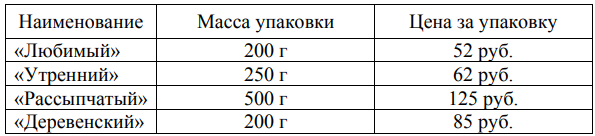
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
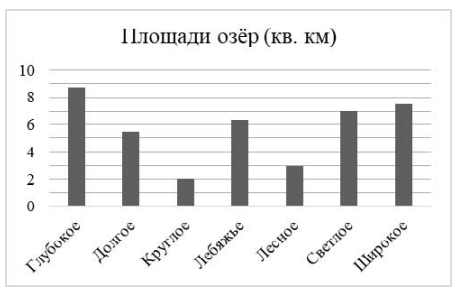
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
1) На плане этого района изображён путь из точки А в точку В. Найдите протяжённость этого пути. Ответ дайте в метрах.
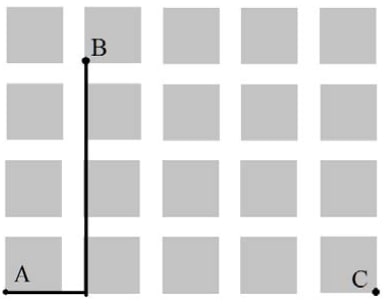
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 14 № 508380
Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:
Приведем другое решение:
Как и в первом решении запишем неравенство в виде:
Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:
Задание 14 № 508380
—>
508780 решу егэ математика.
Ege. sdamgia. ru
07.03.2017 0:00:13
2017-03-07 00:00:13
Источники:
Https://ege. sdamgia. ru/problem? id=508380
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?
Задание 10 № 508782
Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?
Задание 10 № 508783
Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508784
Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508785
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508786
Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508787
Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508788
Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508789
Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508790
Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508786
Задание 10 № 508781
Задание 10 508786.
Ege. sdamgia. ru
14.05.2019 20:28:53
2019-05-14 20:28:53
Источники:
Https://ege. sdamgia. ru/test? likes=508780
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508780
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:
Приведем решение Ирины Шраго.
Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей
—>
Задание 10 № 508780
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
09.08.2017 16:57:34
2017-08-09 16:57:34
Источники:
Https://ege. sdamgia. ru/problem? id=508780