Решу егэ 508213

Задания

Версия для печати и копирования в MS Word

Тип 3 № 508213

Фабрика выпускает сумки. В среднем на 90 качественных сумок приходится 10 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в~магазине сумка окажется с дефектами.

Аналоги к заданию № 508200: 508201 508202 508203 508204 508205 508206 508207 508208 508209 508210 … Все

Прототип задания

·

Источник

Каталог заданий

Версия для печати и копирования в MS Word

1

Тип 3 № 508213

Фабрика выпускает сумки. В среднем на 90 качественных сумок приходится 10 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в~магазине сумка окажется с дефектами.

Аналоги к заданию № 508200: 508201 508202 508203 508204 508205 508206 508207 508208 508209 508210 … Все

Прототип задания

·

Источник

Задача: решите неравенство (x^2-2*x-2)*1/(x^2-2*x)+(7*x-19)*1/(x-3)<=(8*x+1)*1/x

Решение:

* 5 * 5 * 5 * 5 * 5 *

Удачи тебе на экзаменах! У тебя всё получится — мы в тебя верим!

Поделись этой информацией с помощью кнопок ниже (облегчи учёбу другим ученикам, и будет тебе плюс в карму!)

Решение других задач по математике на тему «Рациональные неравенства»

Задание 15 № 507658

Решите неравенство

дробь, числитель — x в степени 2 минус 2x плюс 1, знаменатель — (x плюс 2) в степени 2 плюс дробь, числитель — x в степени 2 плюс 2x плюс 1, знаменатель — (x минус 3) в степени 2 меньше или равно дробь, числитель — (2x в степени 2 минус x плюс 5) в степени 2 , знаменатель — 2(x плюс 2) в степени 2 (x минус 3) в степени 2 .

Решение.

Сделаем замену: a= дробь, числитель — x минус 1, знаменатель — x плюс 2 ,b= дробь, числитель — x плюс 1, знаменатель — x минус 3 . Тогда

a плюс b= дробь, числитель — (x минус 1)(x минус 3) плюс (x плюс 1)(x плюс 2), знаменатель — (x плюс 2)(x минус 3) = дробь, числитель — 2x в степени 2 минус x плюс 5, знаменатель — (x плюс 2)(x минус 3) .

Неравенство принимает вид: a в степени 2 плюс b в степени 2 меньше или равно дробь, числитель — (a плюс b) в степени 2 , знаменатель — 2 , откуда

a в степени 2 плюс b в степени 2 минус 2ab меньше или равно 0 равносильно (a минус b) в степени 2 меньше или равно 0.

Это неравенство выполняется тогда и только тогда, когда a=b. Получаем:

дробь, числитель — x минус 1, знаменатель — x плюс 2 = дробь, числитель — x плюс 1, знаменатель — x минус 3 равносильно x в степени 2 минус 4x плюс 3 = x в степени 2 плюс 3x плюс 2 равносильно x= дробь, числитель — 1, знаменатель — 7 .

Ответ: дробь, числитель — 1, знаменатель — 7 .

Примечание.

Задача допускает решение без замены переменной: тождественными преобразованиями данное неравенство приводится к дробь, числитель — (7x минус 1) в степени 2 , знаменатель — (x плюс 2) в степени 2 (x минус 3) в степени 2 меньше или равно 0, откуда также получается ответ x= дробь, числитель — 1, знаменатель — 7 .

Задание 15 № 508212

Решите неравенство: (x в степени 2 минус 3,6x плюс 3,24)(x минус 1,5) меньше или равно 0.

Решение.

Используя метод интервалов, получаем:

(x минус 1,8) в степени 2 (x минус 1,5) меньше или равно 0 равносильно совокупность выражений новая строка x=1,8, новая строка x меньше или равно 1,5. конец совокупности .

Ответ: ( минус принадлежит fty;1,5>cup{1,8}.

Задание 15 № 507491

Решите неравенство: дробь, числитель — x в степени 2 минус 6x плюс 8, знаменатель — x минус 1 минус дробь, числитель — x минус 4, знаменатель — x в степени 2 минус 3x плюс 2 меньше или равно 0.

Решение.

Перепишем неравенство в виде:

дробь, числитель — x в степени 2 минус 6x плюс 8, знаменатель — x минус 1 минус дробь, числитель — x минус 4, знаменатель — x в степени 2 минус 3x плюс 2 le0 равносильно дробь, числитель — (x минус 4)(x минус 2), знаменатель — x минус 1 минус дробь, числитель — x минус 4, знаменатель — (x минус 2)(x минус 1) меньше или равно 0 равносильно дробь, числитель — (x минус 2) в степени 2 (x минус 4) минус (x минус 4), знаменатель — (x минус 2)(x минус 1) меньше или равно 0 равносильно

равносильно дробь, числитель — ((x минус 2) в степени 2 минус 1)(x минус 4), знаменатель — (x минус 2)(x минус 1) меньше или равно 0 равносильно дробь, числитель — (x минус 1)(x минус 3)(x минус 4), знаменатель — (x минус 2)(x минус 1) меньше или равно 0 равносильно система выражений новая строка дробь, числитель — (x минус 3)(x минус 4), знаменатель — x минус 2 меньше или равно 0, новая строка x не равно 1. конец системы .

Множество решений исходного неравенства: ( минус принадлежит fty;1)cup(1;2)cup[3;4>.

Ответ: 

( минус принадлежит fty;1)cup(1;2)cup[3;4>.

Задание 15 № 508213

Решите неравенство: дробь, числитель — 1, знаменатель — { x минус 1} плюс дробь, числитель — 1, знаменатель — { 2 минус x} меньше или равно 5.

Решение.

Используя метод интервалов, получаем:

дробь, числитель — 5x в степени 2 минус 15x плюс 11, знаменатель — левая круглая скобка x минус 1 правая круглая скобка левая круглая скобка 2 минус x правая круглая скобка le0 равносильно дробь, числитель — 5 левая круглая скобка x минус дробь, числитель — 15 минус корень из { 5, знаменатель — , знаменатель — 10 правая круглая скобка левая круглая скобка x минус дробь, числитель — 15 плюс корень из { 5}, знаменатель — 10 правая круглая скобка }{(x минус 1)(2 минус x)} меньше или равно 0 равносильно совокупность выражений новая строка x меньше 1, новая строка дробь, числитель — 15 минус корень из { 5}, знаменатель — 10 меньше или равно x меньше или равно дробь, числитель — 15 плюс корень из { 5}, знаменатель — 10 , новая строка x больше 2. конец совокупности .

Ответ: ( минус принадлежит fty;1)cup левая квадратная скобка дробь, числитель — 15 минус корень из { 5}, знаменатель — 10 ; дробь, числитель — 15 плюс корень из { 5}, знаменатель — 10 правая квадратная скобка cup(2; плюс принадлежит fty).

Задание 15 № 508345

Решите неравенство: 1 минус дробь, числитель — 2, знаменатель — { |x|} меньше или равно дробь, числитель — 23, знаменатель — x в степени 2 .

Решение.

Приведём выражение к общему знаменателю:

1 минус дробь, числитель — 2, знаменатель — { |x|} меньше или равно дробь, числитель — 23, знаменатель — x в степени 2 равносильно дробь, числитель — x в степени 2 минус 2|x| минус 23, знаменатель — x в степени 2 le0 равносильно дробь, числитель — (|x| минус 1 минус 2 корень из 6 )(|x| плюс 2 корень из 6 минус 1), знаменатель — x в степени 2 le0 равносильно

равносильно дробь, числитель — (|x| минус 1 минус 2 корень из 6 ), знаменатель — x в степени 2 le0 равносильно дробь, числитель — (x минус 1 минус 2 корень из 6 )(x плюс 1 плюс 2 корень из 6 ), знаменатель — x в степени 2 le0.

Предпоследнее преобразование верно, так как модуль не может принимать отрицательных значений.

Получаем минус 1 минус 2 корень из 6 меньше или равно x меньше 0 или 0 меньше xle1 плюс 2 корень из 6 .

Ответ: [ минус 1 минус 2 корень из 6 ;0)cup(0;1 плюс 2 корень из { 6}>.

Задание 15 № 508347

Решите неравенство: дробь, числитель — 6, знаменатель — { x корень из 3 минус 3} плюс дробь, числитель — x корень из 3 минус 6, знаменатель — x корень из 3 минус 9 ge2.

Решение.

Пусть z=x корень из 3 , получаем:

дробь, числитель — 6, знаменатель — { z минус 3} плюс дробь, числитель — z минус 6, знаменатель — z минус 9 ge2 равносильно дробь, числитель — 6(z минус 9) плюс (z минус 6)(z минус 3) минус 2(z минус 3)(z минус 9), знаменатель — (z минус 3)(z минус 9) ge0 равносильно

равносильно дробь, числитель — z в степени 2 минус 21z плюс 90, знаменатель — (z минус 3)(z минус 9) le0 равносильно дробь, числитель — (z минус 6)(z минус 15), знаменатель — (z минус 3)(z минус 9) le0 равносильно совокупность выражений новая строка 3 меньше zle6, новая строка 9 меньше zle15. конец совокупности .

Возвращаясь к исходной переменной, получаем: корень из 3 меньше xle2 корень из 3 или 3 корень из 3 меньше xle5 корень из 3 .

Ответ: ( корень из 3 ;2 корень из { 3}>cup(3 корень из { 3};5 корень из { 3}].

Задание 15 № 508348

Решите неравенство: левая круглая скобка дробь, числитель — 10, знаменатель — 5x минус 21 плюс дробь, числитель — 5x минус 21, знаменатель — 10 правая круглая скобка в степени 2 меньше или равно дробь, числитель — 25, знаменатель — 4 .

Решение.

Сделав замену t= дробь, числитель — 5x минус 21, знаменатель — 10 , получаем:

левая круглая скобка дробь, числитель — 1, знаменатель — t плюс t правая круглая скобка в степени 2 leq дробь, числитель — 25, знаменатель — 4 равносильно минус дробь, числитель — 5, знаменатель — 2 меньше или равно дробь, числитель — 1, знаменатель — t плюс t меньше или равно дробь, числитель — 5, знаменатель — 2 равносильно минус 5 меньше или равно дробь, числитель — 2t в степени 2 плюс 2, знаменатель — t le5 равносильно

равносильно система выражений новая строка дробь, числитель — 2t в степени 2 минус 5t плюс 2, знаменатель — t le0, новая строка дробь, числитель — 2t в степени 2 плюс 5t плюс 2, знаменатель — t ge0 конец системы . равносильно система выражений новая строка левая квадратная скобка begin{array}{l} t меньше 0, дробь, числитель — 1, знаменатель — 2 меньше или равно t меньше или равно 2,end{array}. новая строка левая квадратная скобка begin{array}{l} минус 2 меньше или равно t меньше или равно минус дробь, числитель — 1, знаменатель — 2 , t больше 0 end{array}. конец системы . равносильно совокупность выражений минус 2 меньше или равно t меньше или равно минус дробь, числитель — 1, знаменатель — 2 , дробь, числитель — 1, знаменатель — 2 меньше или равно t меньше или равно 2. конец совокупности .

Возвращаясь к исходной переменной, получаем:

совокупность выражений 5le5x минус 21 меньше или равно 20, минус 20 меньше или равно 5x минус 21 меньше или равно минус 5 конец совокупности . равносильно совокупность выражений дробь, числитель — 26, знаменатель — 5 меньше или равно x меньше или равно дробь, числитель — 41}5, дробь, числитель — {, знаменатель — 1 , знаменатель — 5 меньше или равно x меньше или равно дробь, числитель — 16, знаменатель — 5 . конец совокупности .

Ответ: левая квадратная скобка дробь, числитель — 1, знаменатель — 5 ; дробь, числитель — 16, знаменатель — 5 правая квадратная скобка cup левая квадратная скобка дробь, числитель — 26, знаменатель — 5 ; дробь, числитель — 41, знаменатель — 5 правая квадратная скобка .

Задание 15 № 508355

Решите неравенство: дробь, числитель — 2x в степени 2 минус 2x плюс 1, знаменатель — 2x минус 1 меньше или равно 1.

Решение.

Преобразуем неравенство:

дробь, числитель — 2x в степени 2 минус 2x плюс 1 минус 2x плюс 1, знаменатель — 2x минус 1 меньше или равно 0 равносильно дробь, числитель — x в степени 2 минус 2x плюс 1, знаменатель — 2x минус 1 меньше или равно 0 равносильно дробь, числитель — (x минус 1) в степени 2 , знаменатель — 2x минус 1 меньше или равно 0.

Решения неравенства: x=1 или x меньше дробь, числитель — 1, знаменатель — 2 .

Ответ: левая круглая скобка минус принадлежит fty; дробь, числитель — 1, знаменатель — 2 правая круглая скобка cup{1}.

Задание 15 № 508360

Решите неравенство: дробь, числитель — 2x в степени 2 минус 6x, знаменатель — x минус 4 leq x.

Решение.

Решим неравенство методом интервалов:

дробь, числитель — 2x в степени 2 минус 6x, знаменатель — x минус 4 leq дробь, числитель — x в степени 2 минус 4x, знаменатель — x минус 4 равносильно дробь, числитель — x(x минус 2), знаменатель — x минус 4 leq0 равносильно совокупность выражений x меньше или равно 02 меньше или равно x меньше 4. конец совокупности .

Ответ: ( минус принадлежит fty;0>cup[2;4).

Задание 15 № 508364

Решите неравенство: дробь, числитель — (x минус 1) в степени 2 плюс 4(x плюс 1) в степени 2 , знаменатель — 2 меньше или равно дробь, числитель — (3x плюс 1) в степени 2 , знаменатель — 4 .

Решение.

Решим первое неравенство:

дробь, числитель — (x минус 1) в степени 2 плюс 4(x плюс 1) в степени 2 , знаменатель — 2 меньше или равно дробь, числитель — (3x плюс 1) в степени 2 , знаменатель — 4 равносильно 2(x минус 1) в степени 2 плюс 8(x плюс 1) в степени 2 меньше или равно (3x плюс 1) в степени 2 равносильно

равносильно 2x в степени 2 минус 4x плюс 2 плюс 8x в степени 2 плюс 16x плюс 8 меньше или равно 9x в степени 2 плюс 6x плюс 1 равносильно

равносильно x в степени 2 плюс 6x плюс 9 меньше или равно 0 равносильно (x плюс 3) в степени 2 меньше или равно 0 равносильно x= минус 3.

Ответ: { минус 3}.

Задание 15 № 508367

Решите неравенство: дробь, числитель — x в степени 2 минус 2x минус 2, знаменатель — x в степени 2 минус 2x плюс дробь, числитель — 7x минус 19, знаменатель — x минус 3 меньше или равно дробь, числитель — 8x плюс 1, знаменатель — x .

Решение.

Решим неравенство методом интервалов:

дробь, числитель — x в степени 2 минус 2x минус 2, знаменатель — x в степени 2 минус 2x плюс дробь, числитель — 7x минус 19, знаменатель — x минус 3 меньше или равно дробь, числитель — 8x плюс 1, знаменатель — x равносильно 1 минус дробь, числитель — 2, знаменатель — x в степени 2 минус 2x плюс 7 плюс дробь, числитель — 2, знаменатель — x минус 3 минус 8 минус дробь, числитель — 1, знаменатель — x le0 равносильно

равносильно минус дробь, числитель — 2, знаменатель — x в степени 2 минус 2x плюс дробь, числитель — 2, знаменатель — x минус 3 минус дробь, числитель — 1, знаменатель — x le0 равносильно минус дробь, числитель — 2, знаменатель — x левая круглая скобка x минус 2 правая круглая скобка плюс дробь, числитель — 2, знаменатель — x минус 3 минус дробь, числитель — 1, знаменатель — x le0 равносильно дробь, числитель — x(x минус 1), знаменатель — x левая круглая скобка x минус 3 правая круглая скобка левая круглая скобка x минус 2 правая круглая скобка le0 равносильно совокупность выражений новая строка x меньше 0, новая строка 0 меньше x меньше или равно 1, новая строка 2 меньше x меньше 3. конец совокупности .

Ответ: ( минус принадлежит fty;0)cup(0;1>cup(2;3).

Задание 15 № 508371

Решите неравенство: дробь, числитель — x в степени 4 минус 5x в степени 3 плюс 3x минус 25, знаменатель — x в степени 2 минус 5x больше или равно x в степени 2 минус дробь, числитель — 1, знаменатель — x минус 4 плюс дробь, числитель — 5, знаменатель — x .

Решение.

Решим неравенство методом интервалов:

дробь, числитель — x в степени 4 минус 5x в степени 3 плюс 3x минус 25, знаменатель — x в степени 2 минус 5x больше или равно x в степени 2 минус дробь, числитель — 1, знаменатель — x минус 4 плюс дробь, числитель — 5, знаменатель — x равносильно x в степени 2 плюс дробь, числитель — 3x минус 25, знаменатель — x(x минус 5) минус дробь, числитель — 5, знаменатель — x больше или равно x в степени 2 минус дробь, числитель — 1, знаменатель — x минус 4 равносильно

равносильно дробь, числитель — 3x минус 25 минус 5(x минус 5), знаменатель — x(x минус 5) плюс дробь, числитель — 1, знаменатель — x минус 4 больше или равно 0 равносильно дробь, числитель — минус 2x, знаменатель — x(x минус 5) плюс дробь, числитель — 1, знаменатель — x минус 4 больше или равно 0 равносильно

равносильно система выражений дробь, числитель — 1, знаменатель — x минус 4 минус дробь, числитель — 2, знаменатель — x минус 5 больше или равно 0,x не равно 0. конец системы равносильно система выражений дробь, числитель — x минус 5 минус 2(x минус 4), знаменатель — (x минус 4)(x минус 5) больше или равно 0,x не равно 0 конец системы равносильно

равносильно система выражений дробь, числитель — 3 минус x, знаменатель — (x минус 4)(x минус 5) больше или равно 0,x не равно 0. конец системы равносильно совокупность выражений x меньше 0, 0 меньше x меньше или равно 3, 4 меньше x меньше 5. конец совокупности

Ответ: ( минус принадлежит fty;0)cup(0;3>cup(4;5).

Задание 15 № 508381

Решите неравенство: x в степени 2 минус 3x плюс 1 минус дробь, числитель — x в степени 3 плюс x в степени 2 плюс 3x минус 21, знаменатель — x больше или равно 3.

Решение.

Решим второе неравенство:

дробь, числитель — x(x в степени 2 минус 3x плюс 1), знаменатель — x минус дробь, числитель — x в степени 3 плюс x в степени 2 плюс 3x минус 21, знаменатель — x больше или равно дробь, числитель — 3x, знаменатель — x равносильно дробь, числитель — минус 4x в степени 2 минус 5x плюс 21, знаменатель — x больше или равно 0 равносильно дробь, числитель — минус (x плюс 3)(4x минус 7), знаменатель — x больше или равно 0 равносильно

равносильно дробь, числитель — (x плюс 3)(4x минус 7), знаменатель — x меньше или равно 0 равносильно совокупность выражений новая строка x меньше или равно минус 3, новая строка 0 меньше x меньше или равно дробь, числитель — 7, знаменатель — 4 . конец совокупности

Ответ: ( минус принадлежит fty; минус 3>cup левая круглая скобка 0; дробь, числитель — 7, знаменатель — 4 правая квадратная скобка .

Задание 15 № 508429

Решите неравенство: левая круглая скобка дробь, числитель — 2, знаменатель — 25x в степени 2 минус 10x минус 8 плюс дробь, числитель — 25x в степени 2 минус 10x минус 8, знаменатель — 2 правая круглая скобка в степени 2 больше или равно 4.

Решение.

Сделав замену t= дробь, числитель — 25x в степени 2 минус 10x минус 8, знаменатель — 2 , получаем:

левая круглая скобка дробь, числитель — 1, знаменатель — t плюс t правая круглая скобка в степени 2 больше или равно 4 равносильно дробь, числитель — 1, знаменатель — t в степени 2 плюс 2 плюс t в степени 2 ge4 равносильно дробь, числитель — 1, знаменатель — t в степени 2 минус 2 плюс t в степени 2 ge0 равносильно левая круглая скобка дробь, числитель — 1, знаменатель — t минус t правая круглая скобка в степени 2 больше или равно 0 равносильно t не равно 0.

Значит, x не равно минус дробь, числитель — 2, знаменатель — 5 и x не равно дробь, числитель — 4, знаменатель — 5 .

Ответ: левая круглая скобка минус принадлежит fty; минус дробь, числитель — 2, знаменатель — 5 правая круглая скобка cup левая круглая скобка минус дробь, числитель — 2, знаменатель — 5 ; дробь, числитель — 4, знаменатель — 5 правая круглая скобка cup левая круглая скобка дробь, числитель — 4, знаменатель — 5 ; плюс принадлежит fty правая круглая скобка .

Задание 15 № 508432

Решите неравенство: { дробь, числитель — x в степени 5 минус x в степени 2 , знаменатель — x в степени 2 больше или равно дробь, числитель — x в степени 3 минус 1, знаменатель — 4x в степени 2 }.

Решение.

Решим неравенство методом интервалов:

дробь, числитель — x в степени 5 минус x в степени 2 , знаменатель — x в степени 2 больше или равно дробь, числитель — x в степени 3 минус 1, знаменатель — 4x в степени 2 равносильно дробь, числитель — (x в степени 3 минус 1)(4x в степени 2 минус 1), знаменатель — x в степени 2 больше или равно 0 равносильно дробь, числитель — (x минус 1)(2x минус 1)(2x плюс 1), знаменатель — x в степени 2 больше или равно 0 равносильно совокупность выражений новая строка минус 0,5 меньше или равно x меньше 0, новая строка 0 меньше x меньше или равно 0,5, новая строка x больше или равно 1. конец совокупности .

Ответ:

[ минус 0,5;0)cup(0;0,5>cup[1; плюс принадлежит fty).

Задание 15 № 508434

Решите неравенство: {4 умножить на дробь, числитель — x в степени 3 плюс x в степени 2 , знаменатель — x в степени 2 минус 2x плюс 1 меньше или равно 9 умножить на дробь, числитель — x плюс 1, знаменатель — x в степени 2 минус 2x плюс 1 }.

Решение.

Решим неравенство методом интервалов:

4 умножить на дробь, числитель — x в степени 3 плюс x в степени 2 , знаменатель — x в степени 2 минус 2x плюс 1 меньше или равно 9 умножить на дробь, числитель — x плюс 1, знаменатель — x в степени 2 минус 2x плюс 1 равносильно дробь, числитель — 4x в степени 3 плюс 4x в степени 2 минус 9x минус 9, знаменатель — (x минус 1) в степени 2 меньше или равно 0 равносильно дробь, числитель — (x плюс 1)(2x минус 3)(2x плюс 3), знаменатель — (x минус 1) в степени 2 меньше или равно 0 равносильно совокупность выражений новая строка x меньше или равно минус дробь, числитель — 3, знаменатель — 2 , новая строка минус 1 меньше или равно x меньше 1, новая строка 1 меньше x меньше или равно дробь, числитель — 3, знаменатель — 2 . конец совокупности .

Ответ: 

левая круглая скобка минус принадлежит fty; минус дробь, числитель — 3, знаменатель — 2 правая квадратная скобка cup[ минус 1;1)cup левая круглая скобка 1; дробь, числитель — 3, знаменатель — 2 правая квадратная скобка .

Задание 15 № 508442

Решите неравенство: x в степени 2 плюс (2 минус корень из { 15})x минус 2 корень из { 15} меньше или равно 0.

Решение.

По теореме Виета, сумма корней уравнения равна минус 2 плюс корень из { 15}, а их произведение равно минус 2 корень из { 15}. Поэтому корни этого уравнения — числа минус 2 и корень из { 15}. Тогда неравенство можно решить так:

x в степени 2 плюс (2 минус корень из { 15})x минус 2 корень из { 15} меньше или равно 0 равносильно (x плюс 2)(x минус корень из { 15}) меньше или равно 0 равносильно минус 2 меньше или равно x меньше или равно корень из { 15}.

Ответ: [ минус 2; корень из { 15}>.

Задание 15 № 508447

Решите неравенство: x корень из { 8} минус 7x плюс 14 корень из { 8} больше 57.

Решение.

Преобразуем неравенство:

x корень из { 8} минус 7x плюс 14 корень из { 8} больше 57 равносильно ( корень из { 8} минус 7)x плюс 14 корень из { 8} минус 57 больше 0 равносильно x меньше дробь, числитель — 57 минус 14 корень из { 8}, знаменатель — корень из { 8 минус 7} равносильно x меньше дробь, числитель — ( корень из { 8} минус 7) в степени 2 , знаменатель — корень из { 8 минус 7} равносильно x меньше корень из { 8} минус 7.

Ответ: левая круглая скобка минус принадлежит fty; корень из { 8} минус 7 правая круглая скобка .

Задание 15 № 508449

Решите неравенство: (10x плюс 7)(4 минус 5x) левая круглая скобка 50x в степени 2 минус 5x минус 28 правая круглая скобка меньше 0.

Решение.

Заметим, что (10x плюс 7)(4 минус 5x)(50x в степени 2 минус 5x минус 28)= минус (10x плюс 7)(5x минус 4)(10x плюс 7)(5x минус 4)= минус (10x плюс 7) в степени 2 (4 минус 5x) в степени 2 , поэтому неравенство минус (10x плюс 7) в степени 2 (4 минус 5x) в степени 2 меньше 0 выполнено при всех x, кроме x= минус 0,7 и x=0,8.

Ответ: ( минус принадлежит fty; минус 0,7)cup( минус 0,7;0,8)cup(0,8; плюс принадлежит fty).

Задание 15 № 508530

Решите неравенство: 2x плюс 1 минус дробь, числитель — 21x плюс 39 , знаменатель — x в степени 2 плюс x минус 2 больше или равно минус дробь, числитель — 1, знаменатель — x плюс 2 .

Решение.

Последовательно получаем:

2x плюс 1 минус дробь, числитель — 21x плюс 39 , знаменатель — x в степени 2 плюс x минус 2 больше или равно минус дробь, числитель — 1, знаменатель — x плюс 2 равносильно 2x плюс 1 минус дробь, числитель — 20(x плюс 2), знаменатель — (x плюс 2)(x минус 1) минус дробь, числитель — x минус 1, знаменатель — (x плюс 2)(x минус 1) больше или равно минус дробь, числитель — 1, знаменатель — x плюс 2 равносильно

равносильно система выражений новая строка 2x плюс 1 минус дробь, числитель — 20, знаменатель — x минус 1 больше или равно 0, новая строка x не равно минус 2 конец системы . равносильно система выражений новая строка дробь, числитель — (x плюс 3)(2x минус 7), знаменатель — x минус 1 больше или равно 0, новая строка x не равно минус 2 конец системы . равносильно совокупность выражений новая строка минус 3 меньше или равно x меньше минус 2, новая строка минус 2 меньше x меньше 1, новая строка x больше или равно дробь, числитель — 7, знаменатель — 2 . конец совокупности .

Ответ:

[ минус 3; минус 2)cup( минус 2;1)cup левая квадратная скобка дробь, числитель — 7, знаменатель — 2 ; плюс принадлежит fty правая круглая скобка .

Задание 15 № 512484

Решите неравенство дробь, числитель — x, знаменатель — x в степени 2 плюс 3 меньше или равно дробь, числитель — 1, знаменатель — 4 x в степени минус 1 .

Решение.

Преобразуем неравенство:

дробь, числитель — x, знаменатель — x в степени 2 плюс 3 меньше или равно дробь, числитель — 1, знаменатель — 4x равносильно дробь, числитель — 4x в степени 2 минус x в степени 2 минус 3, знаменатель — (x в степени 2 плюс 3)4x le0 равносильно дробь, числитель — (x минус 1)(x плюс 1), знаменатель — (x в степени 2 плюс 3)x le0.

Учитывая, что при всех значениях x выражение x2 + 3 положительно, получаем

дробь, числитель — (x минус 1)(x плюс 1), знаменатель — x le0,

откуда

xle минус 1,0 меньше xle1.

Ответ: ( минус принадлежит fty; минус 1>cup (0;1].

Задание 15 № 507203

Решите неравенство дробь, числитель — 2 минус (x минус 6) в степени минус 1 , знаменатель — 5(x минус 6) в степени минус 1 минус 1 меньше или равно минус 0,2.

Решение.

Сделаем замену y= дробь, числитель — 1, знаменатель — { x минус 6}. Получим

дробь, числитель — 2 минус y, знаменатель — 5y минус 1 меньше или равно минус 0,2 равносильно дробь, числитель — 1,8, знаменатель — 5y минус 1 le0 равносильно y меньше дробь, числитель — 1, знаменатель — 5 .

Следовательно, дробь, числитель — 1, знаменатель — { x минус 6} меньше дробь, числитель — 1, знаменатель — 5 равносильно дробь, числитель — 11 минус x, знаменатель — x минус 6 меньше 0 равносильно совокупность выражений новая строка x меньше 6, новая строка x больше 11. конец совокупности .

Ответ: ( минус принадлежит fty;6)cup (11; плюс принадлежит fty)

Задание 15 № 515707

Решите неравенство x плюс дробь, числитель — 20, знаменатель — x плюс 6 ge6.

Решение.

Решим неравенство:

x плюс дробь, числитель — 20, знаменатель — x плюс 6 ge6 равносильно x плюс дробь, числитель — 20 минус 6x минус 36, знаменатель — x плюс 6 больше или равно 0 равносильно x минус дробь, числитель — 6x плюс 16, знаменатель — x плюс 6 больше или равно 0 равносильно дробь, числитель — x в степени 2 минус 16, знаменатель — x плюс 6 больше или равно 0 равносильно дробь, числитель — (x плюс 4)(x минус 4), знаменатель — x плюс 6 больше или равно 0 равносильно совокупность выражений система выражений x больше минус 6,xle4, конец системы . xge4. конец совокупности .

Ответ: ( минус 6; минус 4> cup [4; плюс принадлежит fty).

Задание 15 № 516402

Решите неравенство дробь, числитель — 4x в степени 4 минус 4x в степени 3 плюс x в степени 2 , знаменатель — минус 2x в степени 2 плюс 5x минус 2 плюс дробь, числитель — 2x в степени 3 минус 7x в степени 2 плюс 5x плюс 1, знаменатель — x минус 2 меньше или равно 0.

Решение.

Преобразуем неравенство:

дробь, числитель — 4x в степени 4 минус 4x в степени 3 плюс x в степени 2 , знаменатель — минус 2x в степени 2 плюс 5x минус 2 плюс дробь, числитель — 2x в степени 3 минус 7x в степени 2 плюс 5x плюс 1, знаменатель — x минус 2 меньше или равно 0 равносильно дробь, числитель — x в степени 2 (2x минус 1) в степени 2 , знаменатель — (2x минус 1)(2 минус x) плюс дробь, числитель — 2x в степени 3 минус 7x в степени 2 плюс 5x плюс 1, знаменатель — x минус 2 меньше или равно 0 равносильно

равносильно система выражений дробь, числитель — минус 6x в степени 2 плюс 5x плюс 1, знаменатель — x минус 2 меньше или равно 0, x не равно дробь, числитель — 1, знаменатель — 2 конец системы . равносильно система выражений дробь, числитель — (6x плюс 1)(x минус 1), знаменатель — x минус 2 больше или равно 0, x не равно дробь, числитель — 1, знаменатель — 2 конец системы . равносильно совокупность выражений минус дробь, числитель — 1, знаменатель — 6 меньше или равно x меньше дробь, числитель — 1, знаменатель — 2 , дробь, числитель — 1, знаменатель — 2 меньше xle1, x больше 2. конец совокупности .

Ответ: x принадлежит левая квадратная скобка минус дробь, числитель — 1, знаменатель — 6 ; дробь, числитель — 1, знаменатель — 2 правая круглая скобка cup левая круглая скобка дробь, числитель — 1, знаменатель — 2 ;1 правая квадратная скобка cup (2; плюс принадлежит fty).

Задание 15 № 521996

Решите неравенство x в степени 3 плюс 2x в степени 2 минус дробь, числитель — 24x в степени 2 минус x плюс 3, знаменатель — x минус 3 le1.

Решение.

Решим неравенство методом интервалов:

дробь, числитель — левая круглая скобка x в степени 3 плюс 2x в степени 2 правая круглая скобка (x минус 3) минус 24x в степени 2 плюс x минус 3, знаменатель — x минус 3 меньше или равно 1 равносильно дробь, числитель — x в степени 4 плюс 2x в степени 3 минус 3x в степени 3 минус 6x в степени 2 минус 24x в степени 2 плюс x минус 3 минус x плюс 3, знаменатель — x минус 3 меньше или равно 0 равносильно дробь, числитель — x в степени 4 минус x в степени 3 минус 30x в степени 2 , знаменатель — x минус 3 меньше или равно 0 равносильно

равносильно дробь, числитель — x в степени 2 (x минус 6)(x плюс 5), знаменатель — x минус 3 меньше или равно 0,

откуда xle минус 5, x=0 и 3 меньше xle6.

Ответ: ( минус принадлежит fty; минус 5>;{0}; (3;6].

Задание 15 № 522124

Решите неравенство x в степени 3 плюс 5x в степени 2 плюс дробь, числитель — 30x в степени 2 плюс x минус 8, знаменатель — x минус 8 le1.

Решение.

Решим неравенство методом интервалов:

дробь, числитель — (x в степени 3 плюс 5x в степени 2 )(x минус 8) плюс 30x в степени 2 плюс x минус 8, знаменатель — x минус 8 le1 равносильно дробь, числитель — x в степени 4 плюс 5x в степени 3 минус 8x в степени 3 минус 40x в степени 2 плюс 30x в степени 2 плюс x минус 8 минус x плюс 8, знаменатель — x минус 8 le0 равносильно дробь, числитель — x в степени 4 минус 3x в степени 3 минус 10x в степени 2 , знаменатель — x минус 8 le0 равносильно

равносильно дробь, числитель — x в степени 2 (x минус 5)(x плюс 2), знаменатель — x минус 8 le0,

откуда xle минус 2,x=0 и 5 меньше или равно x меньше 8.

Ответ: ( минус принадлежит fty; минус 2>cup{0}cup[5; 8).

Задание 15 № 523996

Решите неравенство дробь, числитель — x в степени 2 минус 3x минус 2, знаменатель — x в степени 2 минус 3x плюс 2 плюс дробь, числитель — x в степени 2 минус 3x плюс 16, знаменатель — x в степени 2 минус 3x ge0.

Решение.

Сделаем замену y=x в степени 2 минус 3x. Получим:

дробь, числитель — y минус 2, знаменатель — y плюс 2 плюс дробь, числитель — y плюс 16, знаменатель — y ge0 равносильно дробь, числитель — y в степени 2 минус 2y плюс y в степени 2 плюс 18y плюс 32, знаменатель — y(y плюс 2) ge0 равносильно дробь, числитель — 2y в степени 2 плюс 16y плюс 32, знаменатель — y(y плюс 2) ge0 равносильно дробь, числитель — 2(y плюс 4) в степени 2 , знаменатель — y(y плюс 2) ge0 равносильно совокупность выражений y меньше минус 2,y больше 0. конец совокупности .

Отсюда после обратной замены получаем:

совокупность выражений x в степени 2 минус 3x меньше минус 2,x в степени 2 минус 3x больше 0 конец совокупности . равносильно совокупность выражений x в степени 2 минус 3x плюс 2 меньше 0,x(x минус 3) больше 0 конец совокупности . равносильно совокупность выражений 1 меньше x меньше 2,x меньше 0,x больше 3. конец совокупности .

Ответ: ( минус принадлежит fty;0)cup(1;2)cup(3; плюс принадлежит fty).

Задание 15 № 526726

Решите неравенство x плюс 1 минус дробь, числитель — 4, знаменатель — x плюс 1 больше или равно дробь, числитель — 6 минус 4 x минус 2 x в степени 2 , знаменатель — x плюс 2 .

Решение.

Преобразуем неравенство:

дробь, числитель — (x плюс 1) в степени 2 минус 4, знаменатель — x плюс 1 больше или равно дробь, числитель — минус 2(x минус 1)(x плюс 3), знаменатель — x плюс 2 равносильно дробь, числитель — (x минус 1)(x плюс 3), знаменатель — x плюс 1 плюс дробь, числитель — 2(x минус 1)(x плюс 3), знаменатель — x плюс 2 больше или равно 0 равносильно

равносильно дробь, числитель — (x минус 1)(x плюс 3)(x плюс 2 плюс 2(x плюс 1)), знаменатель — (x плюс 1)(x плюс 2) больше или равно 0 равносильно дробь, числитель — (x минус 1)(x плюс 3)(3x плюс 4), знаменатель — (x плюс 1)(x плюс 2) больше или равно 0.

Решая полученное неравенство методом интервалов (см. рис.), находим ответ: минус 3 меньше или равно x меньше минус 2; минус дробь, числитель — 4, знаменатель — 3 меньше или равно x меньше минус 1; x больше или равно 1.

Ответ: [ минус 3; минус 2)cup левая квадратная скобка минус дробь, числитель — 4, знаменатель — 3 ; минус 1 правая круглая скобка cup [1; плюс принадлежит fty).

Задание 15 № 530384

Решите неравенство: дробь, числитель — 1, знаменатель — x(x плюс 1) плюс дробь, числитель — 1, знаменатель — (x плюс 1)(x плюс 2) плюс дробь, числитель — 1, знаменатель — (x плюс 2)(x плюс 3) меньше или равно дробь, числитель — 3, знаменатель — 4 .

Решение.

Заметим, что дробь, числитель — 1, знаменатель — n(n плюс 1) = дробь, числитель — 1, знаменатель — n минус дробь, числитель — 1, знаменатель — n плюс 1 . Применим эту формулу к каждому слагаемому левой части, получим:

дробь, числитель — 1, знаменатель — x минус дробь, числитель — 1, знаменатель — x плюс 1 плюс дробь, числитель — 1, знаменатель — x плюс 1 минус дробь, числитель — 1, знаменатель — x плюс 2 плюс дробь, числитель — 1, знаменатель — x плюс 2 минус дробь, числитель — 1, знаменатель — x плюс 3 меньше или равно дробь, числитель — 3, знаменатель — 4 равносильно

равносильно система выражений дробь, числитель — 1, знаменатель — x минус дробь, числитель — 1, знаменатель — x плюс 3 меньше или равно дробь, числитель — 3, знаменатель — 4 ,x не равно минус 1,x не равно минус 2 конец системы . равносильно система выражений дробь, числитель — 3, знаменатель — x(x плюс 3) меньше или равно дробь, числитель — 3, знаменатель — 4 ,x не равно минус 1,x не равно минус 2 конец системы . равносильно система выражений дробь, числитель — 1, знаменатель — x(x плюс 3) минус дробь, числитель — 1, знаменатель — 4 le0,x не равно минус 1,x не равно минус 2 конец системы . равносильно

равносильно система выражений дробь, числитель — 4 минус 3x минус x в степени 2 , знаменатель — x(x плюс 3) le0,x не равно минус 1,x не равно минус 2 конец системы . равносильно система выражений дробь, числитель — (x минус 1)(x плюс 4), знаменатель — x(x плюс 3) ge0,x не равно минус 1,x не равно минус 2 конец системы . равносильно совокупность выражений xle минус 4, минус 3 меньше x меньше минус 2, минус 2 меньше x меньше минус 1, минус 1 меньше x меньше 0,xge1. конец совокупности .

Ответ: ( минус принадлежит fty; минус 4>cup( минус 3; минус 2)cup( минус 2; минус 1)cup( минус 1;0)cup[1; плюс принадлежит fty).

Задание 15 № 530457

Решите неравенство дробь, числитель — x в степени 4 минус 2x в степени 3 плюс x в степени 2 , знаменатель — x в степени 2 плюс x минус 2 минус дробь, числитель — 2x в степени 3 плюс x в степени 2 плюс x минус 1, знаменатель — x плюс 2 le1.

Решение.

Запишем исходное неравенство в виде:

дробь, числитель — x в степени 4 минус 2x в степени 3 плюс x в степени 2 , знаменатель — x в степени 2 плюс x минус 2 минус дробь, числитель — 2x в степени 3 плюс x в степени 2 плюс x минус 1, знаменатель — x плюс 2 le1 равносильно дробь, числитель — x в степени 2 (x минус 1) в степени 2 , знаменатель — (x плюс 2)(x минус 1) минус дробь, числитель — 2x в степени 3 плюс x в степени 2 плюс 2x плюс 1, знаменатель — x плюс 2 le0 равносильно

равносильно система выражений дробь, числитель — минус x в степени 3 минус 2x в степени 2 минус 2x минус 1, знаменатель — x плюс 2 le0,x минус 1 не равно 0 конец системы . равносильно система выражений дробь, числитель — (x плюс 1)(x в степени 2 плюс x плюс 1), знаменатель — x плюс 2 ge0,x не равно 1 конец системы . равносильно совокупность выражений x меньше минус 2, минус 1 меньше или равно x меньше 1,x больше 1. конец совокупности .

Ответ: ( минус принадлежит fty; минус 2)cup[ минус 1;1)cup(1; плюс принадлежит fty).

Задание 15 № 530674

Решите неравенство дробь, числитель — 3, знаменатель — x в степени 2 плюс 13x плюс 40 больше или равно дробь, числитель — 1, знаменатель — x в степени 2 плюс 15x плюс 56 .

Решение.

Запишем исходное неравенство в виде:

дробь, числитель — 3, знаменатель — (x плюс 5)(x плюс 8) минус дробь, числитель — 1, знаменатель — (x плюс 7)(x плюс 8) ge0 равносильно дробь, числитель — 3(x плюс 7) минус (x плюс 5), знаменатель — (x плюс 5)(x плюс 7)(x плюс 8) ge0 равносильно

равносильно дробь, числитель — 2x плюс 16, знаменатель — (x плюс 5)(x плюс 7)(x плюс 8) ge0 равносильно система выражений дробь, числитель — 2, знаменатель — (x плюс 5)(x плюс 7) ge0,x не равно минус 8 конец системы . равносильно совокупность выражений x меньше минус 8, минус 8 меньше x меньше минус 7,x больше минус 5. конец совокупности .

Ответ: левая круглая скобка минус принадлежит fty; минус 8 правая круглая скобка cup левая круглая скобка минус 8; минус 7 правая круглая скобка cup( минус 5; плюс принадлежит fty).

Задание 15 № 530701

Решите неравенство: дробь, числитель — x, знаменатель — (x минус 2) в степени 3 плюс (x минус 3) в степени 3 минус 1 ge0.

Решение.

Разложим разность (x минус 2) в степени 3 минус 1 по формуле разности кубов, получим:

(x минус 2) в степени 3 минус 1 = (x минус 2 минус 1)((x минус 2) в степени 2 плюс (x минус 2) плюс 1) = (x минус 3)(x в степени 2 минус 3x плюс 3).

Вынесем в знаменателе общий множитель за скобки:

дробь, числитель — x, знаменатель — (x минус 3)(x в степени 2 минус 3x плюс 3) плюс (x минус 3) в степени 3 ge0 равносильно дробь, числитель — x, знаменатель — (x минус 3)(x в степени 2 минус 3x плюс 3 плюс x в степени 2 минус 6x плюс 9) ge0 равносильно

равносильно дробь, числитель — x, знаменатель — (x минус 3)(2x в степени 2 минус 9x плюс 12) ge0 равносильно дробь, числитель — x, знаменатель — x минус 3 ge0 равносильно совокупность выражений x больше 3,xle0. конец совокупности .

Ответ: ( минус принадлежит fty;0>cup (3; плюс принадлежит fty).

Источник

Задания

Версия для печати и копирования в MS Word

Задания Д4 № 27888

Найдите величину угла ABC. Ответ дайте в градусах.

Спрятать решение

Решение.

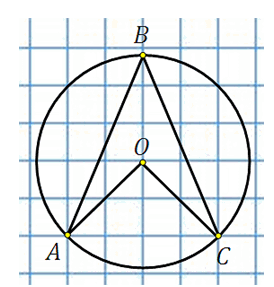
Центральный угол, опирающийся на хорду АС равен 90°, поэтому меньшая дуга окружности, отсекаемая этой хордой, также равна 90°, а большая  — равна 270°. Опирающийся на нее вписанный угол ABC равен ее половине т. е. 135°.

Ответ: 135.

Аналоги к заданию № 27887: 27888 27889 26234 26235 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.1.4 Окружность и круг, 5.1.5 Вписанная и описанная окружность треугольника, 5.5.1 Величина угла, градусная мера угла

Спрятать решение

·

Прототип задания

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

  • ЗАДАЧИ ЕГЭ С ОТВЕТАМИ

  • АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-13

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

  • РубрикиРубрики
  • Задачи по номерам!

    №1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16

  • МЕТКИ

    БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие

  • ОСТЕОХОНДРОЗУ-НЕТ!

Тема 25.

Программирование — Обработка целочисленной информации

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

программирование — обработка целочисленной информации

25.01Маска числа

25.02Поиск делителей

25.03Числа-палиндромы

25.04Простые числа

25.05Прочие прототипы

Решаем задачу:

Пусть M — сумма минимального и максимального натурального делителей целого числа, не считая единицы и самого числа.
Если таких делителей нет, то считаем значение M равным нулю.

Напишите программу, которая перебирает целые числа, большие 452 021, в порядке возрастания и ищет среди них
такие, для которых значение М при делении на 7 дает в остатке 3. Вывести первые 5 найденных чисел и соответствующие
им значения М.

Показать ответ и решение

def m(n):

     for i in range(2, int(n ** 0.5) + 1):

         if n % i == 0:

             return i + n // i

     return 0

 k = 0

 for i in range(452021 + 1, 10000000000000):

     if m(i) % 7 == 3:

         print(i, m(i))

         k += 1

     if k == 5: break

Ответ:

452025 150678 452029 23810 452034 226019 452048 226026 452062 226033

Дата: 2016-01-26

21416

Категория: Вписанный угол

Метка: ЕГЭ-№1ОкружностьУглы

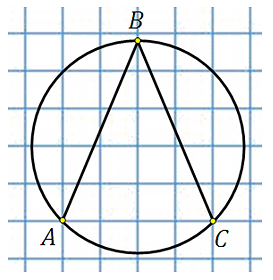
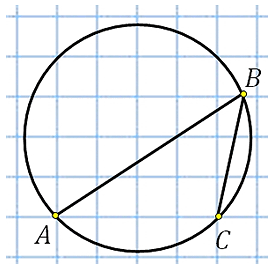
27887. Найдите величину угла ABC. Ответ дайте в градусах.

1

Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:

2

Угол АОС равен 900. Это видно по тому как проходят АО и ОС относительно клетчатой сетки. Угол АВС это вписанный угол, построенный на той же дуге.

По свойству вписанного угла:

3

Ответ: 45

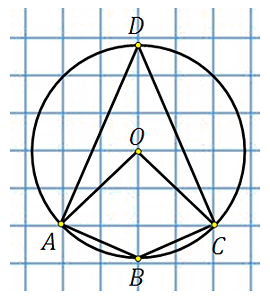
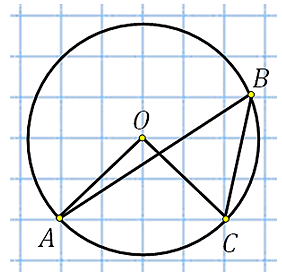
27888. Найдите величину угла ABC. Ответ дайте в градусах.

1

Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС и вписанный угол ADC:

2

Центральный угол АОС равен 900. По свойству вписанного угла

3

Известно, что у четырёхугольника вписанного в окружность сумма противоположных углов равна 180 градусам, следовательно:

4

Ответ: 135

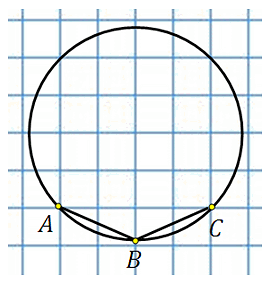
27889. Найдите величину угла ABC. Ответ дайте в градусах.

1

Отметим центр окружности (видно о клетчатой сетке). Обозначим его точкой О, построим центральный угол АОС:

2

Угол АОС равен 90 градусов. Угол АВС это вписанный угол, построенный на той же дуге. По свойству вписанного угла:

3

Ответ: 45

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Ok

Жуки (2019)

WEB-DL

  • Год выхода: 2019
  • Страна: Россия
  • Жанр: Комедия
  • Режиссер: Константин Смирнов, Константин Колесов
  • Актёры: Вячеслав Чепурченко, Павел Комаров, Вадим Дубровин, Максим Лагашкин, Екатерина Стулова
  • Сезоны: 1-3 сезон
  • Серии: 1-16 серия
  • Время: 00:30

Никита, Дэн и Артемий разработали уникальное приложение для смартфонов, вот-вот продадут его и осуществят все свои мечты. Но в последний момент многомиллионная сделка срывается и парней забирают в армию. Чтобы не ставить под угрозу успех своего стартапа, они выбирают альтернативную службу в глухой деревне Жуки, где будут пытаться довести свой проект до конца. Только не так просто разрабатывать приложение там, где нет даже интернета…

Смотреть онлайн Жуки (2019) в хорошем качестве HD

Плеер 1
Плеер 2

В закладки

Решение 18 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023

Скачать сборник в pdf

Угол между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C треугольника ABC, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

картинка

Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.

картинка

Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шашистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шашистом из России.

Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.

Найдите корень уравнения (log_4{2^{5x+7}}=3).

Найдите значение выражения (dfrac{a^{3{,}33}}{a^{2{,}11}cdot a^{2{,}22}}) при (a=dfrac{2}{7}).

Прямая (y=9x+6) является касательной к графику (y=ax^2-19x+13). Найдите (a).

Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400) км − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?

Первый садовый насос перекачивает 10 литров воды за 5 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литров воды?

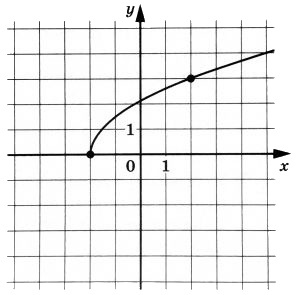
На рисунке изображен график функции (f(x)=ksqrt{x+p}). Найдите (f(0{,}25)).

картинка

Найдите наибольшее значение функции (y=2x^2-12x+8ln{x}-5) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right]).

а) Решите уравнение (7cos{x}-4cos^3{x}=2sqrt{3}sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-4pi;-3piright])

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.

а)

1. 2πn, n∈Z 2. π/6+2πn, n∈Z 3. π/4+2πn, n∈Z 4. π/3+2πn, n∈Z
5. π/2+2πn, n∈Z 6. 2π/3+2πn, n∈Z 7. 3π/4+2πn, n∈Z 8. 5π/6+2πn, n∈Z
9. π+2πn, n∈Z 10. -π/6+2πn, n∈Z 11. -π/4+2πn, n∈Z 12. -π/3+2πn, n∈Z
13. -π/2+2πn, n∈Z 14. -2π/3+2πn, n∈Z 15. -3π/4+2πn, n∈Z 16. -5π/6+2πn, n∈Z

б)

17. -4π 18. -23π/6 19. -15π/4 20. -11π/3
21. -7π/2 22. -10π/3 23. -13π/4 24. -19π/6
25. -3π      

Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=2AC.

Решите неравенство (log^2_{5}{left(x^4right)}-28log_{0{,}04}{left(x^2right)}leqslant 8).

Производство (x) тыс. единиц продуктции обходится в (q=3x^2+6x+13) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении (x)?

Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB=AC=17 и BC=16. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.

Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-a+3right)^2+left(y+a-2right)^2=a+dfrac{7}{2},  x-y=a-1 end{cases})имеет единственное решение.

Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{5}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{8}right]+left[dfrac{n}{23}right]=n+2021)?

Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.

Скачать тренировочный вариант и ответы

Посмотреть другие тренировочные варианты

variant_26_oge2023_matematika_9klass

Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.

Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.

1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.

Ответ: 1432

2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?

Ответ: 25

3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?

Ответ: 105

4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.

Ответ: 17

5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.

Ответ: 100

6. Найдите значение выражения 4,4 − 1,7.

Ответ: 2,7

8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.

Ответ: 16

9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 8) 2 .

Ответ: 6, 5

10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.

Ответ: 0, 75

11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.

Ответ: 312

12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?

Ответ: 176

13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.

Ответ: 1

14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?

Ответ: 8

15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.

Ответ: 10

16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.

Ответ: 64

17. Найдите площадь квадрата, описанного около окружности радиуса 40.

Ответ: 6400

18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.

Ответ: 4

19. Какое из следующих утверждений верно?

1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

Ответ: 2

20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).

Ответ: -2; -1; 1

21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?

Ответ: 22

23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.

Ответ: 12

24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.

25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.

Ответ: 820

Тренировочные варианты ОГЭ по математике 9 класс задания с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Шкалирование

Первичный Тестовый Оценка
5-6 27-34 3
7-8 40-46 4
9-10 52-58
11-12-13 64-66-68 5
14-15-16 70-72-74
17-18-19 76-78-80
20-21-22 82-84-86
23-24-25 88-90-92
26-27-28 94-96-98
29-30-31 100
Первичный балл
/
Тестовый балл		 5/27 6/34 7/40 8/46 9/52 10/58 11/64 12/66 13/68 14/70
15/72 16/74 17/76 18/78 19/80 20/82 X / 2X+42 29+ / 100
Источник

Натуральное рациональное
шестизначное
нечетное
число 508213
является простым числом.

19 — сумма цифр данного числа.
Делители числа 508213: 1, 508213.

508213 и 0.0000019676789062853567 — это обратные числа.

Данное число можно представить произведением: 1 * 508213.

Перевод числа 508213 в другие системы счисления:
двоичная система счисления: 1111100000100110101, троичная система счисления: 221211010201, восьмеричная система счисления: 1740465, шестнадцатеричная система счисления: 7C135.
В числе 508213 496 килобайтов 309 байтов .

Число азбукой Морзе: ….. —— —.. ..— .—- …—

Косинус: -0.7661, синус: -0.6427, тангенс: 0.8389.
У числа есть натуральный логарифм: 13.1387.
Логарифм десятичный числа: 5.7060.
712.8906 это квадратный корень из числа, 79.8023 — кубический.
Возведение числа 508213 в квадрат: 2.5828e+11.

Число секунд 508213 можно представить как 5 дней 21 час 10 минут 13 секунд .
Нумерологическая цифра этого числа — 1.

Источник

ЕГЭ по биологии 11 класс 2023. Тренировочный вариант (задания и ответы)ЕГЭ 2023. Экзаменационная работа состоит из двух частей, включающих в себя 29 заданий. Часть 1 содержит 22 задания с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом. На выполнение экзаменационной работы по биологии отводится 3 часа 55 минут (235 минут).

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки. Ответами к заданиям 1–22 являются последовательность цифр, число или слово (словосочетание). Ответы запишите в поля ответов в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ № 1 справа от номеров соответствующих заданий, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.

Скачать тренировочный вариант ЕГЭ: Скачать

Скачать ответы на тренировочный вариант ЕГЭ: Скачать

Задания:

1. Рассмотрите таблицу «Методы биологических исследований» и заполните ячейку, вписав соответствующий термин. Применяется для выявления геномных мутаций.

2. Исследователь добавлял в стакан коровьего молока желудочный сок собаки. Как спустя час в стакане изменится содержание дисахарида лактозы и животных жиров? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась

3. Площадь земель, покрытых лесом, в России составляет примерно 1200 млн га. Известно, что 12 га леса связывают 18 тонн диоксида углерода в год. Сколько млн тонн углекислого газа может быть связано за год за счет российских лесов?

4. Определите вероятность (в %) гибели от анемии ребенка, родившегося в браке гомозиготных по рецессивному аллелю родителей, если эта форма анемии наследуется как аутосомный доминантный признак. В ответ запишите только соответствующее число.

5. Каким номером на рисунке обозначена структура, образующая спираль в сперматозоидах млекопитающих?

6. Установите соответствие между характеристиками и структурами, обозначенными на рисунке цифрами 1, 2, 3, 4: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.

7. Выберите три признака, которые соответствуют описаниям селекции. Запишите в таблицу цифры, под которыми они указаны.
1) выведение новых штаммов микроорганизмов
2) получение новых семейств растений
3) получение генномодифицированных растений
4) выведение тритикале при скрещивании пшеницы и ржи
5) получение рекомбинантной плазмиды
6) выведение пород животных и сортов растений

8. Установите последовательность этапов ферментативного катализа. Запишите в таблицу соответствующую последовательность цифр.
1) образование нестабильного комплекса фермент-продукт
2) сближение фермента и субстрата
3) начало распада комплекса фермент-продукт
4) формирование фермент-субстратного комплекса
5) высвобождение продукта и фермента
9. Какой цифрой на рисунке обозначена вторичная полость тела?

10. Установите соответствие между характеристиками и структурами тела дождевого червя, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.

11. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Для растения, изображенного на рисунке, характерно:
1) гаметофит обоеполый — содержит архегонии и антеридии
2) дихотомическое ветвление
3) заросток сердцевидной формы
4) споры созревают в сорусах
5) споры образуются в спороносных колосках
6) гаметофит формирует вайи

12. Установите последовательность систематических групп, начиная с самого низкого ранга. Запишите в таблицу соответствующую последовательность цифр.
1) Эукариоты
2) Членистоногие
3) Ежемухи
4) Ежемуха свирепая
5) Двукрылые
6) Животные

13. Какой цифрой на рисунке указан тип научения, который изучал К. Лоренц?

14. Установите соответствие между характеристиками и типами научения, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.

15. Выберите три верно обозначенные подписи к рисунку «Строение уха». Запишите цифры, под которыми они указаны.
1) серная (церуминозная) железа
2) наружный слуховой проход
3) слуховая косточка
4) овальное окно
5) преддверно-улитковый нерв
6) улитка

16. Установите последовательность событий, происходящих при свертывании крови. Запишите в таблицу соответствующую последовательность цифр.
1) разрушение тромбоцитов у места повреждения
2) превращение протромбина в тромбин
3) уплотнение рыхлой пробки тромбоцитов фибриновыми нитями
4) превращение фибриногена в фибрин
5) выделение тромбопластина
6) образование тромба

17. Прочитайте текст. Выберите три предложения, в которых даны описания географического видообразования. Запишите цифры, под которыми они указаны. (1)Видообразование происходит в результате расширения ареала исходного вида или при попадании популяции в новые условия. (2)Такое видообразование называют аллопатрическим. (3)Примером видообразования служит формирование двух подвидов погремка большого на одном лугу. (4)Естественный отбор способствовал формированию двух рас севанской форели, нерестящихся в разное время. (5)Репродуктивная изоляция особей не является обязательным условием видообразования. (6)Результатом изоляции является формирование эндемичных островных видов животных.

18. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Примеры антропогенных факторов воздействия:
1) разрушение озонового слоя под действием фреонов
2) гибель сусликов из-за пандемии
3) нарушение режима рек под влиянием деятельности бобров
4) разрыхление почв дождевыми червями
5) эвтрофикация водоемов из-за смыва удобрений
6) металлизация атмосферы

19. Установите соответствие между типами взаимоотношений и организмами, между которыми они устанавливаются: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.

20. Установите последовательность этапов эволюции животных, начиная с самых древних представителей. Запишите соответствующую последовательность цифр.
1) стегоцефал
2) зверозубый ящер
3) тушканчик
4) сеймурия
5) кистеперая рыба

21. Проанализируйте таблицу «Роль прокариотов в экосистемах». Заполните пустые ячейки таблицы, используя элементы, приведённые в списке. Для каждой ячейки, обозначенной буквой, выберите соответствующий элемент из предложенного списка. Список элементов:
1) Редуценты
2) Бактерии-хемосинтетики
3) Продуценты
4) Гетеротрофы
5) Бактерии-фотосинтетики
6) Денитрифицирующие
7) Автотрофы
8) Консументы

22. Проанализируйте диаграмму, отражающую содержание холестерола ЛПНП (липопротеинов низкой плотности) в плазме крови обследованных в лаборатории людей. Выберите все утверждения, которые можно сформулировать на основании анализа представленных данных. Запишите в ответе цифры, под которыми указаны выбранные утверждения.
1) Пятеро из обследованных людей имеют значение содержания холестерола-ЛПНП в интервале от 200 до 249 мг/дл.
2) Более 60% пациентов имеют чрезвычайно высокий риск развития атеросклероза.
3) Значение содержания холестерола-ЛПНП более 300 мг/дл смертельно.
4) Более 50% обследованных людей имеют от 75 до 149 мг/дл холестеролЛПНП в плазме крови.
5) В плазме крови 4% людей содержание холестерола-ЛПНП находится в пределах от 50 до 74 мг/дл.

23. Какая переменная в этом эксперименте будет зависимой (изменяющейся), а какая — независимой (задаваемой)? Объясните, как в данном эксперименте можно поставить отрицательный контроль. С какой целью необходимо такой контроль ставить? * Отрицательный контроль – это экспериментальный контроль, при котором изучаемый объект не подвергается экспериментальному воздействию при сохранении всех остальных условий.

24. Предположите, почему для обработки кукурузных полей используют 2,4- Д. Каким веществом по результату действия на двудольные растения является 2,4-дихлорфеноксиуксусная кислота?

25. Рассмотрите рисунок. Какие пары комплементарных азотистых оснований ДНК отмечены буквами А и Б? При содержании большего количества каких пар азотистых оснований молекула ДНК будет медленнее подвергаться денатурации при воздействии повышенной температуры? Ответ поясните.

26. Некоторые виды лишайников являются трехкомпонентными, то есть включают клетки трех видов организмов: гриба, зеленой водоросли и цианобактерии. Какие функции могут выполнять цианобактерии в составе такого лишайника? Назовите не менее двух. Какие преимущества имеет гриб в составе трехкомпонентного лишайника по сравнению с двухкомпонентным?

27. У животных существует несколько типов брачных отношений, например, моногамия – образование стойких супружеских пар, полигамия – спаривание особи одного пола со множеством партнеров противоположного пола. Большинство видов гнездовых птиц практикуют моногамные отношения, а большинство видов млекопитающих — полигамные. Объясните, почему для гнездовых птиц стратегия моногамного поведения наиболее выгодна. По каким причинам птицы, как правило, не могут практиковать полигамию, как это делают млекопитающие? Ответ поясните.

28. Какой хромосомный набор (n) характерен для клеток мегаспорангия и мегаспоры цветкового растения? Объясните, из каких исходных клеток и в результате какого деления образуются клетки мегаспорангия и мегаспора.

29. Существует два вида наследственной слепоты, каждый из которых определяется рецессивными аллелями генов (а или b). Оба аллеля находятся в различных парах гомологичных хромосом. Какова вероятность рождения слепой внучки в семье, в которой бабушки по материнской и отцовской линиям хорошо видят (не имеют рецессивных генов), а оба дедушки дигомозиготны и страдают различными видами слепоты? Составьте схему решения задачи. Определите генотипы и фенотипы бабушек и дедушек, их детей и возможных внуков.

Вам будет интересно: 

ЕГЭ по биологии 11 класс 2023. Новый тренировочный вариант №6 — №221121 (задания и ответы)

* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР

Поделиться:

Источник

Понравилась статья? Поделить с друзьями:
  • Решу егэ 509618
  • Решу егэ 508128
  • Решу егэ 509590
  • Решу егэ 508
  • Решу егэ 509588