Решите неравенство:
Спрятать решение
Решение.
Неравенство имеет смысл при то есть при
Пусть Тогда неравенство принимает вид
откуда
или
При всех допустимых x основание степени положительно и, следовательно,
Значит, неравенство выполняется только при
Выясним, при каких x это происходит:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
За это задание ты можешь получить 3 балла. На решение дается около 25 минут. Уровень сложности: повышенный.
Средний процент выполнения: 2.7%
Ответом к заданию 15 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 15:
Необходимо свести сложное неравенство к простейшему. Для этого нужно знать метод замены показательных и тригонометрических функций, помня про ограничения. Знать метод интервалов и метод рационализации для логарифмических, показательных и содержащих модуль неравенств.
Разбор сложных заданий в тг-канале
Задачи для практики
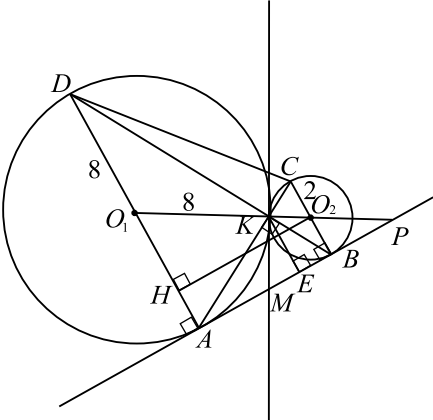
Задача 1
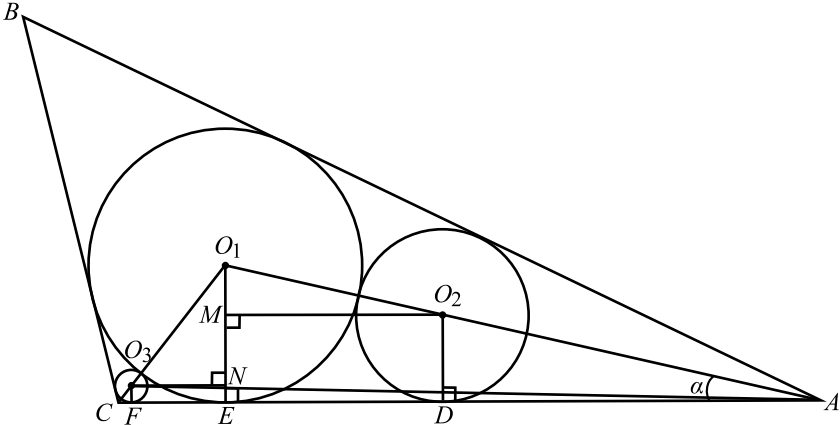
Окружность с центром $O_1$ радиусом $9$ вписана в треугольник $ABC$. Окружности с центрами $O_2$ и $O_3$ и радиусами ${81} / {25}$ и $1$, которые вписаны в углы треугольника $A$ и $C$ соответственно, касаются первой окружности внешним образом.
а) Докажите, что $∠ C=π-arctg {24} / {7}$.
б) Найдите площадь треугольника $AO_1O_3$.
Решение
a) Обозначим радиусы окружностей $r_1 = 9, r_2 = {81}/{25}, r_3 = 1$, а центры этих окружностей $O_1, O_2, O_3$ соответственно, и проведём радиусы $O_1E, O_2D, O_3F$ к точкам касания со стороной $AC$. Эти радиусы перпендикулярны касательной $AC$.
По свойству касательных, проведённых к окружности из одной точки, они образуют одинаковые углы с прямой, проходящей через центр окружности, то есть центры $O_1, O_2$ лежат на биссектрисе угла $A$, а центры $O_1, O_3$ — на биссектрисе угла $C$. Обозначим величину угла $C$ через $2β$. Тогда угол треугольника $O_1CA$ равен $β$.
Проведём $O_3N ⊥O_1E$, тогда $O_3N ‖ FE$ и $O_3N EF$ прямоугольник, $EN = r_3, O_1N = O_1E — EN = r_1 — r_3 = 8. ∠O_1CA = ∠O_1O_3N = β$ как соответственные при $O_3N ‖ AC$, секущая $CO_1$.
Треугольник $O_1O_3N$ прямоугольный, $O_3O_1= r_1 + r_3 = 10, O_3N = √{O_3O_1^2 — O_1N^2} = 6, tgβ = {O_1N}/{O_3N} = {8}/{6} = {4}/{3}$,
$tg 2β = {2 tg β}/{1 — tg^2 β} = {2 · {4}/{3}}/{1 — ({4}/{3})^2} = -{24}/{7}$.
Получили, что угол $C$ тупой. $∠C = π − arctg{24}/{7}$.
б) 1) $tg β = {O_1E}/{EC}, EC = r_1 : tg β = 9 : {4}/{3} = {27}/{4}$.
Обозначим величину угла $O_1AC$ треугольника через $α$. Найдём $EA = r_1 : tg α$.
Проведём $O_2M ⊥O_1E$, тогда аналогично пункту а) $EM = r_2$,
$O_1M = O_1E — EM = r_1 — r_2 = {144}/{25}, O_1O_2= r_1 + r_2 = {306}/{25}$.
$O_2M= √{O_1O_2^2 — O_1M^2} = {270}/{25}, tg α = {O_1M}/{O_2M} = {8}/{15}, AE = r_1 : tg α = 9 : {8}/{15} = {135}/{8}$.
$AC = AE + EC = {189}/{8}$.
$S_{AO_1O_3} = S_{AO_1C}-S_{ACO_3}={1}/{2}r_1· AC-{1}/{2}r_3·AC = {1}/{2}(r_1-r_3) ·AC = 94.5$.
Ответ: 94.5
Задача 2
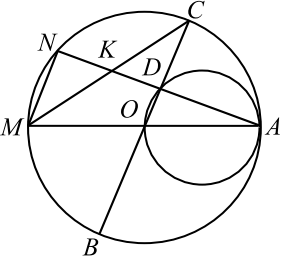
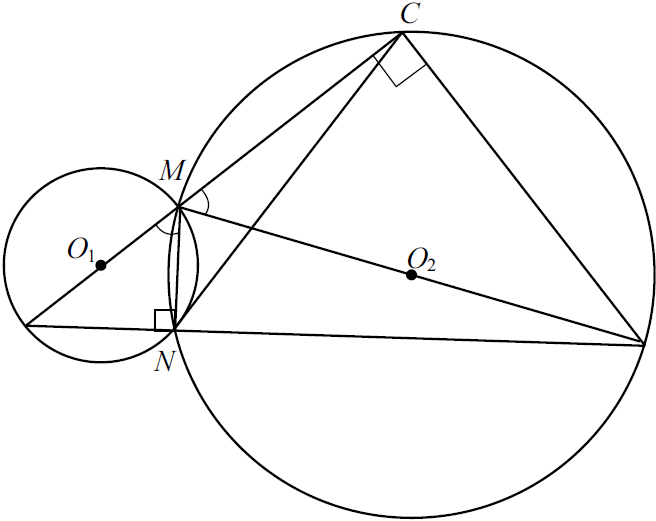
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают б’ольшую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {2√ {2}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж.
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны.
б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN , BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK}/{KA} = {MN}/{MA} = cos∠AM N = cos∠AOC = √{1-sin^2 ∠AOC} = {1}/{3}$.
Ответ: 1:3
Задача 3
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают большую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {√ {5}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж (см. рис.).
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны. б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN$, $BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK} / {KA} = {MN} / {MA} = cos ∠ AMN = cos ∠ AOC = √ {1 — sin^2 ∠ AOC} = {2} / {3}$.
Ответ: 2:3
Задача 4
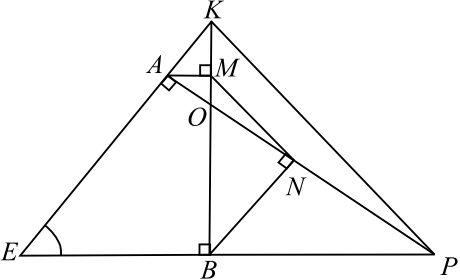
В треугольнике $EKP$, в котором все углы острые, проведены высоты $KB$ и $PA$. Из точек $A$ и $B$ на $KB$ и $PA$ опущены перпендикуляры $AM$ и $BN$ соответственно.
а) Докажите, что прямые $MN$ и $KP$ параллельны.
б) Найдите отношение $MN:KP$, если угол $KEP$ равен $45^°$.
Решение
а) $△POB ∼ △KOA$ по первому признаку подобия: $∠PBO = ∠OAK = 90°, ∠BOP = ∠AOK$ как вертикальные.
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OK} = {BN}/{AM}$ (1).
$△ONB ∼ △AOM$ по первому признаку подобия: $∠BNO = ∠AMO = 90°, ∠BON = ∠AOM$ как вертикальные, отсюда ${ON}/{OM} = {BN}/{AM}$ (2).
Из 1) и 2) следует ${OP}/{OK} = {ON}/{OM}$.
Следовательно, $△OPK ∼ △ONM$ по второму признаку подобия: $∠POK$ — общий, ${OP}/{ON} = {OK}/{OM}$.
Из подобия следует $∠OPK = ∠ONM$ . Углы $OPK$ и $ONM$ соответственные при прямых $PK$ и $NM$ и секущей $OP$ . Следовательно, $PK ‖ MN$ по признаку параллельности прямых.
б) В четырехугольнике $AEBO ∠AEB = 45°$ (по условию) $∠AOB=360°-(∠A +∠B +∠E ) = 360° — 225° = 135°$. В $△AOM ∠AMO = 90°, ∠AOM = 180°-135°=45°, AM=MO$.
Обозначим $OM = x$, тогда $AM = x, AO=OM√2=x√2$.
В $△OAK ∠OAK = 90°, ∠AOM = 45°$, то есть $AO = AK, AO=x√2, KO=AO√2=x√2·√2=2x$.
По доказанному в пункте а) $△OPK ∼ △ONM$, значит, ${MN}/{KP} = {OM}/{OK}$.
Пусть $OM = x, OK = 2x$.
${MN}/{KP}={x}/{2x}=1:2$
Ответ: 1:2
Задача 5
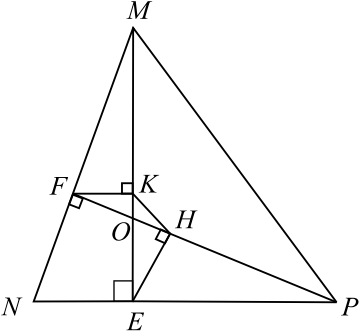
В треугольнике $MNP$, в котором все углы острые, проведены высоты $ME$ и $PF$. Из точек $F$ и $E$ на $ME$ и $PF$ опущены перпендикуляры $FK$ и $EH$ соответственно.
а) Докажите, что прямые $KH$ и $MP$ параллельны.
б) Найдите отношение $MP:KH$, если угол $MNP$ равен $60^°$.
Решение
а) $O$ — точка пересечения высот $ME$ и $PF$. $△POE ∼ △MFO$ по первому признаку подобия: $∠PEO = ∠OFM = 90°, ∠EOP = ∠FOM$ как вертикальные.
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OM} = {EH}/{FK}$ (1).
$△OHE ∼ △FOK$ по первому признаку подобия: $∠EHO = ∠FKO = 90°, ∠EOH = ∠FOK$ как вертикальные, отсюда ${OH}/{OK} = {EH}/{FK}$ (2).
Из 1) и 2) следует ${OP}/{OM} = {OH}/{OK}$.
Следовательно, $△OP M ∼ △OH K$ по второму признаку подобия: $∠P OM$ — общий, ${OP}/{OH} = {OM}/{OK}$.
Из подобия следует $∠OP M = ∠OH K$ . Углы $OP M$ и $OH K$ соответственные при прямых $M P$ и $K H$ и секущей $OP$ . Следовательно, $M P ‖ K H$ по признаку параллельности прямых.
б) В четырехугольнике $N FOE ∠FOE = 360° -(∠90° +∠90° +∠N ) = 360° — 240° = 120°$. В $△FOK ∠FKO = 90°, ∠FOK = 60°$, как смежный с $∠FOE = 120°$, тогда $∠OF K = 30°$.
Обозначим $OK = x$, тогда $FO = 2x$.
В $△OFM ∠M FO = 90°, ∠FOM = 60°, ∠F M O = 30°$, то есть $FO = {1}/{2}M O$, значит, $2x = {1}/{2}M O, M O = 4x$.
По доказанному в пункте а) $△OM P ∼ △OK H$, значит, ${MP}/{K H} = {M O}/{OK} $, но $M O = 4x, OK = x$, следовательно, ${M P}/{K H} = {4x}/{x} = 4 : 1$
Ответ: 4:1
Задача 6
В прямоугольном треугольнике $ABC$ точки $P$ и $K$ — середины катета $BC$ и гипотенузы $AB$ соответственно. Биссектриса угла $BAC$ пересекает прямую $KP$ в точке $R$.
а) Докажите, что точки $A$, $B$, $C$ и $R$ лежат на одной окружности.
б) Найдите отношение площадей треугольников $AKR$ и $BCR$, если $sin ∠ BAC={15} / {17}$.
Решение
а) Отрезок, соединяющий вершину прямого угла и середину гипотенузы, равен половине длины гипотенузы, то есть $AK = K B = K C. AR$ — биссектриса угла $BAC$, значит $∠CAR =∠BAR = α$.
$K P$ — средняя линия $△ABC$, значит, $K P ‖ AC$.
Накрест лежащие углы $CAR$ и $ARK$ равны (секущая $AR$).
В треугольнике $AK R$ равны углы $K AR$ и $K RA$, значит $AK = K R$.
Получим $AK = K B = K C = K R$, значит точки $A, B, C$ и $R$ лежат на окружности с центром $K$.
б) $∠CBR =∠CAR$ и $∠BAR =∠BCR$ (опираются на дуги $C R$ и $BR$ соответственно), таким образом, треугольники $AK R$ и $BC R$ подобны по двум углам. По теореме синусов для треугольника $ABR$ получим ${BR}/{sin ∠RAB} = 2r$, где $r$ — радиус описанной окружности, то есть $2r = AB$. Получили ${BR}/{AB} = sin ∠RAB = sin α$.
Но коэффициент подобия треугольников $AK R$ и $BC R$ равен ${AK}/{BR} = {2AK}/{2BR} = {AB}/{2BR} = {1}/{2 sin α}$.
По условию $sin ∠BAC = sin 2α = {15}/{17}$.
Тогда $cos 2α = √{1 — ({15}/{17})^2} = {8}/{17}$,
$cos 2α = 1 — 2 sin^2 α = {8}/{17}, 2 sin^2 α = {9}/{17}$.
Площади треугольников относятся как квадрат коэффициента подобия, поэтому ${S_{AKR}}/{S_{BCR}} = ({1}/{2sin α})^2 = {1}/{2 · {9}/{17}} = {17}/{18}$.
Ответ: 17:18
Задача 7
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $BE$ и $FD$ параллельны.
а) Докажите, что прямые $FC$ и $CD$ перпендикулярны.
б) Найдите отношение $BE:FD$, если угол $BCD$ равен $120°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет падать на продолжение $CD$, а не на саму сторону, что противоречит условию.
а) Для доказательства перпендикулярности прямых $FC$ и $CD$ достаточно доказать подобие треугольников $SFC$ и $SAE$.
Заметим, что $△SBC ∼ △SAD$ по двум углам ($∠SBC = ∠SAD = 90°, ∠S$ — общий). Тогда ${SB}/{SA} = {SC}/{SD}$, то есть $SB·SD = SA · SC$.
С другой стороны, $△SBE ∼ △SFD$ по двум углам: $∠SBE = ∠SFD$ как соответственные углы при параллельных прямых $BE$ и $FD$ и секущей $SA, ∠S$ — общий.
Тогда ${SB}/{SF} = {SE}/{SD}$, отсюда $SB · SD = SF · SE$.
Следовательно, $SA · SC = SB · SD = SF · SE$.
Тогда $SA · SC = SF · SE, {SA}/{SF} = {SE}/{SC}$.
Отсюда $△SAE ∼ △SFC$ по второму признаку.
Тогда $∠SCF = ∠SEA = 90°, FC ⊥ SD$, что и требовалось доказать.
б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE}/{FD} = {SB}/{SF}$.
$∠BCS = 180° — ∠BCD = 60°, SB = SC sin 60° = {√3}/{2}SC. ∠CSF = 90° — ∠BCS = 30°$. Из $△SFC$ следует, что $CS = SF cos 30° = SF {√3}/{2}$. Тогда $SB = {√3}/{2}SC ={√3}/{2}·{√3}/{2}SF; {SB}/{SF} = {3}/{4} = 0.75$.
Ответ: 0.75
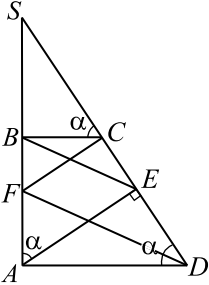
Задача 8
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $CD$ и $CF$ перпендикулярны. а) Докажите, что прямые $BE$ и $FD$ параллельны. б) Найдите отношение $BE:FD$, если угол $BCD$ равен $150°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. а) Для доказательства параллельности прямых $BE$ и $FD$ достаточно доказать, что треугольники $SBE$ и $SFD$ подобны (см. рис.). Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет опускаться на продолжение $CD$, а не на саму сторону, что противоречит условию. По условию $FC⊥ CD$ и $AE⊥ CD$, отсюда $FC∥ AE$. Заметим: в прямоугольных треугольниках $SCB$, $SFC$, $SAE$ и $SDA$ угол $S$ общий, значит, $∠ SCB=∠ SFC=∠ SAE=∠ SDA=α$. В каждом из рассматриваемых треугольников выразим $sin α$. $▵ SCB$: $sin α={SB} / {SC}$ (1) $▵ SFC$: $sin α={SC} / {SF}$ (2) $▵ SAE$: $sin α={SE} / {SA}$ (3) $▵ SDA$: $sin α={SA} / {SD}$ (4) Перемножив (1) на (2) и (3) на (4), получим ${SB} / {SC}⋅ {SC} / {SF}=sin^2 α$, ${SB} / {SF}=sin^2α$, ${SE} / {SA}⋅ {SA} / {SD}=sin^2α$, ${SE} / {SD}=sin^2α$. Отсюда ${SB} / {SF}={SE} / {SD}$. Имеем: две стороны $▵ SBE$ пропорциональны двум сторонам $▵ SFD$ и между ними угол $S$ — общий, значит, $▵ SBE∼ ▵ SFD$ по второму признаку подобия. Из подобия следует равенство соответственных углов $SEB$ и $SDF$ при прямых $BE$, $FD$ и секущей $SD$, следовательно, по признаку параллельности прямых $BE∥ FD$. б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE} / {FD}={SB} / {SF}$. В пункте а) доказано ${SB} / {SF}=sin^2 α$, $∠ BCD+α=180°$, $α=180°-150°=30°$. ${BE} / {FD}={SB} / {SF}=sin^2 30°=0{,}5^2=0{,}25$.
Ответ: 0.25
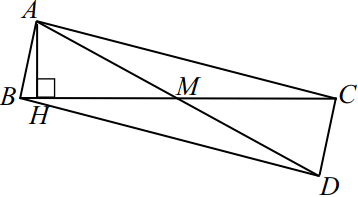
Задача 9
В треугольнике $ABC$ проведена высота $AH$ и медиана $AM$. $AB=2$, $AC=√ {21}$, $AM=2{,}5$.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Вычислите $HM$.
Решение
а) Достроим треугольник $ABC$ до параллелограмма $ABDC$, как показано на рисунке.
По свойству параллелограмма, верно равенство $2(AB^2 + AC^2) = AD^2 + BC^2$, или $2(AB^2 + AC^2) = (2AM)^2 + BC^2$. Так как по условию $AB = 2, AC = √{21}, AM = 2.5$, то $2(22 + √{21}^2) = (2 · 2.5)^2 + BC^2$, откуда $BC = 5$. Если диагонали параллелограмма равны, то он — прямоугольник, значит, $∠BAC = 90°$ и $△ABC$ прямоугольный.
б) В прямоугольном треугольнике $ABC$ выразим площадь двумя способами: $2S = AB · AC, 2S = BC · AH$, приравнивая правые части этих равенств, находим $AH = {AB·AC}/{BC} = {2 · √21}/{5}$. Катет $HM$ найдём из прямоугольного треугольника $AHM$ по теореме Пифагора: $HM = √{AM^2 − AH^2} = √{2.5^2 −({2 · √21}/{5})^2} = √{{25}/{4} − {84}/{25}} = √{{625 − 336}/{100}} = {17}/{10} = 1.7$.
Ответ: 1.7
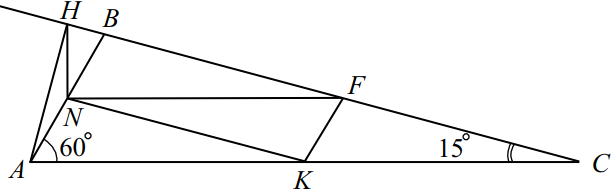
Задача 10
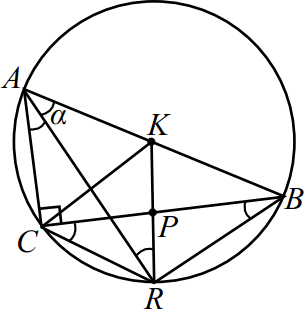
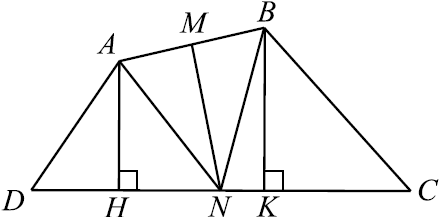
В треугольнике $ABC$ точки $K$, $N$, $F$ — середины сторон $AC$, $AB$ и $BC$ соответственно. $AH$ — высота треугольника $ABC$, $∠ CAB=60^°$, $∠ ACB=15^°$.
а) Докажите, что точки $K$, $N$, $F$ и $H$ лежат на одной окружности.
б) Найдите $FH$, если $BC=4√ 3$.
Решение
а) $∠ABC = 180° — (60° + 15°) = 105°$.
$NH$ — медиана в прямоугольном треугольнике $AHB$, отсюда $NH = NB = AN$.
$∠ABH = 75°, ∠BHN = ∠NBH$ как углы при основании равнобедренного треугольника $NBH , ∠NBH = 75°$.
$FK = {1}/{2}AB, NK = {1}/{2}BC , FN = {1}/{2}AC$ по свойству средней линии треугольника, тогда $△FKN ∼ △ABC$ по трём пропорциональным сторонам, следовательно, $∠NKF = ∠ABC = 105°$.
В четырёхугольнике $NHFK$ найдём сумму противоположных углов: $∠FKN + ∠FHN = 105° + 75° = 180°$, значит, около этого четырёхугольника можно описать окружность, что и требовалось доказать.
б) По теореме синусов для $△NFK: {NK}/{sin∠NFK} = 2R$, где $R$ — радиус окружности, проходящей через точки $K , N , F$ и $H$. Так как $NK = {1}/{2}BC$, то ${BC}/{2sin60°} = 2R = {4√3}/{2} : {√3}/{2} = 4$.
В равнобедренном треугольнике $HNB$ $∠N = 180° — 75°· 2 = 30°$. $∠BNF = ∠BAC = 60°$ как соответственные углы при параллельных прямых $NF$ и $AC$ и секущей $AB$.
В $△HNF ∠HNF = ∠HNB + ∠BNF = 30° + 60° = 90°$, значит $HF$ — диаметр описанной окружности, $HF = 2R = 4$.
Ответ: 4
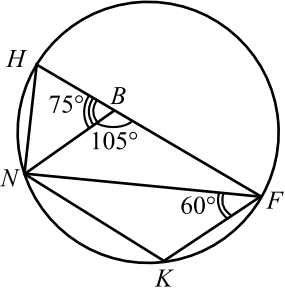
Задача 11
Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь $▵ AKB$, если известно, что радиусы окружностей равны $8$ и $2$.
Решение
а) Общая касательная, проведенная к окружностям в точке $K$, пересекает $AB$ в точке $M$. По свойству касательных, проведенных из одной точки, $AM = K M$ и $K M = BM$. Треугольник $AK B$, у которого медиана $K M$ равна половине стороны $AB$, к которой она проведена, прямоугольный, $∠AK B = 90°$. Вписанный угол $AK D$ прямой, поэтому он опирается на диаметр $AD$, значит, $AD ⊥ AB$. Аналогично, получаем, что $BC ⊥ AB$. Следовательно, прямые $AD$ и $BC$ параллельны.
б) Пусть первая окружность имеет радиус $8$, а вторая — радиус $2$.
Проведём $O_2H ⊥ AD$, тогда $O_2HAB$ — прямоугольник и $AH = O_2 B = 2, AB = O_2 H$. Из $△O_1O_2H$ получим $O_2 H^2 = O_1O_2^2 — O_1H^2 = (2 + 8)^2 — (8 — 2)^2 = 64, O_2 H = 8 = AB$.
$△O_2PB ∼ △O_1O_2H$ (по двум углам), ${O_2B}/{O_2P} = {O_1H}/{O_1O_2}; {2}/{O_2P} = {8 — 2}/{8 + 2}; O_2P = {10}/{3}$.
Проведём высоту $KE$ в $△AKB$, получим, что $△O_2BP ∼ △KEP$ (по двум углам). ${KE}/{O_2B} = {KP}/{O_2P}; {KE}/{2} = {2 + {10}/{3}}/{{10}/{3}}; KE = 1.6 · 2 = 3.2$.
$S_{AKB} = {1}/{2}AB · KE = {1}/{2} · 8 · 3.2 = 12.8$.
Ответ: 12.8
Задача 12
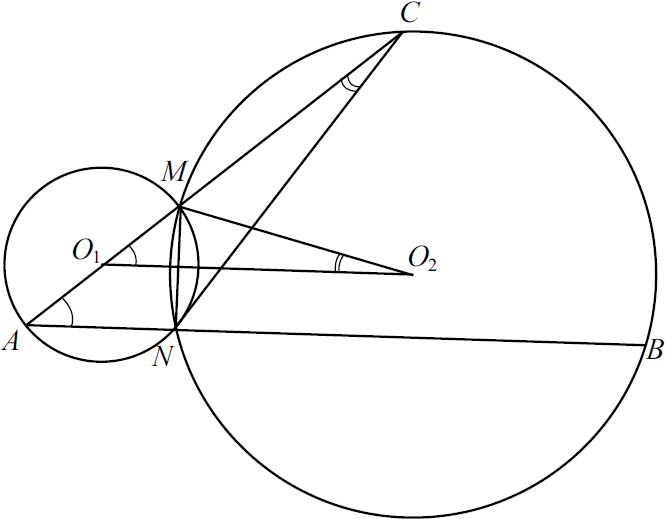
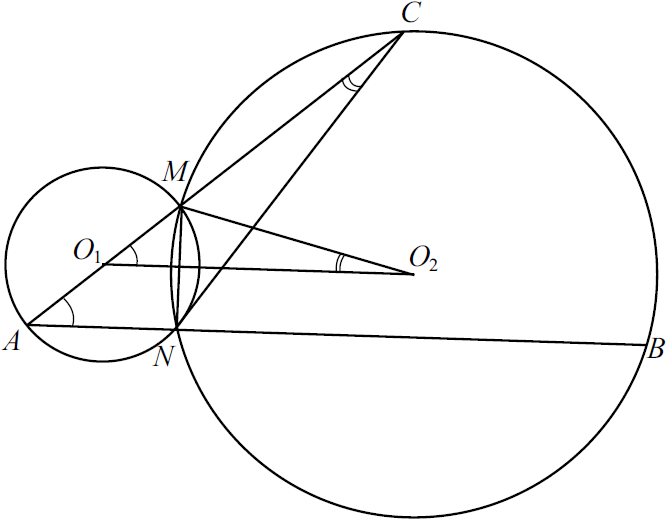
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $1{,}5$ раза больше радиуса первой и $MN=3$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O_2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $1.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠MNA = 90°$, тогда $MB$ — диаметр окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
Значит, $△AMN∼△BCM$ по двум углам.
Значит, ${MC}/{MN} = {MB}/{AM}={2⋅3r}/{2⋅2r} =1.5.$
$MC= 1.5·3 = 4.5$.
Ответ:
Задача 13
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $2{,}5$ раза больше радиуса первой и $MN=2$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $2.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠ANM = 90°$, тогда $MB$ — диаметр второй окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
Значит, $△AMN∼△BCM$ по двум углам ($∠ANM = ∠MCB = 90°, ∠AMN = ∠CMB$)
${MC}/{MN} = {MB}/{AM}$, но ${MB}/{AM} = {2·2.5r}/{2r} = 2.5$.
$MC = 2.5·MN = 5$.
Ответ: 5
Задача 14
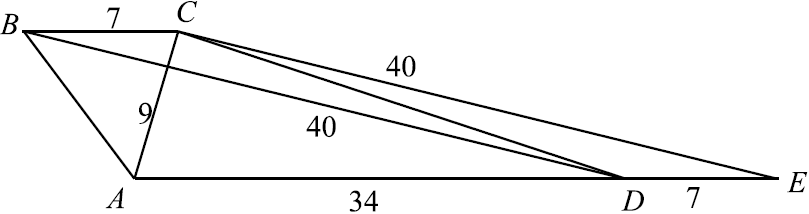
Основания трапеции равны $7$ и $34$, а её диагонали равны $9$ и $40$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
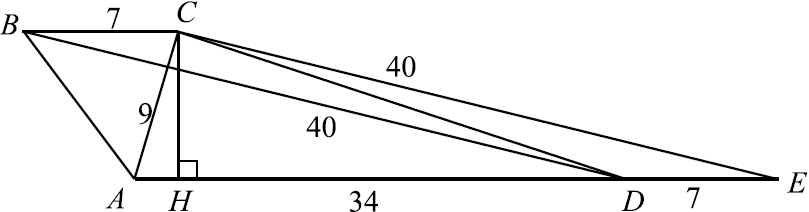
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 7$, тогда $AE = AD + DE = 34 + 7 = 41$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {9·40}/{41}. S_{ABCD} = {AD + BC}/{2}·CH = {34 + 7}/{2}·{9·40}/{41} = 9·20 = 180$.
Ответ: 180
Задача 15
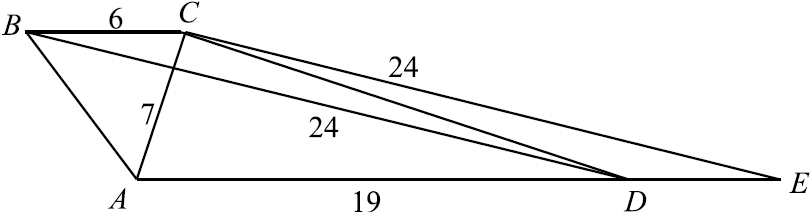
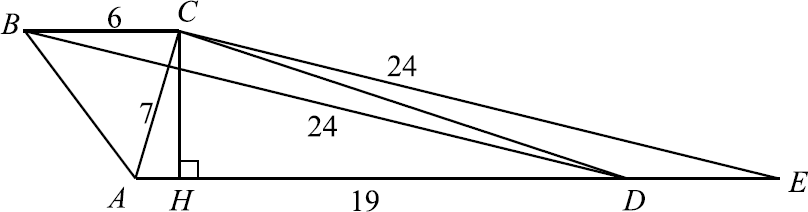
Основания трапеции равны $6$ и $19$, а её диагонали равны $7$ и $24$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 6$, тогда $AE = AD + DE = 19 + 6 = 25$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {7·24}/{25}. S_{ABCD} = {AD + BC}/{2}·CH = {19 + 6}/{2}·{7·24}/{25} = 7·12 = 84$.
Ответ: 84
Задача 16
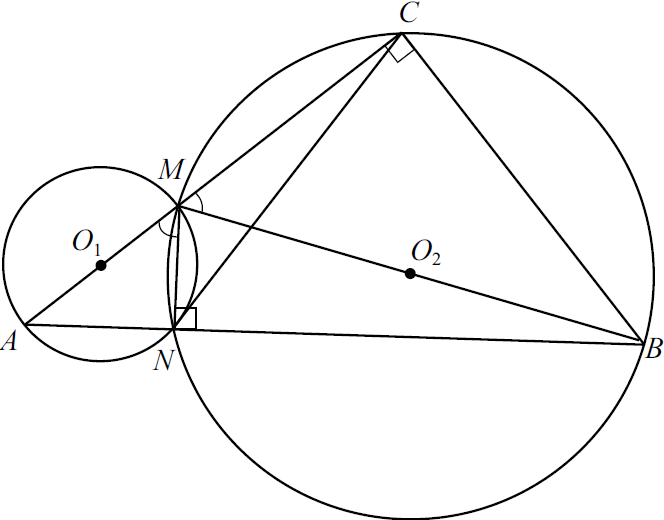
Две окружности касаются внутренним образом в точке $K$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $AB$ большей окружности вторично пересекает меньшую окружность в точке $C$, отличной от $K$. Лучи $KO$ и $KC$ вторично пересекают большую окружность в точках $D$ и $E$ соответственно. Точка $B$ лежит на дуге $EK$ большей окружности, не содержащей точку $D$.
а) Докажите, что прямые $DE$ и $AB$ параллельны.
б) Известно, что $sin∠ KOB = {√ {15}} / {8}$. Прямые $DB$ и $EK$ пересекаются в точке $L$. Найдите отношение $EL:LK$.
Решение
а) $KD$ — диаметр большей окружности ($O ∈ KD$), $O_1$ — центр меньшей окружности, $l$ — общая касательная двух окружностей, проходящая через точку $K$ (см. рис.). $O_1 ∈ KD$. Действительно, $OK⊥ l$, $O_1K⊥ l$ как радиусы, проведённые в точку касания, значит, точки $O$, $K$, $O_1$ лежат на луче $KO$. $∠ DEK=∠ OCK=90°$ как вписанные углы, опирающиеся на диаметры $DK$ и $OK$ соответственно. $C∈ EK$, следовательно, $DE∥ AB$ как два перпендикуляра к одной прямой.
б) Так как диаметр $AB$, перпендикулярный хорде $EK$, делит её пополам, то $CE=CK$, следовательно, $⌣ KB=⌣ BE$ (см. рис.). Угол $EDK$ вписанный, опирается на дугу $EK$, а угол $BOK$ — центральный, опирается на половину дуги $EK$, следовательно, $∠ EDK=∠ BOK=α$; $∠ EDB=∠ BDK$ как вписанные углы, опирающиеся на равные дуги, тогда $DL$ — биссектриса треугольника $DEK$, а по свойству биссектрисы ${EL} / {LK}={DE} / {DK}=cos α=√ {1-sin^2 α}$.
${EL} / {LK}=√ {1-{15} / {64}}={7} / {8}$.
Ответ: fsm78
Задача 17
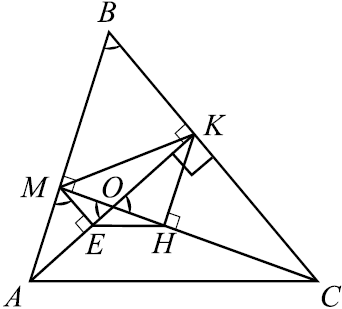
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $cos ∠ ABC = {√ {2}} / {4}$.
Решение
а) По условию задачи выполним чертёж.
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = {2}/{16} ={1}/{8}$. Таким образом, $EH : AC = 1 : 8$.
Ответ: 1:8
Задача 18
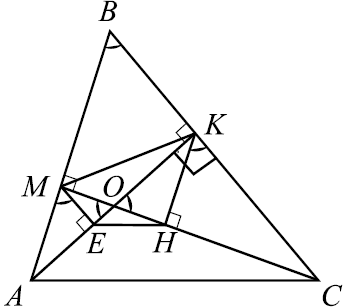
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $sin ∠ ABC = {√ {3}} / {3}$.
Решение
а) По условию задачи выполним чертёж.
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = 1-sin^2∠ABC = 1-{1}/{3} ={2}/{3}$. Таким образом, $EH : AC = 2 : 3$.
Ответ: 2:3
Задача 19
Один из двух отрезков, соединяющих середины противоположных сторон выпуклого четырёхугольника, делит его площадь пополам, а другой — в отношении ${6} / {7}$. а) Докажите, что данный четырёхугольник есть трапеция. б) Укажите отношение двух оснований этой трапеции (меньшего к большему).
Решение
а) Рассмотрим выпуклый четырёхугольник ABCD. Пусть M — середина AB, N — середина CD, причём $S_{AMND} = S_{MBCN}$. Проведём AN и BN. Заметим, что $S_{AMN} = {1}/{2}AM · MNsin∠AMN ={1}/{2}MB · MNsin∠BMN = S_{BMN}$, так как $AM = MB, sin∠AMN = sin(180° — ∠AMN) = sin∠BMN$.
Отсюда $S_{AND} = S_{BNC}(S_{AND} = S_{AMND} — S_{AMN}, S_{BNC} = S_{MBCN} — S_{MBN})$.
Опустим в $△AND$ высоту AH, в $△BNC$ — высоту BK.
Получим ${1}/{2}DN·AH = {1}/{2}NC·BK$, при этом $DN = NC$. Следовательно, $AH = BK$. Но тогда в четырёхугольник $AHKB ∠AHK = ∠BKH = 90°, AH = BK$, то есть $AHKB$ — прямоугольник. Значит, $AB ‖ HK, AB ‖ DC$.
Для доказательства того, что ABCD — трапеция, необходимо доказать, что две другие стороны не параллельны, то есть AD не параллельна BC. Предположим противное. Тогда ABCD — параллелограмм, но тогда отрезок, соединяющий середины AD и BC, делит площадь ABCD пополам, что противоречит условию, так как отношение полученных площадей должно равняться 6 : 7. Отсюда верно ABCD — трапеция.
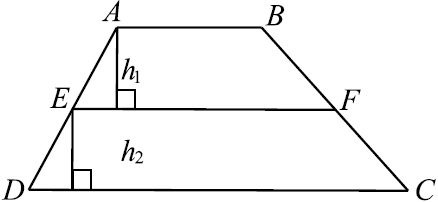
б) По условию EF делит площадь ABCD на площади, отношение которых равно 6 : 7, а именно $S_{ABFE} : S_{EFCD} = 6 : 7$.
$EF$ — средняя линия, $EF = {AB + CD}/{2}$.
Надо найти AB : CD.
$S_{ABFE} = {AB + EF}/{2}·h_1, S_{EFCD} = {EF + CD}/{2}·h_2$, где $h_1$ — высота $ABFE$, $h_2$ — высота $EFCD$.
Учитывая, что $AB ‖ CD$, а $EF$ — средняя линия и $EF ‖ AB$ и $EF ‖ CD$, то расстояние от $EF$ до $AB$ и от $EF$ до $CD$ равны, то есть $h_1 = h_2$.
Следовательно, ${S_{ABFE}}/{S_{EFCD}} = {{AB + EF}/{2}}/{{EF + CD}/{2}} = {AB + EF}/{EF + CD} = {AB + {AB + CD}/{2}}/{{AB + CD}/{2} + CD} = {3AB + CD}/{3CD + AB}, {3AB + CD}/{3CD + AB} = {6}/{7}, 21AB + 7CD = 18CD + 6AB, 15AB = 11CD, {AB}/{CD} = {11}/{15}$.
$AB : CD = 11 : 15$.
Ответ: 11:15
Задача 20
В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении $9:13$. а) Доказать, что данный четырёхугольник является трапецией. б) Найти отношение меньшего основания этой трапеции к большему.
Решение
а) Рассмотрим выпуклый четырёхугольник $QMNP$ (см. рис.). Пусть $E$ — середина $MQ$, $F$ — середина $NP$, причём $S_{MNFE}=S_{EFPQ}$.
Проведём отрезки $EN$ и $EP$. Заметим, что
$S_{▵ EFN}={1} / {2} EF⋅ FNsin ∠ EFN={1} / {2} EF⋅ FP sin ∠ EFP=S_{▵ EFP}$, так как $NF=FP$ и $sin ∠ EFN=sin (180°-∠ EFN)=sin ∠ EFP$. Отсюда $S_{▵ MNE}=S_{▵ EPQ}$ ($S_{▵ MNE}=S_{MNFE}-S_{▵ EFN}$, $S_{▵ EPQ}=S_{EFPQ}-S_{▵ EFP}$). Опустим в $▵ MNE$ высоту $NN_1$, в $▵ EPQ$ — высоту $PP_1$. Получим: ${1} / {2} ME⋅ NN_1={1} / {2} EQ⋅ PP_1$. Но $ME=EQ$, следовательно, $NN_1=PP_1$. Но тогда в четырёхугольнике $N_1NPP_1$ $∠ NN_1P_1=∠ N_1P_1P=90°$, $NN_1=PP_1$, то есть $N_1NPP_1$ — прямоугольник. Значит, $N_1P_1∥ NP$, $MQ∥ NP$. Из предположения о том, что $MN∥ QP$, следует, что отрезок, соединяющий середины сторон $MN$ и $QP$, делит параллелограмм $MNPQ$ на две равновеликие фигуры. Но по условию это не так. Значит, $MN ∦ QP$. Следовательно, $MNPQ$ — трапеция. б) По условию второй отрезок $AB$ делит четырёхугольник так, что площадь $ANPB$ относится к площади $ABQM$ как $9:13$ (см. рис.).
$S_{ANPB}:S_{ABQM}=9:13$. $AB$ — средняя линия трапеции, $AB={NP+MQ} / {2}$. $S_{ANPB}={AB+NP} / {2}⋅ h_1$; $S_{ABQM}={AB+MQ} / {2}⋅ h_2$, где $h_1$ — высота трапеции $ANPB$; $h_2$ — высота трапеции $ABQM$. Так как $NP∥ MQ$, а $AB$ — средняя линия и $AB∥ NP$ и $AB∥ MQ$, то расстояния от $AB$ до $NP$ и от $AB$ до $MQ$ равны, то есть $h_1=h_2$. Отсюда, ${S_{ANPB}} / {S_{ABQM}}={{NP+AB} / {2}} / {{AB+MQ} / {2}}={NP+{NP+MQ} / {2}} / {{NP+MQ} / {2}+MQ}={3NP+MQ} / {3MQ+NP}$, ${3NP+MQ} / {3MQ+NP}={9} / {13}$, $39NP+13MQ=27MQ+9NP$, $30NP=14MQ$, ${NP} / {MQ}={14} / {30}={7} / {15}$.
Ответ: 7:15
Рекомендуемые курсы подготовки

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки. Ответами к заданиям 1–22 являются последовательность цифр, число или слово (словосочетание). Ответы запишите в поля ответов в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ № 1 справа от номеров соответствующих заданий, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Скачать тренировочный вариант ЕГЭ: Скачать
Скачать ответы на тренировочный вариант ЕГЭ: Скачать
Задания:
1. Рассмотрите таблицу «Методы биологических исследований» и заполните ячейку, вписав соответствующий термин. Применяется для выявления геномных мутаций.
2. Исследователь добавлял в стакан коровьего молока желудочный сок собаки. Как спустя час в стакане изменится содержание дисахарида лактозы и животных жиров? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
3. Площадь земель, покрытых лесом, в России составляет примерно 1200 млн га. Известно, что 12 га леса связывают 18 тонн диоксида углерода в год. Сколько млн тонн углекислого газа может быть связано за год за счет российских лесов?
4. Определите вероятность (в %) гибели от анемии ребенка, родившегося в браке гомозиготных по рецессивному аллелю родителей, если эта форма анемии наследуется как аутосомный доминантный признак. В ответ запишите только соответствующее число.
5. Каким номером на рисунке обозначена структура, образующая спираль в сперматозоидах млекопитающих?
6. Установите соответствие между характеристиками и структурами, обозначенными на рисунке цифрами 1, 2, 3, 4: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
7. Выберите три признака, которые соответствуют описаниям селекции. Запишите в таблицу цифры, под которыми они указаны.
1) выведение новых штаммов микроорганизмов
2) получение новых семейств растений
3) получение генномодифицированных растений
4) выведение тритикале при скрещивании пшеницы и ржи
5) получение рекомбинантной плазмиды
6) выведение пород животных и сортов растений
8. Установите последовательность этапов ферментативного катализа. Запишите в таблицу соответствующую последовательность цифр.
1) образование нестабильного комплекса фермент-продукт
2) сближение фермента и субстрата
3) начало распада комплекса фермент-продукт
4) формирование фермент-субстратного комплекса
5) высвобождение продукта и фермента
9. Какой цифрой на рисунке обозначена вторичная полость тела?
10. Установите соответствие между характеристиками и структурами тела дождевого червя, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
11. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Для растения, изображенного на рисунке, характерно:
1) гаметофит обоеполый — содержит архегонии и антеридии
2) дихотомическое ветвление
3) заросток сердцевидной формы
4) споры созревают в сорусах
5) споры образуются в спороносных колосках
6) гаметофит формирует вайи
12. Установите последовательность систематических групп, начиная с самого низкого ранга. Запишите в таблицу соответствующую последовательность цифр.
1) Эукариоты
2) Членистоногие
3) Ежемухи
4) Ежемуха свирепая
5) Двукрылые
6) Животные
13. Какой цифрой на рисунке указан тип научения, который изучал К. Лоренц?
14. Установите соответствие между характеристиками и типами научения, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
15. Выберите три верно обозначенные подписи к рисунку «Строение уха». Запишите цифры, под которыми они указаны.
1) серная (церуминозная) железа
2) наружный слуховой проход
3) слуховая косточка
4) овальное окно
5) преддверно-улитковый нерв
6) улитка
16. Установите последовательность событий, происходящих при свертывании крови. Запишите в таблицу соответствующую последовательность цифр.
1) разрушение тромбоцитов у места повреждения
2) превращение протромбина в тромбин
3) уплотнение рыхлой пробки тромбоцитов фибриновыми нитями
4) превращение фибриногена в фибрин
5) выделение тромбопластина
6) образование тромба
17. Прочитайте текст. Выберите три предложения, в которых даны описания географического видообразования. Запишите цифры, под которыми они указаны. (1)Видообразование происходит в результате расширения ареала исходного вида или при попадании популяции в новые условия. (2)Такое видообразование называют аллопатрическим. (3)Примером видообразования служит формирование двух подвидов погремка большого на одном лугу. (4)Естественный отбор способствовал формированию двух рас севанской форели, нерестящихся в разное время. (5)Репродуктивная изоляция особей не является обязательным условием видообразования. (6)Результатом изоляции является формирование эндемичных островных видов животных.
18. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Примеры антропогенных факторов воздействия:
1) разрушение озонового слоя под действием фреонов
2) гибель сусликов из-за пандемии
3) нарушение режима рек под влиянием деятельности бобров
4) разрыхление почв дождевыми червями
5) эвтрофикация водоемов из-за смыва удобрений
6) металлизация атмосферы
19. Установите соответствие между типами взаимоотношений и организмами, между которыми они устанавливаются: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
20. Установите последовательность этапов эволюции животных, начиная с самых древних представителей. Запишите соответствующую последовательность цифр.
1) стегоцефал
2) зверозубый ящер
3) тушканчик
4) сеймурия
5) кистеперая рыба
21. Проанализируйте таблицу «Роль прокариотов в экосистемах». Заполните пустые ячейки таблицы, используя элементы, приведённые в списке. Для каждой ячейки, обозначенной буквой, выберите соответствующий элемент из предложенного списка. Список элементов:
1) Редуценты
2) Бактерии-хемосинтетики
3) Продуценты
4) Гетеротрофы
5) Бактерии-фотосинтетики
6) Денитрифицирующие
7) Автотрофы

22. Проанализируйте диаграмму, отражающую содержание холестерола ЛПНП (липопротеинов низкой плотности) в плазме крови обследованных в лаборатории людей. Выберите все утверждения, которые можно сформулировать на основании анализа представленных данных. Запишите в ответе цифры, под которыми указаны выбранные утверждения.
1) Пятеро из обследованных людей имеют значение содержания холестерола-ЛПНП в интервале от 200 до 249 мг/дл.
2) Более 60% пациентов имеют чрезвычайно высокий риск развития атеросклероза.
3) Значение содержания холестерола-ЛПНП более 300 мг/дл смертельно.
4) Более 50% обследованных людей имеют от 75 до 149 мг/дл холестеролЛПНП в плазме крови.
5) В плазме крови 4% людей содержание холестерола-ЛПНП находится в пределах от 50 до 74 мг/дл.
23. Какая переменная в этом эксперименте будет зависимой (изменяющейся), а какая — независимой (задаваемой)? Объясните, как в данном эксперименте можно поставить отрицательный контроль. С какой целью необходимо такой контроль ставить? * Отрицательный контроль – это экспериментальный контроль, при котором изучаемый объект не подвергается экспериментальному воздействию при сохранении всех остальных условий.
24. Предположите, почему для обработки кукурузных полей используют 2,4- Д. Каким веществом по результату действия на двудольные растения является 2,4-дихлорфеноксиуксусная кислота?
25. Рассмотрите рисунок. Какие пары комплементарных азотистых оснований ДНК отмечены буквами А и Б? При содержании большего количества каких пар азотистых оснований молекула ДНК будет медленнее подвергаться денатурации при воздействии повышенной температуры? Ответ поясните.
26. Некоторые виды лишайников являются трехкомпонентными, то есть включают клетки трех видов организмов: гриба, зеленой водоросли и цианобактерии. Какие функции могут выполнять цианобактерии в составе такого лишайника? Назовите не менее двух. Какие преимущества имеет гриб в составе трехкомпонентного лишайника по сравнению с двухкомпонентным?
27. У животных существует несколько типов брачных отношений, например, моногамия – образование стойких супружеских пар, полигамия – спаривание особи одного пола со множеством партнеров противоположного пола. Большинство видов гнездовых птиц практикуют моногамные отношения, а большинство видов млекопитающих — полигамные. Объясните, почему для гнездовых птиц стратегия моногамного поведения наиболее выгодна. По каким причинам птицы, как правило, не могут практиковать полигамию, как это делают млекопитающие? Ответ поясните.
28. Какой хромосомный набор (n) характерен для клеток мегаспорангия и мегаспоры цветкового растения? Объясните, из каких исходных клеток и в результате какого деления образуются клетки мегаспорангия и мегаспора.
29. Существует два вида наследственной слепоты, каждый из которых определяется рецессивными аллелями генов (а или b). Оба аллеля находятся в различных парах гомологичных хромосом. Какова вероятность рождения слепой внучки в семье, в которой бабушки по материнской и отцовской линиям хорошо видят (не имеют рецессивных генов), а оба дедушки дигомозиготны и страдают различными видами слепоты? Составьте схему решения задачи. Определите генотипы и фенотипы бабушек и дедушек, их детей и возможных внуков.
Вам будет интересно:
ЕГЭ по биологии 11 класс 2023. Новый тренировочный вариант №6 — №221121 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться: