Решу егэ 508766 - Помощь в подготовке к экзаменам и поступлению

Задания

Версия для печати и копирования в MS Word

Тип 4 № 508766

При двукратном бросании игральной кости в сумме выпало 6 очков. Какова вероятность того, что хотя бы раз выпало 3 очка?

Спрятать решение

Решение.

При двукратном бросании игральной кости 6 очков может получится только в пяти случаях: 1 + 5, 2 + 4, 3 + 3, 4 + 2 и 5 + 1. При этом 3 очка выпадало только в одном из этих случаев. Значит, вероятность того, что хотя бы раз выпало 3 очка равна

Ответ: 0,2.

Аналоги к заданию № 508761: 508762 508763 508764 508765 508766 508767 508768 Все

Кодификатор ФИПИ/Решу ЕГЭ: 6.3.1 Вероятности событий, 6.3.2 Использования вероятностей и статистики при решении прикладных задач

Спрятать решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Источник

Решение 26 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023

Скачать сборник в pdf

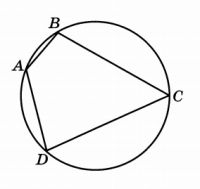
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 127°. Найдите угол BCD. Ответ дайте в градусах.

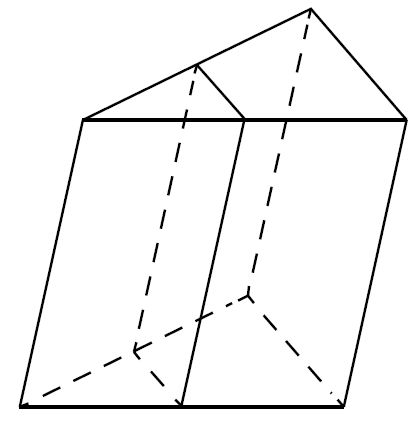
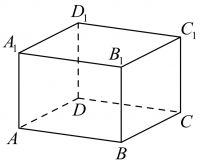
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что AB=9, BC=8, AA₁=6. Найдите объём многогранника, вершинами которого являются точки A, B, C, B₁.

В магазине в одной коробке лежат вперемешку ручки с черными, синими и красными чернилами, одинаковые на вид. Покупатель случайным образом выбирает одну ручну. Вероятность того, что она окажется черной, равна 0,36, а того, что она окажется красной, равна 0,26. Найдите вероятность того, что ручка окажется синей.

При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,97?

Найдите корень уравнения (sqrt{-x}=x+6). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Найдите значение выражения (cosalpha), если (mathrm{tg,} alpha=dfrac{sqrt{91}}{3}) и (alphainbigg(pi;dfrac{3pi}{2}bigg)).

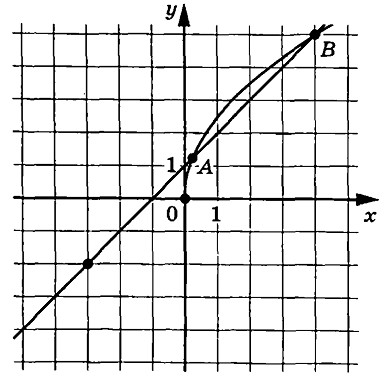
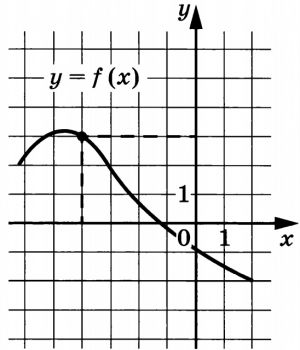
На рисунке изображён график функции (y=f(x)). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой (-4). Найдите значение производной функции в точке (x_0=-4).

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с фокусным расстоянием (f = 60 ,см). Расстояние (d_1) от линзы до лампочки может изменяться в пределах от 95 см до 115 см а расстояние (d_2) от линзы до экрана — в пределах от 140 см до 160 см. Изображение на экране будет чётким, если выполнено соотношение (dfrac1{d_1}+dfrac1{d_2}=dfrac1{f}). На каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким? Ответ дайте в сантиметрах.

Первый и второй насосы наполняют бассейн за 35 минут, второй и третий — за 40 минут, а первый и третий — за 56 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?

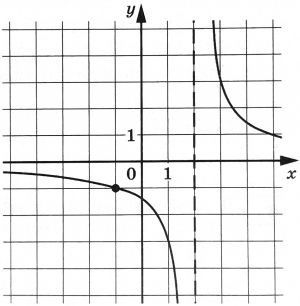
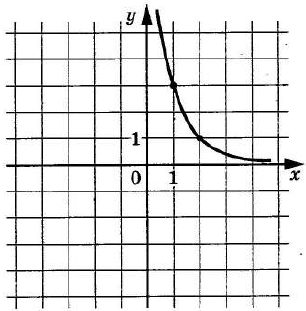
На рисунке изображён график функции (f(x)=dfrac{k}{x+a}). Найдите значение (x), при котором (f(x)=-0{,}2).

Найдите наибольшее значение функции (y=(x-6)e^{7-x}) на отрезке ([2;15]).

а) Решите уравнение (sin^2bigg(dfrac{x}{4}+dfrac{pi}{4}bigg)sin^2bigg(dfrac{x}{4}-dfrac{pi}{4}bigg)=0,375sin^2bigg(-dfrac{pi}{4}bigg)).

б) Найдите все корни этого уравнения, принадлежащие отрезку ([-3pi;pi]).

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.

а)

1. 2πn, n∈Z	2. π/6+2πn, n∈Z	3. π/4+2πn, n∈Z	4. π/3+2πn, n∈Z
5. π/2+2πn, n∈Z	6. 2π/3+2πn, n∈Z	7. 3π/4+2πn, n∈Z	8. 5π/6+2πn, n∈Z
9. π+2πn, n∈Z	10. -π/6+2πn, n∈Z	11. -π/4+2πn, n∈Z	12. -π/3+2πn, n∈Z
13. -π/2+2πn, n∈Z	14. -2π/3+2πn, n∈Z	15. -3π/4+2πn, n∈Z	16. -5π/6+2πn, n∈Z

б)

17. -3π	18. -8π/3	19. -7π/3	20. -2π
21. -5π/3	22. -4π/3	23. -π	24. -2π/3
25. -π/3	26. 0	27. π/3	28. 2π/3
29. π

В правильной шестиугольной призме (ABCDEFA_1B_1C_1D_1E_1F_1) сторона основания (AB) равна 6, а боковое ребро (AA_1) равно (5sqrt3). На ребре (DD_1) отмечена точка (M) так, что (DM:MD_1=2:3). Плоскость (alpha) параллельна прямой (A_1F_1) и проходит через точки (M) и (B).
а) Докажите, что сечение призмы (ABCDEFA_1B_1C_1D_1E_1F_1) плоскостью (alpha) — равнобедренная трапеция.
б) Найдите объём пирамиды, вершиной которой является точка (A_1), а основанием — сечение призмы (ABCDEFA_1B_1C_1D_1E_1F_1) плоскостью (alpha).

Решите неравенство (left(5cdot 0{,}2^{x+0{,}5}-0{,}2cdot5^{x+0{,}5}right)left(0{,}5log^2_{0{,}2}(x+0{,}5)-2log_5(x+0{,}5)right)>0).

15 января планируется взять кредит в банке на 3 года. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что за 24-й месяц кредитования нужно выплатить 45,2 тыс. рублей.
Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?

В прямоугольнике (ABCD) диагонали пересекаются в точке (О), а угол (BDC) равен (22{,}5^circ). Точка (P) лежит вне прямоугольника, а угол (BPC) равен (135^circ).
а) Докажите, что углы (BCP) и (POB) равны.
б) Прямая (PO) пересекает сторону (AD) в точке (F). Найдите (DF), если (BP=7) и (CP=5sqrt2).

Найдите все значения (a), при каждом из которых среди корней уравнения (x^2-10x+35=a|x-6|) будет ровно два положительных.

У Коли в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 2-рублёвая. Если взять 25 монет, то среди них обязательно найдётся хотя бы одна 5-рублёвая. Если взять 30 монет, то среди них обязательно найдётся хотя бы одна 10-рублёвая.
а) Может ли у Коли быть 50 монет?
б) Какое наибольшее количество монет может быть у Коли?
в) Какая наибольшая сумма рублей может быть у Коли?

Введите ответ в форме строки «да;123;1234». Где ответы на пункты разделены «;», и первый ответ с маленькой буквы.

Источник

508780 решу егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 14 № 508380

Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:

Приведем другое решение:

Как и в первом решении запишем неравенство в виде:

Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:

Задание 14 № 508380

—>

508780 решу егэ математика.

Ege. sdamgia. ru

07.03.2017 0:00:13

2017-03-07 00:00:13

Источники:

Https://ege. sdamgia. ru/problem? id=508380

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика

508780 решу егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 10 № 508781

Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?

Задание 10 № 508782

Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?

Задание 10 № 508783

Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508784

Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508785

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508786

Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508787

Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508788

Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508789

Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508790

Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508786

Задание 10 № 508781

Задание 10 508786.

Ege. sdamgia. ru

14.05.2019 20:28:53

2019-05-14 20:28:53

Источники:

Https://ege. sdamgia. ru/test? likes=508780

508780 решу егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 10 № 508780

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей

—>

Задание 10 № 508780

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Ege. sdamgia. ru

09.08.2017 16:57:34

2017-08-09 16:57:34

Источники:

Https://ege. sdamgia. ru/problem? id=508780

Источник

Новый тренировочный вариант №25367016 ЕГЭ 2022 по русскому языку 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.

Тренировочный вариант по русскому (КИМ): задания | ответы

Решу ЕГЭ 2022 по русскому языку тренировочный вариант №25367016

Ответы для варианта:

Шаровая молния— это образование, вызванное созданием при ударе обычной молнии газообразных химически активных веществ, которые горят в присутствии катализатора, например частичек дыма или пыли (известный советский физик-теоретик Я.И. Френкель). Но, к сожалению, пока мы не знаем веществ с […] колоссальной теплотворной способностью, которой обладает вещество шаровой молнии.

Есть ли у нас возможности оценить энергию молнии? Для этого имеются два «свидетельских показания»: одно— из газеты «Дейли Мейл», другое— сообщение пассажиров французского экспресса. В первом случае молния попала в бочку с водой, стоявшую на улице в ноябре. Температура воды, таким образом, может быть грубо определена. Вода была нагрета до кипения, ее было, как выяснилось, около 20 литров, причем некоторое количество— около 4 литров— выкипело.

Молния была размером «с большой апельсин», шар не упал с неба, а, как указывает автор заметки, «спустился». Следовательно, плотность вещества шаровой молнии лишь немного больше плотности воздуха (иногда молнии «плавают» в воздухе— тогда их плотность равна плотности воздуха). Воздух в объеме большого апельсина весит примерно десятые доли грамма. Предположим, что молния весила 1 грамм. Подсчет прост. Какова должна была быть температура тела массой 1 грамм, чтобы оно могло нагреть 20 литров воды с 10 до 100 градусов и испарить 4 литра воды? Расчеты тоже просты. Но тем неожиданней результат. Оказывается, температура такого тела должна составлять несколько миллионов градусов!

Задание 1 № 38786 Укажите варианты ответов, в которых даны верные характеристики фрагмента текста. Запишите номера этих ответов.

1) Типичным признаком научной речи является в тексте наличие вводных слов и словосочетаний, содержащих указание на источник сообщения, порядок оформления мысли, предположение или уверенность в содержании высказываемого (таким образом, следовательно, предположим и др.)
2) Экспрессивность текста усиливает воздействие на читателя, слушателя и достигается за счет использования оценочных слов и выражений, как явных, так и неявных, привлекающих внимание заголовков и иных выносных элементов текста.
3) В тексте рассказывается о событиях в их временной последовательности, сообщается о последовательно сменяющих друг друга действиях, поэтому можно определить данный текст как текстповествование.
4) Для научных текстов характерно выяснение причинно-следственных отношений между явлениями, поэтому в них преобладают сложные предложения с различными типами союзов и союзных слов (пока, причем, который и др.).
5) Для текста характерны термины — слова, раскрывающие научные понятия.

Ответ: 145

Задание 2 № 38787 Самостоятельно подберите указательное местоимение, которое должно стоять на месте пропуска во втором предложении текста. Запишите это местоимение.

Ответ: такой

Задание 3 № 38788 Прочитайте фрагмент словарной статьи, в которой приводятся значения слова, выделенного в первом предложении текста. Определите значение, в котором это слово употреблено в тексте. Выпишите цифру, соответствующую этому значению в приведённом фрагменте словарной статьи. ОБРАЗОВАНИЕ

1) То, что образовалось как результат роста, каких-либо действий. Образование на коже. Жировое образование.
2) Получение систематизированных знаний и навыков, обучение, просвещение. П раво на образование. Народное образование.
3) Совокупность знаний, полученных в результате обучения. Дать образование кому-нибудь. Получить образование Начальное, среднее, высшее, специальное образование.
4) Отрасль экономики, хозяйства страны, объединяющая организации, учреждения, предприятия, занятые обучением, воспитанием, передачей знаний, выпуском учебной литературы, подготовкой учительских кадров. Министерство образования.
5) То же, что происхождение. Образование семьи. Образование жизни на планете.

Ответ: 1

Задание 4 № 153 В одном из приведённых ниже слов допущена ошибка в постановке ударения: НЕВЕРНО выделена буква, обозначающая ударный гласный звук. Выпишите это слово. молЯщий, нажИвший, завИдно, отогналА, крЕмень.

Ответ: кремень

Задание 5 № 4899 В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте лексическую ошибку, подобрав к выделенному слову пароним. Запишите подобранное слово. Будущий писатель рос в БЕДНОТЕ. После конференции состоялся конструктивный и ДРУЖЕСТВЕННЫЙ диалог с руководителями страны. К полудню ветер уже разогнал ДЫМОВУЮ завесу. На уроках мы совершали ЭКСКУРСЫ в историю русского языка.

Ответ: бедности

Задание 6 № 12855 Отредактируйте предложение: исправьте лексическую ошибку, исключив лишнее слово. Выпишите это слово. Можно говорить о разных типах молодёжных театров, среди них – традиционный реалистический театр (тяготеющий к психологической драме), театр на основе народного фольклора, игровой праздничный театр, театр абсурда.

Ответ: народного

Задание 7 № 6866 В одном из выделенных ниже слов допущена ошибка в образовании формы слова. Исправьте ошибку и запишите слово правильно.

МЛЕКОПИТАЮЩИЕСЯ животные
ЛЕГЧАЙШЕЕ пёрышко
ВЫЗДОРОВЕЮ
много БРЫЗГ
ЕДКИЙ аэрозоль

Ответ: млекопитающие

Задание 9 № 30130 Укажите варианты ответов, в которых во всех словах одного ряда содержится безударная чередующаяся гласная корня. Запишите номера ответов.

1) содержимое, водоросли, сочетаемость
2) поднимая (тяжести), запирать (дверь), почитать (старших)
3) перескочить, запросить (документы), теребить (платок)
4) загорелись (глаза), приращение, разжимать
5) возвращает (долги), озарение, косые (лучи солнца)

Ответ: 24

Задание 10 № 14572 Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.

1) не..хваченный (переписью), р..зместить, п..дметать;
2) раз..ёмный, под..ём, об..ект;
3) не..жатый, бе..дорожье, бе..заботно;
4) под..скать, сверх..нтересный, вз..мать;
5) пр..обретатель, пр..чудливый, пр..ходящий (домой).

Ответ: 25

Задание 11 № 14655 Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.

1) успока..вая, врем..ни
2) ноздр..ватый, француж..нка
3) преодол..вающий, горл..нка
4) локт..вой, желт..зна
5) недоум..вать, утр..чко

Ответ: 25

Задание 12 № 14509 Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.

1) зате..ла, выздоров..ть
2) отча..ться, разве..в
3) (друг) уступ..т, (слово) молв..тся
4) (учитель) провер..т, ляж..шь (пораньше)
5) пен..щееся, разбавл..нный

Ответ: 23

Задание 13 № 1196 Определите предложение, в котором НЕ со словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. Луна (не)бледна, а прозрачна, как хрусталь. Он ниоткуда (не)получал писем. (Не)исследованные места влекут меня, а глухие дебри. Дорога (не)ровная, зато самая короткая. Часовой пропустил их, (не)проверив пароля.

Ответ: неровная

Задание 14 № 2926 Определите предложение, в котором оба выделенных слова пишутся СЛИТНО. Раскройте скобки и выпишите эти два слова. ЧТО (БЫ) разжечь костер, требовалось топливо, но и вокруг нас, и (В) ДАЛИ была лишь голая степь. В пятницу мы обработали (В) ДВОЕ больше заявок, чем обычно, однако часть работы всё равно пришлось взять (НА) ДОМ. (В) ТЕЧЕНИЕ дня шторм не стихал, (ПО) ЭТОМУ катерам запрещено было выходить из бухты. Имейте (В) ВИДУ, что ваша шалость ВРЯД (ЛИ) легко сойдёт вам с рук. (ПО)СКОЛЬКУ утро было теплым, мы решили ТАК(ЖЕ), как и вчера, пройтись по набережной.

Ответ: чтобы вдали

Задание 15 № 6049 Укажите все цифры, на месте которых пишется НН. Цифры укажите в порядке возрастания. Груня глядела в маленькое, криво прорубле(1)ое окошко, прижавшись сморще(2)ым лбом к нестрога(3)ому переплёту око(4)ой рамы.

Ответ: 124

Задание 16 № 12486 Расставьте знаки препинания. Укажите предложения, в которых нужно поставить ОДНУ запятую. Запишите номера этих предложений. 1) Поздравить юбиляра пришли его родственники и коллеги и многочисленные друзья. 2) Герой-романтик находит равное себе начало лишь в общении со стихией: с миром океана или моря гор или прибрежных скал. 3) В отрывке из «Антоновских яблок» Бунина ощущается не столько желание автора быть помещиком сколько стремление быть свободным от мелочных дел. 4) Постоянное движение устремлённость к иным пределам составляет суть творческой жизни и как раз об этом написал Пастернак в одном из стихотворений. 5) Утром восток загорелся румянцем и мелкие облачка окрасились в нежный цвет.

Ответ: 23

Задание 17 № 12793 Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Будто (1) окружённый синим воздухом (2) он быстро приближался (3) по привычке своей торопливо и шумно влетая (4) в класс (5) и потом долго и увлечённо говорил.

Ответ: 235

Задание 18 № 477 Расставьте все недостающие знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Наша (1)ветхая лачужка (2) И печальна и темна. Что же ты(3) моя старушка(4) Приумолкла у окна? Или бури завываньем Ты(5) мой друг(6)утомлена, Или дремлешь под жужжаньем Своего веретена? Выпьем(7) добрая подружка(8) Бедной юности моей(9) Выпьем с горя; где же (10)кружка? Сердцу будет веселей. (А. С. Пушкин)

Ответ: 345679

Задание 19 № 5117 Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Организму человека (1) необходимы микроэлементы (2) использование (3) которых (4) в комплексных удобрениях (5) увеличивает питательную ценность плодов и овощей.

Ответ: 2

Задание 20 № 2002 Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Зрители замерли в ожидании (1) и (2) когда занавес медленно поднялся (3) и показались великолепные декорации (4) в зале послышались восхищённые возгласы.

Ответ: 124

Задание 21 № 14968 Найдите предложения, в которых запятые ставятся в соответствии с одним и тем же правилом пунктуации. Запишите номера этих предложений. (1)Чудско-Псковское озеро, будучи третьим по величине на территории Европы, представляет собой озёрный комплекс. (2)Этот комплекс, расположенный на границе Ленинградской и Псковской областей и Эстонии, состоит из трёх частей. (3)Их иногда называют отдельными озёрами: Псковское, Чудское, Среднее. (4)Общая длина комплекса составляет 150 километров, ширина— 50 километров, общая площадь поверхности— 3550 квадратных километров. (5)Общая глубина озера составляет 6 метров— оно мелководно. (6)География озера обширна: в него впадает более 30 рек, а вытекает только одна— Нарва. (7)Для него характерны болотистые низменные берега; местами можно встретить поросшие соснами холмы и дюны. (8)Самый крупный город, построенный на российском побережье Чудско-Псковского озера,— Гдов. (9)На Чудско-Псковском озере располагаются 29 островов (обитаем только один из них), 22 из которых находятся на территории Чудского озера.

Ответ: 28

Задание 22 № 13908 Какие из высказываний не соответствуют содержанию текста? Укажите номера ответов. Цифры укажите в порядке возрастания. Какие из высказываний не соответствуют содержанию текста? Укажите номера ответов. 1) Детство рассказчика прошло в получасе езды от Иркутска, в деревне, расположенной на Ангаре. 2) В деревне, в которой жил рассказчик, люди отличались красноречием, даже болтливостью. 3) Когда рассказчик учился в Москве, он стремился избавиться от своего деревенского говора, чтобы соответствовать филологической выправке. 4) Первые писательские опыты рассказчика носили подражательный характер. 5) Рассказчика упрекали за то, что он якобы слишком активно, без меры, использует в своих произведениях родной сибирский диалект.

Ответ: 123

Задание 26 № 13912 «Образность распутинской речи, свойственная его художественным произведениям, нашла отражение и в публицистике этого автора. На уровне лексики следует отметить такой троп, как (А)______ (в предложениях 18, 34), а также такое средство, как (Б)______ (“на семи ветрах” в предложении 10, “не в ходу” в предложении 16). Стремясь донести до читателя свою мысль, В.Г. Распутин на протяжении всего текста использует и такое лексическое средство, как (В)______ (в предложениях 6, 9, 43). Встречается в тексте и такой синтаксический приём, как (Г)______ (в предложениях 4–5)».

Ответ: 9268

Задание 27 № 13887 Напишите сочинение по прочитанному тексту. Сформулируйте одну из проблем, поставленных автором текста. Прокомментируйте сформулированную проблему.

Другие тренировочные варианты ЕГЭ по русскому языку 11 класс:

Тренировочный вариант №210927 ЕГЭ 2022 по русскому языку 11 класс 100 баллов с ответами

23.09.2021 РЯ2110101 РЯ2110102 русский язык 11 класс ЕГЭ 2022 статград ответы и задания

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Задание 1

В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.

Ответ: 0,4

Скрыть

Задание 2

Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.

Ответ: 5

Скрыть

Задание 3

В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.

Ответ: 0,125

Скрыть

Задание 4

Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.

Ответ: 0,46

Скрыть

Задание 5

Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$

Ответ: -7

Скрыть

Задание 6

Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$

Ответ: -1

Скрыть

Задание 7

На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.

Ответ: 7

Скрыть

Задание 8

Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

Ответ: 1,8

Скрыть

Задание 9

Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Ответ: 11

Скрыть

Задание 10

На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.

Ответ: 0,25

Скрыть

Задание 11

Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$

Ответ: 17

Скрыть

Задание 12

а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$

б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].

Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$

Скрыть

Задание 13

Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.

а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.

б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.

Ответ: $$6sqrt{3}$$

Скрыть

Задание 14

Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$

Ответ: $$2;[log_{3}12;+infty)$$

Скрыть

Задание 15

15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:

— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;

— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;

— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.

Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.

Ответ: 13 млн. руб.

Скрыть

Задание 16

Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.

а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.

б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.

Ответ: $$frac{sqrt{6}}{2}$$

Скрыть

Задание 17

Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.

Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$

Скрыть

Задание 18

Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.

а) Может ли $$n$$ равняться 64?

б) Может ли $$n$$ равняться 78?

в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?

Ответ: а)да б)нет в)73

Скрыть

Источник

Решение и ответы заданий Варианта №6 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса.

Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание.
Решены те задания, у которых кнопка «Смотреть решение» зелёная.

Задание 1.
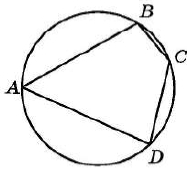
Точки А, B, С, D, расположенные на окружности, делят эту окружность на четыре дуги АВ, ВС, CD и AD, градусные величины которых относятся соответственно как 12:4:7:13. Найдите угол BAD. Ответ дайте в градусах.

Задание 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объём отсеченной треугольной призмы равен 4,5. Найдите объём исходной призмы.

Задание 3.
Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,06. В некотором городе из 1000 проданных блендеров в течение года в мастерские по гарантии поступило 54 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

Задание 4.
Вероятность того, что батарейка бракованная, равна 0,08. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Задание 5.
Решите уравнение log₂₇ 3^5–4x = 9.

Задание 6.
Найдите значение выражения frac{sqrt[4]{18}cdot sqrt[4]{27}}{sqrt[4]{6}}.

Задание 7.
Прямая y = 5x – 9 является касательной к графику функции y = 20x² – 15x + с. Найдите c.

Задание 8.
Мяч бросили под острым углом α к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле t=frac{2v_{0}sinalpha}{g}. При каком значении угла α (в градусах) время полёта составит 3 секунды, если мяч бросают с начальной скоростью v₀ = 30 м/с². Считайте, что ускорение свободного падения g = 10 м/с².

Задание 9.
Расстояние между пристанями А и В равно 140 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 52 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.

Задание 10.
На рисунке изображён график функции f(x) = a^x–2. Найдите значение x, при котором f(x) = 27.

Задание 11.
Найдите точку максимума функции y = x³ + 5,5x² – 42x + 18.

Задание 12.
а) Решите уравнение 750^{cos:3x}+6cdot 125^{frac{1}{3}+cos:3x}=5^{5cos:3x}+30^{1+cos:3x}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi}{4};-frac{3pi}{4}].

Задание 13.
В правильную треугольную пирамиду с боковым ребром 4 и стороной основания 2√3 вписан шар. Плоскость α перпендикулярна высоте пирамиды и проходит через её середину.

а) Докажите, что плоскость α и шар не имеют общих точек.
б) Найдите расстояние от центра шара до плоскости α.

Задание 14.
Решите неравенство frac{16–3^{x}}{log_{2}^{2}(x+1,5)–4}ge 0.

Задание 15.
В июне 2025 года Олег Вадимович планирует взять кредит в банке на 4 года. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 20 % от суммы долга на конец предыдущего года;
– в период с февраля по июнь каждого из 2026, 2027 и 2028 годов необходимо выплатить часть долга, причём каждый из платежей 2027 и 2028 годов в 1,6 раза больше платежа предыдущего года;
– в период с февраля по июнь 2029 года выплачивается оставшаяся сумма по кредиту, равная 1 770 240 рублей.
Найдите сумму кредита, если общие выплаты по нему составили 8 994 240 рублей.

Задание 16.
В трапеции ABCD с меньшим основанием BC точки E и F – середины сторон BC и AD соответственно. В каждый из четырехугольников ABEF и ECDF можно вписать окружность.

а) Докажите, что трапеция ABCD равнобедренная.
б) Найдите радиус окружности, описанной около трапеции ABCD, если ВС = 16, а радиус окружности, вписанной в четырехугольник ABEF, равен 7.

Задание 17.
Найдите все значения a , при каждом из которых система уравнений

begin{cases} y^{2}-x=2a+8, \ y^{4}+x^{2}=a^{2}-5a-6 end{cases}

имеет ровно четыре различных решения.

Задание 18.
Из k кг материала фабрика изготавливает n одинаковых деталей массой m кг каждая, причем k = nm + q, где q кг – остатки материала, и q < m. После внедрения новых технологий на фабрике начали выпускать детали нового типа, каждая из которых стала на 0,1 кг легче детали старого типа, причем из 18 кг материала деталей нового типа стали делать на две больше, чем делали деталей старого типа из 21 кг материала.

а) Может ли новая деталь весить столько, что на изготовление 50 новых деталей будет достаточно 18 кг материала, а на 51 – уже нет?
б) Может ли новая деталь весить столько, что на изготовление 36 новых деталей будет достаточно 18 кг материала, а на 37 – уже нет?
в) Найдите все такие числа n, что фабрика может выпускать n новых деталей из 25 кг материала, не нарушая условия q < m.

Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.3 / 5. Количество оценок: 3

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник