Задания
Версия для печати и копирования в MS Word
Тип 4 № 509088
Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс.
У Маши уже есть восемь разных принцесс из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 1 или 2 шоколадных яйца?
Аналоги к заданию № 509078: 509081 509079 509080 509082 509083 509084 509085 509086 509087 509088 Все
Прототип задания
·
·
Курс Д. Д. Гущина
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Спрятать решение
Решение.
Введём обозначения углов, как показано на рисунке. Пусть R — длина половины диагонали. В силу связи основных углов в правильной пирамиде:
поэтому
Ответ: 11.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
Задания
Версия для печати и копирования в MS Word
Тип 17 № 2949
Найдите корень уравнения
Решение.
Это задание ещё не решено, приводим решение прототипа.
Найдите корень уравнения
Перейдем к одному основанию степени:
Ответ: 12,5.
Аналоги к заданию № 26655: 2995 518397 518425 518445 518469 2949 2951 2953 2955 2957 … Все
Задание 1320
Найдите все значения параметра а, при каждом из которых система имеет единственное решение:
$$left{begin{matrix}( x-1 )( x+2 )leqslant 0, 8x^{2}+8y^{2}-16a ( x-y ) + 15a^{2}-48y-50a+72=0end{matrix}right.$$
Ответ: $$-frac{16}{7};-2;0;2$$
Задание 1321
Найдите все значения $$a$$, при каждом из которых наибольшее значение функции $$f(x)= |x-a|-x^{2}$$ не меньше 1
Ответ: $$(-infty;-frac{3}{4} ]cup [frac{3}{4};+infty )$$
Задание 1322
Найдите все значения $$a$$, при каждом из которых наименьшее значение функции $$f(x)=4ax+|x^{2}+6x+5|$$ больше, чем -24
Ответ: $$left ( frac{3-sqrt{29}}{2};frac{3+sqrt{29}}{2} right )$$
Задание 1323
Найдите все значения $$a$$, при каждом из которых наименьшее значение функции $$f(x)=4x^{2}+4ax+a^{2}-2a+2$$ на множестве $$|x|geqslant 1$$ не менее 6
Ответ: $$aleq -2 ; a = 0$$
Задание 1324
Найдите все значения $$a$$, при каждом из которых функция $$f(x)=x^{2}-2|x-a^{2}|-8x$$ имеет более двух точек экстремума
Ответ: $$(-sqrt{5};-sqrt{3})cup (sqrt{3};sqrt{5})$$
Задание 1325
Найдите все значения $$a$$, при каждом из которых функция $$f(x)=x^{2}-2|x-a^{2}|-4x$$ имеет хотя бы одну точку максимума
Ответ: $$(-sqrt{3};-1)cup (1;sqrt{3})$$
Задание 1326
Найдите все значения параметра $$a$$, при каждом из которых среди значений функции $$y=frac{x^{2}-2x+a}{6+x^{2}}$$ есть ровно одно целое число
Ответ: $$(1 ; 11)$$
Задание 1327
Найдите все значения $$a$$, при каждом из которых график функции $$f(x)=x^{2}-3x+2-|x^{2}-5x+4|-a$$
Ответ: $$(-infty ;-2]cup [0;+infty)$$
Задание 1328
Найдите все значения параметра $$a$$, при каждом из которых множество значений функции $$y=frac{a+3x-ax}{x^{2}+2ax+a^{2}+1}$$ содержит отрезок $$[0;1]$$
Ответ: $$left(-infty;frac{7-2sqrt{6}}{5}right]cup left[frac{7+2sqrt{6}}{5};3right)cup left(3;+inftyright)$$
Задание 1329
Найдите все такие значения параметра $$a$$, при каждом из которых уравнение $$(4x-x^{2})^{2}-32sqrt{4x-x^{2}}=a^{2}-14a$$ имеет хотя бы одно решение
Ответ: $$[0;6]cup [8;14]$$
Задание 2503
Найдите все а, при каждом из которых уравнение имеет ровно один корень: $$left|x-2right|+left|xright|-ax=2(a-1)$$
Ответ: $$(-infty ;-2)cup$$ {1}$$cup [2;infty )$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2949
Найдите все значения параметра b, при которых система $$ left{begin{matrix}x=-|b-y^{2}| y=a(x+b^{2})end{matrix}right.$$ имеет решение при любом значении параметра а.
Ответ: $$left ( -infty ;-1 right ]cup left [ 0 ; +infty right )$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3039
При каких значениях параметра a среди решений неравенства $$log_{2}(x-100)-log_{frac{1}{2}}frac{|x-101|}{105-x}+log_{2}frac{|x-103|(105-x)}{x-100}> a$$ содержится единственное целое число?
Ответ: $$[0;log_{2}3)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3163
Найдите все а, при каждом из которых уравнение $$3*2^{x+1}+frac{3}{2^{x-1}}+a(18-x^{2})=6(a^{2}+2)$$ имеет ровно одно решение
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3209
Найдите все значения а, при каждом из которых неравенство $$frac{a^{2}-4x-5}{x^{2}-4x-5}geq1$$ имеет ровно четыре целочисленных решения. Для каждого такого a укажите эти решения.
Ответ: в видео
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Джинни и Джорджия 1-2 сезон смотреть онлайн
После смерти своего мужа 30 летняя женщина Джорджия Миллер решает начать жизнь с чистого листа. Поэтому она решает переехать в Новую Англию вместе со своими детьми, дочерью Джинни и сыном Остином. Устав от многочисленных переездов, дети искренне желают наконец-то осесть на одном месте и жить, не оглядываясь на прошлое своей матери. Джорджия из-за своих прошлых ошибок вынуждена постоянно менять место жительство. Разный взгляд на будущее приводит к разногласиям и конфликтам между женщиной и её детьми. Несмотря на все неурядицы, Новая Англия понравилась Джинни некоторыми перспективами, поскольку именно здесь юной девушке представилась возможность учиться в элитной школе и общаться с интересными людьми.
Поскольку Джорджия совершила большое количество ошибок в прошлом, она всячески стремится оградить детей от необдуманных поступков и решений. Несмотря на это, женщина до сих пор считает себя молодой девушкой. Поэтому она желает найти того единственного мужчину, с которым она смогла бы прожить всю свою жизнь. Такое легкомысленное поведение матери пугает Джинни, ведь Джорджия всё больше времени, сил и внимания уделяет новым ухажёрам. К каким последствиям приведёт такое поведение женщины?
- Оригинальное название: Ginny & Georgia
- Год выхода: 2021
- Страна: США
- Премьера: 24 февраля 2021
- Режиссер: Аня Адамс, Каталина Агиляр Мастретта, Renuka Jeyapalan
- Перевод: TVShows
- Качество: FHD (1080p)
- Статус сериала: На паузе
-
7.5
7.4
- Актеры: Брианна Хоуи, Антония Джентри, Дизель Ла Торрака, Дженнифер Робертсон, Феликс Маллард, Сара Вайсгласс, Скотт Портер, Реймонд Эблэк, Mason Temple, Кэти Дуглас
- Канал: Netflix
- Жанр: Драма, Комедия
«Джинни и Джорджия» смотреть онлайн бесплатно в хорошем качестве
Смотреть онлайн
Плеер 2
Трейлер
Свет
Добавить в закладки
Подписывайтесь на нашу группу в VK
Permalink
Cannot retrieve contributors at this time
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| # Задача №2949. Обмен значений | |
| # Напишите программу, которая считывает значения двух целочисленных переменных a и b, | |
| # затем меняет их значения местами (то есть в переменной a должно быть записано то, что раньше хранилось в b, | |
| # а в переменной b записано то, что раньше хранилось в a). Затем выведите значения переменных. | |
| # | |
| # Входные данные | |
| # Вводятся целые числа a и b. | |
| # | |
| # Выходные данные | |
| # Выведите ответ на задачу. | |
| # | |
| # Примечание | |
| # Решением задачи не является такой код: | |
| # | |
| # a = input () | |
| # b = input () | |
| # print (b, a) | |
| # То есть ваша программа должна иметь примерно такой вид: | |
| # a = input () | |
| # b = input () | |
| # # Допишите сюда | |
| # # свой код | |
| # print (a, b) | |
| # | |
| # Примеры | |
| # входные данные | |
| # 8 | |
| # 5 | |
| # выходные данные | |
| # 5 8 | |
| a = int(input()) | |
| b = int(input()) | |
| a += b | |
| b = a — b | |
| a = a — b | |
| print(a, b) |
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
Зарегистрирован: 10 июн 2010, 15:00 |
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
Зарегистрирован: 06 май 2012, 21:09 |
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
Зарегистрирован: 18 ноя 2015, 07:49 |
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.
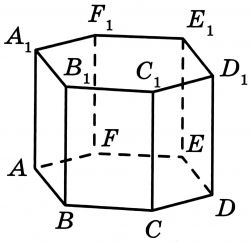
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac19right)^{x+4}=729)
Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)
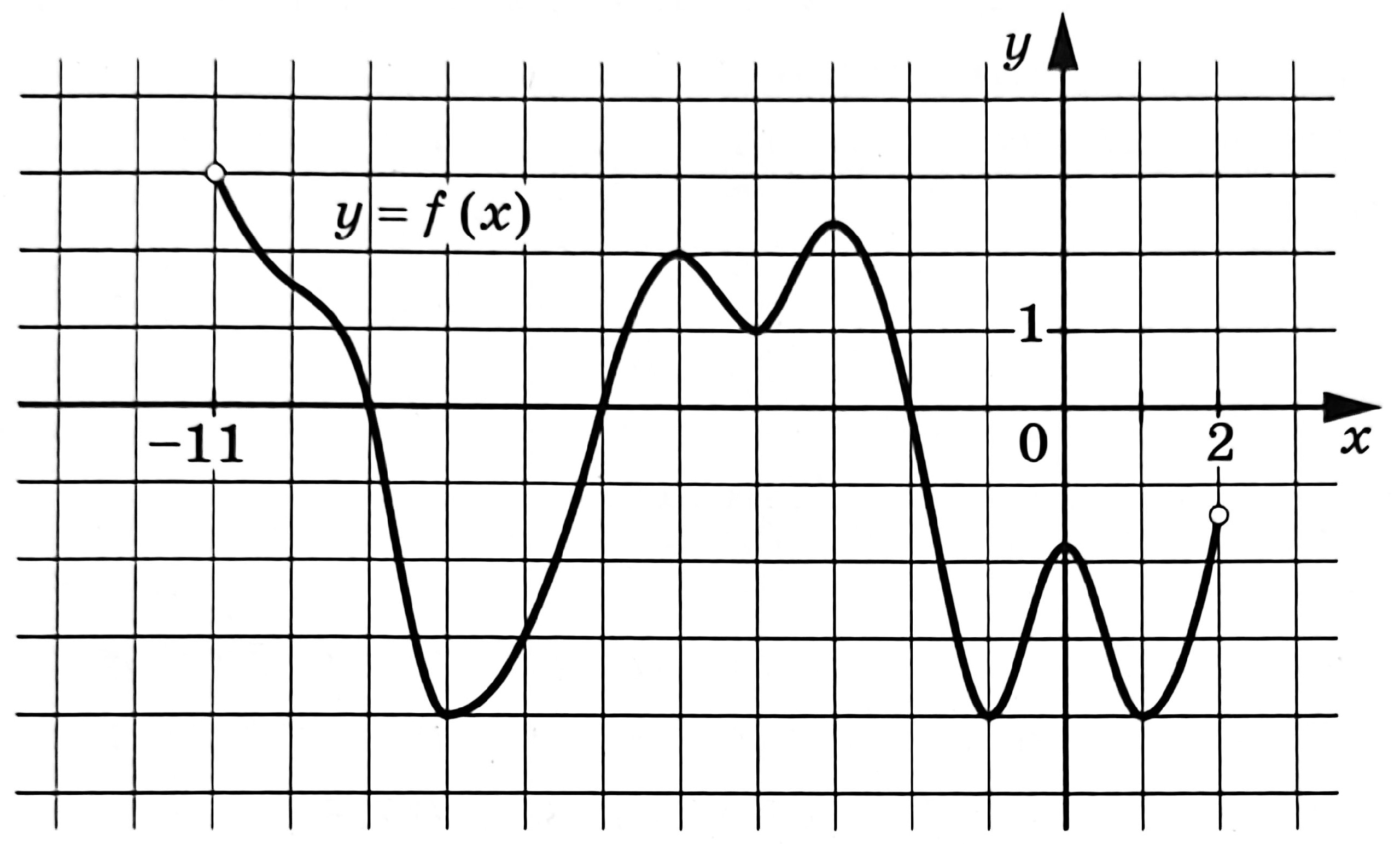
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
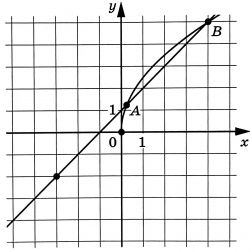
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.
Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])
а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Неотрицательное
шестизначное
число 509088
.
Произведение всех цифр числа: 0.
Делители числа 509088: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96, 5303, 10606, 15909, 21212, 31818, 42424, 63636, 84848, 127272, 169696, 254544, 509088.
1336608 — сумма делителей.
509088 и 0.0000019642969388396503 являются взаимно обратными числами.
Данное число можно представить произведением: 2 * 2 * 2 * 2 * 2 * 3 * 5303.
Другие представления числа 509088:
двоичная система счисления: 1111100010010100000, троичная система счисления: 221212100010, восьмеричная система счисления: 1742240, шестнадцатеричная система счисления: 7C4A0.
Количество информации в числе байт 509088 это 497 килобайтов 160 байтов .
Азбука Морзе для числа 509088: ….. —— —-. —— —.. —..
Число не является числом Фибоначчи.
Косинус 509088: 0.6922, синус 509088: -0.7218, тангенс 509088: -1.0428.
Число 509088 имеет натуральный логарифм: 13.1404.
Десятичный логарифм: 5.7068.
713.5040 — квадратный корень из числа, 79.8480 — корень кубический.
Квадрат числа: 2.5917e+11.
Число 509088 в секундах это 5 дней 21 час 24 минуты 48 секунд .
В нумерологии число 509088 означает цифру 3.
Канал видеоролика: Ломоносов клуб
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #подготовкакогэ #ответы_огэ #подготовкакегэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

1 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб

2 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб

3 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб

4 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
08.12.2022
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Скрыть
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Скрыть
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Скрыть
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Скрыть
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Скрыть
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
Скрыть
Задание 10
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Скрыть