Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.
Спрятать решение
Решение.
Боковые грани исходной призмы вдвое больше соответствующих боковых граней отсеченной призмы, поэтому площадь боковой поверхности исходной призмы равна 86.
Источник: ЕГЭ по математике — 2015. Досрочная волна, вариант ФИПИ

Пробный вариант составлен на основе официальной демоверсии от ФИПИ за 2023 год.
В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.
Скачать тренировочный вариант ЕГЭ: Скачать
Интересные задания
1. На окружности отмечены точки 𝐴, 𝐵 и 𝐶. Дуга окружности 𝐴𝐶, не содержащая точку 𝐵, составляет 200°. Дуга окружности 𝐵𝐶, не содержащая точку 𝐴, составляет 80°. Найдите вписанный угол 𝐴𝐶𝐵. Ответ дайте в градусах.
3. В сборнике билетов по математике всего 20 билетов, в 16 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам.
4. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,06. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля
9. Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов одиннадцать таких же рубашек дороже куртки?
15. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года) и банку будет выплачено 311 040 рублей?
16. Биссектриса 𝐵𝐵1 и высота 𝐶𝐶1 треугольника 𝐴𝐵𝐶 пересекают описанную окружность в точках 𝑀 и 𝑁. Известно, что угол 𝐵𝐶𝐴 равен 85° и угол 𝐴𝐵𝐶 равен 40°.
а) Докажите, что 𝐶𝑁 = 𝐵𝑀.
б) Пусть 𝑀𝑁 и 𝐵𝐶 пересекаются в точке 𝐷. Найти площадь треугольника 𝐵𝐷𝑁, если его высота 𝐵𝐻 равна 7.
Вам будет интересно:
Тренировочные 4 варианта с ответами ЕГЭ 2023 по русскому языку в новом формате
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Натуральное вещественное
шестизначное
число 509198
является составным.
Произведение цифр: 0.
8 — количество делителей.
Их сумма: 780192.
Обратным числом является 0.000001963872599656715.
Данное число представляется произведением: 2 * 47 * 5417.
Представления числа:
двоичная система счисления: 1111100010100001110, троичная система счисления: 221212111012, восьмеричная система счисления: 1742416, шестнадцатеричная система счисления: 7C50E.
497 килобайтов 270 байтов — столько информации находится в числе байт 509198.
В виде кода азбуки Морзе: ….. —— —-. .—- —-. —..
Синус числа: 0.6904, косинус числа: -0.7234, тангенс числа: -0.9544.
Натуральный логарифм равен 13.1406.
Логарифм десятичный равен 5.7069.
713.5811 — квадратный корень, 79.8538 — кубический корень.
Число секунд 509198 – это 5 дней 21 час 26 минут 38 секунд .
Нумерологическая цифра этого числа — 5.
Новый тренировочный вариант №41054182 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
скачать вариант ЕГЭ 2022
скачать ответы и решения
Решу ЕГЭ 2022 по математике профиль тренировочный вариант №41054182
Ответы и решения для варианта:
Задание 2 решу ЕГЭ № 1001 На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Ответ: 0,95
Задание 3 решу ЕГЭ № 27913 Сторона ромба равна 1, острый угол равен 30 градусов. Найдите радиус вписанной окружности этого ромба.
Ответ: 0,25
Задание 6 решу ЕГЭ № 515183 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
Ответ: 5
Задание 8 решу ЕГЭ № 99595 Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Ответ: 12
Задание 10 решу ЕГЭ № 320177 Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства— яйца высшей категории, а из второго хозяйства— 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Ответ: 0,75
Задание 13 решу ЕГЭ № 514655 В основании прямой треугольной призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с прямым углом C, AC = 4, BC = 16, Точка Q — середина ребра A1B1 , а точка P делит ребро B1C1 в отношении 1:2, считая от вершины C1 . Плоскость APQ пересекает ребро CC1 в точке M. а) Докажите, что точка M является серединой ребра CC1 . б) Найдите расстояние от точки A1 до плоскости APQ.
Задание 15 решу ЕГЭ № 513923 В июле 2016 года планируется взять кредит в размере 4,2 млн. руб. Условия возврата таковы: — каждый январь долг возрастает на r% по сравнению с концом предыдущего года. — с февраля по июнь необходимо выплатить часть долга. — в июле 2017, 2018 и 2019 годов долг остается равным 4,2 млн. руб. — суммы выплат 2020 и 2021 годов равны. Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 6,1 млн. рублей.
Ответ: 10
Задание 16 решу ЕГЭ № 509467 В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 12, BC = 5. Окружность радиуса с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности. а) Докажите, что радиус второй окружности меньше, чем длины катета AC. б) Найдите радиус второй окружности.
Ответ: 2
Задание 18 решу ЕГЭ № 505503 а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр? б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр? в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.
Ответ: а) да; б) нет; в) 110.
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Свойства числа 509198
| Множители | 2 * 47 * 5417 | |
| Делители | 1, 2, 47, 94, 5417, 10834, 254599, 509198 | |
| Количество делителей | 8 | |
| Сумма делителей | 780192 | |
| Предыдущее целое | 509197 | |
| Следующее целое | 509199 | |
| Простое число? | NO | |
| Предыдущее простое | 509149 | |
| Следующее простое | 509203 | |
| 509198th простое число | 7515047 | |
| Является числом Фибоначчи? | NO | |
| Число Белла? | NO | |
| Число Каталана? | NO | |
| Факториал? | NO | |
| Регулярное число? | NO | |
| Совершенное число? | NO | |
| Полигональное число (s < 11)? | NO | |
| Двоичное | 1111100010100001110 | |
| Восьмеричная | 1742416 | |
| Двенадцатеричный | 206812 | |
| Шестнадцатиричная | 7c50e | |
| Квадрат | 259282603204 | |
| Квадратный корень | 713.58110961544 | |
| Натуральный логарифм | 13.140592217928 | |
| Десятичный логарифм | 5.7068866891869 | |
| Синус | 0.69042167672652 | |
| Косинус | -0.72340715251243 | |
| Тангенс | -0.95440261314622 |
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2023
numberempire.com
Все права защищены
Задание 1
Альбом для рисования стоит 30 рублей. Какое наибольшее число таких альбомов можно будет купить на 500 рублей во время акции, где на все канцтовары действует скидка 15%?
Ответ: 19
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Скидка действует 15%, значит заплатить придется 100-15=85% от основной суммы: 30 — 100% x — 85% x = 30 * 85 / 100 = 25.5 2) 500/25.5=19.6 ( если округлить ) , значит можно купить 19 тетрадей
Задание 2
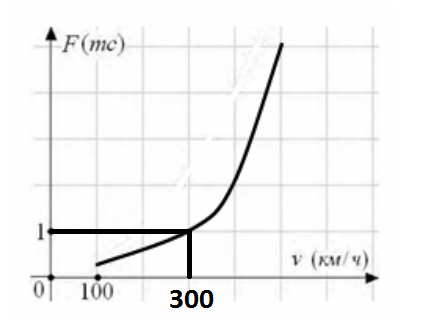
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 300 км/ч?
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
На рисунке видно, что подъемная сила в данном случае будет равна 1
Задание 3
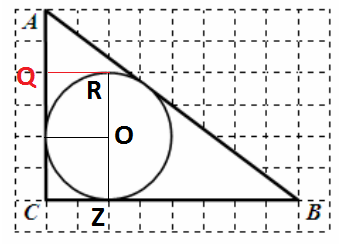
Найдите радиус окружности, вписанной в треугольник АВС, если размер клетки 1 см х 1 см. Ответ дайте в сантиметрах.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1 Вариант
Находим диаметр — RZ, он равен QZ = 4 . Значит радиус вписанной равен 2
2 Вариант
По теореме Пифаогора найдем AB = 10
Найдем полупериметр $$p = frac{10+8+6}{2}=12$$
Найдем площадь через половину произведения катетов $$S = frac{1}{2}6*8=24$$
Найдем радиус вписанной окружности $$ r = frac{S}{p}=frac{24}{12}=2$$
Задание 4
В супермаркете стоят три банкомата. Каждый из них может быть неисправен с вероятностью 0,2 независимо от других. Найдите вероятность того, что в супермаркете ровно два банкомата окажутся в рабочем состоянии .
Ответ: 0.384
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Вероятность того, что банкомат окажется в рабочем состоянии, противоположна нерабочему состоянию, а значит равна 1 — 0,2 = 0,8
Так как у нас независимо друг от друга вероятности банкоматов существуют, то вероятность того, что два исправны выглядит так ( И — исправен, Н — неисправен, 1,2,3 — номера банкоматов ):
| 1 | 2 | 3 | вероятность |
| И | И | Н | 0,8*0,8*0,2=0,128 |
| И | Н | И | 0,8*0,2*0,8=0,128 |
| Н | И | И | 0,2*0,8*0,8=0,128 |
Следовательно, конечная вероятность равна сумме полученных: 0.128 * 3 = 0.384
Задание 5
В прямоугольном треугольнике АВС угол С – прямой. СН – высота, СL – биссектриса, ∠ А = 39. Найдите ∠ НСL. Ответ дайте в градусах.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как CH — высота, то треугольники ACH и CBH подобны, а значит ∠HCB=∠CAH=39
В таком случае ∠ACH = 90 — ∠HCB = 90 — 39 = 51
∠ ACL = 90 / 2 = 45 ( так как CL биссектриса )
Тогда ∠LCH = ∠ACH — ∠ACL = 51 — 45 = 6
Задание 6
На рисунке приведен график f ‘ (x) – производной функции у = f (x). Определите абсциссу точки графика функции у = f (x), в которой касательная параллельна прямой у = 2х – 1 или совпадает с ней.
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как касательная к графику параллельна или совпадает с прямой y = 2x — 1, и при этом значение производной равно коэффициенту k линейной функции ( в нашем случае этот коэффициент равен 2 ), то и значение производной, которое мы ищем, равно 2. А так как нам дан график производной, то мы смело находим точку с ординатой (ось Оу) равную 2 и ищем абсциссу этой точки. Она равна -3
Задание 7
В кубе с ребром, равным 3, сделано сквозное отверстие размером 1 х 1. Найдите площадь полной поверхности полученного многогранника.
Ответ: 64
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь поверхности самого куба равна 3*3*6=54. Из него вычитаем два окошка , каждое из которых 1*1 = 1. То есть остается 54 — 2 = 52.
Но так же надо прибавить площади появившихся граней внутри куба. Каждая из них прямоугольник со сторонами 3 и 1 . Значит площадь 3*1=3. Их 4 штуки, а значит 3*1*4=12
В итоге площадь поверхности многогранника будет 52+12=64
Задание 8
Известно, что $$ tg x = frac{2}{sqrt{21}}$$ и $$pi < x< frac{3pi }{2}$$. Найдите sin x
Ответ: -0.4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Угол располагается в третьей четверти, поэтому sin будет отрицательный. Найдем сначала ctg x: $$ ctg x = frac {1}{tg x}= frac {1}{frac{2}{sqrt{21}}}=frac{sqrt{21}}{2}$$ Выразим sin x из формулы $$ 1 + ctg^{2} x = frac{1}{sin^{2} x} $$ $$ frac{1}{1 + ctg^{2} x} =sin^{2} x $$ $$sin x = — sqrt{ frac{1}{1 + ctg^{2} x} } $$ $$sin x = — sqrt{ frac{1}{1 + (frac{sqrt{21}}{2})^{2}} }=- sqrt{ frac{1}{1 + frac{21}{4}}}=-frac{2}{5}=-0.4 $$
Задание 9
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA= αρgr3, где α=4,2 – постоянная, r – радиус аппарата в метрах, ρ=1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g=10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим имеющиеся значения в формулу: $$336000=4.2*1000*10*r^{3}$$ $$r^{3}=frac{336000}{4.2*1000*10}=8$$ r = 2
Задание 10
Первые пять часов автомобиль ехал со скоростью 60 км/ч, следующие 246 км он преодолел за 3 часа, а последние 130 км проехал со скоростью 65 км/ч. Найдите среднюю скорость (в км/ч) автомобиля на всем пути.
Ответ: 67.6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
За первые пять часов он проехал 60 * 5 = 300 км
Последние 130 км он ехал $$frac{130}{65}=2$$ ч
Тогда средняя скорость будет равна $$frac{300+246+130}{5+3+2}=67.6$$
Задание 11
Найдите точку максимума функции $$f(x)=24-3x^{4}-8x{3}$$
Ответ: -2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную функции и приравняем ее к нулю:
$$f'(x)=-12x^{3}-24x^{2}=0$$
$$f'(x)=-12x^{2}(x+2)=0$$
Получаем или x = 0, или x = -2.
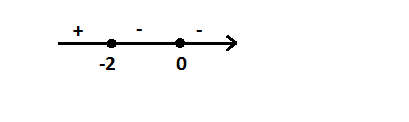
Отметим эти точки на координатной прямой и расставим знаки производной:
Как видим, точка максимум -2
Задание 12
Дано уравнение $$cos^{2}x(tg(frac{9pi}{2}+x)-3tg^{2}(pi-x))=cos 2x-1$$
А) Решите уравнение.
Б) Найдите его корни, принадлежащие промежутку $$[-4;-1]$$.
Ответ: А)$$-frac{pi}{4}+pi n,n in Z$$ Б)$$-frac{5pi}{4}$$
Задание 13
В основании прямой призмы $$ABCA_{1}B_{1}C_{1}$$ лежит равнобедренный треугольник $$ABC$$, в котором $$AB=AC$$.
А) Докажите, что объем пирамиды $$A_{1}BCC_{1}B_{1}$$ составляет 2/3 объема призмы.
Б) Найдите радиус сферы, описанной около пирамиды $$A_{1}BCC_{1}B_{1}$$, если известно, что $$AB=5$$, $$BC=6$$, $$AA_{1}=15$$.
Ответ: $$frac{65}{8}$$
Задание 14
Решите неравенство $$4cdotlog_{2}(8-2^{1+x^{2}})-log_{2}^{2}(2^{3-x^{2}}-2)leq 4x^{2}+3$$
Ответ: $$(-sqrt{2};-1];[1;sqrt{2})$$
Задание 15
В треугольнике $$ABC$$ проведена биссектриса $$BK$$ и на сторонах $$BA$$ и $$BC$$ взяты соответственно точки $$M$$ и $$P$$Р так, что $$angle AKM=angle CKP=frac{1}{2}angle ABC$$
а) Докажите, что прямая $$AC$$ касается окружности, описанной около треугольника $$MBP$$.
б) Найдите радиус окружности, описанной около треугольника $$MBP$$, если известно, что $$AB=10$$, $$BC=15$$, $$AC=20$$.
Ответ: $$frac{24sqrt{15}}{25}$$
Задание 16
1 мая 2017 г. Татьяна Константиновна положила 10 000 000 рублей в банк сроком на 1 год с ежемесячным начислением процентов и капитализацией под а % годовых. Это означает, что первого числа каждого месяца сумма вклада увеличивается на одно и то же количество процентов, рассчитанное таким образом, что за 12 месяцев она увеличится ровно на $$a$$ %. Найдите $$a$$, если известно, что через 6 месяцев сумма вклада Татьяны Константиновны составила 10 400 000 рублей.
Ответ: 8,16
Задание 17
Найдите все $$a$$, при каждом из которых система $$left{begin{matrix} y^2-2x^2+xy+9x-9=0\ ax^2+2ax-y-3+a=0 end{matrix}right.$$ имеет ровно четыре различных решения
Ответ: $$(-frac{1}{8};0);(0;frac{2}{9});(frac{2}{9};frac{1}{4})$$
Задание 18
Государство Новая Анчурия расположено на острове, имеющем форму круга. В стране 11 городов, расположенных на побережье. Каждый город напрямую соединен с каждым из остальных городов автотрассой.
А) Сколько автотрасс в государстве Новая Анчурия?
Б) После наводнения несколько автотрасс в стране закрыли на ремонт. Могло ли оказаться так, что теперь каждый город острова стал напрямую соединен автотрассой ровно с пятью другими городами?
В) Какое наибольшее число автотрасс в Новой Анчурии можно одновременно закрыть на ремонт, чтобы из каждого города можно было добраться на автомобиле до любого другого?
Ответ: А)55 Б)Нет В)45
Скрыть
а) Из каждого города выходит 10 дорог, поэтому всего есть 10 умножить на 11=110 концов дорог. Значит, дорог 55.
б) Если теперь из каждого города выходит 5 дорог, то всего есть 5 умножить на 11=55 концов дорог. Значит, дорог 27,5, что невозможно.
в) Можно оставить 10 дорог (например, соединяющих столицу со всеми городами, тогда откуда угодно куда угодно можно будет проехать через столицу), поэтому удастся закрыть 45.
Если оставить всего n-2 или меньше дорог на n городов, то это будет невозможно. В самом деле, у n-2 дорог 2n-4 конца, поэтому найдется город (на самом деле даже минимум 4 таких города) из которых выходит по одной дороге (0 дорог быть не может, из него тогда никуда нельзя доехать). Ясно, что проезжать транзитом через такой город нельзя. Поэтому если мысленно убрать с карты этот город и эту дорогу, на остальной карте можно будет проехать от любого города до любого другого. При этом число дорог снова на 2 меньше числа городов. Продолжая эти действия, придем к ситуации 0 дорог и 2 города, которая нам не подходит.