Решу егэ 509203

Информация о генераторе вариантов:

На данный момент в базе заданий 838 заданий (обновление было 20.09.2022) – только те, которые могут выпасть на экзамене. Варианты максимально приближены к вариантам реального ЕГЭ.

Источники заданий:

1) Прототипы из fipi.ru;
2) Прототипы из os.fipi.ru;
3) Прототипы с реальных ЕГЭ всех лет;
4) Прототипы с mathege.ru.
    На каждую позицию рандомно выпадает случайное задание из базы заданий.

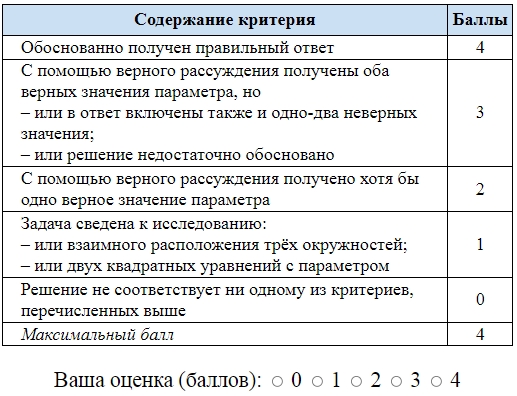
Описание каждой из позиций №1–18:

Задание 1. Планиметрия – все 160 прототипов темы, выпадающие на ЕГЭ.
 Задание 2. Стереометрия – все 183 прототипа темы, выпадающие на ЕГЭ.
Задание 3. Начала теории вероятностей – все 40 прототипов темы, выпадающие на ЕГЭ.
Задание 4. Вероятности сложных событий – все 37 прототипов темы, выпадающие на ЕГЭ. 
Задание 5. Простейшие уравнения – все 38 прототипов темы, выпадающие на ЕГЭ.
• Задание 6. Вычисления и преобразования – на данный момент 10 прототипов.
Задание 7. Производная и первообразная – все 44 прототипа темы, выпадающие на ЕГЭ.
Задание 8. Задачи с прикладным содержанием – все 71 прототип темы, выпадающие на ЕГЭ.
Задание 9. Текстовые задачи – все 93 прототипа темы, выпадающие на ЕГЭ.
Задание 10. Функции и их свойства – все 54 прототипа темы, выпадающие на ЕГЭ.
Задание 11. Наибольшее и наименьшее значение функции – все 54 прототипа темы, выпадающие на ЕГЭ.
    Условия прототипов заданий первой части взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)».

• Задание 12. Уравнения – на данный момент 10 прототипов.
• Задание 13. Стереометрическая задача – на данный момент 4 прототипа.
• Задание 14. Неравенства – на данный момент 10 прототипов.
• Задание 15. Финансовая математика – на данный момент 9 прототипов.
• Задание 16. Планиметрическая задача – на данный момент 4 прототипа.
• Задание 17. Задача с параметром – на данный момент 7 прототипов.
• Задание 18. Числа и их свойства – на данный момент 9 прототипов.

База заданий постоянно дополняется, в течение года будут добавлены все необходимые для подготовки прототипы.

Примеры заданий, тестовая часть.

Примеры заданий, развёрнутая часть.

На выполнение экзаменационной работы отводится 3 часа 55 минут.

Время выполнения варианта.

Тестовая часть проверяется автоматически, а развёрнутая часть самостоятельно вами по решениям и их критериям.

Пример критерия задания из развёрнутой части на 2 балла.

Пример задания из развёрнутой части на 4 балла.

В итоге выводится количество набранных баллов и ссылки на решения задач варианта:

Итог работы, ссылки на подробные решения всех задач.

Теги: тренировочные варианты, 11 класс, 2021, с ответами, новый вариант, профиль, пробный егэ.

Тренировочный вариант №20 в формате решу ЕГЭ 2023 по математике 11 класс профильный уровень от 27 января 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.

Скачать вариант с ответами

20вариант_егэ2023_профиль

Подробное решение каждого задания

решение_варианта_20

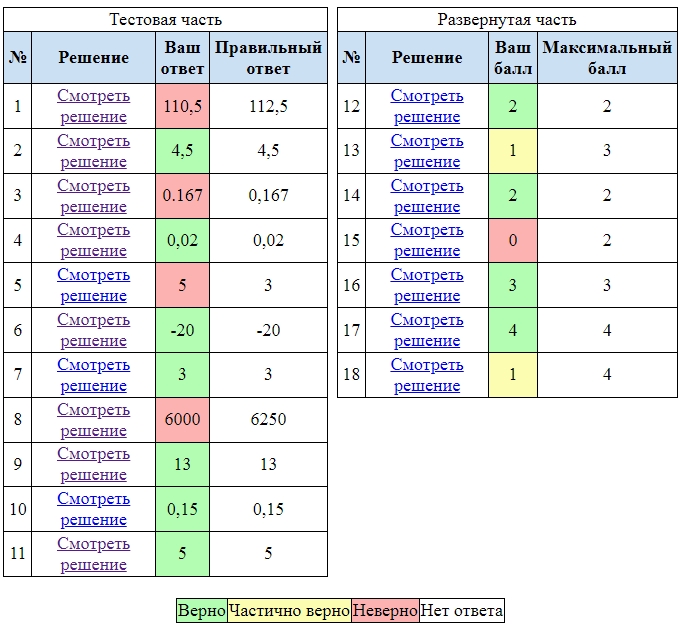
1. Периметр прямоугольной трапеции, описанной около окружности, равен 40, её большая боковая сторона равна 11. Найдите радиус окружности.

Ответ: 4,5

2. В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 найдите угол между прямыми 𝐶𝐷1 и 𝐴𝐷. Ответ дайте в градусах.

Ответ: 90

3. В классе 16 учащихся, среди них два друга – Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.

Ответ: 0,2

4. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,6. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,45. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Ответ: 0,27

7. На рисунке изображён график функции 𝑦 = 𝑓(𝑥), определённой на интервале (−9; 5). Найдите количество точек, в которых производная функции 𝑓(𝑥) равна 0.

Ответ: 9

9. Имеется два сосуда. Первый содержит 60 кг, а второй – 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 45% кислоты. Сколько процентов кислоты содержится в первом сосуде?

Ответ: 15

10. На рисунке изображены графики функций видов 𝑓(𝑥) = 𝑎√𝑥 и 𝑔(𝑥) = 𝑘𝑥, пересекающиеся в точках 𝐴 и 𝐵. Найдите абсциссу точки 𝐵.

Ответ: 36

Тренировочные варианты ЕГЭ 2023 математика база и профиль

11. Найдите точку минимума функции 𝑦 = 9𝑥 − 9 ∙ ln(𝑥 + 3) + 4.

Ответ: -2

13. В правильной четырёхугольной пирамиде 𝑆𝐴𝐵𝐶𝐷 сторона основания 𝐴𝐵 равна 4, а боковое ребро 𝑆𝐴 равно 7. На рёбрах 𝐶𝐷 и 𝑆𝐶 отмечены точки 𝑁 и 𝐾 соответственно, причём 𝐷𝑁: 𝑁𝐶 = 𝑆𝐾:𝐾𝐶 = 1: 3. Плоскость 𝛼 содержит прямую 𝐾𝑁 и параллельна прямой 𝐵𝐶. а) Докажите, что плоскость 𝛼 параллельна прямой 𝑆𝐴. б) Найдите угол между плоскостями 𝛼 и 𝑆𝐵𝐶.

14. Решите неравенство 2 log2 (1 − 2𝑥) − log2 ( 1 𝑥 − 2) ≤ log2 (4𝑥 2 + 6𝑥 − 1).

15. В июле 2016 года планируется взять кредит в банке в размере 𝑆 тыс. рублей, где 𝑆 − натуральное число, на 3 года. Условия его возврата таковы: – каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наименьшее значение 𝑆, при котором каждая из выплат будет составлять целое число тысяч рублей.

Ответ: 200

16. Около остроугольного треугольника 𝐴𝐵𝐶 с различными сторонами описали окружность с диаметром 𝐵𝑁. Высота 𝐵𝐻 пересекает эту окружность в точке 𝐾. а) Докажите, что 𝐴𝑁 = 𝐶𝐾. б) Найдите 𝐾𝑁, если ∠𝐵𝐴𝐶 = 35°, ∠𝐴𝐶𝐵 = 65°, а радиус окружности равен 12.

Ответ: 12

17. Найдите все значения 𝑎, при которых уравнение √𝑥 4 + (𝑎 − 5) 4 = |𝑥 + 𝑎 − 5| + |𝑥 − 𝑎 + 5| имеет единственное решение.

Ответ: {3; 7}

18. В ящике лежит 95 фруктов, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два фрукта различной массы, а средняя масса всех фруктов равна 100 г. Средняя масса фруктов, масса каждого из которых меньше 100 г, равна 73 грамма. Средняя масса фруктов, масса каждого из которых больше 100 г, равна 115 г. а) Могло ли в ящике оказаться поровну фруктов массой меньше 100 г и фруктов массой больше 100 г? б) Могло ли в ящике оказаться меньше 10 фруктов, масса каждого из которых равна 100 г? в) Какую наибольшую массу может иметь фрукт в этом ящике?

Ответ: а) нет б) нет в) 857

• Сборник Ященко ЕГЭ 2023 математика профильный уровень

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Целое неотрицательное
шестизначное

число 509203
– простое число.

Произведение цифр: 0.
У числа 2 делителя: 1, 509203.
И сумма этих делителей: 509204.
Обратное число для 509203 — это 0.0000019638533158681314.

Данное число можно представить произведением: 1 * 509203.

Представление числа в других системах счисления:
двоичный вид числа: 1111100010100010011, троичный вид числа: 221212111101, восьмеричный вид числа: 1742423, шестнадцатеричный вид числа: 7C513.
Если представить это число как набор байтов, то это 497 килобайтов 275 байтов .

В виде кода азбуки Морзе: ….. —— —-. ..— —— …—

Косинус числа: 0.4569, синус числа: 0.8895, тангенс числа: 1.9471.
У числа 509203 есть натуральный логарифм: 13.1406.
Число 509203 имеет десятичный логарифм: 5.7069.
713.5846 — квадратный корень из числа, 79.8541 — кубический корень.
Возведение в квадрат: 2.5929e+11.

Перевод из числа секунд — 5 дней 21 час 26 минут 43 секунды .
Нумерологическое цифра числа 509203 — 1.

Показана страница 1 из 14