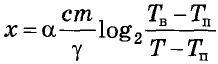цвет
Значения преобразования цвета
Здесь вы можете получить информацию о шестнадцатеричном, RGB, HSL, HSV, CMYK, XYZ, Yxy, CMY, десятичном, десятичном RGB, двоичном, Hunter Lab, CIE Lab, преобразовании цветов CIE Luv значения. Кроме того, вы можете найти примеры выбранного цветового кода для оттенков и оттенков, дополнительных, монохромных, дополнительных разделений, триадных, тетрадных, аналоговых, CMYK и RGB Percentage и HTML CSS.
Оттенки (Темные цвета)
Оттенки (Светлые цвета)
Дополнительный цвет
Монохроматический Цвета
Дополнительный сплит Цвета
Триады Цвета
тетрадный Цвета
Аналог Цвета
CMYK Percentage
Процент RGB
Предварительный просмотр и примеры CSS
Значения CSS RGBA
на белом фоне
на черном фоне
Белый текст включен Фон
ColorCodesLab.com — HEX, RGB, HSV, Hunter Lab, CIE Lab, CIE Luv, XYZ, Yxy, десятичный, десятичный RGB, двоичный, CMY, CMYK.
Черный текст включен Фон
ColorCodesLab.com — HEX, RGB, HSV, Hunter Lab, CIE Lab, CIE Luv, XYZ, Yxy, десятичный, десятичный RGB, двоичный, CMY, CMYK.
Граница с белым фоном
Граница на черном BG
Box Shadow
Внутренняя тень от коробки
Цвет текста
ColorCodesLab.com — HEX, RGB, HSV, Hunter Lab, CIE Lab, CIE Luv, XYZ, Yxy, десятичный, десятичный RGB, двоичный, CMY, CMYK.
Тень текста
ColorCodesLab.com — HEX, RGB, HSV, Hunter Lab, CIE Lab, CIE Luv, XYZ, Yxy, десятичный, десятичный RGB, двоичный, CMY, CMYK.
На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 509433?
На число 509433 без остатка (нацело) делятся следующие числа: 509433, 1018866, 1528299, 2037732, 2547165, 3056598, 3566031, 4075464, 4584897, 5094330, 5603763, 6113196 и многие другие.
Какие четные числа делятся на 509433?
На число 509433 делятся следующие четные числа: 1018866, 2037732, 3056598, 4075464, 5094330, 6113196, 7132062, 8150928, 9169794, 10188660, 11207526, 12226392 и многие други.
Какие нечетные числа делятся на 509433?
На число 509433 делятся следующие нечетные числа: 509433, 1528299, 2547165, 3566031, 4584897, 5603763, 6622629, 7641495, 8660361, 9679227, 10698093, 11716959 и многие другие.
На какое наибольшее число делится число 509433 без остатка?
Наибольшее число на которое делится число 509433 есть само число 509433. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 509433 без остатка, не считая числа 509433 и 1?
Наибольшим делителем числа 509433 не считая самого числа 509433 является число 169811.
Какое наименьшее натуральное число делится на 509433?
Наименьшее натуральное число которое делиться на число 509433 является само число 509433.
На какое наименьшее натуральное число делится число 509433?
Наименьшее натуральное число на которое можно разделить число 509433 — это число 1.
Делители числа 509433.
(что бы не забыть запишите все делители числа 509433 в блокнот.)На какие целые и(или) натуральные числа делится число 509433?
Число 509433 делится на следующие целые, натуральные числа (все делители числа 509433): 1, 3, 47, 141, 3613, 10839, 169811, 509433
На какие четные числа делится число 509433?
Таких чисел нет.
На какие нечетные числа делится число 509433?
Число 509433 делится на следующие нечетные числа (нечетные делители числа): 1, 3, 47, 141, 3613, 10839, 169811, 509433
Сколько делителей имеет число 509433?
Число 509433 имеет 8 делителей
Сколько четных делителей имеет число 509433?
Число 509433 имеет 0 четных делителей
Сколько нечетных делителей имеет число 509433?
Число 509433 имеет 8 нечетных делителей
Число 509433 прописью, словами.
— пятьсот девять тысяч четыреста тридцать три
(что бы не забыть запишите число 509433 прописью в блокнот.)
Числа кратные 509433.
— кратные числа, числу 509433 : 1018866, 1528299, 2037732, 2547165, 3056598, 3566031, 4075464, 4584897, 5094330, 5603763, 6113196 и многие другие.
Простые множители числа 509433.
Простые множители числа 509433 = 3, 47, 3613 (единица также является простым множителем числа 509433)
Сумма цифр числа 509433.
Сумма цифр числа 509433 равна 24
Произведение цифр числа 509433.
Произведение цифр числа 509433 равна 0
Квадрат числа 509433.
Квадрат числа 509433 равен 259521981489
Куб числа 509433.
Куб числа 509433 равен 132209061595885737
Квадратный корень числа 509433.
Квадратный корень числа 509433 равен 713.7457.
Число 509433 в двоичной системе счисления.
Запись числа 509433 в двоичной системе счисления выглядит так: 1111100010111111001
Количество значащих нулей в двоичной записи числа 509433 = 6
Количество едениц в двоичной записи числа 509433 = 13
(что бы не забыть запишите число 509433 в двоичной системе счисления в блокнот.)Число 509433 в шестнадцатеричной системе счисления.
Запись числа 509433 в шестнадцатеричной системе счисления выглядит так: 7c5f9
(что бы не забыть запишите число 509433 в шестнадцатеричной системе счисления в блокнот.)Число 509433 в восьмеричной системе счисления.
Запись числа 509433 в восьмеричной системе счисления выглядит так: 1742771
(что бы не забыть запишите число 509433 в восьмеричной системе счисления в блокнот.)Число 509433 не является простым!
Корни числа 509433.
Корень 3 степени из 509433.
Корень 3 (третьей) степени из 509433 равен 79.866078019722
Корень 4 степени из 509433.
Корень 4 (четвертой) степени из 509433 равен 26.716020531736
Корень 5 степени из 509433.
Корень 5 (пятой) степени из 509433 равен 13.848968098098
Корень 6 степени из 509433.
Корень 6 (шестой) степени из 509433 равен 8.9367823079519
Корень 7 степени из 509433.
Корень 7 (седьмой) степени из 509433 равен 6.5357909621018
Корень 8 степени из 509433.
Корень 8 (восьмой) степени из 509433 равен 5.1687542533706
Корень 9 степени из 509433.
Корень 9 (девятой) степени из 509433 равен 4.3064636524809
Корень 10 степени из 509433.
Корень 10 (десятой) степени из 509433 равен 3.7214201722055
Корень 11 степени из 509433.
Корень 11 (одиннадцатой) степени из 509433 равен 3.3023727931426
Корень 12 степени из 509433.
Корень 12 (двенадцатой) степени из 509433 равен 2.9894451505174
Корень 13 степени из 509433.
Корень 13 (тринадцатой) степени из 509433 равен 2.7479365335262
Корень 14 степени из 509433.
Корень 14 (четырнадцатой) степени из 509433 равен 2.5565193060295
Корень 15 степени из 509433.
Корень 15 (пятнадцатой) степени из 509433 равен 2.4014440440504
Степени числа 509433.
509433 в 3 степени.
509433 в 3 степени равно 132209061595885737.
509433 в 4 степени.
509433 в 4 степени равно 6.7351658875977E+22.
509433 в 5 степени.
509433 в 5 степени равно 3.4311157636166E+28.
509433 в 6 степени.
509433 в 6 степени равно 1.7479235968065E+34.
509433 в 7 степени.
509433 в 7 степени равно 8.9044996169191E+39.
509433 в 8 степени.
509433 в 8 степени равно 4.536245953346E+45.
509433 в 9 степени.
509433 в 9 степени равно 2.3109133847509E+51.
509433 в 10 степени.
509433 в 10 степени равно 1.1772555383338E+57.
509433 в 11 степени.
509433 в 11 степени равно 5.9973282066E+62.
509433 в 12 степени.
509433 в 12 степени равно 3.0552369002729E+68.
509433 в 13 степени.
509433 в 13 степени равно 1.5564384998167E+74.
509433 в 14 степени.
509433 в 14 степени равно 7.9290113427713E+79.
509433 в 15 степени.
509433 в 15 степени равно 4.039300035382E+85.
Какое число имеет такую же сумму цифр как и число 509433?Математика. Найти сумму цифр числа 509433.
Число 509433 состоит из следующих цифр — 5, 0, 9, 4, 3, 3.
Определить сумму цифр числа 509433 не так уж и сложно.
Сумма цифр шестизначного числа 509433 равна 5 + 0 + 9 + 4 + 3 + 3 = 24.
Числа сумма цифр которых равна 24.
Следующие числа имеют такую же сумму цифр как и число 509433 — 699, 789, 798, 879, 888, 897, 969, 978, 987, 996, 1599, 1689, 1698, 1779, 1788, 1797, 1869, 1878, 1887, 1896.
Трехзначные числа сумма цифр которых равна 24 — 699, 789, 798, 879, 888, 897, 969, 978, 987, 996.
Четырехзначные числа сумма цифр которых равна 24 — 1599, 1689, 1698, 1779, 1788, 1797, 1869, 1878, 1887, 1896.
Пятизначные числа сумма цифр которых равна 24 — 10599, 10689, 10698, 10779, 10788, 10797, 10869, 10878, 10887, 10896.
Шестизначные числа сумма цифр которых равна 24 — 100599, 100689, 100698, 100779, 100788, 100797, 100869, 100878, 100887, 100896.
Квадрат суммы цифр числа 509433.
Квадрат суммы цифр шестизначного числа 509433 равен 5 + 0 + 9 + 4 + 3 + 3 = 24² = 576.
Сумма квадратов цифр шестизначного числа 509433.
Сумма квадратов цифр числа 509433 равна 5² + 0² + 9² + 4² + 3² + 3² = 25 + 0 + 81 + 16 + 9 + 9 = 140.
Сумма четных цифр числа 509433.
Сумма четных цифр шестизначного числа 509433 равна 4 = 4.
Квадрат суммы четных цифр шестизначного числа 509433.
Квадрат суммы четных цифр числа 509433 равна 4 = 4² = 16.
Сумма квадратов четных цифр шестизначного числа 509433.
Сумма квадратов четных цифр числа 509433 равна 4² = 16 = 16.
Сумма нечетных цифр числа 509433.
Сумма нечетных цифр шестизначного числа 509433 равна 5 + 9 + 3 + 3 = 20.
Квадрат суммы нечетных цифр шестизначного числа 509433.
Квадрат суммы нечетных цифр числа 509433 равна 5 + 9 + 3 + 3 = 20² = 400.
Сумма квадратов нечетных цифр шестизначного числа 509433.
Сумма квадратов нечетных цифр числа 509433 равна 5² + 9² + 3² + 3² = 25 + 81 + 9 + 9 = 124.
Произведение цифр числа 509433.
Какое число имеет такое же произведение цифр как и число 509433?Математика. Найти произведение цифр числа 509433.
Число 509433 состоит из следующих цифр — 5, 0, 9, 4, 3, 3.
Найти сумму цифр числа 509433 просто.
Решение:
Произведение цифр числа 509433 равно 5 * 0 * 9 * 4 * 3 * 3 = 0.
Числа произведение цифр которых равно 0.
Следующие числа имеют такое же произведение цифр как и число 509433 — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.
Двухзначные числа произведение цифр которых равно 0 — 10, 20, 30, 40, 50, 60, 70, 80, 90.
Трехзначные числа произведение цифр которых равно 0 — 100, 101, 102, 103, 104, 105, 106, 107, 108, 109.
Четырехзначные числа произведение цифр которых равно 0 — 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009.
Пятизначные числа произведение цифр которых равно 0 — 10000, 10001, 10002, 10003, 10004, 10005, 10006, 10007, 10008, 10009.
Шестизначные числа произведение цифр которых равно 0 — 100000, 100001, 100002, 100003, 100004, 100005, 100006, 100007, 100008, 100009.
Квадрат произведения цифр числа 509433.
Квадрат произведения цифр шестизначного числа 509433 равен 5 * 0 * 9 * 4 * 3 * 3 = 0² = 0.
Произведение квадратов цифр шестизначного числа 509433.
Произведение квадратов цифр числа 509433 равна 5² * 0² * 9² * 4² * 3² * 3² = 25 * 0 * 81 * 16 * 9 * 9 = 0.
Произведение четных цифр числа 509433.
Произведение четных цифр шестизначного числа 509433 равно 4 = 4.
Квадрат произведения четных цифр шестизначного числа 509433.
Квадрат произведения четных цифр числа 509433 равен 4 = 4² = 16.
Произведение квадратов четных цифр шестизначного числа 509433.
Произведение квадратов четных цифр числа 509433 равно 4² = 16 = 16.
Запишите числа которые в сумме дают число 509433.
Задача: Данно число 509433.Какие 2(два) числа дают в сумме число 509433?Решение:
1) 146441 + 362992 = 509433
2) 161423 + 348010 = 509433
3) 115237 + 394196 = 509433
4) 25237 + 484196 = 509433
5) 29253 + 480180 = 509433
Какие 3(три) числа дают в сумме число 509433?Решение:
1) 32948 + 61998 + 414487 = 509433
2) 16597 + 106485 + 386351 = 509433
3) 157858 + 28152 + 323423 = 509433
4) 124787 + 19274 + 365372 = 509433
5) 62028 + 37673 + 409732 = 509433
Какие 4(четыре) числа дают в сумме число 509433?Решение:
1) 53721 + 141233 + 60899 + 253580 = 509433
2) 101515 + 54619 + 51310 + 301989 = 509433
3) 67529 + 93516 + 164119 + 184269 = 509433
4) 24555 + 910 + 27778 + 456190 = 509433
5) 114213 + 21232 + 131765 + 242223 = 509433
Какие 5(пять) чисел дают в сумме число 509433?Решение:
1) 28733 + 57190 + 114456 + 118179 + 190875 = 509433
2) 13746 + 8234 + 42384 + 220154 + 224915 = 509433
3) 73319 + 97727 + 112499 + 32717 + 193171 = 509433
4) 54996 + 46273 + 76111 + 79518 + 252535 = 509433
5) 42764 + 58210 + 139707 + 22068 + 246684 = 509433
Задание 1
Основания равнобедренной трапеции равны 45 и 24. Тангенс острого угла равен $$frac{2}{7}$$. Найдите высоту трапеции.
Ответ: 9
Скрыть
Задание 2
Куб описан около сферы радиуса 12,5. Найдите объём куба.
Ответ: 15625
Скрыть
Задание 3
Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Ответ: 0,01
Скрыть
Задание 4
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 9 очков в двух играх. Если команда выигрывает, она получает 7 очков, в случае ничьей — 2 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
Ответ: 0,28
Скрыть
Задание 5
Найдите корень уравнения $$sqrt{frac{160}{6-7x}}=1frac{1}{3}$$
Ответ: -12
Скрыть
Задание 6
Найдите значение выражения $$2^{4log_{4}12}$$.
Ответ: 144
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-7; 7)$$. Найдите сумму точек экстремума функции $$f(x)$$.
Ответ: -1
Скрыть
Задание 8
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 744 МГц. Скорость погружения батискафа $$v$$ вычисляется по формуле $$v=ccdot frac{f-f_{0}}{ f+f_{0}}$$ где $$c=1500$$ м/с — скорость звука в воде, $$f_{0}$$ — частота испускаемых импульсов, $$f$$ — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Ответ: 756
Скрыть
Задание 9
Первый насос наполняет бак за 35 минут, второй — за 1 час 24 минуты, а третий — за 1 час 45 минут. За сколько минут наполнят бак три насоса, работая одновременно?
Ответ: 20
Скрыть
Задание 10
На рисунке изображён график функции $$f(x)=log_{a}(x-2)$$. Найдите $$f(10)$$.
Ответ: -3
Скрыть
Задание 11
Найдите точку максимума функции $$y=(4x^{2}-36x+36)e^{33-x}$$.
Ответ: 9
Скрыть
Задание 12
а) Решите уравнение $$2cos xcdot sin 2x=2sin x+cos 2x$$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[3pi;frac{9pi}{2}]$$.
Ответ: а)$$frac{pi}{4}+frac{pi n}{2};$$$$frac{pi}{6}+2pi m;$$$$frac{5pi}{6}+2pi k$$,n,m,kin Z$$ б)$$frac{13pi}{4};frac{15pi}{4};frac{25pi}{6};frac{17pi}{4}$$
Скрыть
Задание 13
Грань $$ABCD$$ куба $$ABCDA_{1}B_{1}C_{l}D_{1}$$ является вписанной в основание конуса, а сечением конуса плоскостью $$A_{1}B_{1}C_{1}$$ является круг, вписанный в четырёхугольник $$A_{1}B_{1}C_{l}D_{1}$$.
а) Высота конуса равна $$h$$, ребро куба равно $$a$$. Докажите, что $$3a<h<3,5a$$.
б) Найдите угол между плоскостями $$ABC$$ и $$SA_{1}D$$, где $$S$$ — вершина конуса.
Ответ: $$arctg (sqrt{6}+2sqrt{3})$$
Скрыть
Задание 14
Решите неравенство $$4log_{0,25}(1-4x)-log_{sqrt{2}}(-1-x)+4log_{4}(x^{2}-1)leq log_{2}x^{2}$$.
Ответ: $$(-infty;-1)$$
Скрыть
Задание 15
В июле Егор планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Егору оформить кредит на следующих условиях:
— в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая — может быть разным для разных годов);
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 15, 20 и 10 процентов соответственно, а во втором — 20, 10 и 15 процентов. Егор выбрал наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 13 до 14 тысяч рублей.
Ответ: 7 млн. руб.
Скрыть
Задание 16
На сторонах $$AB$$ и $$CD$$ четырёхугольника $$ABCD$$, около которого можно описать окружность, отмечены точки $$K$$ и $$N$$ соответственно. Около четырёхугольников $$AKND$$ и $$BCNK$$ также можно описать окружность. Косинус одного из углов четырёхугольника $$ABCD$$ равен 0,25.
а) Докажите, что четырёхугольник $$ABCD$$ является равнобедренной трапецией.
б) Найдите радиус окружности, описанной около четырёхугольника $$AKND$$, если радиус окружности, описанной около четырёхугольника $$ABCD$$, равен 8, $$AK:KB=2:5$$, a $$BC<AD$$ и $$ВС=4$$.
Ответ: $$frac{2sqrt{69}}{3}$$
Скрыть
Задание 17
Найдите все такие значения $$a$$, при каждом из которых уравнение $$sqrt{10x^{2}+x-24}cdotlog_{2}((x-3)cdot(a+5)+14)=0$$ имеет ровно два различных корня.
Ответ: $$-5;[-frac{50}{23};-frac{45}{23});(frac{11}{3};frac{13}{3})$$
Скрыть
Задание 18
Есть три коробки: в первой — 97 камней; во второй — 80, а в третьей коробке камней нет. Берут по одному камню из двух коробок и кладут их в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 58 камней, во второй — 59, а в третьей — 60?
б) Может ли в первой и второй коробках камней оказаться поровну?
в) Какое наибольшее количество камней может оказаться во второй коробке?
Ответ: а)да б)нет в)176
Скрыть
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Джинни и Джорджия 1-2 сезон смотреть онлайн
После смерти своего мужа 30 летняя женщина Джорджия Миллер решает начать жизнь с чистого листа. Поэтому она решает переехать в Новую Англию вместе со своими детьми, дочерью Джинни и сыном Остином. Устав от многочисленных переездов, дети искренне желают наконец-то осесть на одном месте и жить, не оглядываясь на прошлое своей матери. Джорджия из-за своих прошлых ошибок вынуждена постоянно менять место жительство. Разный взгляд на будущее приводит к разногласиям и конфликтам между женщиной и её детьми. Несмотря на все неурядицы, Новая Англия понравилась Джинни некоторыми перспективами, поскольку именно здесь юной девушке представилась возможность учиться в элитной школе и общаться с интересными людьми.
Поскольку Джорджия совершила большое количество ошибок в прошлом, она всячески стремится оградить детей от необдуманных поступков и решений. Несмотря на это, женщина до сих пор считает себя молодой девушкой. Поэтому она желает найти того единственного мужчину, с которым она смогла бы прожить всю свою жизнь. Такое легкомысленное поведение матери пугает Джинни, ведь Джорджия всё больше времени, сил и внимания уделяет новым ухажёрам. К каким последствиям приведёт такое поведение женщины?
- Оригинальное название: Ginny & Georgia
- Год выхода: 2021
- Страна: США
- Премьера: 24 февраля 2021
- Режиссер: Аня Адамс, Каталина Агиляр Мастретта, Renuka Jeyapalan
- Перевод: TVShows
- Качество: FHD (1080p)
- Статус сериала: На паузе
-
7.5
7.4
- Актеры: Брианна Хоуи, Антония Джентри, Дизель Ла Торрака, Дженнифер Робертсон, Феликс Маллард, Сара Вайсгласс, Скотт Портер, Реймонд Эблэк, Mason Temple, Кэти Дуглас
- Канал: Netflix
- Жанр: Драма, Комедия
«Джинни и Джорджия» смотреть онлайн бесплатно в хорошем качестве
Смотреть онлайн
Плеер 2
Трейлер
Свет
Добавить в закладки
Подписывайтесь на нашу группу в VK
Решение и ответы заданий Варианта №14 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
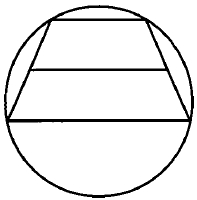
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 28. Найдите радиус описанной окружности этой трапеции.
Задание 2.
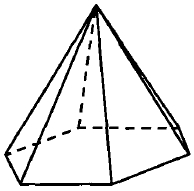
Сторона основания правильной шестиугольной пирамиды равна 3, боковое ребро равно 6. Найдите объём пирамиды.
Задание 3.
Из множества натуральных чисел от 56 до 80 (включительно) наудачу выбирают одно число. Какова вероятность того, что оно делится на 4?
Задание 4.
В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,2. Вероятность того, что чай закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
Задание 5.
Решите уравнение frac{7x}{3x^{2}–26}=1. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Задание 6.
Найдите значение выражения 5√3–4·51+3√3:54√3–1.
Задание 7.
Материальная точка движется прямолинейно по закону
x(t) = –frac{1}{2}t4 + 4t3 – t2 – t + 14,
где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 5 с.
Задание 8.
Для обогрева помещения, температура в котором поддерживается на уровне Тп = 15 °C, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,5 кг/с. Проходя по трубе расстояние х, вода охлаждается от начальной температуры Тв = 79 °C до температуры Т, причём
где с = 4200 Вт·с/кг·°C – теплоёмкость воды, γ = 63 Вт/м·°C – коэффициент теплообмена, а α = 1,3 – постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 130 м.
Задание 9.
Имеется два сплава. Первый сплав содержит 5 % никеля, второй – 14 % никеля. Масса второго сплава больше массы первого на 8 кг. Из этих двух сплавов получили третий сплав, содержащий 11 % никеля. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задание 10.
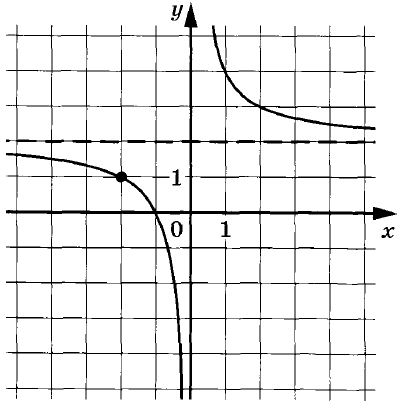
На рисунке изображён график функции f(х) = frac{k}{x} + а. Найдите, при каком значении х значение функции равно 7.
Задание 11.
Найдите наименьшее значение функции y = 49x – 46sinx + 37 на отрезке [-frac{pi}{2}; 0].
Задание 12.
а) Решите уравнение 25x–0,5 – 13·10x–1 + 4x+0,5 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{pi}{2}; π].
Задание 13.
В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1. Точка К – середина ребра A1C1.
а) Докажите, что плоскость MNK проходит через вершину В1.
б) Найдите расстояние от точки С до плоскости KMN, если АВ = 6, АА1 = 2,4.
Задание 14.
Решите неравенство 8lg(–1 – х) ≤ (х2 – 1)lg2.
Задание 15.
По вкладу «А» банк в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивает эту сумму на 14 % в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Задание 16.
В параллелограмме ABCD тангенс угла А равен 1,5. На продолжениях сторон АВ и ВС параллелограмма за точку В выбраны точки N и М соответственно, причём BC = CN и АВ = AM.
а) Докажите, что DN = DM.
б) Найдите MN, если АС = √13.
Задание 17.
Найдите все положительные значения а, при каждом из которых корни уравнения 5а2х – 2·4х + 9·(2а)x = 0 принадлежат отрезку [–3; 1].
Задание 18.
Известно, что а, b, с, d, е и f – это различные, расставленные в некотором, возможно ином, порядке числа 2, 3, 4, 6, 7 и 16.
а) Может ли выполняться равенство frac{a}{b}+frac{c}{d}+frac{e}{f}=11?
б) Может ли выполняться равенство frac{a}{b}+frac{c}{d}+frac{e}{f}=frac{1345}{336}?
в) Какое наибольшее значение может принимать сумма frac{a}{b}+frac{c}{d}+frac{e}{f}?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.