Найдите наименьшее значение функции на отрезке [11; 24].
Спрятать решение
Решение.
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
Ответ: −1.
Задания
Версия для печати и копирования в MS Word
Задания Д4 № 27888
Найдите величину угла
Ответ дайте в градусах.
Спрятать решение
Решение.
Центральный угол, опирающийся на хорду АС равен 90°, поэтому меньшая дуга окружности, отсекаемая этой хордой, также равна 90°, а большая — равна 270°. Опирающийся на нее вписанный угол ABC равен ее половине т. е. 135°.
Ответ: 135.
Аналоги к заданию № 27887: 27888 27889 26234 26235 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.1.4 Окружность и круг, 5.1.5 Вписанная и описанная окружность треугольника, 5.5.1 Величина угла, градусная мера угла
Спрятать решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-13

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Тема 25.
Программирование — Обработка целочисленной информации
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
программирование — обработка целочисленной информации
25.01Маска числа
25.02Поиск делителей
25.03Числа-палиндромы
25.04Простые числа
25.05Прочие прототипы
Решаем задачу:
Пусть M — сумма минимального и максимального натурального делителей целого числа, не считая единицы и самого числа.
Если таких делителей нет, то считаем значение M равным нулю.
Напишите программу, которая перебирает целые числа, большие 452 021, в порядке возрастания и ищет среди них
такие, для которых значение М при делении на 7 дает в остатке 3. Вывести первые 5 найденных чисел и соответствующие
им значения М.
Показать ответ и решение
def m(n):
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return i + n // i
return 0
k = 0
for i in range(452021 + 1, 10000000000000):
if m(i) % 7 == 3:
print(i, m(i))
k += 1
if k == 5: break
Ответ:
452025 150678 452029 23810 452034 226019 452048 226026 452062 226033
Дата: 2016-01-26
21416
Категория: Вписанный угол
Метка: ЕГЭ-№1ОкружностьУглы
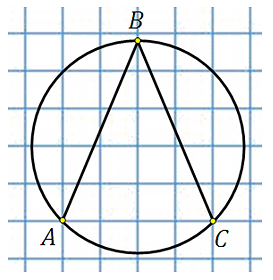
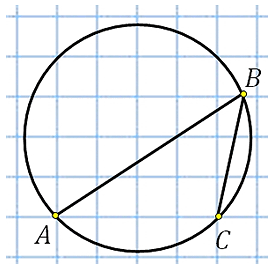
27887. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 900. Это видно по тому как проходят АО и ОС относительно клетчатой сетки. Угол АВС это вписанный угол, построенный на той же дуге.
По свойству вписанного угла:
Ответ: 45
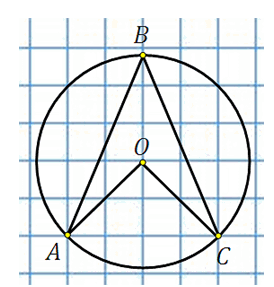
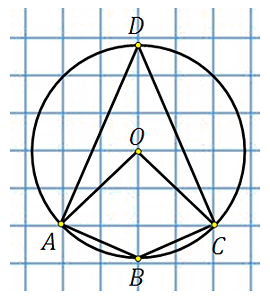
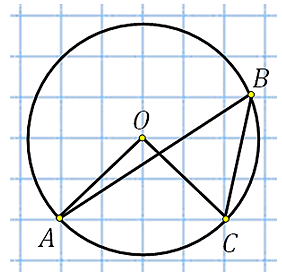
27888. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС и вписанный угол ADC:
Центральный угол АОС равен 900. По свойству вписанного угла
Известно, что у четырёхугольника вписанного в окружность сумма противоположных углов равна 180 градусам, следовательно:
Ответ: 135
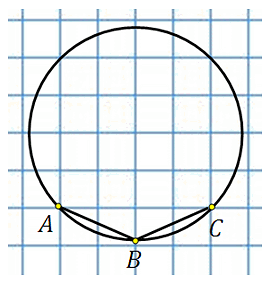
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности (видно о клетчатой сетке). Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 90 градусов. Угол АВС это вписанный угол, построенный на той же дуге. По свойству вписанного угла:
Ответ: 45
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
WEB-DL
- Год выхода: 2019
- Страна: Россия
- Жанр: Комедия
- Режиссер: Константин Смирнов, Константин Колесов
- Актёры: Вячеслав Чепурченко, Павел Комаров, Вадим Дубровин, Максим Лагашкин, Екатерина Стулова
- Сезоны: 1-3 сезон
- Серии: 1-16 серия
- Время: 00:30
Никита, Дэн и Артемий разработали уникальное приложение для смартфонов, вот-вот продадут его и осуществят все свои мечты. Но в последний момент многомиллионная сделка срывается и парней забирают в армию. Чтобы не ставить под угрозу успех своего стартапа, они выбирают альтернативную службу в глухой деревне Жуки, где будут пытаться довести свой проект до конца. Только не так просто разрабатывать приложение там, где нет даже интернета…
Смотреть онлайн Жуки (2019) в хорошем качестве HD
Плеер 1
Плеер 2
В закладки
Решение 18 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Угол между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C треугольника ABC, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шашистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шашистом из России.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Найдите корень уравнения (log_4{2^{5x+7}}=3).
Найдите значение выражения (dfrac{a^{3{,}33}}{a^{2{,}11}cdot a^{2{,}22}}) при (a=dfrac{2}{7}).
Прямая (y=9x+6) является касательной к графику (y=ax^2-19x+13). Найдите (a).
Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400) км − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Первый садовый насос перекачивает 10 литров воды за 5 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литров воды?
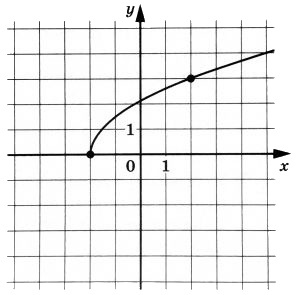
На рисунке изображен график функции (f(x)=ksqrt{x+p}). Найдите (f(0{,}25)).
Найдите наибольшее значение функции (y=2x^2-12x+8ln{x}-5) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right]).
а) Решите уравнение (7cos{x}-4cos^3{x}=2sqrt{3}sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-4pi;-3piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π |
Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=2AC.
Решите неравенство (log^2_{5}{left(x^4right)}-28log_{0{,}04}{left(x^2right)}leqslant 8).
Производство (x) тыс. единиц продуктции обходится в (q=3x^2+6x+13) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении (x)?
Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB=AC=17 и BC=16. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-a+3right)^2+left(y+a-2right)^2=a+dfrac{7}{2}, x-y=a-1 end{cases})имеет единственное решение.
Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{5}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{8}right]+left[dfrac{n}{23}right]=n+2021)?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Перейти к содержанию
Подборка заданий для подготовки к ЕГЭ по биологии. Задания с рисунками.
На чтение 1 мин Просмотров 19 Опубликовано 12 марта, 2023
Подборка заданий для подготовки к ЕГЭ по биологии. Задания с рисунками. Решение и ответы на задачи на официальном сайте источника онлайн.
В КИМах по биологии достаточное количество заданий с рисунками. Работа с ними часто вызывает затруднения у выпускников. Надеюсь, подборка материала (с сайта «Решу ЕГЭ» и открытого банка заданий ФИПИ) поможет ученикам качественно поготовиться к итоговой аттестации.
Варианты ответов и решение задачи — МАТЕРИАЛЫ ТУТ: https://nsportal.ru/shkola/biologiya/library/2016/09/03/podborka-zadaniy-dlya-podgotovki-k-ege-po-biologii-zadaniya-s
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Неотрицательное рациональное
шестизначное
число 509925
.
30 — сумма цифр числа.
У числа 509925 24 делителя.
И сумма этих делителей: 909664.
Обратным числом является 0.0000019610727067706035.
Число 509925 представляется произведением: 3 * 5 * 5 * 13 * 523.
Число 509925 в других системах счисления:
двоичная система: 1111100011111100101, троичная: 221220111010, восьмеричная: 1743745, шестнадцатеричная: 7C7E5.
497 килобайтов 997 байтов представляет из себя число байт 509925.
Азбука Морзе для числа 509925: ….. —— —-. —-. ..— …..
Косинус числа: 0.8628, синус числа: 0.5056, тангенс числа: 0.5860.
Натуральный логарифм числа: 13.1420.
Десятичный логарифм числа равен 5.7075.
714.0903 — квадратный корень из числа 509925, 79.8918 — кубический.
Возведение числа в квадрат: 2.6002e+11.
Конвертация из числа секунд это 5 дней 21 час 38 минут 45 секунд .
Нумерологическое значение числа 509925 – цифра 3.
Свойства натурального числа 509925, 0x07C7E5, 0x7C7E5:
Рейтинг 0 из 10,
оценок: 0.
Системы счисления, перевод в систему счисления
Десятичное число 509925
-
- 509925 в шестнадцатеричной системе счисления
- 7C7E5
-
- 509925 в двоичной системе счисления
- 1111100011111100101
-
- 509925 в восьмеричной системе счисления
- 1743745
Шестнадцатеричное число 7C7E5
-
- 7C7E5 в десятичной системе
- 509925
-
- 7C7E5 в двоичной системе
- 1111100011111100101
-
- 7C7E5 в восьмеричной системе
- 1743745
Двоичное число 1111100011111100101
-
- 1111100011111100101 в десятичной системе
- 509925
-
- 1111100011111100101 в шестнадцатеричной системе
- 7C7E5
-
- 1111100011111100101 в восьмеричной системе
- 1743745
Восьмеричное число 1743745
-
- 1743745 в десятичной системе
- 509925
-
- 1743745 в шестнадцатеричной системе
- 7C7E5
-
- 1743745 в двоичной системе
- 1111100011111100101
Основные арифметические и алгебраические свойства
-
- Число 509925 на русском языке, number in Russian, число 509925 прописью:
- пятьсот девять тысяч девятьсот двадцать пять
-
- Четность
- Нечетное число 509925
-
- Разложение на множители, делители числа 509925
- 3, 5, 5, 13, 523, 1
-
- Простое или составное число
- Составное число 509925
-
- Числа делящиеся на целое число 509925
- 1019850, 1529775, 2039700, 2549625, 3059550, 3569475, 4079400, 4589325
-
- Число 509925 умноженное на число два
- 1019850
-
- 509925 деленное на число 2
- 254962.5
-
- Список 8-ми простых чисел перед числом
- 509921, 509911, 509909, 509879, 509867, 509863, 509843, 509837
-
- Сумма десятичных цифр
- 30
-
- Количество цифр
- 6
-
- Десятичный логарифм 509925
- 5.7075063045658
-
- Натуральный логарифм 509925
- 13.142018935063
-
- Это число Фибоначчи?
- Нет
-
- Число на 1 больше числа 509925,
следующее число - число 509926
- Число на 1 больше числа 509925,
-
- Число на 1 меньше числа 509925,
предыдущее число - 509924
- Число на 1 меньше числа 509925,
Степени числа, корни
-
- 509925 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 260023505625
- 509925 во второй степени (в квадрате)
-
- В третьей степени (в кубе, 509925 в степени 3, x³) равно
- 132592486105828125
-
- Корень квадратный из 509925
- 714.09033042046
-
- Корень кубический из числа 509925 =
- 79.891780756786
Тригонометрические функции, тригонометрия
-
- Синус, sin 509925 градусов, sin 509925°
- 0.2588190451
-
- Косинус, cos 509925 градусов, cos 509925°
- -0.9659258263
-
- Тангенс, tg 509925 градусов, tg 509925°
- -0.2679491924
-
- Синус, sin 509925 радиан
- 0.50555510647425
-
- Косинус, cos 509925 радиан
- 0.86279431750436
-
- Тангенс, tg 509925 радиан равно
- 0.58595089955688
-
- 509925 градусов, 509925° =
- 8899.8701882321 радиан
-
- 509925 радиан =
- 29216550.368209 градуса, 29216550.368209°
Контрольные суммы, хэши, криптография
-
- MD-5 хэш(509925)
- 8671a82bf673aab3bad5244148990517
-
- CRC-32, CRC32(509925)
- 1494120029
-
- SHA-256 hash, SHA256(509925)
- 956071a18e55918a5fd3a8145bfc39aa69213710b871a430ba776120f1252630
-
- SHA1, SHA-1(509925)
- 98beb45e244cad9329d4a2cbaca22614d16874af
-
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(509925)
- e20fda488b298ef92bec21c278bf75d9264d9bbc7cf62c67d299e5bf136dc71a
-
- Base64
- NTA5OTI1
Языки программирования
-
- C++, CPP, C значение 509925
- 0x07C7E5, 0x7C7E5
-
- Delphi, Pascal значение числа 509925
- $07C7E5
Дата и время
-
- Конвертация UNIX timestamp 509925 в дату и время
-
- UTC
- вторник, 6 января 1970 г., 21:38:45 GMT
- в Москве, Россия
- среда, 7 января 1970 г., 0:38:45 Московское стандартное время
- в Лондоне, Великобритания
- вторник, 6 января 1970 г., 22:38:45 GMT+01:00
- в Нью-Йорке, США
- вторник, 6 января 1970 г., 16:38:45 Восточно-американское стандартное время
Интернет
-
- Конвертация в IPv4 адрес Интернет
- 0.7.199.229
-
- 509925 в Википедии:
- 509925
Другие свойства числа
-
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/509925
-
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x7C7E5
-
- Номер телефона
- 50-99-25
Цвет по числу 509925, цветовая гамма
-
- html RGB цвет 509925, 16-ричное значение
- #07C7E5 — (7, 199, 229)
-
- HTML CSS код цвета #07C7E5
- .color-mn { color: #07C7E5; }
.color-bg { background-color: #07C7E5; }
Цвет для данного числа 509925
Здесь вы можете изменить составляющую цвета для данного числа 509925 или цвета 07C7E5:
Задание 1
Основания равнобедренной трапеции равны 45 и 24. Тангенс острого угла равен $$frac{2}{7}$$. Найдите высоту трапеции.
Ответ: 9
Скрыть
Задание 2
Куб описан около сферы радиуса 12,5. Найдите объём куба.
Ответ: 15625
Скрыть
Задание 3
Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Ответ: 0,01
Скрыть
Задание 4
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 9 очков в двух играх. Если команда выигрывает, она получает 7 очков, в случае ничьей — 2 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
Ответ: 0,28
Скрыть
Задание 5
Найдите корень уравнения $$sqrt{frac{160}{6-7x}}=1frac{1}{3}$$
Ответ: -12
Скрыть
Задание 6
Найдите значение выражения $$2^{4log_{4}12}$$.
Ответ: 144
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-7; 7)$$. Найдите сумму точек экстремума функции $$f(x)$$.
Ответ: -1
Скрыть
Задание 8
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 744 МГц. Скорость погружения батискафа $$v$$ вычисляется по формуле $$v=ccdot frac{f-f_{0}}{ f+f_{0}}$$ где $$c=1500$$ м/с — скорость звука в воде, $$f_{0}$$ — частота испускаемых импульсов, $$f$$ — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Ответ: 756
Скрыть
Задание 9
Первый насос наполняет бак за 35 минут, второй — за 1 час 24 минуты, а третий — за 1 час 45 минут. За сколько минут наполнят бак три насоса, работая одновременно?
Ответ: 20
Скрыть
Задание 10
На рисунке изображён график функции $$f(x)=log_{a}(x-2)$$. Найдите $$f(10)$$.
Ответ: -3
Скрыть
Задание 11
Найдите точку максимума функции $$y=(4x^{2}-36x+36)e^{33-x}$$.
Ответ: 9
Скрыть
Задание 12
а) Решите уравнение $$2cos xcdot sin 2x=2sin x+cos 2x$$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[3pi;frac{9pi}{2}]$$.
Ответ: а)$$frac{pi}{4}+frac{pi n}{2};$$$$frac{pi}{6}+2pi m;$$$$frac{5pi}{6}+2pi k$$,n,m,kin Z$$ б)$$frac{13pi}{4};frac{15pi}{4};frac{25pi}{6};frac{17pi}{4}$$
Скрыть
Задание 13
Грань $$ABCD$$ куба $$ABCDA_{1}B_{1}C_{l}D_{1}$$ является вписанной в основание конуса, а сечением конуса плоскостью $$A_{1}B_{1}C_{1}$$ является круг, вписанный в четырёхугольник $$A_{1}B_{1}C_{l}D_{1}$$.
а) Высота конуса равна $$h$$, ребро куба равно $$a$$. Докажите, что $$3a<h<3,5a$$.
б) Найдите угол между плоскостями $$ABC$$ и $$SA_{1}D$$, где $$S$$ — вершина конуса.
Ответ: $$arctg (sqrt{6}+2sqrt{3})$$
Скрыть
Задание 14
Решите неравенство $$4log_{0,25}(1-4x)-log_{sqrt{2}}(-1-x)+4log_{4}(x^{2}-1)leq log_{2}x^{2}$$.
Ответ: $$(-infty;-1)$$
Скрыть
Задание 15
В июле Егор планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Егору оформить кредит на следующих условиях:
— в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая — может быть разным для разных годов);
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 15, 20 и 10 процентов соответственно, а во втором — 20, 10 и 15 процентов. Егор выбрал наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 13 до 14 тысяч рублей.
Ответ: 7 млн. руб.
Скрыть
Задание 16
На сторонах $$AB$$ и $$CD$$ четырёхугольника $$ABCD$$, около которого можно описать окружность, отмечены точки $$K$$ и $$N$$ соответственно. Около четырёхугольников $$AKND$$ и $$BCNK$$ также можно описать окружность. Косинус одного из углов четырёхугольника $$ABCD$$ равен 0,25.
а) Докажите, что четырёхугольник $$ABCD$$ является равнобедренной трапецией.
б) Найдите радиус окружности, описанной около четырёхугольника $$AKND$$, если радиус окружности, описанной около четырёхугольника $$ABCD$$, равен 8, $$AK:KB=2:5$$, a $$BC<AD$$ и $$ВС=4$$.
Ответ: $$frac{2sqrt{69}}{3}$$
Скрыть
Задание 17
Найдите все такие значения $$a$$, при каждом из которых уравнение $$sqrt{10x^{2}+x-24}cdotlog_{2}((x-3)cdot(a+5)+14)=0$$ имеет ровно два различных корня.
Ответ: $$-5;[-frac{50}{23};-frac{45}{23});(frac{11}{3};frac{13}{3})$$
Скрыть
Задание 18
Есть три коробки: в первой — 97 камней; во второй — 80, а в третьей коробке камней нет. Берут по одному камню из двух коробок и кладут их в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 58 камней, во второй — 59, а в третьей — 60?
б) Может ли в первой и второй коробках камней оказаться поровну?
в) Какое наибольшее количество камней может оказаться во второй коробке?
Ответ: а)да б)нет в)176
Скрыть