Расстояние между городами А и В равно 790 км. Из города А в город В выехал первый автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 85 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 450 км от города А. Ответ дайте в км/ч.
Спрятать решение
Решение.
Пусть км/ч — скорость первого автомобиля. Автомобиль, выехавший из города B, преодолел расстояние (790 − 450) км = 340 км. Первый автомобиль находился в пути на 2 часа больше, чем второй. Таким образом,
Ответ: 75.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Целое вещественное
шестизначное
число 509995
– составное.
Это полупростое число.
Произведение всех цифр числа: 0.
Число имеет следующие делители: 1, 5, 101999, 509995.
И сумма этих делителей: 612000.
Обратное число для 509995 — это 0.0000019608035372895815.
Это число представляется произведением простых чисел: 5 * 101999.
Системы счисления:
двоичная система счисления: 1111100100000101011, троичная система счисления: 221220120201, восьмеричная система счисления: 1744053, шестнадцатеричная система счисления: 7C82B.
Число байт 509995 представляет из себя 498 килобайтов 43 байта .
Число азбукой Морзе: ….. —— —-. —-. —-. …..
Косинус числа 509995: 0.1552, синус числа 509995: 0.9879, тангенс числа 509995: 6.3661.
Натуральный логарифм: 13.1422.
Число имеет десятичный логарифм: 5.7076.
714.1393 — квадратный корень, 79.8954 — кубический.
Возведение числа в квадрат: 2.6009e+11.
Число секунд 509995 представляет из себя 5 дней 21 час 39 минут 55 секунд .
Нумерологическое значение числа 509995 – цифра 1.
Финансовый консультант Марти Бёрд вместе с женой Вэнди и остальными членами семьи вынужден тайно переехать из престижного предместья Чикаго в курортный городок Озарк штата Миссури. К неожиданному переезду главного героя вынудили крупные долги, и на новом месте он надеется поправить своё финансовое положение.
- Название: Ozark
- Год выхода: 2017-07-21
- Страна: США
- Режиссер: Джейсон Бейтман, Алик Сахаров, Аманда Марсалис
- Статус сериала: Завершен
- Перевод: Пифагор
- Качество: FHD (1080p) (60 мин)
- Возраст: Сериал для зрителей старше 16+ лет
-
7.9
8.4
- В главных ролях: Джейсон Бейтман, Лора Линни, София Хьюблиц, Скайлар Гертнер, Джулия Гарнер, Лиза Эмери, Чарли Тахэн, Кевин Л. Джонсон, Джордана Спиро, Джейсон Батлер Харнер
- Подборки: Netflix, Про мафию, банды
- Жанры: Криминал, Триллер, Зарубежный, Драма
4 сезон 14 серия
Озарк смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет
Задание 1
Основания равнобедренной трапеции равны 45 и 24. Тангенс острого угла равен $$frac{2}{7}$$. Найдите высоту трапеции.
Ответ: 9
Скрыть
Задание 2
Куб описан около сферы радиуса 12,5. Найдите объём куба.
Ответ: 15625
Скрыть
Задание 3
Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Ответ: 0,01
Скрыть
Задание 4
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 9 очков в двух играх. Если команда выигрывает, она получает 7 очков, в случае ничьей — 2 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
Ответ: 0,28
Скрыть
Задание 5
Найдите корень уравнения $$sqrt{frac{160}{6-7x}}=1frac{1}{3}$$
Ответ: -12
Скрыть
Задание 6
Найдите значение выражения $$2^{4log_{4}12}$$.
Ответ: 144
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-7; 7)$$. Найдите сумму точек экстремума функции $$f(x)$$.
Ответ: -1
Скрыть
Задание 8
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 744 МГц. Скорость погружения батискафа $$v$$ вычисляется по формуле $$v=ccdot frac{f-f_{0}}{ f+f_{0}}$$ где $$c=1500$$ м/с — скорость звука в воде, $$f_{0}$$ — частота испускаемых импульсов, $$f$$ — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Ответ: 756
Скрыть
Задание 9
Первый насос наполняет бак за 35 минут, второй — за 1 час 24 минуты, а третий — за 1 час 45 минут. За сколько минут наполнят бак три насоса, работая одновременно?
Ответ: 20
Скрыть
Задание 10
На рисунке изображён график функции $$f(x)=log_{a}(x-2)$$. Найдите $$f(10)$$.
Ответ: -3
Скрыть
Задание 11
Найдите точку максимума функции $$y=(4x^{2}-36x+36)e^{33-x}$$.
Ответ: 9
Скрыть
Задание 12
а) Решите уравнение $$2cos xcdot sin 2x=2sin x+cos 2x$$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[3pi;frac{9pi}{2}]$$.
Ответ: а)$$frac{pi}{4}+frac{pi n}{2};$$$$frac{pi}{6}+2pi m;$$$$frac{5pi}{6}+2pi k$$,n,m,kin Z$$ б)$$frac{13pi}{4};frac{15pi}{4};frac{25pi}{6};frac{17pi}{4}$$
Скрыть
Задание 13
Грань $$ABCD$$ куба $$ABCDA_{1}B_{1}C_{l}D_{1}$$ является вписанной в основание конуса, а сечением конуса плоскостью $$A_{1}B_{1}C_{1}$$ является круг, вписанный в четырёхугольник $$A_{1}B_{1}C_{l}D_{1}$$.
а) Высота конуса равна $$h$$, ребро куба равно $$a$$. Докажите, что $$3a<h<3,5a$$.
б) Найдите угол между плоскостями $$ABC$$ и $$SA_{1}D$$, где $$S$$ — вершина конуса.
Ответ: $$arctg (sqrt{6}+2sqrt{3})$$
Скрыть
Задание 14
Решите неравенство $$4log_{0,25}(1-4x)-log_{sqrt{2}}(-1-x)+4log_{4}(x^{2}-1)leq log_{2}x^{2}$$.
Ответ: $$(-infty;-1)$$
Скрыть
Задание 15
В июле Егор планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Егору оформить кредит на следующих условиях:
— в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая — может быть разным для разных годов);
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 15, 20 и 10 процентов соответственно, а во втором — 20, 10 и 15 процентов. Егор выбрал наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 13 до 14 тысяч рублей.
Ответ: 7 млн. руб.
Скрыть
Задание 16
На сторонах $$AB$$ и $$CD$$ четырёхугольника $$ABCD$$, около которого можно описать окружность, отмечены точки $$K$$ и $$N$$ соответственно. Около четырёхугольников $$AKND$$ и $$BCNK$$ также можно описать окружность. Косинус одного из углов четырёхугольника $$ABCD$$ равен 0,25.
а) Докажите, что четырёхугольник $$ABCD$$ является равнобедренной трапецией.
б) Найдите радиус окружности, описанной около четырёхугольника $$AKND$$, если радиус окружности, описанной около четырёхугольника $$ABCD$$, равен 8, $$AK:KB=2:5$$, a $$BC<AD$$ и $$ВС=4$$.
Ответ: $$frac{2sqrt{69}}{3}$$
Скрыть
Задание 17
Найдите все такие значения $$a$$, при каждом из которых уравнение $$sqrt{10x^{2}+x-24}cdotlog_{2}((x-3)cdot(a+5)+14)=0$$ имеет ровно два различных корня.
Ответ: $$-5;[-frac{50}{23};-frac{45}{23});(frac{11}{3};frac{13}{3})$$
Скрыть
Задание 18
Есть три коробки: в первой — 97 камней; во второй — 80, а в третьей коробке камней нет. Берут по одному камню из двух коробок и кладут их в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 58 камней, во второй — 59, а в третьей — 60?
б) Может ли в первой и второй коробках камней оказаться поровну?
в) Какое наибольшее количество камней может оказаться во второй коробке?
Ответ: а)да б)нет в)176
Скрыть
Решение 25 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106°, угол CAD равен 69°. Найдите угол ABD. Ответ дайте в градусах.
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что AB=9, BC=6, AA₁=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁.
В магазине в одной коробке лежат вперемешку ручки с чёрными, синими или красными чернилами одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется чёрной, равна 0,37, а того, что она окажется синей, равна 0,45. Найдите вероятность того, что ручка окажется красной.
Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько раз стрелок должен выстрелить по мишени, чтобы поразить её с вероятностью не менее 0,4?
Найдите корень уравнения (sqrt{5x}=2dfrac12 x). Если уравнение имеет более одного корня, в ответе запишите больший из них.
Найдите значение выражения (cos alpha), если (mathrm{tg,}alpha =-dfrac{sqrt{21}}{2}) и (alphainleft(dfrac{3pi}{2};2piright))
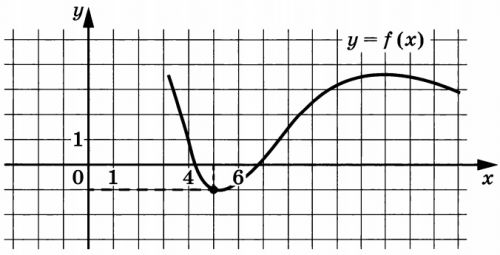
На рисунке изображён график функции (y=f(x)). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 5. Найдите значение производной функции в точке (x_0= 5).
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением (p_1V_1^{1{,}4}=p_2V_2^{1{,}4}), где (p_1) и (p_2) — давление газа (в атмосферах) в начальном и конечном состояниях, (V_1) и (V_2) — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 192 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Две трубы, работая одновременно, наполняют бассейн за 18 часов 40 минут, а одна первая труба наполняет бассейн за 40 часов. За сколько часов наполняет бассейн одна вторая труба?
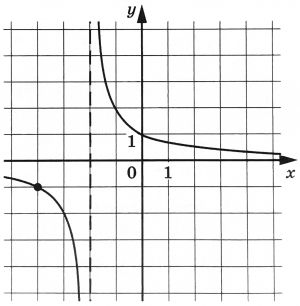
На рисунке изображён график функции (f(x)=dfrac{k}{x+a}). Найдите (f(-7)).
Найдите точку максимума функции (y=-dfrac{x^2+196}{x})
а) Решите уравнение (sin^4dfrac{x}4-cos^4dfrac{x}4=cosleft(x-dfrac{pi}2right))
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{3pi}2;piright])
В правильной шестиугольной призме (ABCDEFA_1B_1C_1D_1E_1F_1) сторона основания (AB) равна 4, а боковое ребро (AA_1) равно (5sqrt3). На ребре (DD_1) отмечена точка (M) так, что (DM:MD_1=3:2). Плоскость (alpha) параллельна прямой (A_1F_1) и проходит через точки (M) и (E).
а) Докажите, что сечение призмы (ABCDEFA_1B_1C_1D_1E_1F_1) плоскостью (alpha) – равнобедренная трапеция.
б) Найдите объем пирамиды, вершиной которой является точка (F), а основанием – сечение призмы (ABCDEFA_1B_1C_1D_1E_1F_1) плоскостью (alpha).
Решите неравенство (left(2cdot 0{,}5^{x+2}-0{,}5cdot 2^{x+2}right) left( 2log^2_{0{,}5}(x+2)-0{,}5log_2(x+2)right)leqslant 0)
15 января планируется взять кредит в банке на 2 года. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что за 15-й месяц кредитования нужно выплатить 44 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°.
а) Докажите, что углы BAP и POB равны.
б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6√3 и BP=4.
Найдите все значения (a), при каждом из которых среди корней уравнения (3x^2-24x+64=a|x-3|) будет ровно три положительных.
У Миши в копилке есть 2-рублевые, 5-рублевые и 10-рублевые монеты. Если взять 10 монет, то среди них обязательно найдется хотя бы одна 2-рублевая. Если взять 15 монет, то среди них обязательно найдется хотя бы одна 5-рублевая. Если взять 20 монет, то среди них найдется хотя бы одна 10-рублевая.
а) Может ли у Миши быть 30 монет?
б) Какое наибольшее количество монет может быть у Миши?
в) Какая наибольшая сумма рублей может быть у Миши?
Введите ответ в форме строки «да;123;1234». Где ответы на пункты разделены «;», и первый ответ с маленькой буквы.
ЕГЭ Профиль №1. Прямоугольный треугольник
Скачать файл в формате pdf.
ЕГЭ Профиль №1. Прямоугольный треугольник
| Задача 1. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (sin A = frac{7}{{25}}). Найдите АС.
Ответ
ОТВЕТ: 4,8. |
Задача 2. В треугольнике ABC угол C равен ({90^ circ }), (AB =  , (sin A = 0,5). Найдите ВС. , (sin A = 0,5). Найдите ВС.
Ответ
ОТВЕТ: 4. |
Задача 3. В треугольнике ABC угол C равен ({90^ circ }), (AB =  , (cos A = 0,5). Найдите AС. , (cos A = 0,5). Найдите AС.
Ответ
ОТВЕТ: 4. |
| Задача 4. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (cos A = frac{7}{{25}}). Найдите ВС.
Ответ
ОТВЕТ: 4,8. |
| Задача 5. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{33}}{{4sqrt {33} }}). Найдите AС.
Ответ
ОТВЕТ: 4. |
| Задача 6. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите BС.
Ответ
ОТВЕТ: 4. |
| Задача 7. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4,8), (sin A = frac{7}{{25}}). Найдите АB.
Ответ
ОТВЕТ: 5. |
| Задача 8. В треугольнике ABC угол C равен ({90^ circ }), (AC = 2), (sin A = frac{{sqrt {17} }}{{17}}). Найдите BC.
Ответ
ОТВЕТ: 0,5. |
| Задача 9. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (cos A = 0,5). Найдите АB.
Ответ
ОТВЕТ: 8. |
| Задача 10. В треугольнике ABC угол C равен ({90^ circ }), (AC = 0,5), (cos A = frac{{sqrt {17} }}{{17}}). Найдите BC.
Ответ
ОТВЕТ: 2. |
| Задача 11. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (tgA = frac{{33}}{{4sqrt {33} }}). Найдите АB.
Ответ
ОТВЕТ: 7. |
Задача 12. В треугольнике ABC угол C равен ({90^ circ }), (AC =  , ({text{tg}},A = 0,5). Найдите BC. , ({text{tg}},A = 0,5). Найдите BC.
Ответ
ОТВЕТ: 4. |
| Задача 13. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), (sin A = 0,5). Найдите АB.
Ответ
ОТВЕТ: 8. |
| Задача 14. В треугольнике ABC угол C равен ({90^ circ }), (BC = 0,5), (sin A = frac{{sqrt {17} }}{{17}}). Найдите AC.
Ответ
ОТВЕТ: 2. |
| Задача 15. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4,8), (cos A = frac{7}{{25}}). Найдите AB.
Ответ
ОТВЕТ: 5. |
| Задача 16. В треугольнике ABC угол C равен ({90^ circ }), (BC = 2), (cos A = frac{{sqrt {17} }}{{17}}). Найдите AC.
Ответ
ОТВЕТ: 0,5. |
| Задача 17. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите AB.
Ответ
ОТВЕТ: 7. |
| Задача 18. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = 0,5). Найдите AC.
Ответ
ОТВЕТ: 8. |
| Задача 19. В треугольнике ABC угол C равен ({90^ circ }), (AC = 24,;;BC = 7.) Найдите (sin A.)
Ответ
ОТВЕТ: 0,28. |
| Задача 20. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;;BC = 24.) Найдите (cos A.)
Ответ
ОТВЕТ: 0,28. |
| Задача 21. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;;BC = 4.) Найдите ({text{tg}},A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 22. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;BC = 4.) Найдите (sin A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 23. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;BC = 20.) Найдите (cos A.)
Ответ
ОТВЕТ: 0,6. |
| Задача 24. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;BC = 4.) Найдите ({text{tg}},A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 25. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;AC = 20.) Найдите (sinA.)
Ответ
ОТВЕТ: 0,6. |
| Задача 26. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;AC = 4.) Найдите (cos A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 27. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;AC = 8.) Найдите ({text{tg}},A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 28. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите AH.
Ответ
ОТВЕТ: 15. |
| Задача 29. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите BH.
Ответ
ОТВЕТ: 12. |
| Задача 30. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;sin A = 0,25.) Найдите высоту СH.
Ответ
ОТВЕТ: 3,75. |
| Задача 31. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите AH.
Ответ
ОТВЕТ: 12. |
| Задача 32. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите BH.
Ответ
ОТВЕТ: 15. |
| Задача 33. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;cos A = 0,25.) Найдите высоту СH.
Ответ
ОТВЕТ: 3,75. |
| Задача 34. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите AH.
Ответ
ОТВЕТ: 12,5. |
| Задача 35. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 13,;;{text{tg}},A = 5). Найдите BH.
Ответ
ОТВЕТ: 12,5. |
| Задача 36. В треугольнике ABC угол C равен ({90^ circ }), (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите высоту CH.
Ответ
ОТВЕТ: 2,5. |
| Задача 37. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 3,;;sin ,A = frac{1}{6}). Найдите AH.
Ответ
ОТВЕТ: 17,5. |
| Задача 38. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;sin ,A = 0,5.) Найдите BH.
Ответ
ОТВЕТ: 4. |
| Задача 39. В треугольнике ABC угол C равен ({90^ circ }), (BC = 5,;;sin ,A = frac{7}{{25}}.) Найдите высоту CH.
Ответ
ОТВЕТ: 4,8. |
| Задача 40. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 3,;;cos ,A = frac{{sqrt {35} }}{6}.) Найдите AH.
Ответ
ОТВЕТ: 17,5. |
| Задача 41. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 5,;;cos ,A = frac{7}{{25}}.) Найдите BH.
Ответ
ОТВЕТ: 4,8. |
| Задача 42. В треугольнике ABC угол C равен ({90^ circ }), (BC = 8,;;cos ,A = 0,5.) Найдите высоту CH.
Ответ
ОТВЕТ: 4. |
| Задача 43. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите BH.
Ответ
ОТВЕТ: 4. |
| Задача 44. В треугольнике ABC угол C равен ({90^ circ }), (BC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите высоту СH.
Ответ
ОТВЕТ: 4. |
| Задача 45. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;sin ,A = frac{{sqrt {35} }}{6}.) Найдите BH.
Ответ
ОТВЕТ: 17,5. |
| Задача 46. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;sin A = 0,5.) Найдите высоту СH.
Ответ
ОТВЕТ: 4. |
| Задача 47. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 8,;;cos ,A = 0,5.) Найдите AH.
Ответ
ОТВЕТ: 4. |
| Задача 48. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;cos ,A = frac{1}{6}.) Найдите BH.
Ответ
ОТВЕТ: 17,5. |
| Задача 49. В треугольнике ABC угол C равен ({90^ circ }), (AC = 5,;cos A = frac{7}{{25}}.) Найдите высоту СH.
Ответ
ОТВЕТ: 4,8. |
| Задача 50. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите AH.
Ответ
ОТВЕТ: 4. |
| Задача 51. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите высоту СH.
Ответ
ОТВЕТ: 4. |
| Задача 52. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;BH = 4.) Найдите (sin A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 53. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 25,;;BH = 20.) Найдите (cos A.)
Ответ
ОТВЕТ: 0,6. |
| Задача 54. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 4sqrt 5 ,;;BH = 4.) Найдите ({text{tg}},A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 55. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 20, (BC = 25.) Найдите (sin A.)
Ответ
ОТВЕТ: 0,6. |
| Задача 56. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = 8.) Найдите (cos A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 57. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = sqrt {17} .) Найдите ({text{tg}},A.)
Ответ
ОТВЕТ: 0,25. |
| Задача 58. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 24, (BH = 7.) Найдите (sin A.)
Ответ
ОТВЕТ: 0,28. |
| Задача 59. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 7, (BH = 24.) Найдите (cos A.)
Ответ
ОТВЕТ: 0,28. |
| Задача 60. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 8, (BH = 4.) Найдите ({text{tg}},A.)
Ответ
ОТВЕТ: 0,5. |
| Задача 61. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AH = 27,;;{text{tg}},A = frac{2}{3}.) Найдите BH.
Ответ
ОТВЕТ: 12. |
| Задача 62. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BH = 12,;;{text{tg}},A = frac{2}{3}.) Найдите AH.
Ответ
ОТВЕТ: 27. |
| Задача 63. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BH = 12,;;sin A = frac{2}{3}.) Найдите AB.
Ответ
ОТВЕТ: 27. |
| Задача 64. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AH = 12,;;cos A = frac{2}{3}.) Найдите AB.
Ответ
ОТВЕТ: 27. |
| Задача 65. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
Ответ
ОТВЕТ: 24. |
| Задача 66. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
Ответ
ОТВЕТ: 6. |
| Задача 67. В треугольнике ABC угол C равен ({90^ circ }), угол В равен ({58^ circ }), CD медиана. Найдите угол ACD. Ответ дайте в градусах.
Ответ
ОТВЕТ: 32. |
| Задача 68. Острый угол прямоугольного треугольника равен ({32^ circ }). Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Ответ
ОТВЕТ: 61. |
| Задача 69. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Ответ
ОТВЕТ: 45. |
| Задача 70. Один из углов прямоугольного треугольника равен ({29^ circ }). Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Ответ
ОТВЕТ: 16. |
| Задача 71. В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах. |
| Задача 72. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах. |
| Задача 73. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах. |
| Задача 74. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах. |
| Задача 75. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах. |
| Задача 76. В треугольнике ABC угол C равен 90°, угол A равен 30°, (AB = 2sqrt 3 ). Найдите высоту CH. |
| Задача 77. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, угол A равен 30°, (AB = 2). Найдите AH. |
| Задача 78. В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, (AB = 4). Найдите BH. |