31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Спрятать решение
Решение.
Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент m = 1 + 0,01k. После первой выплаты сумма долга составит: a1 = am − x. После второй выплаты сумма долга составит:
После третьей выплаты сумма оставшегося долга:
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому откуда
При a = 9 930 000 и k = 10, получаем: m = 1,1 и
Ответ: 3 993 000 рублей.
Приведём другое решение.
Пусть x — один из трёх разовых платежей. Тогда сумма долга после оплаты в первом году составит: После внесения второго платежа сумма долга станет равной
Сумма долга после третьего платежа:
Третьим платежом Сергей должен погасить долг, то есть долг станет равным нулю:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник: Демонстрационная версия ЕГЭ—2015 по математике. Профильный уровень.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1
Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.
Ответ: 1,5
Скрыть
Задание 2
Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.
Ответ: 12
Скрыть
Задание 3
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажира, равна 0,9. Вероятность того, что окажется меньше 9 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 9 до 17 включительно.
Ответ: 0,24
Скрыть
Задание 4
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Монтёр». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Ответ: 0,125
Скрыть
Задание 5
Решите уравнение $$cos frac{pi(8x+8)}{3}=frac{1}{2}$$. В ответе запишите наибольший отрицательный корень.
Ответ: 0,375
Скрыть
Задание 6
Найдите значение выражения $$frac{125^{3,2}}{25^{3,3}}$$
Ответ: 125
Скрыть
Задание 7
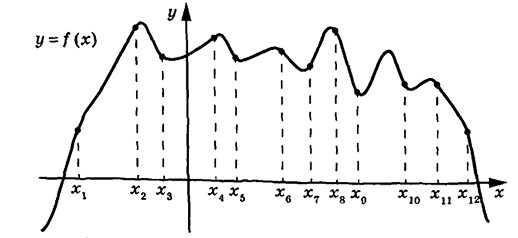
На рисунке изображён график функции $$y=f(x)$$. На оси абсцисс отмечено двенадцать точек: $$x_1$$, $$x_2$$, $$x_3$$, $$x_4$$, $$x_5$$, $$x_6$$, $$x_7$$, $$x_8$$, $$x_9$$, $$x_{10}$$, $$x_{11}$$, $$x_{12}$$. В ответе укажите количество точек (из отмеченных), в которых производная функции $$f(x)$$ отрицательна.
Ответ: 8
Скрыть
Задание 8
Наблюдатель находится на высоте $$h$$, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле $$l=sqrt{frac{Rh}{500}}$$, где $$R=6400$$ км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 60 километров? Ответ дайте в метрах.
Ответ: 281,25
Скрыть
Задание 9
Заказ на изготовление 216 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше?
Ответ: 18
Скрыть
Задание 10
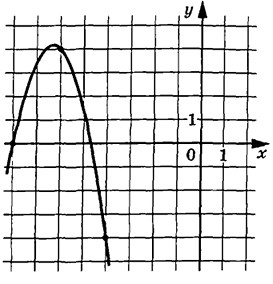
На рисунке изображён график функции $$f(x)=ax^2+bx+c$$. Найдите ординату точки пересечения графика функции $$y=f(x)$$ с осью ординат.
Ответ: -56
Скрыть
Задание 11
Найдите точку минимума функции $$y=10x-ln (x+11)+3$$.
Ответ: -10,9
Скрыть
Задание 12
а) Решите уравнение $$5^{x+sqrt{x}-1}+6cdot 5^{x-sqrt{x}+1}-5^{x+1}=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[1;2,56]$$
Ответ: а)$$log^{2}_{5}10;log^{2}_{5}15$$ б)$$log^{2}_{5}10$$
Скрыть
Задание 13
В прямой пятиугольной призме $$ABCDEA_1B_1C_1D_1E_1$$ высота равна $$2sqrt{3}$$ , треугольник $$BCD$$ — правильный, со стороной 6, а четырёхугольник $$ABDE$$ — равнобедренная трапеция со сторонами $$AB=DE=2$$, $$BD=6$$ и $$AE=4$$.
а) Докажите, что плоскости $$CA_1E_1$$ и $$AED_1$$ перпендикулярны.
б) Найдите объём многогранника $$CAED_1B_1$$.
Ответ: 40
Скрыть
Задание 14
Решите неравенство $$log_{tg 0,9}(log_{frac{1}{4}}(x^2-2))leq 0$$
Ответ: $$(-sqrt{3};-1,5];[1,5;sqrt{3})$$
Скрыть
Задание 15
В июле Борис планирует взять кредит в банке на некоторую сумму. Банк предложил Борису два варианта кредитования.
1-й вариант:
— кредит предоставляется на 3 года;
— в январе каждого года действия кредита долг увеличивается на 10 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью,
2-й вариант:
— кредит предоставляется на 2 года; — в январе каждого года действия кредита долг увеличивается на 16 %;
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Когда Борис подсчитал, то выяснил, что по 1-му варианту кредитования ему придётся выплачивать на 353 740 рублей меньше, чем по 2-му варианту. Какую сумму Борис планирует взять в кредит?
Ответ: 8937 тыс. руб.
Скрыть
Задание 16
Четырёхугольник $$ABCD$$ со сторонами $$BC=14$$ и $$AB=CD=40$$ вписан в окружность радиусом $$R=25$$.
а) Докажите, что прямые $$BC$$ и $$AD$$ параллельны.
б) Найдите $$AD$$.
Ответ: 42,16
Скрыть
Задание 17
Найдите все значения $$а$$, при каждом из которых уравнение $$frac{log_{0,2}(6x^2+13ax+7x+8a^2+2a-2)}{sqrt{4-3a-2x}}=0$$ имеет единственный корень.
Ответ: $$(-infty;-7];[2;+infty);-frac{11}{8}$$
Скрыть
Задание 18
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 8 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 4040.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из пяти членов?
в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а)да б)нет в)897
Скрыть
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 1 мин. 16 сек.
ЕГЭ по математике (база) 2023 задание 16: номер 441 | gzvne | Механические часы с двенадцат…
35
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки $11$, но не дойдя до отметки $2$ часа.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Найдите значение выражения ${6√{180}}/{√5}$.
Найдите значение выражения ${7^{-10}·7^5}/{7^{-7}}$.
Найдите значение выражения $(√{43} — 6)(√{43} + 6)$.
Найдите значение выражения ${(4^{-6})^2}/{4^{-14}}$.
Джинни и Джорджия 1-2 сезон смотреть онлайн
После смерти своего мужа 30 летняя женщина Джорджия Миллер решает начать жизнь с чистого листа. Поэтому она решает переехать в Новую Англию вместе со своими детьми, дочерью Джинни и сыном Остином. Устав от многочисленных переездов, дети искренне желают наконец-то осесть на одном месте и жить, не оглядываясь на прошлое своей матери. Джорджия из-за своих прошлых ошибок вынуждена постоянно менять место жительство. Разный взгляд на будущее приводит к разногласиям и конфликтам между женщиной и её детьми. Несмотря на все неурядицы, Новая Англия понравилась Джинни некоторыми перспективами, поскольку именно здесь юной девушке представилась возможность учиться в элитной школе и общаться с интересными людьми.
Поскольку Джорджия совершила большое количество ошибок в прошлом, она всячески стремится оградить детей от необдуманных поступков и решений. Несмотря на это, женщина до сих пор считает себя молодой девушкой. Поэтому она желает найти того единственного мужчину, с которым она смогла бы прожить всю свою жизнь. Такое легкомысленное поведение матери пугает Джинни, ведь Джорджия всё больше времени, сил и внимания уделяет новым ухажёрам. К каким последствиям приведёт такое поведение женщины?
- Оригинальное название: Ginny & Georgia
- Год выхода: 2021
- Страна: США
- Премьера: 24 февраля 2021
- Режиссер: Аня Адамс, Каталина Агиляр Мастретта, Renuka Jeyapalan
- Перевод: TVShows
- Качество: FHD (1080p)
- Статус сериала: На паузе
-
7.5
7.4
- Актеры: Брианна Хоуи, Антония Джентри, Дизель Ла Торрака, Дженнифер Робертсон, Феликс Маллард, Сара Вайсгласс, Скотт Портер, Реймонд Эблэк, Mason Temple, Кэти Дуглас
- Канал: Netflix
- Жанр: Драма, Комедия
«Джинни и Джорджия» смотреть онлайн бесплатно в хорошем качестве
Смотреть онлайн
Плеер 2
Трейлер
Свет
Добавить в закладки
Подписывайтесь на нашу группу в VK