СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 17 № 510182
Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Спрятать решение
Решение.
Преобразуем уравнение:
По теореме Виета для квадратного уравнения: Таким образом,
Наименьший корень
Ответ: 3.
Аналоги к заданию № 510182: 510281 511417 511437 511457 511477 511920 511940 514881 510161 510168 … Все
Раздел кодификатора ФИПИ: Линейные, квадратные, кубические уравнения
Номер в банке ФИПИ: 9D7FBA
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Решите систему уравнений:
Спрятать решение
Решение.
Система уравнений разбивается на совокупность двух систем:
Решим первое уравнение системы:
Аналогично из второй системы получаем пару решений
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Решите систему уравнений:
Спрятать решение
Решение.
Система уравнений разбивается на совокупность двух систем:
Решим первое уравнение системы:
Аналогично из второй системы получаем пару решений
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
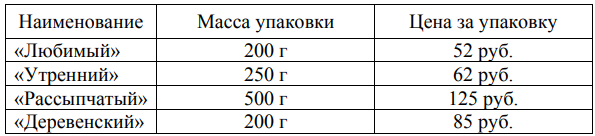
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
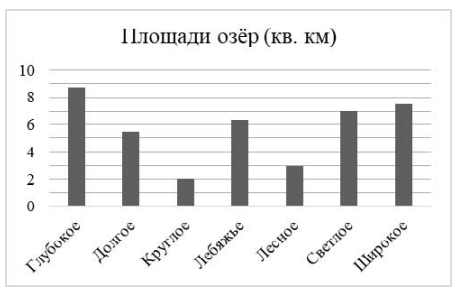
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
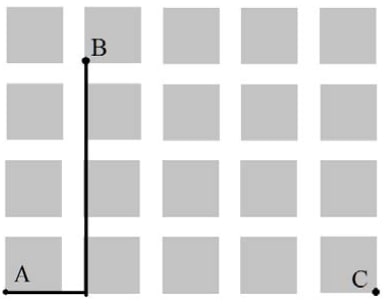
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 18 ЕГЭ 2022 математика 11 класс профильный уровень 30 задач с ответами, тема числовые наборы на карточках и числах, практические задачи для тренировки с ответами для подготовки к ЕГЭ 2022. Решаем!
Скачать задачи ЕГЭ 2022 с ответами
1)Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11. а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8, 10. б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22? в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Ответ: а) 2, 2, 2, 2, 2; б) нет; в) 7, 8, 8, 8, 10 или 7, 8, 10, 16.
2)На доске написано число 2015 и еще несколько (не менее двух) натуральных чисел, не превосходящих 5000. Все написанные на доске числа различны. Сумма любых двух из написанных чисел делится на какое-нибудь из остальных. а) Может ли на доске быть написано ровно 1009 чисел? б) Может ли на доске быть написано ровно пять чисел? в) Какое наименьшее количество чисел может быть написано на доске?
Ответ: а) Может. Например, числа 1,2,3,5,7,…,2015; б) Может. Например, числа 1, 2, 3, 5, 2015; в) 4, например, 1, 2, 3, 2015.
3)На доске было написано 20 натуральных чисел (не обязательно различных), каждое из которых не превосходит 40. Вместо некоторых из чисел (возможно, одного) на доске написали числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, с доски стѐрли. а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось? б) Среднее арифметическое первоначально написанных чисел равнялось 27. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 34? в) Среднее арифметическое первоначально написанных чисел равнялось 27. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Ответ: а) да; б) нет; в) 38 1/7
4)Задумано несколько целых чисел. Набор этих чисел и все их возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Например, если задуманы числа 2, 3, 5, то на доске будет выписан набор 2, 3, 5, 5, 7, 8, 10. а) На доске выписан набор −11, −7, −5, −4, −1, 2, 6. Какие числа были задуманы? б) Для некоторых различных задуманных чисел в наборе, выписанном на доске, число 0 встречается ровно 4 раза. Какое наименьшее количество чисел могло быть задумано? в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору можно однозначно определить задуманные числа?
Ответ: а) −7, −4, 6; б) 5; в) нет.
5)На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, среднее арифметическое всех отрицательных из них равно −8. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?
Ответ: а) 44; б) отрицательных; в) 17.
6)На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме какихто двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.). а) Может ли в какой-то момент на доске оказаться число 2012? б) Может ли в какой-то момент сумма всех чисел на доске равняться 63? в) Через какое наименьшее время на доске может появиться число 784?
Ответ: а) нет; б) да; в) 8 минут.
7)Каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9 по одному записывают на 8 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: а) нет; б) нет; в) 4.
8)Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Каково наименьшее возможное значение полученного результата?
Ответ: а) нет; б) нет; в) 4.
9)На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?
Ответ: а) 36; б) отрицательных; в) 16.
10)Из первых 22 натуральных чисел 1,2,…,22 выбрали 2 k различных чисел. Выбранные числа разбили на пары и посчитали суммы чисел в каждой паре. Оказалось, что все полученные суммы различны и не превосходят 27. а) Может ли получиться так, что сумма всех 2 k выбранных чисел равняется 170 и в каждой паре одно из чисел ровно в три раза больше другого? б) Может ли число k быть равным 11? в) Найдите наибольшее возможное значение числа k.
Ответ: а) нет; б) нет; в) 10.
11)На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлѐнная до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) например, числа 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01 и любая последовательность ходов; б) нет; в) 5.
12)На проекте «Мисс Чистополь − 2019» выступление каждой участницы оценивают шесть судей. При этом каждый судья выставляет оценку — целое число баллов от 0 до 10 включительно. Известно, что за выступление Ангелины Курбановой все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за выступление определяется как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки, и считается среднее арифметическое четырех оставшихся оценок. а) Могут ли итоговые баллы, вычисленные по старой и новой системам оценивания, оказаться одинаковыми? б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, оказаться равной 1 8 ? в) Найдите наибольшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания.
Ответ: а) да; б) нет; в) 5/6
13)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел. б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Ответ: а) 17 и 16; б) нет; в) 1650.
14)Набор состоит из 33 натуральных чисел, среди которых есть числа 3, 4 и 5. Среднее арифметическое любых 27 чисел этого набора меньше 2. а) Может ли такой набор содержать ровно 13 единиц? б) Может ли такой набор содержать менее 13 единиц? в) Докажите, что в любом таком наборе есть несколько чисел, сумма которых равна 28.
Ответ: а) да; б) нет.
15)Каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11. После этого числа на каждой карточке складывают, а полученные 10 сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: а) нет; б) нет; в) 4.
16)На доске написано несколько различных натуральных чисел, произведение любых двух из которых больше 40 и меньше 100. а) Может ли на доске быть 5 чисел? б) Может ли на доске быть 6 чисел? в) Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?
Ответ: а) да; б) нет; в) 35.
17)На доске написано несколько (более одного) различных натуральных чисел, причем любые два из них отличаются не более чем в три раза. а) Может ли на доске быть 5 чисел, сумма которых равна 47? б) Может ли на доске быть 10 чисел, сумма которых равна 94? в) Сколько может быть чисел на доске, если их произведение равно 8000?
Ответ: а) да; б) нет; в) 2 или 3.
18)Задумано несколько натуральных чисел (не обязательно различных). Эти числа и все их возможные произведения (по 2 числа, по 3 числа и т. д.) выписывают на доску. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляют одно такое число n, а остальные числа, равные n, стирают. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 9, 12, 36. а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90. б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 3, 5, 7, 9, 15, 21, 35, 45, 105, 315, 945? в) Приведите все примеры шести задуманных чисел, для которых на доске будет записан набор, наибольшее число в котором равно 82.
Ответ: а) 2, 3, 3, 5; б) нет; в) 1, 1, 1, 1, 1, 82 или 1, 1, 1, 1, 2, 41.
19)Задумано несколько натуральных чисел (не обязательно различных). Эти числа и все их возможные произведения (по 2 числа, по 3 числа и т. д.) выписывают на доску. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляют одно такое число n, а остальные числа, равные n, стирают. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 9, 12, 36. а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150. б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 2, 5, 10, 11, 22, 25, 55, 110, 275, 550? в) Приведите все примеры пяти задуманных чисел, для которых на доске будет записан набор, наибольшее число в котором равно 91.
Ответ: а) 2, 3, 5, 5; б) нет; в) 1, 1, 1, 1, 91 или 1, 1, 1, 7, 13.
20)Саша берѐт пять различных натуральных чисел и проделывает с ними следующие операции: сначала вычисляет среднее арифметическое первых двух чисел, затем среднее арифметическое результата и третьего числа, потом среднее арифметическое полученного результата и четвѐртого числа, потом среднее арифметическое полученного результата и пятого числа — число A. а) Может ли число A равняться среднему арифметическому начальных пяти чисел? б) Может ли число A быть больше среднего арифметического начальных чисел в пять раз? в) В какое наибольшее целое число раз число A может быть больше среднего арифметического начальных пяти чисел?
Ответ: а) да, например: 1, 3, 8, 11, 2; б) нет; в) 2.
21)На доске написано 30 натуральных чисел. Какие-то из них красные, а какие-то зелѐные. Красные числа кратны 7, а зелѐные числа кратны 5. Все красные числа отличаются друг от друга, как и все зелѐные. Но между красными и зелѐными могут быть одинаковые. а) Может ли сумма зелѐных чисел быть меньше 2325, если на доске написаны только кратные 5 числа? б) Может ли сумма чисел быть 1467, если только одно число красное? в) Найдите наименьшее количество красных чисел, которое может быть при сумме 1467.
Ответ: а) Да; б) нет; в) 10.
22)На доске написано 30 натуральных чисел. Какие-то из них красные, а какие-то зелѐные. Красные числа кратны 8, а зелѐные числа кратны 3. Все красные числа отличаются друг от друга, как и все зелѐные. Но между красными и зелѐными могут быть одинаковые. а) Может ли сумма зелѐных чисел быть меньше 1395 = 3 + 6 +…+ 90, если на доске написаны только кратные 3 числа? б) Может ли сумма чисел быть 1066, если только одно число красное? в) Найдите наименьшее количество красных чисел, которое может быть при сумме 1066.
Ответ: а) Да; б) нет; в) 7.
23)На доске написано 100 различных натуральных чисел с суммой 5100. а) Может ли быть записано число 250? б) Можно ли обойтись без числа 11? в) Какое наименьшее количество чисел, кратных 11, может быть на доске?
Ответ: а) Нет; б) нет; в) 6.
24)На доске написано 100 различных натуральных чисел с суммой 5120. а) Может ли быть записано число 230? б) Можно ли обойтись без числа 14? в) Какое наименьшее количество чисел, кратных 14, может быть на доске?
Ответ: а) Нет; б) нет; в) 4.
25)На доске написано 30 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись заканчивается на цифру 7. Сумма написанных чисел равна 810. а) Может ли быть 24 четных числа? б) Может ли быть на доске ровно два числа, оканчивающихся на 7? в) Какое наименьшее количество чисел с последней цифрой 7 может быть на доске?
Ответ: а) да; б) нет; в) 4.
26)На доске написано 30 различных натуральных чисел, каждое или оканчивается на 9, или четное, а сумма чисел равна 877. а) Может ли быть на доске 27 четных чисел? б) Может ли быть на доске ровно два числа, оканчивающихся на 9? в) Какое наименьшее количество чисел с последней цифрой 9 может быть на доске?
Ответ: а) да; б) нет; в) 3.
27)В течение n дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли n быть больше 6? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 2, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 5. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
Ответ: а) да, б) да, в) 34.
28)На доске написано n единиц, между некоторыми из которых поставили знаки + и посчитали сумму. Например, если изначально было написано n = 12 единиц, то могла получиться, например, такая сумма: 1 + 11 + 11 + 111 + 11 + 1 + 1 = 147. а) Могла ли сумма равняться 150, если n = 60? б) Могла ли сумма равняться 150, если n = 80? в) Чему могло равняться n, если полученная сумма чисел равна 150?
Ответ: а) да, б) нет, в) 150, 141, 132, 123, 114, 105, 96, 87, 78, 69, 60, 51, 42, 33, 24, 15.
29)На доске написано несколько различных натуральных чисел, которые делятся на 3 и оканчиваются на 4. а) Может ли сумма составлять 282? б) Может ли их сумма составлять 390? в) Какое наибольшее количество чисел могло быть на доске, если их сумма равна 2226?
Ответ: а) да, б) нет, в) 9.
30)На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 6, к каждому числу из второй группы приписали справа цифру 9, а числа третьей группы оставили без изменений. а) Могла ли сумма всех этих чисел увеличиться в 9 раз? б) Могла ли сумма всех этих чисел увеличиться в 19 раз? в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Ответ: а) да, б) нет, в) в 11,6 раза.
31)На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго. а) Может ли сумма этих чисел быть равна 420? б) Может ли сумма этих чисел быть равна 419? в) В тройке чисел первое число трѐхзначное, а третье равно 5. Сколько существует таких троек?
Ответ: а) да, б) нет, в) 85.
Смотрите также на нашем сайте:
Числа и их свойства 18 задание ЕГЭ 2022 профиль математика с ответами
Задание 15 ЕГЭ 2022 математика профиль задачи на вклады, кредиты, оптимизацию
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Джинни и Джорджия 1-2 сезон смотреть онлайн
После смерти своего мужа 30 летняя женщина Джорджия Миллер решает начать жизнь с чистого листа. Поэтому она решает переехать в Новую Англию вместе со своими детьми, дочерью Джинни и сыном Остином. Устав от многочисленных переездов, дети искренне желают наконец-то осесть на одном месте и жить, не оглядываясь на прошлое своей матери. Джорджия из-за своих прошлых ошибок вынуждена постоянно менять место жительство. Разный взгляд на будущее приводит к разногласиям и конфликтам между женщиной и её детьми. Несмотря на все неурядицы, Новая Англия понравилась Джинни некоторыми перспективами, поскольку именно здесь юной девушке представилась возможность учиться в элитной школе и общаться с интересными людьми.
Поскольку Джорджия совершила большое количество ошибок в прошлом, она всячески стремится оградить детей от необдуманных поступков и решений. Несмотря на это, женщина до сих пор считает себя молодой девушкой. Поэтому она желает найти того единственного мужчину, с которым она смогла бы прожить всю свою жизнь. Такое легкомысленное поведение матери пугает Джинни, ведь Джорджия всё больше времени, сил и внимания уделяет новым ухажёрам. К каким последствиям приведёт такое поведение женщины?
- Оригинальное название: Ginny & Georgia
- Год выхода: 2021
- Страна: США
- Премьера: 24 февраля 2021
- Режиссер: Аня Адамс, Каталина Агиляр Мастретта, Renuka Jeyapalan
- Перевод: TVShows
- Качество: FHD (1080p)
- Статус сериала: На паузе
-
7.5
7.4
- Актеры: Брианна Хоуи, Антония Джентри, Дизель Ла Торрака, Дженнифер Робертсон, Феликс Маллард, Сара Вайсгласс, Скотт Портер, Реймонд Эблэк, Mason Temple, Кэти Дуглас
- Канал: Netflix
- Жанр: Драма, Комедия
«Джинни и Джорджия» смотреть онлайн бесплатно в хорошем качестве
Смотреть онлайн
Плеер 2
Трейлер
Свет
Добавить в закладки
Подписывайтесь на нашу группу в VK
Егэ математика 510182
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 9 № 510182
Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите меньший из них.
По теореме Виета для квадратного уравнения: Таким образом, Наименьший корень
—>
Задание 9 № 510182
Егэ математика 510182.
Mathb-ege. sdamgia. ru
30.08.2017 19:02:27
2017-08-30 19:02:27
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=510182
Решу ЕГЭ математика профиль 2022 » /> » /> .keyword { color: red; } Егэ математика 510182
Решу ЕГЭ математика профиль 2022 — базовый и профильный уровни экзамена
Решу ЕГЭ математика профиль 2022 — базовый и профильный уровни экзамена
Решу ЕГЭ математика профиль 2022 поможет подготовиться к единому государственному экзамену по математике, который поводится в качестве обязательного для всех выпускников средних учебных заведений, то есть школ, лицеев и гимназий.
Математика
Что представляет собой ЕГЭ математика? Данный экзамен разделён на два уровня: базовый и профильный. Первый предназначен для тех выпускников, которые не планируют продолжать обучение в вузах вовсе, а также для тех, кто поступает в вузы, где в качестве вступительных испытаний отсутствует предмет «Математика».
Профильный уровень предназначен для выпускников, планирующих продолжать обучение в высших учебных заведениях, при поступлении в которые необходимо сдавать математику.
Отыскать тренировочные варианты как базового, так и профильного уровней можно на ресурсе Решу ЕГЭ. Обновление таких вариантов происходит каждый месяц. При этом варианты составляются из новых заданий, а также тех заданий, которые оказались наиболее сложными по результатам предшествующего месяца. При желании можно обратиться не только к вариантам текущего, но и прошлых месяцев. Сделать это можно по ссылке «Прошлые месяцы». В результате откроется архив вариантов, где среди прочих представлен и 2022 год.
Решу ЕГЭ
После того как работа оказывается выполненной, система осуществляет проверку представленных ответов, показывает правильные решения, а также выставляет оценку.
Помимо тренировочных доступным является персональный вариант. Его формирование осуществляется искусственным интеллектом. Включает такой вариант 10 заданий, которые зависят от накопленной статистики. При этом учитывается текущий уровень, ранее решённые, нерешённые, а также вызвавшие затруднение задания. Для возможности выполнять задания персонального варианта требуется авторизоваться на портале Решу ЕГЭ, то есть осуществить вход в профиль. Перед этим в свою очередь необходимо выполнить регистрацию.
Для регистрации следует перейти по одноимённой ссылке, представленной в правой части веб-страницы Решу ЕГЭ. После этого будет предложено ввести свои данные. Это адрес электронной почты, который в дальнейшем будет использоваться в качестве логина. Также необходимо указать имя и фамилию. Далее следует дважды ввести пароль. Необходимо указать и дату рождения.
Регистрация
Зарегистрироваться на сайте может ученик, учитель и родитель. Пользователю необходимо выбрать подходящую ему роль. После регистрации родитель может сообщить своему ребёнку логин и попросить предоставить доступ к статистике. Это позволит получать уведомления, касающиеся домашних заданий и выставленных отметок. В том случае если дать разрешение на получение уведомлений с сайта в настройках браузера, то возможным станет получение уведомлений на своё устройство без необходимости заходить на сайт.
После того как все необходимые для регистрации данные указаны, нужно принять правила пользования сайтом и дать согласие на обработку персональных данных. Далее следует нажать на кнопку «Зарегистрироваться». В результате появится профиль на веб-ресурсе Решу ЕГЭ, вход в который можно осуществить в любое удобное для себя время.
Для того чтобы выполнить вход, потребуется указать электронную почту и пароль в специально предназначенных для этого полях в левой части сайта. После этого останется нажать на кнопку «Войти». В случае необходимости можно восстановить пароль. Для этого потребуется воспользоваться соответствующей ссылкой, после чего сообщить адрес электронной почты, который был указан в ходе регистрации, и нажать на «Отправить». После восстановления пароля можно будет осуществить вход в профиль. Выполнить вход можно и через социальную сеть ВКонтакте.
Вход в профиль
Помимо тренировочных и персонального вариантов доступным является и вариант учителя. Для того чтобы обратиться к нему, необходимо знать его номер. Такой номер следует указать в специально предназначенное для этого поле, после чего нажать на кнопку «Открыть».
Помимо прочего сайт Решу ЕГЭ позволяет осуществлять поиск в каталоге. Здесь можно искать задания демоверсий, банков пробных работ, прошедших экзаменов с решениями. Для поиска необходимо знать номер или текст задания, которые потребуется ввести в специально предназначенное для этого поле, а затем нажать на кнопку «Открыть».
Ещё одна возможность — конструктор варианта по типам и по темам, позволяющий целенаправленно тренироваться по конкретным темам. Конструктор позволяет составить вариант из нужного количества заданий, представленных в тех или иных разделах задачного каталога.
Что представляет собой базовый уровень математика 2022? Это 21 задание тестовой части, касающиеся вычислений, простейших текстовых задач, размеров и единиц измерений, чтения графиков и диаграмм, задач на квадратной решётке. Для успешной сдачи базового уровня экзамена также понадобятся знания и умения, связанные с вычислениями и преобразованиями, преобразованием выражений, простейших уравнений прикладной геометрии, начал теории вероятностей.
Базовый уровень
Среди тем представлены и выбор оптимального варианта, стереометрия, анализ графиков и диаграмм, планиметрия, неравенства, анализ утверждений, числа и свойства. Также предлагаются текстовые задачи и задачи на смекалку.
Что представляет собой ЕГЭ математика профильного уровня в 2022 году? Это 11 заданий тестовой части и 7 заданий развёрнутой. Какие именно темы охватывают задания, которые потребуется выполнить во время сдачи единого государственного экзамена?
Задания тестовой части касаются простейших уравнений, начал теории вероятностей, планиметрии, вычислений и преобразований, стереометрии, производной и первообразной, задач с прикладным содержанием, текстовых задач, графиков функций, вероятностей сложных событий, наибольшего и наименьшего значения функций.
Профильный уровень
Развёрнутая часть профильного уровня ЕГЭ математика 2022 включает уравнения, стереомерическую задачу, неравенства, финансовую математику, планиметрическую задачу, задачу с параметром, задание на числа и их свойства.
Для того чтобы подготовиться к экзамену и успешно его сдать, среди прочего сайт Решу ЕГЭ предлагает выполнять задания, представленные в вариантах Александра Ларина. Такие задания подойдут для тех, кто ищет более сложные варианты, чем обычно предлагают на ЕГЭ. На веб-ресурсе можно отыскать задания с развёрнутым ответом. Новые условия размещаются по субботам, а решения появляются по пятницам.
Таким образом, сайт Решу ЕГЭ позволяет подготовиться к экзамену по математике, выполняя задания различных вариантов. Здесь представлены как задания для тех, кто планирует сдавать базовый уровень данного предмета, так и для тех, кому необходимо сдавать профильный уровень математики для поступления в вузы.
Профильный уровень
Математика
Развёрнутая часть профильного уровня ЕГЭ математика 2022 включает уравнения, стереомерическую задачу, неравенства, финансовую математику, планиметрическую задачу, задачу с параметром, задание на числа и их свойства.
Reshu-ege. su
15.08.2020 2:28:20
2020-08-15 02:28:20
Источники:
Https://reshu-ege. su/matematika-profil-2022/
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ математика 510182
Егэ математика 510182
Егэ математика 510182
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 9 № 510281
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите больший из них.
По теореме Виета для квадратного уравнения: Таким образом, Наибольший корень
Задание 9 № 510281
—>
Егэ математика 510182.
Mathb-ege. sdamgia. ru
05.02.2017 19:25:40
2017-02-05 19:25:40
Источники:
Https://mathb-ege. sdamgia. ru/test? likes=510182