Задания
Версия для печати и копирования в MS Word
Тип 4 № 510215
Теорему косинусов можно записать в виде где a, b и c — стороны треугольника, а
— угол между сторонами a и
Пользуясь этой формулой, найдите величину
если
и
Спрятать решение
Решение.
Подставим данные величины в уравнение:
Получаем:
Ответ: 0,1
Аналоги к заданию № 509669: 510195 510215 510235 510255 520592 Все
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Решите неравенство:
Спрятать решение
Решение.
Используя свойства логарифмов, преобразуем неравенство:
Применим к последнему неравенству метод рационализации:
Решение первого неравенства: или
Из второго равенства получаем, что и
Решение третьего неравенства:
Таким образом, получаем, что решением неравенства является промежуток
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Решите неравенство:
Спрятать решение
Решение.
Используя свойства логарифмов, преобразуем неравенство:
Применим к последнему неравенству метод рационализации:
Решение первого неравенства: или
Из второго равенства получаем, что и
Решение третьего неравенства:
Таким образом, получаем, что решением неравенства является промежуток
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 4 № 510215
Теорему косинусов можно записать в виде где a, b и c — стороны треугольника, а
— угол между сторонами a и
Пользуясь этой формулой, найдите величину
если
и
Аналоги к заданию № 509669: 510195 510215 510235 510255 520592 Все
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Перейти к контенту
ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год)
|
Главная Книги — Тесты по ЕГЭ
001 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 1 002 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 2 003 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 3 004 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 4 005 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 5 006 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 6 007 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 7 008 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 8 009 ЕГЭ по математике, 11 класс. Вариант МА10209 с ответами (2019 год) — часть 9 |
ВАЖНО! Никаких реальных вариантов ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
ЗАПРЕЩЕНО копирование материалов без указания активные ссылки на источник
В случае нарушения авторских прав, правообладателям обращаться по адресу:
Контакты: tolkoexamen@gmail.com
Тест «Витамины»
Проверочная работа по биологии в 8 классе.
Консультация по физике
Онлайн-трансляция по вопросам подготовки к ЕГЭ по физике.
Наверх
ПОДЕЛИТЬСЯ
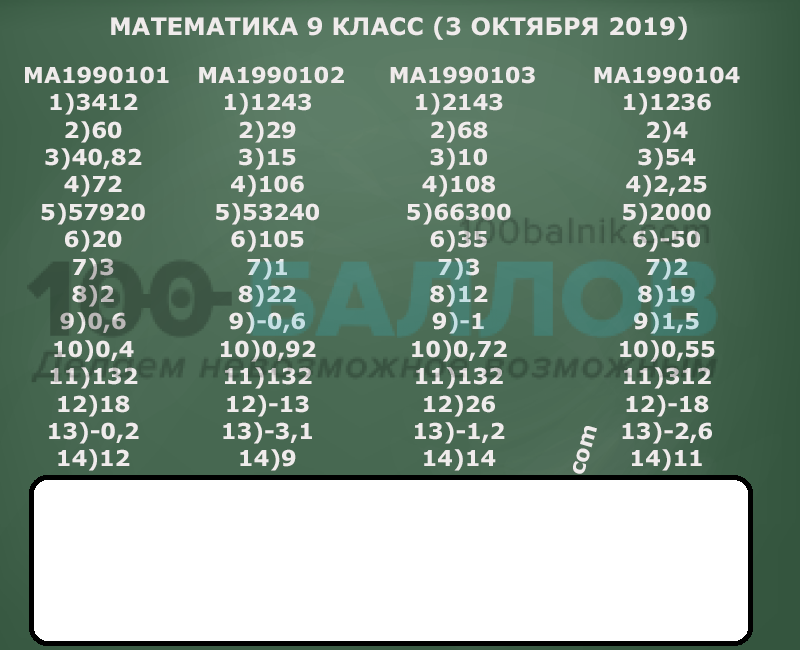
Тренировочная работа ОГЭ 2020 по математике 9 класс ответы и задания для вариантов МА1990101, МА1990102, МА1990103, МА1990104 статград 3 октября 2019-2020 учебный год.
Ответы:
Получить все ответы и сами задания математика 9 класс 3 октября 2019
Некоторые задания с работы:
1)Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом? Ответ: 60
2)Вычислите примерно площадь, которую занимают две клумбы вместе. Число p возьмите равным 3,14. Ответ: 40,82
3)Хозяин участка хочет сделать пристройку к дому. Для этого он планирует купить 12 тонн силикатного кирпича. Один кирпич весит 3 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант? Ответ: 57920
4)Баржа прошла по течению реки 72 км и, повернув обратно, прошла ещё 54 км, затратив на весь путь 9 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч
5)Углы при одном из оснований трапеции равны 53° и 37°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 2. Найдите основания трапеции.
Смотрите также ответы и задания для других тренировочных работ:
Архив работ
Диагностические и тренировочные варианты СтатГрад ЕГЭ Профиль по математике с ответамиadmin2022-03-15T16:19:09+03:00
Расписание СтатГрад 11 класс ЕГЭ 2022
Варианты 2016-2017 учебного года
22.09.2016
10109-22.09.2016
10110-22.09.2016
10111-22.09.2016
10112-22.09.2016
20.12.2016
10209-20.12.2016
10210-20.12.2016
10211-20.12.2016
10212-20.12.2016
26.01.2017
10309-26.01.2017
10310-26.01.2017
10311-26.01.2017
10312-26.01.2017
06.03.2017
10609-06.03.2017
10610-06.03.2017
10611-06.03.2017
10612-06.03.2017
21.04.2017
10709-21.04.2017
10710-21.04.2017
10711-21.04.2017
10712-21.04.2017
Варианты 2017-2018 учебного года
21.09.2017
10109-21.09.2017
10110-21.09.2017
10111-21.09.2017
10112-21.09.2017
21.12.2017
10209-21.12.2017
10210-21.12.2017
10211-21.12.2017
10212-21.12.2017
25.01.2018
10309-25.01.2018
10310-25.01.2018
10311-25.01.2018
10312-25.01.2018
06.03.2018
10409-06.03.2018
10410-06.03.2018
10411-06.03.2018
10412-06.03.2018
18.04.2018
10509-18.04.2018
10510-18.04.2018
10511-18.04.2018
10512-18.04.2018
Варианты 2018-2019 учебного года
20.09.2018
10109-20.09.2018
10110-20.09.2018
10111-20.09.2018
10112-20.09.2018
20.12.2018
10209-20.12.2018
10210-20.12.2018
10211-20.12.2018
10212-20.12.2018
24.01.2019
10309-24.01.2019
10310-24.01.2019
10311-24.01.2019
10312-24.01.2019
06.02.2019 (10 класс)
00309-06.02.2019
00310-06.02.2019
13.03.2019
10409-13.03.2019
10410-13.03.2019
10411-13.03.2019
10412-13.03.2019
19.04.2019
10509-19.04.2019
10510-19.04.2019
10511-19.04.2019
10512-19.04.2019
24.04.2019 (Итоговая контрольная работа Профильный уровень 10 класс)
00403-24.04.2019
00404-24.04.2019
17.05.2019 (10-11 класс)
00509-17.05.2019
00510-17.05.2019
00511-17.05.2019
00512-17.05.2019
Варианты 2019-2020 учебного года
25.09.2019
1910109-25.09.2019
1910110-25.09.2019
1910111-25.09.2019
1910112-25.09.2019
18.12.2019
1910209-18.12.2019
1910210-18.12.2019
1910211-18.12.2019
1910212-18.12.2019
29.01.2020
1910309-29.01.2020
1910310-29.01.2020
1910311-29.01.2020
1910312-29.01.2020
06.02.2020 (10 класс)
1900209-06.02.2020
1900210-06.02.2020
12.02.2020 (10 класс Тригонометрия)
1900403-12.02.2020
1900404-12.02.2020
11.03.2020
1910409-11.03.2020
1910410-11.03.2020
1910411-11.03.2020
1910412-11.03.2020
02.04.2020 (10 класс Теория вероятностей и статистика)
1900503-02.04.2020
1900504-02.04.2020
15.04.2020 (10 класс Итоговая уровневая работа)
1900603-15.04.2020
1900604-15.04.2020
22.04.2020
1910509-22.04.2020
1910510-22.04.2020
1910511-22.04.2020
1910512-22.04.2020
15.05.2020
1900709-15.05.2020
1900710-15.05.2020
Варианты 2020-2021 учебного года
30.09.2020
2010109-30.09.2020
2010110-30.09.2020
2010111-30.09.2020
2010112-30.09.2020
16.12.2020
2010209-16.12.2020
2010210-16.12.2020
2010211-16.12.2020
2010212-16.12.2020
28.01.2021 (10 класс)
2000309-28.01.2021
2000310-28.01.2021
10.02.2021
2010309-10.02.2021 [с видео-разбором]
2010310-10.02.2021
2010311-10.02.2021
2010312-10.02.2021
16.03.2021
2010409-16.03.2021
2010410-16.03.2021
2010411-16.03.2021
2010412-16.03.2021
29.04.2021
2010509-29.04.2021 [с видео-разбором]
2010510-29.04.2021
2010511-29.04.2021
2010512-29.04.2021
13.05.2021
2000709-13.05.2021
2000710-13.05.2021
Варианты 2021-2022 учебного года
28.09.2021
2110109-28.09.2021
2110110-28.09.2021
2110111-28.09.2021
2110112-28.09.2021
15.12.2021
2110209-15.12.2021
2110210-15.12.2021
2110211-15.12.2021
2110212-15.12.2021
27.01.2022 (10-11 класс)
2100109-27.01.2022
2100110-27.01.2022
16.02.2022
2110309-16.02.2022
2110310-16.02.2022
2110311-16.02.2022
2110312-16.02.2022
15.03.2022
2110409-15.03.2022
2110410-15.03.2022
2110411-15.03.2022
2110412-15.03.2022
К пищеварительному каналу относят
- печень
- ротовую полость
- пищевод и желудок
- поджелудочную железу
- слюнные железы
- слепую кишку
📜Теория для решения:
Пищеварительная система
Посмотреть решение
Раз это канал, то, видимо, по нему пища проходит свой путь от попадания в рот и до дефикации.
Пусть мы не знаем достоверно, что происходит с пищей. Во-первых, она попадает в рот, затем, наверно, всем известно, она попадает в желудок и кишечник, который, в свою очередь, делится на толстый и тонкий.
Выберем варианты: ротовая полость, желудок и пищевод, кишка, в вариантах представлена слепая кишка.
Что же касается печени и слюнных желез и поджелудочной, то в них пища не попадает. Печень хотя бы орган, а железы вообще занимаются секрецией, в них даже трудно представить, чтобы что-то попадало.
Ответ: 236
Ксения Алексеевна | Просмотров: 393
| 1360 | Дан треугольник ABC со сторонами AB=20, AC=12, BC=16. Точки M и N — середины сторон AB и АС соответственно. а) Докажите, что окружность, вписанная в треугольник ABC касается одной из средних линий. б) Найдите общую хорду окружности, одна из которых вписана в треугольник ABC, а вторая описана около треугольника AMN |
Тренировочная работа №2 20.12.2018 СтатГрад ЕГЭ 11 класс профильный уровень Задание 16 (Вариант МА10209) |
|
| 1357 | Найдите все значения a, при которых система {(y=(a+2)x^2+2ax+a-1) , (x=(a+2)y^2+2ay+a-1) :} имеет ровно одно решение |
Тренировочная работа №2 20.12.2018 СтатГрад ЕГЭ 11 класс профильный уровень Задание 18 (Вариант МА10209) |
|
| 1355 | а) Решите уравнение 7/(1-cos^2(x))+9/sin(x)=10 б) Укажите корни этого уравнения, принадлежащие отрезку [-3pi; -(3pi)/2]. |
Тренировочная работа №2 20.12.2018 СтатГрад ЕГЭ 11 класс профильный уровень Задание 13 (Вариант МА10209) |
|
| 1354 | В правильной треугольной пирамиде MABC боковые рёбра равны 10, а сторона основания равна 12. Точки G и F делят стороны основания AB и AC соответственно так, что AG:GB=AF:FC=1:5. а) Докажите, что сечение пирамиды плоскостью MGF является равнобедренным треугольником. б) Найдите площадь сечения пирамиды плоскостью MGF |
Тренировочная работа №2 20.12.2018 СтатГрад ЕГЭ 11 класс профильный уровень Задание 14 (Вариант МА10209) |
|
| 1353 | Решите неравенство 4^(x-3)-2^(x-3)*(16-x^2)-16x^2>=0 |
Тренировочная работа №2 20.12.2018 СтатГрад ЕГЭ 11 класс профильный уровень Задание 15 (Вариант МА10209) |
|
| Clear |
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Финансовый консультант Марти Бёрд вместе с женой Вэнди и остальными членами семьи вынужден тайно переехать из престижного предместья Чикаго в курортный городок Озарк штата Миссури. К неожиданному переезду главного героя вынудили крупные долги, и на новом месте он надеется поправить своё финансовое положение.
- Название: Ozark
- Год выхода: 2017-07-21
- Страна: США
- Режиссер: Джейсон Бейтман, Алик Сахаров, Аманда Марсалис
- Статус сериала: Завершен
- Перевод: Пифагор
- Качество: FHD (1080p) (60 мин)
- Возраст: Сериал для зрителей старше 16+ лет
-
7.9
8.4
- В главных ролях: Джейсон Бейтман, Лора Линни, София Хьюблиц, Скайлар Гертнер, Джулия Гарнер, Лиза Эмери, Чарли Тахэн, Кевин Л. Джонсон, Джордана Спиро, Джейсон Батлер Харнер
- Подборки: Netflix, Про мафию, банды
- Жанры: Криминал, Триллер, Зарубежный, Драма
4 сезон 14 серия
Озарк смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет