Найдите все значения a, при каждом из которых уравнение
имеет более двух корней.
Спрятать решение
Решение.
Преобразуем исходное уравнение:
Последнее уравнение имеет более двух корней или если a = −1, или если уравнение имеет два различных корня, отличных от 3:
откуда или
Исходное уравнение имеет более двух различных корней при при a = −1, при
и при
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| Обоснованно получены все значения: |
3 |
| Обоснованно получено одно, два или три из значений |
2 |
| Задача верно сведена к исследованию
— графиков функций, заданных выражениями, стоящими в левой и правой части равенства; — квадратных уравнений, полученных после раскрытия модулей |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Источник: ЕГЭ — 2014. Основная волна.
Эффективная подготовка к ЕГЭ
Параметры (С6)
Опубликовано ср, 09/21/2016 — 21:57 пользователем DmitryM
Все номера с портала Д.Гущина reshuege.ru
I Графическое решение
1 484650, 484649,
2
Дома 509931
3
507648=510583, дома
4 Полоса+ окружность 509026
5 Система прямых
509825
Дома 510571
Найдите все значения при каждом из которых график функции
пересекает ось абсцисс более чем в двух различных точках.
Источник: МИОО: Тренировочная работа по математике 2010 год вариант 201. (Часть С)
Найдите все значения a, при каждом из которых график функции
пересекает ось абсцисс менее чем в трех различных точках.
Задание 18 № 507578
Найдите все такие значения параметра , при каждом из которых уравнение
имеет хотя бы одно решение.
Задание 18 № 509047
Найдите все значения a, при каждом из которых система уравнений
имеет ровно два различных решения.
Задание 18 № 509206
Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.
1 Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.
Задание 18 № 507589
Источник: МИОО: Диагностическая работа 08.12.2009 вариант 1 (Часть С).
2 Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.
Источник: МИОО: Диагностическая работа 08.12.2009 вариант 2 (Часть С).
Окружность + пересечение двух парабол с ветвями вверх и вниз:
1 Найдите все значения параметра а, при каждом из которых система имеет ровно 4 решения.
Задание 18 № 507709
2
Найдите все значения параметра а, при каждом из которых система имеет ровно 8 решений.
адание 18 № 484648
3
Найдите все значения параметра при каждом из которых система
имеет ровно решений.
адание 18 № 484646
Показать решение
Похоже, но окружность + четырехугольник
1
Найдите все значения параметра а, при каждом из которых система уравнений имеет
а) ровно четыре решения,
б) ровно 8 решений.дание 18 № 484642
2
Найдите все значения параметра при каждом из которых система уравнений
имеет ровно четыре решения.
Задание 18 № 484641
Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.
Задание 18 № 507589
Источник: МИОО: Диагностическая работа 08.12.2009 вариант 1 (Часть С).
Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.
Задание 18 № 507594
Источник: МИОО: Диагностическая работа 08.12.2009 вариант 2 (Часть С).
Показать решение
Найдите все значения при каждом из которых множеством решений неравенства
является отрезок.
Задание 18 № 510547
Источник: МИОО: Диагностическая работа по математике 17.02.2010 с решениями: вариант 2 (Часть С).
Показать решение
Найдите все значения параметра при каждом из которых неравенство
имеет единственное целое решение.
Задание 18 № 510559
Источник: МИОО: Диагностическая работа по математике 20.10.2010 вариант 4. (Часть С)
II Свойства функций
1 Задание 18 № 485938.
Найдите все значения $a$, при которых наименьшее значение функции
$$ f(x) =4ax +|x^2 — 6x +5| $$
больше, чем -24.
Аналоги к заданию № 485938: 485946 485953 500819 503150 № 511452
Найдите все значения a, для каждого из которых существует хотя бы одна пара чисел x и y, удовлетворяющих неравенству
Задание 18 № 503324
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 701.
Найдите все значения параметра из интервала
, при каждом из которых система уравнений
имеет единственное решение.
Задание 18 № 514049
III Преобразования
3.1
Задание 18 № 514129. Найдите все значения a, при которых уравнение
имеет единственное решение.
Источник: Задания 18 (С6) ЕГЭ 2014
3.2
Задание 18 № 512875. Найдите все значения a, при каждом из которых уравнение
имеет более двух корней.
Источник: ЕГЭ — 2014. Основная волна.
3.3
Найти все значения при каждом из которых функция
имеет более двух точек экстремума.
Задание 18 № 484644
Найдите все значения a, при каждом из которых функция
имеет более двух точек экстремума.
Задание 18 № 507185
Аналоги к заданию № 507185: 507186 507187 507188 507189 507191
3.4
Найдите все значения а, при каждом из которых наименьшее значение функции
на множестве не менее 6.
Задание 18 № 500016
5
Найдите все значения a, при каждом из которых наименьшее значение функции
на множестве не меньше 6.
Найдите все значения a, при которых уравнение
имеет ровно два различных корня.
Задание 18 № 512886
Источник: ЕГЭ — 2014. Основная волна. Вариант 801.
6
Найдите все значения a, при которых уравнение
имеет ровно два различных корня.
Задание 18 № 512892
Источник: ЕГЭ — 2014. Основная волна. Вариант 802.
Найдите все значения a, при каждом из которых уравнение
имеет единственный корень.
Задание 18 № 501693
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 1.
26
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Задание 18 № 501733
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Урал. Вариант 203.
Найдите все значения a, при каждом из которых уравнение
имеет хотя бы один корень.
Задание 18 № 503256
Источник: ЕГЭ по математике 23.04.2013. Досрочная волна. Восток. Вариант 1.
Найдите все значения параметра а, при каждом из которых множество значений функции содержит отрезок
Задание 18 № 507891
Источник: СтатГрад: Диагностическая работа по математике 21.01.2015 вариант МА10109.
Найдите все значения а, при каждом из которых уравнение
имеет ровно три различных корня.
Задание 18 № 514538
Источник: ЕГЭ — 2016 по математике. Основная волна 06.06.2016. Вариант 3 (C часть)
Найдите все значения а, при каждом из которых уравнение
имеет ровно три различных решения.
Задание 18 № 514451
Источник: Задания 18 (С6) ЕГЭ 2016
Найдите все значения , при каждом из которых неравенство
выполняется при всех
Задание 18 № 500115
Аналоги к заданию № 500115: 511336
Найдите все значения a, при каждом из которых функция
имеет более двух точек экстремума.
Аналоги к заданию № 507185: 507186 507187 507188 507189 507191
Найти все значения параметра при каждом из которых среди значений функции
есть ровно одно целое число.
Задание 18 № 507743
Источник: МИОО: Тренировочная работа по математике 2010 год вариант 501. (Часть С)
IV Единственное решение
Найдите все неотрицательные значения a, при каждом из которых множество решений неравенства
состоит из одной точки, и найдите это решение.
Задание 18 № 513282
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
Copyright © 2023,
Developed by Devsaran.
Целое рациональное
число 512875
– составное.
28 — сумма цифр данного числа.
16 — количество делителей.
Их сумма: 700128.
512875 и 0.000001949792834511333 являются взаимно обратными числами.
Другие представления числа 512875:
двоичный вид числа: 1111101001101101011, троичный вид числа: 222001112101, восьмеричный вид числа: 1751553, шестнадцатеричный вид числа: 7D36B.
Конвертация из числа байтов — 500 килобайтов 875 байтов .
Число 512875 азбукой Морзе: ….. .—- ..— —.. —… …..
Косинус числа 512875: -0.8395, синус числа 512875: -0.5434, тангенс числа 512875: 0.6474.
Логарифм натуральный: 13.1478.
Логарифм десятичный числа 512875 равен 5.7100.
716.1529 — корень квадратный, 80.0455 — кубический.
Возведение в квадрат: 2.6304e+11.
Число 512875 в секундах это 5 дней 22 часа 27 минут 55 секунд .
Цифра 1 — это нумерологическое значение этого числа.
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна $$6sqrt{6}$$, $$BH=3$$ Найдите $$cos BAC$$.
Ответ: 0,2
Скрыть
Задание 2
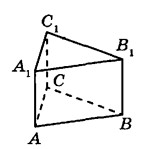
Найдите объём многогранника, вершинами которого являются точки $$B$$, $$C$$, $$A_1$$, $$C_1$$ правильной треугольной призмы $$ABCA_1B_1C_1$$ площадь основания которой равна 5, а боковое ребро равно 6.
Ответ: 10
Скрыть
Задание 3
В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист 3. полетит третьим рейсом вертолёта.
Ответ: 0,2
Скрыть
Номер рейса в этой задаче не имеет значения. Важно, что за один рейс перевозятся 5 человек. То есть, вероятность попасть туристу З. на какой-либо рейс (в том числе и 3-й), равна:
$$P=frac{m}{n}=frac{5}{25}=frac{1}{5}=0,2$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 5. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,56
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{4})^{x+2}=256^{x}$$
Ответ: -0,4
Скрыть
Задание 6
Найдите значение выражения $$log_{2,5}6cdot log_{6} 0,4$$
Ответ: -1
Скрыть
Задание 7
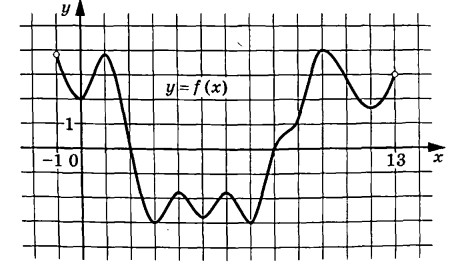
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-1; 13)$$. Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-2$$.
Ответ: 9
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$y=1,4+11t-5t^2$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 0,6
Скрыть
Задание 9
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси? Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 55
Скрыть
Задание 10
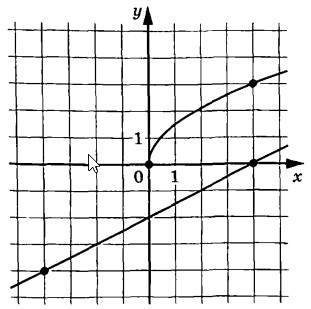
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точке $$A(x_0; y_0)$$. Найдите $$y_0$$.
Ответ: 6
Скрыть
Задание 11
Найдите точку максимума функции промежутку $$y=(2x-1)cos x-2sin x+9$$, принадлежащую промежутку $$(0;frac{pi}{2})$$
Ответ: 0,5
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(4x^{2})+3log_{0,5}(8x)=1$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0,15;1,5]$$
Ответ: а)$$0,25;sqrt[4]{8}$$ б)$$0,25$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$. Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что $$M$$ — середина $$SB$$.
б) Найдите расстояние между прямыми $$AC$$ и $$DM$$, если высота пирамиды равна $$6sqrt{3}$$.
Ответ: 3
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x+4}(8-3^{2+x^{2}})}{4^{x-1}-3}leq 0$$
Ответ: $$-4;(log_{4}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей.
Ответ: 8 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной из вершины $$C$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что $$I$$ и $$J$$ лежат на отрезке $$EF$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=15$$, $$BC = 20$$.
Ответ: $$6sqrt{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{2}=|x|$$ и $$asqrt{2}+x=sqrt{2asqrt{2}-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$[sqrt{2};frac{3sqrt{6}}{sqrt{13}})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 68?
б) Может ли $$n$$ равняться 86?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)79
Скрыть
Тип 1 № 368401
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Качели | Поле для мини‐ футбола |
Верёвочный комплекс |
Песочница |
|---|---|---|---|---|
| Цифры |
На плане (см. рис.) изображена детская площадка, расположенная в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на плане равна 1 м). Площадка предназначена как для детей младшего возраста, так и для школьников, поэтому она разделена на две отдельные части. При этом по краю зоны для малышей есть специальная дорожка, по которой можно кататься на роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс — самую маленькую.
2. Тип 2 № 368402
Сколько кубических метров песка понадобилось, чтобы слой песка в песочнице был 20 см?
3. Тип 3 № 368403
Найдите площадь (в м2), игрового комплекса для малышей.
4. Тип 4 № 368404
Найдите длину (в метрах) диагонали поля для мини‐футбола.
5. Тип 5 № 368406
Жители домов тщательно изучили современные материалы для мощения детской площадки. Было решено уложить в тех зонах, где есть риск получить травму, современное резиновое бесшовное покрытие. Такими зонами оказались площадка для малышей (за исключением песочницы, но включая дорожку), комплекс уличных тренажёров, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. Цены на материалы и монтаж приведены в таблице.
| Площадь (м2) | менее 100 | 100‐250 | 250‐500 | более 500 |
|---|---|---|---|---|
| Цена (руб./м2) | 1500 | 1470 | 1430 | 1400 |
Заказ на все площадки делается одновременно, и стоимость заказа зависит от суммарной площади. На сколько рублей дороже оказалось покрыть площадку для малышей, чем площадку для школьников?
6. Тип 6 № 314262
Вычислите:
7. Тип 7 № 322419
На координатной прямой отмечены числа p, q и r.
Какая из разностей p − r, p − q, r − q отрицательна?
В ответе укажите номер правильного варианта.
1) p − r
2) p − q
3) r − q
4) ни одна из них
8. Тип 8 № 370465
Найдите значение выражения
9. Тип 9 № 338915
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Тип 10 № 311336
В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
11. Тип 11 № 316368
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
В)
ГРАФИКИ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Тип 12 № 338056
Закон всемирного тяготения можно записать в виде где F — сила притяжения между телами (в ньютонах),
и
— массы тел (в килограммах), r — расстояние между центрами масс (в метрах), а
— гравитационная постоянная, равная 6,67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела
(в килограммах), если
Н,
кг, а
м.
13. Тип 13 № 339292
На каком рисунке изображено множество решений неравенства
В ответе укажите номер правильного варианта.
| 1)
|
2)
|
| 3)
|
4)
|
14. Тип 14 № 393948
Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
15. Тип 15 № 132773
Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
16. Тип 16 № 348961
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 6,5. Найдите AC, если
17. Тип 17 № 323436
Найдите площадь треугольника, изображённого на рисунке.
18. Тип 18 № 348499
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
19. Тип 19 № 348369
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
20. Тип 20 № 353544
Решите систему неравенств
21. Тип 21 № 338603
Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
22. Тип 22 № 153
Постройте график функции и определите, при каких значениях k прямая
имеет с графиком ровно одну общую точку.
23. Тип 23 № 311566
Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника.
24. Тип 24 № 311608
Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
25. Тип 25 № 315126
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Просмотр содержимого документа
«2023 ОГЭ Январь Математика Вариант 5»
На экранах долгожданный шестой сезон одного из самых популярных и востребованных сериалов на зарубежном телевидении. Проект «Викинги» повествует о выдающемся воинственном народе, который проживает в Скандинавии и управляется безумным, яростным, но при этом очень мудрым правителем Рагнаром Лодброком. Этот человек смог собрать вокруг себя верных людей, смог установить свои правила на родных территориях, а вскоре отправился на покорение европейских земель. Главный герой повёл за собой свою армию, которая дошла с ним до территории Франции, осадив Париж и забрав сокровища одной из самых могущественных стран центральной Европы! Викингам по силам оказалось разбить армии англичан, которых не спасло даже нахождение на море. Ко всему прочему, главные персонажи сумели пробиться вглубь континента, наворотив дел и в других частях Европы.Продолжение истории обещает зрителям ещё более интересные походы. В этот раз главный герой вместе с верными товарищами отправится на восточные земли. Его встреча с Вещим Олегом, роль которого исполнит великолепный российский актёр Данила Козловский будет судьбоносной. Но чем же обернётся новый сезон знаменитого сериала?
- Название: Vikings
- Год выхода: 2013-03-03
- Страна: Канада, Ирландия
- Режиссер: Киаран Доннелли, Кен Джиротти, Стивен Ст.
- Статус сериала: Завершен
- Перевод: LostFilm
- Качество: FHD (1080p) (45 мин)
- Возраст: Сериал для зрителей старше 18+ лет
-
8.2
8.5
- В главных ролях: Кэтрин Уинник, Густаф Скарсгард, Александр Людвиг, Джорджия Хёрст, Алекс Хег Андерсен, Джордан Патрик Смит, Марко Ильсё, Петер Францен, Трэвис Фиммел, Клайв Стэнден
- Жанры: Приключения, Военный, Исторический, Боевик, Мелодрама, Драма
6 сезон 21 серия
Викинги смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет
К сожалению некоторые диалоги в сериале не переведены, рекомендуем в настройках включить субтитры, чтобы понимать диалоги. Приятного просмотра!
12-е задание: «Алгоритмы с циклами и условиями»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Умение анализировать результат исполнения алгоритма
До ЕГЭ 2021 года — это было задание № 14 ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Содержание:
- Исполнитель Редактор и цепочки символов
- Какая строка получится?
- Сколько удалено?
- Чему равна сумма цифр?
- Сколько цифр … в конечной строке?
- Сколько цифр … в исходной строке?
- Укажите минимальную возможную длину входной строки
- Какое наибольшее / наименьшее количество … могло быть в исходной строке?
- Решение заданий прошлых лет (до 2021)
- Исполнитель Робот
- Исполнитель Чертежник
Исполнитель Редактор и цепочки символов
Учимся по видео (решения разного типа программным способом):
📹 YouTube здесь
Какая строка получится?
12_4:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Б) нашлось (v)
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 40 идущих подряд цифр 123? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (12) ИЛИ нашлось (333)
ЕСЛИ нашлось (12)
ТО заменить (12, 3)
ИНАЧЕ заменить (333, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Ответ: 33
📹 Видео (Теоретическое)
✍ Показать решение:
✎ Решение 1. Теоретическое:
- Рассмотрим алгоритм: редактор будет выполнять команды только тогда, когда в строке встречается цепочка «12» или цепочка «333»;
- если в строке есть «12», то тогда эта цепочка заменяется на «3»;
- если в строке нет цепочки «12», но есть «333», то цепочка «333» заменяется на «3».
- Теперь вернемся к условию нашей задачи. Условие цикла истинно, соответственно выполняем блок ЕСЛИ, т.е. делаем замену: в каждом из 40 чисел ‘123‘, заменяем 12 на 3. Получим 40 + 40 = 80 троек (40 троек было изначально и 40 добавилось);
123123123...123 ↓ ↓ ↓ ↓ 3 33 33 3...3 3
333 333 333 333... 333 33 26 троек по три получили: 3 3 3 3 ... 3 33 26 + 2
333 333 333 333... 333 3 9 троек по три + 1 получили: 3 3 3 3 ... 3 3 9 + 1
333 333 333 3 3 тройки по три + 1 получили: 3 3 3 3
3 3 3 3 ↓ 3 3
Результат: 33
✎ Решение 2. Программное:
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 |
begin var s := '123' * 40; while ('12' in s) or ('333' in s) do begin if '12' in s then s := s.Replace('12', '3', 1) else s := s.Replace('333', '3', 1); end; print(s); end. |
Pascal (традиционный):
begin var s := '123'*40; var p1 := Pos('12',s); var p2 := Pos('333',s); while (p1 > 0) or (p2 > 0) do begin if p1 > 0 then begin Delete( s, p1, 2 ); Insert( '3', s, p1 ); end else begin Delete( s, p2, 3 ); Insert( '3', s, p2 ); end; p1 := Pos('12',s); p2 := Pos('333',s); end; write(s); end. |
Python:
s = 40*'123' while "12" in s or "333" in s: if "12" in s: s = s.replace( "12", "3", 1 ) else: s = s.replace( "333", "3", 1 ) print(s) |
С++:
#include<iostream> using namespace std; int main() { string s(40, '123'); cout << s << endl; int p1 = s.find("12"); int p2 = s.find("333"); while( p1 != string::npos or p2 != string::npos ) { if( p1 != string::npos ) s.replace( p1, 12, "3" ); else s.replace( p2, 333, "3" ); p1 = s.find("12"); p2 = s.find("333"); cout << s << endl; } cout << s; } |
12_5:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Б) нашлось (v)
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 71 идущих подряд четверок цифр 1122? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (12) ИЛИ нашлось (222)
ЕСЛИ нашлось (12)
ТО заменить (12, 2)
ИНАЧЕ заменить (222, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Ответ: 22
✍ Показать решение:
✎ Решение 1. Теоретическое:
- Для удобства решения сначала сократим исходную цепочку до одной группы цифр:
1122
1122 => 122
122 => 22
71 * 2 = 142 двойки из 71 группы
142 / 3 = 47 двоек + 1 двойка (остаток) = 48 двоек
48 / 3 = 16 двоек
16 / 3 = 5 двоек + 1 двойка (остаток) = 6 двоек
6 / 3 = 2 двойки
✎ Решение 2. Программное:
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 |
begin var s := '1122' * 71; while ('12' in s) or ('222' in s) do begin if '12' in s then s := s.Replace('12', '2', 1) else s := s.Replace('222', '2', 1); end; print(s); end. |
Pascal (традиционный):
begin var s := '1122'*71; var p1 := Pos('12',s); var p2 := Pos('222',s); while (p1 > 0) or (p2 > 0) do begin if p1 > 0 then begin Delete( s, p1, 2 ); Insert( '2', s, p1 ); end else begin Delete( s, p2, 3 ); Insert( '2', s, p2 ); end; p1 := Pos('12',s); p2 := Pos('222',s); end; write(s); end. |
Python:
s = 71*'1122' while "12" in s or "222" in s: if "12" in s: s = s.replace( "12", "2", 1 ) else: s = s.replace( "222", "2", 1 ) print(s) |
С++:
#include<iostream> using namespace std; int main() { string s(71, '1122'); cout << s << endl; int p1 = s.find("12"); int p2 = s.find("222"); while( p1 != string::npos or p2 != string::npos ) { if( p1 != string::npos ) s.replace( p1, 12, "2" ); else s.replace( p2, 222, "2" ); p1 = s.find("12"); p2 = s.find("222"); cout << s << endl; } cout << s; } |
12_6:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Б) нашлось (v)
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 200 идущих подряд цифр 7? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (99) ИЛИ нашлось (777)
ЕСЛИ нашлось (777)
ТО заменить (777, 9)
ИНАЧЕ заменить (99, 7)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Типовые задачи для тренировки
Ответ: 977
📹 Видео (Теоретическое)
✍ Показать решение:
- Рассмотрим алгоритм: редактор будет выполнять команды только тогда, когда в строке встречается цепочка «99» или цепочка «777»;
- если в строке есть «777», то тогда эта цепочка заменяется на «9»;
- если в строке нет цепочки «777», но есть «99», то цепочка «99» заменяется на «7».
- Теперь вернемся к условию нашей задачи. Условие цикла истинно, условие ЕСЛИ нашлось 777 тоже истинно, делаем замену:
- сколько раз можно заменить в 200 семерках три семерки на одну девятку? 200 делим на 3 получаем 66 замен, т.е. 66 цифр «9» + 2 семерки в остатке;
777 777 ... 777 77 получили: 9...9 77 ↓ 66
66 цифр 99 999...999 77 ↓ 7 999...999 77 64 цифры
64 цифры 799 999...999 77 ↓ 77 999...999 77 62 цифры
62 цифры 7799 999...999 77 ↓ 777 999...999 77 60 цифр
60 цифр 777 999...999 77 ↓ 9 999...999 77 61 цифра
61 : 5 = 12 раз 12 раз возможно отнять по 5 девяток и 1 девятка останется "в остатке"
12_7:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Б) нашлось (v)
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 90 идущих подряд цифр 3 и в конце одной цифры 1? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (331) ИЛИ нашлось (166)
ЕСЛИ нашлось (331)
ТО заменить (331, 16)
ИНАЧЕ заменить (166, 31)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Ответ: 316
📹 Видео (Теоретическое)
✍ Показать решение:
-
✎ Решение 1. Программное:
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 |
begin var s := '3' * 90 + '1'; while ('331' in s) or ('166' in s) do begin if '331' in s then s := s.Replace('331', '16', 1) else s := s.Replace('166', '31', 1); end; print(s); end. |
Pascal (традиционный):
begin var s := '3'*90 + '1'; var p1 := Pos('331',s); var p2 := Pos('166',s); while (p1 > 0) or (p2 > 0) do begin if p1 > 0 then begin Delete( s, p1, 3 ); Insert( '16', s, p1 ); end else begin Delete( s, p2, 3 ); Insert( '31', s, p2 ); end; p1 := Pos('331',s); p2 := Pos('166',s); end; write(s); end. |
Python:
s = 90*'3'+'1' while "331" in s or "166" in s: if "331" in s: s = s.replace( "331", "16", 1 ) else: s = s.replace( "166", "31", 1 ) print(s) |
С++:
#include<iostream> using namespace std; int main() { string s(90, '3'); s+='1'; cout << s << endl; int p1 = s.find("331"); int p2 = s.find("166"); while( p1 != string::npos or p2 != string::npos ) { if( p1 != string::npos ) s.replace( p1, 331, "16" ); else s.replace( p2, 166, "31" ); p1 = s.find("331"); p2 = s.find("166"); cout << s << endl; } cout << s; } |
Сколько удалено?
12_8:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Б) нашлось (v)
Дана программа для исполнителя Редактор:
ПОКА нашлось (555) ИЛИ нашлось (333)
ЕСЛИ нашлось (333)
ТО заменить (333, 5)
ИНАЧЕ заменить (555, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
Дана строка, состоящая из 500 цифр 5. Сколько пятёрок было удалено за время обработки строки по этой программе?
Ответ: 561
✍ Показать решение:
✎ Решение 1. Теоретическое:
- Выполним несколько итераций цикла ПОКА. Когда мы получим ту же самую последовательность цифр пять, за исключением их количества — остановимся:
5..5 500шт 1: Работает блок ИНАЧЕ (555->3): 35..5 497шт 2: Работает блок ИНАЧЕ (555->3): 335..5 494шт 3: Работает блок ИНАЧЕ(555->3): 3335..5 491шт 4: Работает блок ЕСЛИ (333->5): 5..5 492шт
500 - 492 = 8. Посчитаем, сколько раз можно выполнить данный фрагмент:500 : 8 = 62 и 4 в остатке
62 * 9 = 558
Работает блок ИНАЧЕ(555->3):
5555 = 35
558 + 3 = 561
✎ Решение 2. Программное:
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
begin var s := '5' * 500; var k := 0; while ('555' in s) or ('333' in s) do begin if '333' in s then s := s.Replace('333', '5', 1) else begin s := s.Replace('555', '3', 1); k += 3; end; end; print(k); end. |
Pascal (традиционный):
begin var k:= 0; var s := '5'*500 ; var p1 := Pos('555',s); var p2 := Pos('333',s); while (p1 > 0) or (p2 > 0) do begin if p2 > 0 then begin Delete( s, p2, 3 ); Insert( '5', s, p2 ); end else begin Delete( s, p1, 3 ); Insert( '3', s, p1 ); inc(k,3); end; p1 := Pos('555',s); p2 := Pos('333',s); end; write(k); end. |
Python:
s = 500*'5' k=0 while "555" in s or "333" in s: if "333" in s: s = s.replace( "333", "5", 1 ) else: s = s.replace( "555", "3", 1 ) k+=3; print(k) |
С++:
#include<iostream> using namespace std; int main() { string s(500, '5'); int k = 0; cout << s << endl; int p1 = s.find("555"); int p2 = s.find("333"); while( p1 != string::npos or p2 != string::npos ) { if( p2 != string::npos ) s.replace( p2, 333, "5" ); else { s.replace( p1, 555, "3" ); k+=2; } p1 = s.find("555"); p2 = s.find("333"); cout << s << endl; } cout << k; } |
📹 Видео (Теоретическое)
Чему равна сумма цифр?
12_13:
Дана программа для исполнителя Редактор:
ПОКА нашлось (555) ИЛИ нашлось (333)
ЕСЛИ нашлось (555)
ТО заменить (555, 3)
ИНАЧЕ заменить (333, 5)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
Дана строка, состоящая из 200 цифр 5. Чему равна сумма цифр строки, полученной после обработки по этой программе?
Ответ: 16
Показать решение:
-
✎ Решение 1. Программное:
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
begin var s := '5' * 200; while ('555' in s) or ('333' in s) do begin if '555' in s then s := s.Replace('555', '3', 1) else s := s.Replace('333', '5', 1) end; println(s); var sum := s.CountOf('5') * 5 + s.CountOf('3') * 3; print(sum) end. |
| Pascal (традиционный): | |
| Python: | С++: |
12_9:
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 10 цифр 1, 20 цифр 2 и 30 цифр 3, расположенных в произвольном порядке.
Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы.
Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
НАЧАЛО ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3) ЕСЛИ нашлось (>1) ТО заменить (>1, 22>) КОНЕЦ ЕСЛИ ЕСЛИ нашлось (>2) ТО заменить (>2, 2>) КОНЕЦ ЕСЛИ ЕСЛИ нашлось (>3) ТО заменить (>3, 1>) КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ
Ответ: 110
📹 Видео (Теоретическое)
Показать решение:
✎ Решение 1. Программное:
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
begin var s := '>' + '1' * 10 + '2' * 20 + '3' * 30; var k := 0; while ('>1' in s) or ('>2' in s) or ('>3' in s) do begin if '>1' in s then s := s.Replace('>1', '22>', 1); if '>2' in s then s := s.Replace('>2', '2>', 1); if '>3' in s then s := s.Replace('>3', '1>', 1); end; var sum := s.CountOf('1') + s.CountOf('2') * 2 + s.CountOf('3') * 3; {или так: var sum: integer; for var i := 1 to s.Count do if (s[i]='1') or (s[i]='2') or(s[i]='3') then sum:=sum + StrToInt(s[i]); } print(sum) end. |
Pascal (традиционный):
|
||
| Python: | С++: |
Сколько цифр … в конечной строке?
12_10:
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (12) ИЛИ нашлось (1)
ЕСЛИ нашлось (12)
ТО заменить (12, 2221)
ИНАЧЕ заменить (1,222222)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей одной единицы и 51 стоящих справа от неё цифр 2? В ответ, запишите, сколько цифр 2 будет в конечной строке.
Ответ: 159
Показать решение:
-
✎ Решение 1. Программное:
PascalABC.net:
1 2 3 4 5 6 7 8 9 10 11 |
begin var s := '1' + '2' * 51; while ('12' in s) or ('1' in s) do begin if '12' in s then s := s.Replace('12', '2221', 1) else s := s.Replace('1', '222222', 1); end; print(s.CountOf('2')) end. |
Pascal (традиционный):
|
||
| Python: | С++: |
Сколько цифр … в исходной строке?
12_14:
Дана программа для Редактора:
ПОКА нашлось(01) ИЛИ нашлось(02) ИЛИ нашлось(03) заменить(01, 30) заменить(02, 3103) заменить(03, 1201) КОНЕЦ ПОКА
Известно, что исходная строка начиналась с нуля, а далее содержала только единицы, двойки и тройки. После выполнения данной программы получилась строка, содержащая 31 единицу, 24 двойки и 46 троек. Сколько троек было в исходной строке?
Ответ: 17
Показать решение:
-
✎ Решение 1. Программное:
PascalABC.net:
|
||
Python:
for n1 in range(50): for n2 in range(50): for n3 in range(50): # зададим исходную строку s = '0' + n1*'1' + n2*'2' + n3*'3' # начинаем цикл перебора и замены while ('01' in s) or ('02' in s) or ('03' in s): s = s.replace('01','30',1) s = s.replace('02','3103',1) s = s.replace('03','1201',1) # выведем результат, удовлетворяющий условию задачи (с - количество "3" в исходной строке) if s.count('1') == 31 and s.count('2') == 24 and s.count('3') == 46: print(n1) exit() |
||
| Pascal(2 способ, традиционный): |
Укажите минимальную возможную длину входной строки
12_11:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
заменить (v, w) нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для Редактора:
ПОКА нашлось (555) ИЛИ нашлось (888) заменить (555, 8) заменить (888, 55) КОНЕЦ ПОКА
Известно, что начальная строка состоит более чем из 300 цифр 5 и не содержит других символов. В ходе работы алгоритма получилась строка, содержащая одну цифру 5 и одну цифру 8. Укажите минимальную возможную длину входной строки.
Ответ: 305
Показать решение:
-
✎ Решение 1. Программное:
PascalABC.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
begin for var i := 301 to 1000 do begin var s := '5' * i; while ('555' in s) or ('888' in s) do begin s := s.Replace('555', '8', 1); s := s.Replace('888', '55', 1); end; if (s.countOf('5') = 1) and (s.countOf('8') = 1) then begin print(i); break; end end; end. |
Pascal (традиционный):
|
||
| Python: | С++: |
Какое наибольшее / наименьшее количество … могло быть в исходной строке?
12_12:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
заменить (v, w) нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
К исходной строке, содержащей не более 100 троек и не содержащей других символов, применили приведённую ниже программу:
НАЧАЛО ПОКА нашлось (333) заменить (333, 4) заменить (4444, 3) КОНЕЦ ПОКА КОНЕЦ
В результате получилась строка 43.
Какое наибольшее количество троек могло быть в исходной строке?
Ответ: 92
Показать решение:
-
✎ Решение 1. Программное:
PascalABC.net (1 способ):
Вывод: 4 15 26 37 48 59 70 81 92
|
Python:
for i in range(1,100): s="3"*i while "333" in s: s=s.replace("333","4",1) s=s.replace("4444","3",1) if s=="43": print(i) Вывод: 4 15 26 37 48 59 70 81 92
|
||
Pascal(2 способ, традиционный):
|
Решение заданий прошлых лет (до 2021)
Исполнитель Робот
12_1:
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает 4 команды-приказа и 4 команды проверки условия.
Команды-приказы:
вверх вниз влево вправо
Другие четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Сколько клеток приведенного лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО ПОКА < снизу свободно ИЛИ справа свободно > ЕСЛИ < справа свободно > ТО вправо КОНЕЦ ЕСЛИ ПОКА < снизу свободно > вниз КОНЕЦ ПОКА КОНЕЦ ПОКА КОНЕЦ

Ответ: 21
✍ Показать решение:
- Рассмотрим тело внешнего цикла и операторы, которые в нем находятся:
- 1. В цикле выполняется проверка ЕСЛИ справа свободно ТО вправо: что означает движение на один шаг вправо (если это возможно)
- 2. Затем располагается цикл с условием пока снизу свободно вниз: что означает движение до конца вниз (пока это возможно)
- После чего внешний цикл повторяется.
- Таким образом, отметим «тупиковые» клетки, т.е. те, которые не позволят двигаться роботу к цели:
A5, A6, B1, B2, B6, C1, C2, D1, D2, D3, D4, D5, E3, E4, E5
36 - 15 = 21
12_2:
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА < справа свободно ИЛИ снизу свободно >
ПОКА < снизу свободно >
вниз
КОНЕЦ ПОКА
ПОКА < справа свободно >
вправо
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
Ответ: 19
✍ Показать решение:
Результат: 19
📹 Видео
Исполнитель Чертежник
12 задание. Демоверсия ЕГЭ 2018 информатика:
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x,y) в точку с координатами (x + a, y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (4, 6)
ПОВТОРИ … РАЗ
сместиться на (…, …)
сместиться на (4, -6)
КОНЕЦ ПОВТОРИ
сместиться на (-28, -22)
КОНЕЦ
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку.
Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Подобные задания для тренировки
Ответ: 8
✍ Показать решение:
Результат: 8
📹 Видео