Найдите все значения a, при каждом из которых система уравнений
имеет ровно три различных решения.
Спрятать решение
Решение.
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим три случая.
1) Если то получаем уравнение
Полученное уравнение задаёт прямую
2) Если то координаты любой точки прямой
удовлетворяют уравнению.
3) Если то получаем уравнение
Полученное уравнение задаёт окружность с центром в точке и радиусом 1.
Таким образом, в первом случае мы получаем луч r с началом в точке во втором — прямую l, задаваемую уравнением
в третьем — дугу
окружности
с концами в точках A и
(см. рис.).
Рассмотрим второе уравнение системы. При каждом значении a оно задаёт прямую m, которая проходит через точку (−2; 0) и угловой коэффициент которой равен a.
Прямые m проходят через точки B и A при и
соответственно.
При и
прямые m касаются дуги
Таким образом, прямая m пересекает прямую l при любом значении a, пересекает луч r при имеет одну общую точку с дугой
при
и
имеет две общие точки с дугой
при
и
Число решений исходной системы равно числу точек пересечения прямой l, луча r и дуги ω с прямой m. Таким образом, исходная система имеет ровно три решения при
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения полученно множество значений a, отличающееся от искомого только включением точки |
3 |
| C помощью верного рассуждения получен промежуток |
2 |
| Задача верно сведена к исследованию взаимного расположения дуги окружности, луча и прямых (аналитически или графически)
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Источник: Задания 18 (С6) ЕГЭ 2016
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задание
22
#2580
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых система [begin{cases} dfrac{(y^2-xy+3x-y-6)sqrt{x+2}}{sqrt{6-x}}=0\[2ex]
x+y-a=0end{cases}]
имеет два различных решения.
(ЕГЭ 2015, досрочная волна)
Преобразуем скобку в числителе дроби: [y^2-xy+3x-y-6=0
quadLeftrightarrowquad y^2-(x+1)y+3x-6=0] Дискриминант равен (D=(x-5)^2quadRightarrow) [y_1=dfrac{x+1+x-5}2=x-2quadtext{и}quad
y_2=dfrac{x+1-x+5}2=3.] Таким образом, всю систему можно записать в виде: [begin{cases} left[begin{gathered}begin{aligned}
&y^2-(x+1)y+3x-6=0\
&x+2=0end{aligned}end{gathered} right.\
6-x>0\
x+2geqslant 0\
y=-x+aend{cases} quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} &y=x-2\
&y=3\
&x=-2end{aligned}end{gathered} right.\
-2leqslant x<6\
y=-x+aend{cases}]
Найдем значения параметра, при каждом из которых прямая (y=-x+a) имеет две точки пересечения с графиком системы (begin{cases}
left[begin{gathered}begin{aligned} &y=x-2\
&y=3\
&x=-2end{aligned}end{gathered} right.\
-2leqslant x<6end{cases})
Рассмотрим рисунок:
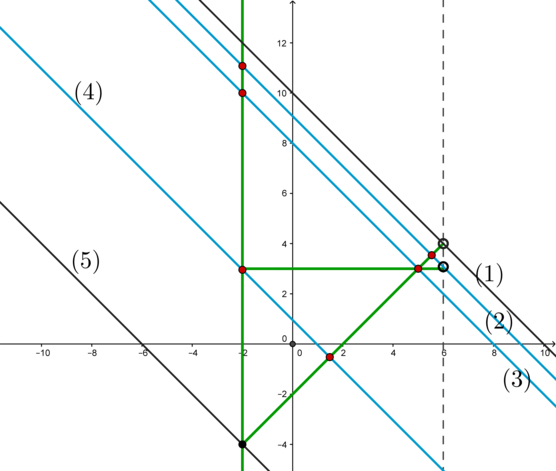
Зеленым цветом изображен график системы, синим и черным – возможные положения прямой (y=-x+a).
1) Заметим, что если прямая (y=-x+a) находится в положении (1) (проходит через точку ((6;4)) пересечения (y=x-2) и (x=6)) и выше, то она имеет только одну точку пересечения с графиком системы.
Между положениями (1) и (2) и в положении (2) (проходит через точку ((6;3)) пересечения (y=3) и (x=6)) прямая (y=-x+a) имеет две точки пересечения с графиком системы. Найдем соответствующие значения параметра.
Положение (1): (a=10);
положение (2): (a=9).
Следовательно, при (ain[9;10)) имеем две точки пересечения.
2) Между положениями (2) и (3) – три точки пересечения, а вот в положении (3) (проходит через точку ((5;3)) пересечения (y=3) и (y=x-2)) – две точки.
Положение (3): (a=8).
3) Между положениями (3) и (4) – три точки пересечения, а вот в положении (4) (проходит через точку ((-2;3)) пересечения (y=3) и (x=-2)) – две точки.
Положение (4): (a=1).
4) Между положениями (4) и (5) – две точки пересечения.
Положение (5) – прямая (y=-x+a) проходит через точку ((-2;-4)) пересечения (x=-2) и (y=x-2), следовательно, (a=-6).
Следовательно, при (ain (-6;1)) имеем две точки пересечения.
Собрав все подходящие значения параметра, получим: (ain
(-6;1]cup{8}cup[9;10)).
Ответ:
(ain (-6;1]cup{8}cup[9;10))
Задание
23
#2574
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых неравенство [|3sin x+a^2-22|+|7sin x+a+12|leqslant 11sin
x+|a^2+a-20|+11]
выполнено для всех значений (x).
(ЕГЭ 2014, вторая волна, резерв)
Сделаем замену: (sin x+1=t), следовательно, (tin [0;2]). Тогда неравенство примет вид: [|3t+a^2-25|+|7t+a+5|leqslant
11t+|a^2+a-20|] Заметим, что при раскрытии модулей в левой части (на соответствующем промежутке) коэффициент перед (t) (в левой части) будет равен либо (7+3=10), либо (7-3=4), либо (3-7=-4), либо (-3-7=-10). В любом случае при переносе данного слагаемого в правую часть и приведении подобных слагаемых коэффициент перед (t) (в правой части) будет положительным.
Например, если модули раскроются оба положительными (то есть (3t>-a^2+25, 7t>-a-5)), то неравенство для таких (t) примет вид: [3t+a^2-25+7t+a+5leqslant 11t+|a^2+a-20|quadLeftrightarrowquad
0leqslant t+|a^2+a-20|-a^2-a+20quadLeftrightarrowquad
t+|a^2+a-20|-a^2-a+20geqslant0] Следовательно, справа получается возрастающая линейная функция.
Таким образом, можно сделать вывод, что как бы ни раскрылись модули, функция (y(t)=11t+|a^2+a-20|-|3t+a^2-25|-|7t+a+5|) всегда будет монотонно возрастающей.
Поэтому если рассмотреть неравенство в виде [y(t)=11t+|a^2+a-20|-|3t+a^2-25|-|7t+a+5|geqslant 0,] то для того, чтобы неравенство при всех (tin[0;2]) выполнялось, достаточно, чтобы график возрастающей функции (y(t)) был выше оси (Ox). Следовательно, значение (y(0)) (в левой точке отрезка ([0;2])) должно быть неотрицательным:
[11cdot 0+|a^2+a-20|-|3cdot 0+a^2-25|-|7cdot 0+a+5|geqslant 0
quadLeftrightarrowquad |a^2+a-20|geqslant|a^2-25|+|a+5|] Заметим, что (a^2-25+a+5=a^2+a-20). Следовательно, данное неравенство имеет вид: (|A+B|geqslant |A|+|B|). Как известно, при всех (A) и (B) выполняется неравенство: (|A+B|leqslant |A|+|B|). Следовательно, наше неравенство выполняется тогда и только тогда, когда [|A+B|=|A|+|B|] Для того, чтобы модуль суммы был равен сумме модулей двух чисел (A) и (B), хотя бы одно из них должно быть равно нулю либо они должны быть одного знака, следовательно, данное равенство равносильно [ABgeqslant 0quadRightarrowquad (a^2-25)(a+5)geqslant 0quadRightarrowquad
(a+5)^2(a-5)geqslant 0quadRightarrowquad ain
{-5}cup[5;+infty).]
Ответ:
(ain {-5}cup[5;+infty))
Задание
24
#2575
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых уравнение [(mathrm{tg},x+6)^2-(a^2+2a+8)(mathrm{tg},x+6)+a^2(2a+8)=0]
имеет ровно два различных решения на отрезке (left[0;dfrac{3pi}2right]).
(ЕГЭ 2014, вторая волна)
Заметим, что (mathrm{tg},x) – периодическая функция с периодом (pi). Таким образом, если данное уравнение будет иметь решение на (left[0;frac{pi}2right)), то оно также будет иметь еще одно решение на (left[pi;frac{3pi}2right)) (в точках (frac{pi}2,
frac{3pi}2) тангенс не определен). А вот решения из промежутка (left(frac{pi}2;piright)) не дублируются на отрезке (left[0;dfrac{3pi}2right]).
Таким образом, данное уравнение будет иметь два решения на отрезке (left[0;dfrac{3pi}2right]) в одном из двух случаев:
1) Если оно будет иметь ровно одно, причем неотрицательное, решение относительно (mathrm{tg},x).
2) Если оно будет иметь ровно два различных, причем отрицательных, решения относительно (mathrm{tg},x).
Рассмотрим первый случай.
Введем обозначение (mathrm{tg},x+6=t). Тогда (tgeqslant 6). Получим уравнение: [t^2-(a^2+2a+8)t+a^2(2a+8)=0]Заметим, что по теореме Виета корнями данного уравнения будут: [t_1=2a+8quadtext{и}quad t_2=a^2]Для того, чтобы уравнение имело ровно один корень, причем (tgeqslant 6), нужно:[begin{cases} t_1=t_2\t_1geqslant 6end{cases}
quadRightarrowquad a=4.]
Рассмотрим второй случай.
Т.к. в этом случае (mathrm{tg},x<0quadRightarrowquad t<6).
Также остается: [t_1=2a+8quadtext{и}quad t_2=a^2] Для того, чтобы уравнение имело два корня, причем оба были меньше (6), нужно:[begin{cases} t_1ne
t_2\t_1<6\t_2<6end{cases}quadRightarrowquad
begin{cases}-sqrt6<a<-1\ane -2end{cases}]
Таким образом, окончательный ответ в задаче: [ain
(-sqrt6;-2)cup(-2;-1)cup{4}.]
Ответ:
(ain(-sqrt6;-2)cup(-2;-1)cup{4})
Задание
25
#2576
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых уравнение [left(x+dfrac1{x-a}right)^2-(a+9)left(x+dfrac1{x-a}right)+2a(9-a)=0]
будет иметь четыре различных решения.
(ЕГЭ 2014, резерв)
1) Сделаем замену: (x+frac1{x-a}=t). Полученное уравнение [t^2-(a+9)t+2a(9-a)=0] по теореме Виета имеет два (может быть, совпадающих) корня [t_1=9-aquadtext{и}quad t_2=2a.] Заметим, что для того, чтобы исходное уравнение имело четыре решения, необходимо, чтобы полученное уравнение относительно (t) имело два различных решения. Следовательно, [9-ane
2aquadLeftrightarrowquad ane 3]
2) Сделаем обратную замену: [left[begin{gathered}begin{aligned}
&x+dfrac1{x-a}=2a\[2ex]
&x+dfrac1{x-a}=9-a end{aligned}end{gathered}right.
quadLeftrightarrowquadbegin{cases}left[begin{gathered}begin{aligned}
&x^2-9x-a^2+9a+1=0\
&x^2-3ax+2a^2+1=0
end{aligned}end{gathered}right.\xne aend{cases}]
Следовательно, каждое из двух полученных квадратных уравнений должно иметь два различных корня, не равные (a), причем все четыре этих корня должны быть различны.
а) Значит, во-первых, у уравнений должны быть положительные дискриминанты: [begin{cases} D_1=4a^2-36a+77>0\
D_2=a^2-4>0end{cases} quadLeftrightarrowquad ain
(-infty;-2)cupleft(2;frac72right)cupleft(frac{11}2;+inftyright)]
б) Во-вторых, (x=a) не должно являться корнем ни одного из двух уравнений, то есть [begin{cases} a^2-9a-a^2+9a+1ne 0\
a^2-3a^2+2a^2+1ne 0end{cases} quadLeftrightarrowquad ain
mathbb{R}]
в) В-третьих, ни один корень одного уравнения не должен совпадать ни с одним корнем второго уравнения. Найдем значения (a), при которых уравнения имеют одинаковый корень (x_0): [x_0^2-9x_0-a^2+9a+1=x_0^2-3ax_0+2a^2+1quadLeftrightarrowquad
(a-3)(x_0-a)=0] Таким образом, либо (a) должно быть равно (3) (но это значение параметра мы исключили в 1-ом пункте решения), либо этот общий корень должен быть равен (a) (это мы также проверили в б)).
Следовательно, учитывая (ane 3), получаем окончательный ответ [ain
(-infty;-2)cup(2;3)cupleft(3;frac72right)cup
left(frac{11}2;+inftyright)]
Ответ:
(ain
(-infty;-2)cup(2;3)cupleft(3;frac72right)cupleft(frac{11}2;+inftyright))
Задание
26
#2573
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых уравнение [(|x+2|+|x-a|)^2-5cdot (|x+2|+|x-a|)+3a(5-3a)=0]
имеет ровно два различных решения.
(ЕГЭ 2014, основная волна)
1) Сделаем замену (t=|x+2|+|x-a|). Тогда уравнение примет вид [t^2-5t+3a(5-3a)=0.] Получили квадратное уравнение. Для того, чтобы изначальное уравнение относительно (x) имело решения, полученное уравнение относительно (t) должно иметь решения, то есть его дискриминант должен быть неотрицательным. Найдем дискриминант: [D=25-60a+36a^2=(6a-5)^2geqslant 0.] Таким образом, дискриминант для любого (a) будет неотрицательным. Имеем корни: [t_1=dfrac{5+6a-5}2=3aqquad text{и}qquad
t_2=dfrac{5-6a+5}2=5-3a.]
2) Таким образом, исходное уравнение равносильно совокупности: [left[begin{gathered}begin{aligned} &|x+2|+|x-a|=3a\&|x+2|+|x-a|=5-3a
end{aligned}end{gathered} right.] Оба уравнения в данной совокупности имеют вид: [|x+2|+|x-a|=t,]где (t) – некоторое выражение, зависящее от (a). Исследуем такое уравнение.
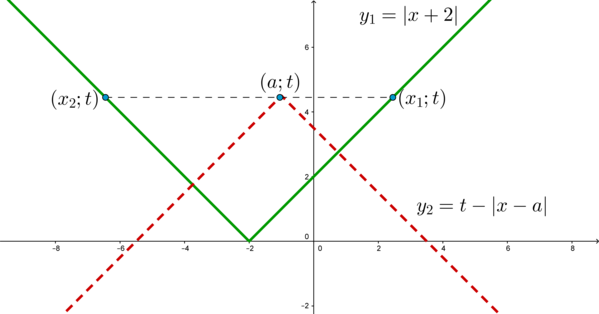
Заметим, что т.к. модуль всегда неотрицателен, то и сумма двух модулей всегда неотрицательна, то есть слева стоит неотрицательное выражение. Значит, для того, чтобы данное уравнение имело решения, необходимо, чтобы (tgeqslant 0). Рассмотрим уравнение в виде: [|x+2|=t-|x-a|] Пусть (y_1=|x+2|, y_2=t-|x-a|). Тогда график (y_1) представляет собой угол с ветвями вверх, вершина которого находится в точке ((-2;0)), а график (y_2) – угол с ветвями вниз, вершина которого находится в точке ((a;t)) (помним, что (tgeqslant 0)).
Тогда уравнение будет иметь два решения (то есть две точки пересечения графиков (y_1) и (y_2)), если вершина угла (y_2) находится внутри угла (y_2). Одно решение, если вершины углов совпадут (тогда (a=-2, t=0)). Бесконечное множество решений (отрезок), если вершина угла (y_2) попадет на одну из ветвей угла (y_1). Не будет иметь решений, если вершина угла (y_2) будет находиться снаружи угла (y_1).
Рассмотрим интересующий нас случай, когда уравнение имеет два решения. Тогда (a) должно находиться между числами (x_2) и (x_1).
Правая ветвь угла (y_1) задается уравнением (y=x+2), следовательно, (t=x_1+2quad Rightarrow quad x_1=t-2).
Левая ветвь задается уравнением (y=-x-2), следовательно, (t=-x_2-2quadRightarrowquad x_2=-t-2).
Таким образом, для того, чтобы уравнение имело два решения, необходимо и достаточно:[begin{cases} -t-2<a<t-2\tgeqslant
0end{cases}]
3) Заметим, что в нашем случае уравнение не может иметь одно решение, т.к. одновременное выполнение (a=-2) и (t=0) при (t=3a) или (t=5-3a) невозможно.
Следовательно, вся совокупность из двух уравнений будет иметь два решения тогда и только тогда, когда первое имеет два решения, а второе – ни одного, или наоборот.
4) Рассмотрим первое уравнение. [|x+2|=3a-|x-a|] Оно имеет два решения, когда:[begin{cases}
-3a-2<a<3a-2\3ageqslant 0end{cases} quadRightarrowquad a>1] Тогда оно не имеет решений, когда (aleqslant 1).
Рассмотрим второе уравнение. [|x+2|=5-3a-|x-a|] Оно имеет два решения, когда:[begin{cases}
-5+3a-2<a<5-3a-2\5-3ageqslant 0end{cases}quadRightarrowquad
a<dfrac34] Тогда оно не имеет решений, когда (ageqslant
frac34).
5) Таким образом, нужно: [left[begin{gathered}begin{aligned}
&begin{cases} a>1\ageqslantfrac34end{cases}\
&begin{cases}
aleqslant 1\a<frac34end{cases}
end{aligned}end{gathered}right. quadRightarrowquad
ainleft(-infty;frac34right)cup(1;+infty).]
Ответ:
(left(-infty;frac34right)cup(1;+infty))
Задание
27
#2577
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых уравнение [left(log_8(x+a)-log_8(x-a)right)^2-12aleft(log_8(x+a)-log_8(x-a)right)
+35a^2-6a-9=0]
имеет два различных решения.
(ЕГЭ 2014, основная волна)
1) Сделаем замену: (t=log_8(x+a)-log_8(x-a)), тогда уравнение примет вид [t^2-12at+35a^2-6a-9=0] Дискриминант данного уравнения равен [D=4(a+3)^2geqslant 0]Следовательно, уравнение всегда имеет два (быть может, совпадающих) корня [t_1=dfrac{12a+2a+6}2=7a+3qquadtext{и}qquad t_2=dfrac{12a-2a-6}2=5a-3.]
2) Запишем ответ для (x) в общем виде. Пусть (b) – корень уравнения (t^2-12at+35a^2-6a-9=0). Тогда, сделав обратную замену, получаем [log_8(x+a)-log_8(x-a)=bquadLeftrightarrowquad begin{cases}
log_8dfrac{x+a}{x-a}=b\
x>a\
x>-aend{cases}quadLeftrightarrowquad begin{cases}
left(8^b-1right)x=aleft(8^b+1right)\
x>|a| end{cases}]
При (b=0) коэффициент (8^b-1) перед (x) равен нулю, следовательно, уравнение системы примет вид: (0=2a). Данное уравнение при (a=0) будет иметь бесконечно много решений, при (ane 0) не будет иметь решений. Следовательно, сама система в каждом случае (после пересечения решения уравнения с ОДЗ (x>|a|)) будет иметь либо бесконечное множество решений, либо не иметь решений.
Т.к. случай с бесконечным множеством решений нам не подходит (нам нужно два решения), то (a) точно не равно нулю.
Таким образом, мы видим, что при каждом фиксированном (b) мы получаем либо одно решение для (x) (если (bne 0)): [x=acdot dfrac{8^b+1}{8^b-1},] либо ни одного решения для (x) (если (b=0, ane 0)).
Отсюда можно сделать вывод, что для того, чтобы исходное уравнение имело два решения, нужно, чтобы (t_1ne t_2 quad text{и}quad
t_1ne 0,t_2ne 0):[7a+3ne 5a-3, 7a+3ne 0, 5a-3ne 0
quadLeftrightarrowquad ane -3; -dfrac37; dfrac35,] а также, чтобы полученные корни для (x) удовлетворяли ОДЗ (x>|a|).
3) Найдем в общем виде условия, при которых корень (x=acdotdfrac{8^b+1}{8^b-1}) удовлетворяет ОДЗ (x>|a|). [acdot dfrac{8^b+1}{8^b-1}>|a| quadRightarrowquad left[begin{gathered}
begin{aligned} &begin{cases}a> 0\ dfrac{8^b+1}{8^b-1}>1end{cases}\
&begin{cases} a<0\ dfrac{8^b+1}{8^b-1}<-1end{cases}
end{aligned} end{gathered} right. quadLeftrightarrowquad
left[begin{gathered}
begin{aligned} &begin{cases}a> 0\ b>0end{cases}\
&begin{cases} a<0\ b<0end{cases}
end{aligned} end{gathered} right.]
4) Подставим наши корни (t_1=7a+3) и (t_2=5a-3) вместо (b):
[left[begin{gathered}
begin{aligned} &begin{cases}a> 0\ 7a+3>0end{cases}\
&begin{cases} a<0\ 7a+3<0end{cases}
end{aligned} end{gathered} right.quadLeftrightarrowquad
ain left(-infty;-frac37right)cup(0;+infty)] и [left[begin{gathered}
begin{aligned} &begin{cases}a> 0\ 5a-3>0end{cases}\
&begin{cases} a<0\ 5a-3<0end{cases}
end{aligned} end{gathered} right.quadLeftrightarrowquad
ain (-infty;0)cupleft(frac35;+inftyright).]
Пересекая данные решения между собой и с (ane -3; -frac37;
frac35) (найденные во 2-ом пункте), получим окончательный ответ [ain (-infty;-3)cupleft(-3;-frac37right)cupleft(frac35;+inftyright).]
Ответ:
(ain
(-infty;-3)cupleft(-3;-frac37right)cupleft(frac35;+inftyright))
Задание
28
#2966
Уровень задания: Равен ЕГЭ
Найдите все значения (a), для каждого из которых существует хотя бы одна пара чисел (x) и (y), удовлетворяющих неравенству [4|x+3|+3|x-a|leqslant sqrt{16-y^2}+2]
(ЕГЭ 2013, основная волна)
Рассмотрим две функции (f(x)=4|x+3|+3|x-a|) и (h(y)=sqrt{16-y^2}+2).
Заметим, что при (x<-3) модуль (|x+3|=-x-3), а при (x>-3) модуль (|x+3|=x+3). Следовательно, вне зависимости от того, как раскроется модуль (|x-a|), при (x<-3) коэффициент перед (x) у функции (f(x)) будет отрицательным (а именно -7 или -1), а при (x>-3) он будет положительным (а именно 1 или 7). Следовательно, (f(x)) имеет минимум в точке (x=-3). Это значит, что (f(x)geqslant f(-3)) при всех (x).
Так как (y^2geqslant 0) при всех (y) и по ОДЗ (16-y^2geqslant 0), то (sqrt{0}leqslant sqrt{16-y^2}leqslant sqrt{16}), значит, функция (h(y)in [2;6]) при всех (y).
Таким образом, если (f(-3)>6), то неравенство (f(x)leqslant h(y)) не имеет решений, так как левая часть больше (6), а правая – меньше или равна (6).
Следовательно, (f(-3)leqslant 6). При этом нам подходит как минимум одна пара чисел: (x=-3) и (y=0) (Проверьте!).
Так как (f(-3)=3|-3-a|=3|a+3|), то получаем: [3|a+3|leqslant 6quadLeftrightarrowquad ain [-5;-1].]
Ответ:
([-5;-1])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
На чтение 1 мин Просмотров 18 Опубликовано 5 марта, 2023
Тригонометрические уравнения решу ЕГЭ 2022 профиль с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Задание №1 ЕГЭ 2022 профильный уровень тригонометрические уравнения 6 задач решу ЕГЭ с ответами и решением для подготовки, решаем примеры
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%82%d1%80%d0%b8%d0%b3%d0%be%d0%bd%d0%be%d0%bc%d0%b5%d1%82%d1%80%d0%b8%d1%87%d0%b5%d1%81%d0%ba%d0%b8%d0%b5-%d1%83%d1%80%d0%b0%d0%b2%d0%bd%d0%b5%d0%bd%d0%b8%d1%8f-%d1%80%d0%b5%d1%88%d1%83-%d0%b5/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
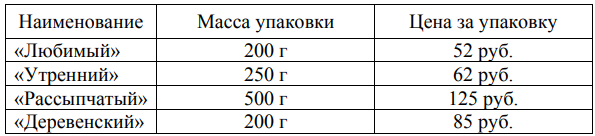
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
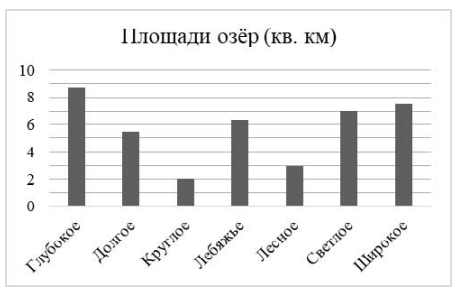
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
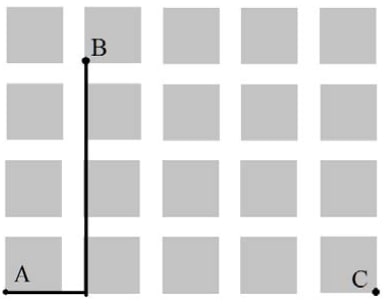
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Натуральное рациональное
шестизначное
число 514740
является составным.
Произведение всех цифр числа: 0.
Число имеет следующие делители: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 23, 30, 46, 60, 69, 92, 115, 138, 230, 276, 345, 373, 460, 690, 746, 1119, 1380, 1492, 1865, 2238, 3730, 4476, 5595, 7460, 8579, 11190, 17158, 22380, 25737, 34316, 42895, 51474, 85790, 102948, 128685, 171580, 257370, 514740.
Их сумма: 1507968.
0.0000019427283677196254 является обратным числом к 514740.
Число 514740 представляется произведением простых чисел: 2 * 2 * 3 * 5 * 23 * 373.
Перевод числа в другие системы счисления:
двоичная система счисления: 1111101101010110100, троичная система счисления: 222011002110, восьмеричная система счисления: 1755264, шестнадцатеричная система счисления: 7DAB4.
502 килобайта 692 байта — столько информации находится в числе байт 514740.
В виде кода азбуки Морзе: ….. .—- ….- —… ….- ——
Число — не число Фибоначчи.
Синус числа 514740: 0.5068, косинус числа 514740: -0.8620, тангенс числа 514740: -0.5880.
Натуральный логарифм числа равен 13.1514.
Логарифм десятичный числа равен 5.7116.
717.4538 это корень квадратный из числа, 80.1425 — кубический.
Возведение числа в квадрат: 2.6496e+11.
Число 514740 в секундах это 5 дней 22 часа 59 минут ноль секунд.
Цифра 3 — это нумерологическое значение этого числа.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами