Решу егэ 517468 - Помощь в подготовке к экзаменам и поступлению

Решите неравенство:

Спрятать решение

Решение.

Пусть тогда:

Вернёмся к исходной переменной:

Ответ:

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Источник: Задания 15 (С3) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).

Источник

Свойства натурального числа 517468, 0x07E55C, 0x7E55C:

Рейтинг 0 из 10,
оценок: 0.

Системы счисления, перевод в систему счисления

Десятичное число 517468

517468 в шестнадцатеричной системе счисления

7E55C
517468 в двоичной системе счисления

1111110010101011100
517468 в восьмеричной системе счисления

1762534

Шестнадцатеричное число 7E55C

7E55C в десятичной системе

517468
7E55C в двоичной системе

1111110010101011100
7E55C в восьмеричной системе

1762534

Двоичное число 1111110010101011100

1111110010101011100 в десятичной системе

517468
1111110010101011100 в шестнадцатеричной системе

7E55C
1111110010101011100 в восьмеричной системе

1762534

Восьмеричное число 1762534

1762534 в десятичной системе

517468
1762534 в шестнадцатеричной системе

7E55C
1762534 в двоичной системе

1111110010101011100

Основные арифметические и алгебраические свойства

Число 517468 на русском языке, number in Russian, число 517468 прописью:

пятьсот семнадцать тысяч четыреста шестьдесят восемь
Четность

Четное число 517468
Разложение на множители, делители числа 517468

2, 2, 7, 18481, 1
Простое или составное число

Составное число 517468
Числа делящиеся на целое число 517468

1034936, 1552404, 2069872, 2587340, 3104808, 3622276, 4139744, 4657212
Число 517468 умноженное на число два

1034936
517468 деленное на число 2

258734
Список 8-ми простых чисел перед числом

517459, 517457, 517417, 517411, 517403, 517399, 517393, 517381
Сумма десятичных цифр

31
Количество цифр

6
Десятичный логарифм 517468

5.7138834983741
Натуральный логарифм 517468

13.156702966461
Это число Фибоначчи?

Нет
Число на 1 больше числа 517468,
следующее число

число 517469
Число на 1 меньше числа 517468,
предыдущее число

517467

Степени числа, корни

517468 во второй степени (в квадрате)
(функция x в степени 2 — x²)

267773131024
В третьей степени (в кубе, 517468 в степени 3, x³) равно

138564026564727232
Корень квадратный из 517468

719.35248661557
Корень кубический из числа 517468 =

80.283783810712

Тригонометрические функции, тригонометрия

Синус, sin 517468 градусов, sin 517468°

0.5299192642
Косинус, cos 517468 градусов, cos 517468°

-0.8480480962
Тангенс, tg 517468 градусов, tg 517468°

-0.6248693519
Синус, sin 517468 радиан

-0.53631411892314
Косинус, cos 517468 радиан

-0.8440184629756
Тангенс, tg 517468 радиан равно

0.63542936849077
517468 градусов, 517468° =

9031.52037371 радиан
517468 радиан =

29648732.433076 градуса, 29648732.433076°

Контрольные суммы, хэши, криптография

MD-5 хэш(517468)

d3e4029427aa766ffa42fd454b28d3b4
CRC-32, CRC32(517468)

2528379444
SHA-256 hash, SHA256(517468)

6512d6082378667055c2e07b33b524fc058b67792e8ed5536ce11ab66b37833b
SHA1, SHA-1(517468)

6c3eac4f28eff44d7afb71ef320fe9dd1e2d4ab3
ГОСТ Р 34.11, GOST R 34.11-94, GOST(517468)

4b643fa40d1f39a0c9fb85ad3b7ec77ee64a6db60d92e2c9bd2fe2423624e6de
Base64

NTE3NDY4

Языки программирования

C++, CPP, C значение 517468

0x07E55C, 0x7E55C
Delphi, Pascal значение числа 517468

$07E55C

Дата и время

Конвертация UNIX timestamp 517468 в дату и время

UTC

вторник, 6 января 1970 г., 23:44:28 GMT

в Москве, Россия

среда, 7 января 1970 г., 2:44:28 Московское стандартное время

в Лондоне, Великобритания

среда, 7 января 1970 г., 0:44:28 GMT+01:00

в Нью-Йорке, США

вторник, 6 января 1970 г., 18:44:28 Восточно-американское стандартное время

Интернет

Конвертация в IPv4 адрес Интернет

0.7.229.92
517468 в Википедии:

517468

Другие свойства числа

Короткая ссылка на эту страницу, DEC

https://bikubik.com/ru/517468
Короткая ссылка на эту страницу, HEX

https://bikubik.com/ru/x7E55C
Номер телефона

51-74-68

Цвет по числу 517468, цветовая гамма

html RGB цвет 517468, 16-ричное значение

#07E55C — (7, 229, 92)
HTML CSS код цвета #07E55C

.color-mn { color: #07E55C; }
.color-bg { background-color: #07E55C; }

Цвет для данного числа 517468

Здесь вы можете изменить составляющую цвета для данного числа 517468 или цвета 07E55C:

Источник

Целое натуральное

число 517468
является составным числом.

31 — сумма цифр числа.
У числа 517468 12 делителя.

Обратное число к 517468 – это 0.0000019324866465172726.

Число 517468 можно представить произведением: 2 * 2 * 7 * 18481.

Представления числа 517468:
двоичная система: 1111110010101011100, троичная: 222021211111, восьмеричная: 1762534, шестнадцатеричная: 7E55C.
Число байт 517468 – это 505 килобайтов 348 байтов .

Число 517468 азбукой Морзе: ….. .—- —… ….- -…. —..

Косинус: -0.8440, тангенс: 0.6354, синус: -0.5363.
Число 517468 имеет натуральный логарифм: 13.1567.
Десятичный логарифм числа 517468: 5.7139.
Если из числа извлечь квадратный корень, получится 719.3525, а если кубический — 80.2838
Квадрат числа: 2.6777e+11.

Число секунд 517468 можно представить как 5 дней 23 часа 44 минуты 28 секунд .
Нумерологическое значение числа 517468 – цифра 4.

Источник

В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.

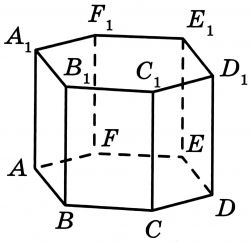
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.

В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.

Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.

Найдите корень уравнения (left(dfrac19right)^{x+4}=729)

Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)

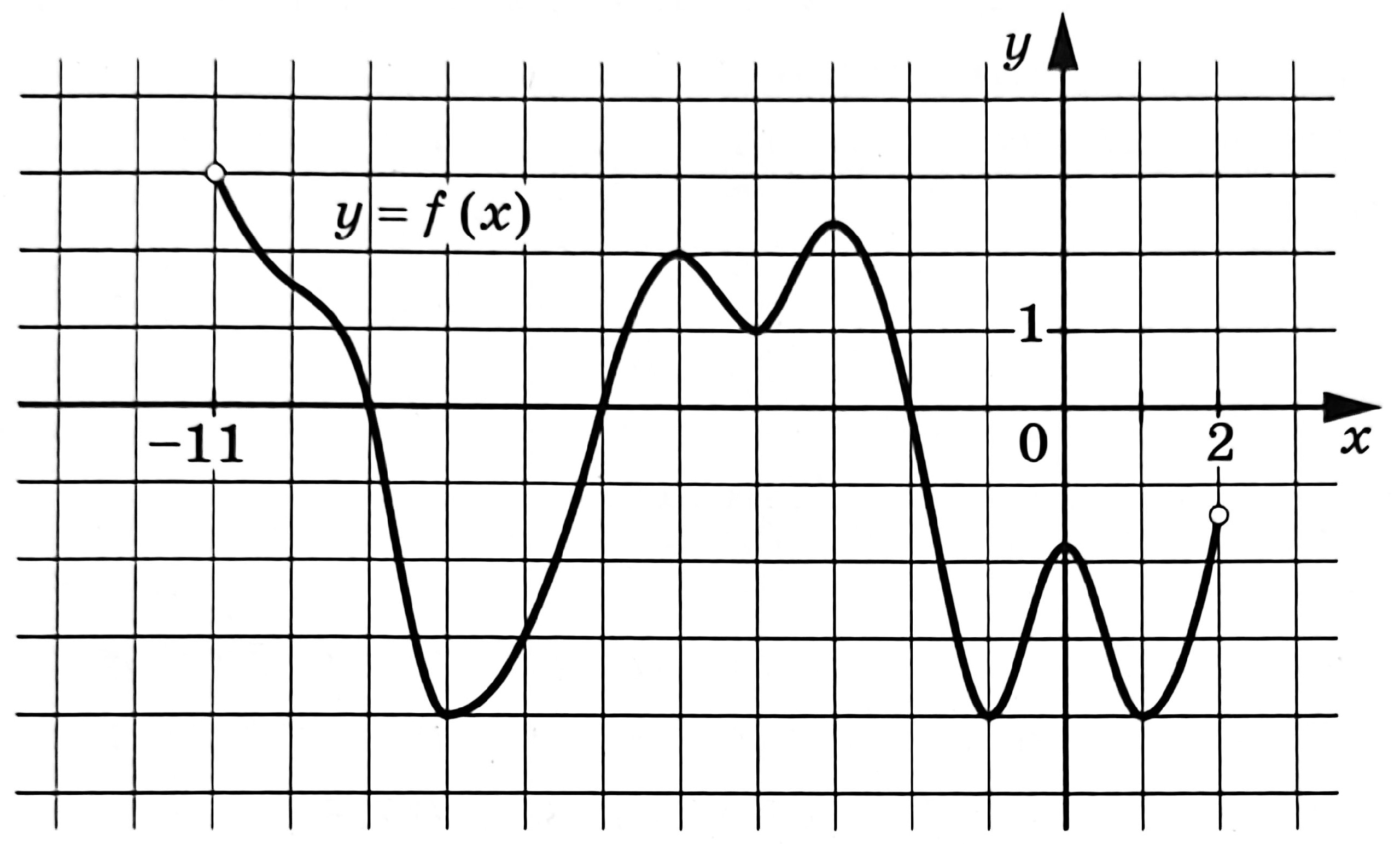
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.

Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

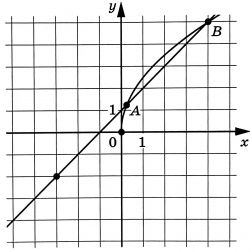
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.

Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])

а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])

Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.

Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)

15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.

Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.

Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.

Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?

Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Источник

508780 решу егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 14 № 508380

Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:

Приведем другое решение:

Как и в первом решении запишем неравенство в виде:

Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:

Задание 14 № 508380

—>

508780 решу егэ математика.

Ege. sdamgia. ru

07.03.2017 0:00:13

2017-03-07 00:00:13

Источники:

Https://ege. sdamgia. ru/problem? id=508380

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика

508780 решу егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 10 № 508781

Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?

Задание 10 № 508782

Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?

Задание 10 № 508783

Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508784

Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508785

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508786

Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508787

Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508788

Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508789

Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508790

Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508786

Задание 10 № 508781

Задание 10 508786.

Ege. sdamgia. ru

14.05.2019 20:28:53

2019-05-14 20:28:53

Источники:

Https://ege. sdamgia. ru/test? likes=508780

508780 решу егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 10 № 508780

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей

—>

Задание 10 № 508780

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Ege. sdamgia. ru

09.08.2017 16:57:34

2017-08-09 16:57:34

Источники:

Https://ege. sdamgia. ru/problem? id=508780

Источник