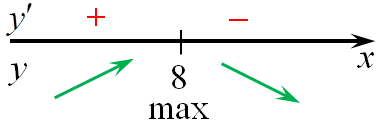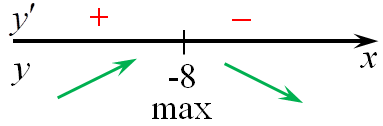Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 2,4 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением где
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 16 200 Дж.
Спрятать решение
Решение.
Задача сводится к решению уравнения :
Ответ: 9,6.
На чтение 1 мин Просмотров 20 Опубликовано 5 марта, 2023
Тригонометрические уравнения решу ЕГЭ 2022 профиль с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Задание №1 ЕГЭ 2022 профильный уровень тригонометрические уравнения 6 задач решу ЕГЭ с ответами и решением для подготовки, решаем примеры
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%82%d1%80%d0%b8%d0%b3%d0%be%d0%bd%d0%be%d0%bc%d0%b5%d1%82%d1%80%d0%b8%d1%87%d0%b5%d1%81%d0%ba%d0%b8%d0%b5-%d1%83%d1%80%d0%b0%d0%b2%d0%bd%d0%b5%d0%bd%d0%b8%d1%8f-%d1%80%d0%b5%d1%88%d1%83-%d0%b5/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Скрыть
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Скрыть
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Скрыть
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Скрыть
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Скрыть
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
Скрыть
Задание 10
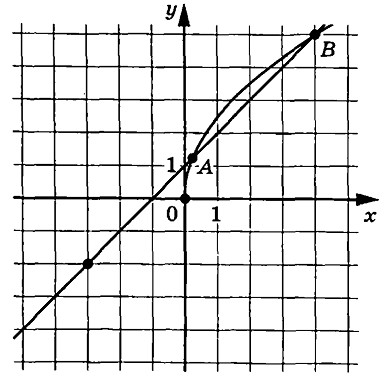
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Скрыть
ЕГЭ Профиль №11. Показательные функции
Скачать файл в формате pdf.
ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Если функция (fleft( x right)) определена и непрерывна на промежутке X и во всех внутренних точках этого промежутка имеет положительную производную (left( {f’left( x right) > 0} right)), то функция возрастает на X.
Если функция (fleft( x right)) определена и непрерывна на промежутке X и во всех внутренних точках этого промежутка имеет отрицательную производную (left( {f’left( x right) < 0} right)), то функция убывает на X.
Говорят, что функция (y = fleft( x right)) имеет максимум (минимум) в точке (x = a), если у этой точки существует окрестность, в которой (fleft( x right) < fleft( a right)quad left( {fleft( x right) > fleft( a right)} right)) для (x ne a).
Точки максимума и минимума объединяются общим термином – точки экстремума.
Правило исследования функции (y = fleft( x right)) на экстремум:
1. найти область определения функции;
2. найти (f’left( x right));
3. найти точки, в которых выполняется равенство (f’left( x right) = 0);
4. найти точки, в которых (f’left( x right)) не существует;
5. отметить на координатной прямой все точки в которых производная равна 0 или не существует и область определения функции (y = fleft( x right)); получатся промежутки области определения функции, на каждом из которых производная функции (y = fleft( x right)) сохраняет постоянный знак;
6. определить знак (f’left( x right)) на каждом из промежутков;
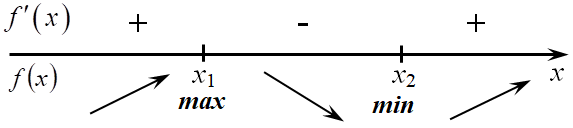
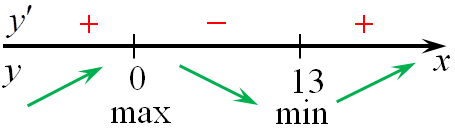
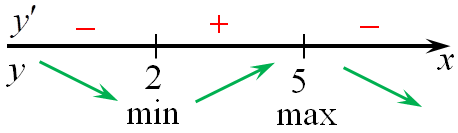
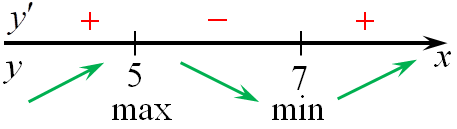
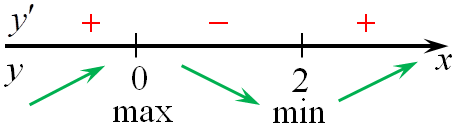
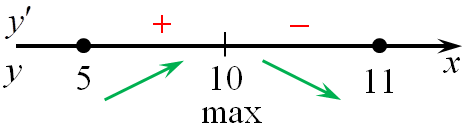
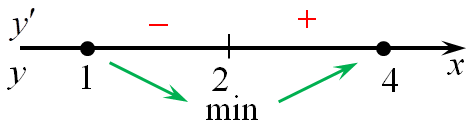
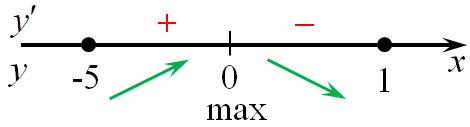
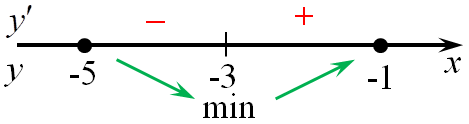
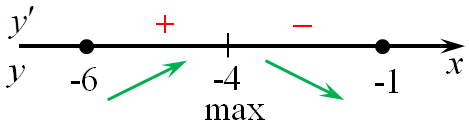
7. если при переходе через точку производная (f’left( x right)) меняет знак с «+» на «-», то эта точка является точкой максимума функции, а если с «-» на «+», то точкой минимума. На приведенном рисунке точка x1 является точкой максимума, а x2 точкой минимума.
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции (y = fleft( x right)) на отрезке :
1. найти (f’left( x right));
2. найти точки, в которых (f’left( x right) = 0) или (f’left( x right)) не существует, и отобрать из них те, что лежат внутри отрезка ;
3. вычислить значение функции (y = fleft( x right)) в точках, полученных в пункте 2, и на концах отрезка (в точках a и b) и далее выбрать из них наибольшее и наименьшее, которые будут соответственно наибольшим и наименьшим значениями функции (y = fleft( x right)) на отрезке . Эти значения обозначаются ({y_{наим}},;{y_{наиб}}).
ЕГЭ Профиль №11. Показательные функции
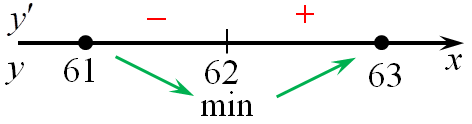
| Задача 1. Найдите наименьшее значение функции (y = left( {x — 63} right){e^{x — 62}}) на отрезке (left[ {61;63} right])
Ответ
ОТВЕТ: — 1. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {x — 63} right)^prime }{e^{x — 62}} + left( {x — 63} right){left( {{e^{x — 62}}} right)^prime } = {e^{x — 62}} + left( {x — 63} right){e^{x — 62}} = {e^{x — 62}}left( {1 + x — 63} right) = {e^{x — 62}}left( {x — 62} right).) Найдем нули производной: ({e^{x — 62}}left( {x — 62} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x — 62 = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = 62.) Определим знаки производной функции на отрезке (left[ {61;63} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ {61;63} right]) будет в точке (x = 62.) (yleft( {62} right) = left( {62 — 63} right){e^{62 — 62}} = — 1.) Ответ: – 1. |
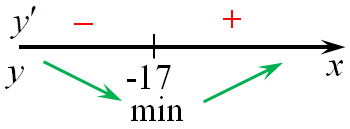
| Задача 2. Найдите точку минимума функции (y = left( {x + 16} right){e^{x — 16}})
Ответ
ОТВЕТ: — 17. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {x + 16} right)^prime }{e^{x — 16}} + left( {x + 16} right){left( {{e^{x — 16}}} right)^prime } = {e^{x — 16}} + left( {x + 16} right){e^{x — 16}} = )( {e^{x — 16}}left( {1 + x + 16} right) = {e^{x — 16}}left( {x + 17} right).) Найдем нули производной: ({e^{x — 16}}left( {x + 17} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x + 17 = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = — 17.) Определим знаки производной функции и её поведение: Следовательно, точка минимума (x = — 17.) Ответ: – 17. |
| Задача 3. Найдите точку максимума функции (y = left( {9 — x} right){e^{x + 9}})
Ответ
ОТВЕТ: 8. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {9 — x} right)^prime }{e^{x + 9}} + left( {9 — x} right){left( {{e^{x + 9}}} right)^prime } = — {e^{x + 9}} + left( {9 — x} right){e^{x + 9}} = {e^{x + 9}}left( { — 1 + 9 — x} right) = {e^{x + 9}}left( {8 — x} right).) Найдем нули производной: ({e^{x + 9}}left( {8 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,8 — x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = 8.) Определим знаки производной функции и её поведение: Следовательно, точка максимума (x = 8.) Ответ: 8. |
| Задача 4. Найдите точку минимума функции (y = left( {25 — x} right){e^{25 — x}})
Ответ
ОТВЕТ: 26. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {25 — x} right)^prime }{e^{25 — x}} + left( {25 — x} right){left( {{e^{25 — x}}} right)^prime } = — {e^{25 — x}} + left( {25 — x} right){e^{25 — x}} cdot {left( {25 — x} right)^prime } = ) ( = — {e^{25 — x}}-left( {25 — x} right){e^{25 — x}} = {e^{25 — x}}left( { — 1 — 25 + x} right) = {e^{25 — x}}left( {x — 26} right).) Найдем нули производной: ({e^{25 — x}}left( {x — 26} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x — 26 = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = 26.) Определим знаки производной функции и её поведение: Следовательно, точка минимума (x = 26.) Ответ: 26. |
| Задача 5. Найдите точку максимума функции (y = left( {x + 9} right){e^{9 — x}})
Ответ
ОТВЕТ: — 8. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {x + 9} right)^prime }{e^{9 — x}} + left( {x + 9} right){left( {{e^{9 — x}}} right)^prime } = {e^{9 — x}} + left( {x + 9} right){e^{9 — x}} cdot {left( {9 — x} right)^prime } = ) ( = {e^{9 — x}} — left( {x + 9} right){e^{9 — x}} = {e^{9 — x}}left( {1 — x — 9} right) = {e^{9 — x}}left( { — x — 8} right).) Найдем нули производной: ({e^{9 — x}}left( { — x — 8} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,left( { — x — 8} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = — 8.) Определим знаки производной функции и её поведение: Следовательно, точка максимума (x = — 8.) Ответ: – 8. |
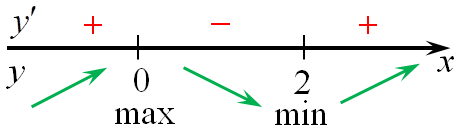
| Задача 6. Найдите точку минимума функции (y = left( {4{x^2} — 16x + 16} right){e^{x — 9}})
Ответ
ОТВЕТ: 2. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {4{x^2} — 16x + 16} right)^prime }{e^{x — 9}} + left( {4{x^2} — 16x + 16} right){left( {{e^{x — 9}}} right)^prime } = left( {8x — 16} right){e^{x — 9}} + left( {4{x^2} — 16x + 16} right){e^{x — 9}} = ) ( = {e^{x — 9}}left( {8x — 16 + 4{x^2} — 16x + 16} right) = {e^{x — 9}}left( {4{x^2} — 8x} right).) Найдем нули производной: ({e^{x — 9}}left( {4{x^2} — 8x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,4{x^2} — 8x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 0,,,,,,,,{x_2} = 2.) Определим знаки производной функции и её поведение: Следовательно, точка минимума (x = 2.) Ответ: 2. |
| Задача 7. Найдите точку максимума функции (y = left( {2{x^2} — 30x + 30} right){e^{x + 9}})
Ответ
ОТВЕТ: 0. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {2{x^2} — 30x + 30} right)^prime }{e^{x + 9}} + left( {2{x^2} — 30x + 30} right){left( {{e^{x + 9}}} right)^prime } = left( {4x — 30} right){e^{x + 9}} + left( {2{x^2} — 30x + 30} right){e^{x + 9}} = ) ( = {e^{x + 9}}left( {4x — 30 + 2{x^2} — 30x + 30} right) = {e^{x + 9}}left( {2{x^2} — 26x} right).) Найдем нули производной: ({e^{x + 9}}left( {2{x^2} — 26x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,2{x^2} — 26x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 0,,,,,,,{x_2} = 13.) Определим знаки производной функции и её поведение: Следовательно, точка максимума (x = 0.) Ответ: 0. |
| Задача 8. Найдите точку максимума функции (y = left( {2{x^2} — 10x + 10} right){e^{36 — x}})
Ответ
ОТВЕТ: 5. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {2{x^2} — 10x + 10} right)^prime }{e^{36 — x}} + left( {2{x^2} — 10x + 10} right){left( {{e^{36 — x}}} right)^prime } = ) ( = left( {4x — 10} right){e^{36 — x}} + left( {2{x^2} — 10x + 10} right){e^{36 — x}} cdot {left( {36 — x} right)^prime } = left( {4x — 10} right){e^{36 — x}} — left( {2{x^2} — 10x + 10} right){e^{36 — x}} = ) ( = {e^{36 — x}}left( {4x — 10 — 2{x^2} + 10x — 10} right) = {e^{36 — x}}left( { — 2{x^2} + 14x — 20} right).) Найдем нули производной: ({e^{36 — x}}left( { — 2{x^2} + 14x — 20} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,, — 2{x^2} + 14x — 20 = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 2,,,,,,,{x_2} = 5.) Определим знаки производной функции и её поведение: Следовательно, точка максимума (x = 5.) Ответ: 5. |
| Задача 9. Найдите точку максимума функции (y = {left( {x — 7} right)^2}{e^{x — 8}})
Ответ
ОТВЕТ: 5. Решение
Найдем производную заданной функции: (y’ = {left( {{{left( {x — 7} right)}^2}} right)^prime }{e^{x — 8}} + {left( {x — 7} right)^2}{left( {{e^{x — 8}}} right)^prime } = 2left( {x — 7} right){e^{x — 8}} + {left( {x — 7} right)^2}{e^{x — 8}} = ) ( = {e^{x — 8}}left( {x — 7} right)left( {2 + x — 7} right) = {e^{x — 8}}left( {x — 7} right)left( {x — 5} right).) Найдем нули производной: ({e^{x — 8}}left( {x — 7} right)left( {x — 5} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,left( {x — 7} right)left( {x — 5} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 5,,,,,,,{x_2} = 7.) Определим знаки производной функции и её поведение: Следовательно, точка максимума (x = 5.) Ответ: 5. |
| Задача 10. Найдите точку минимума функции (y = {left( {x — 2} right)^2}{e^{x — 5}})
Ответ
ОТВЕТ: 2. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x — 2} right)}^2}} right)^prime }{e^{x — 5}} + {left( {x — 2} right)^2}{left( {{e^{x — 5}}} right)^prime } = 2left( {x — 2} right){e^{x — 5}} + {left( {x — 2} right)^2}{e^{x — 5}} = ) ( = {e^{x — 5}}left( {x — 2} right)left( {2 + x — 2} right) = {e^{x — 5}}left( {x — 2} right)x.) Найдем нули производной: ({e^{x — 5}}left( {x — 2} right)x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,,,,{x_1} = 0,,,,,,,{x_2} = 2.) Определим знаки производной функции и её поведение: Следовательно, точка минимума (x = 2.) Ответ: 2. |
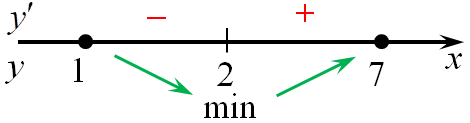
| Задача 11. Найдите точку максимума функции (y = {left( {x — 9} right)^2}{e^{9 — x}})
Ответ
ОТВЕТ: 11. Решение
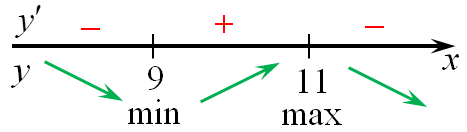
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x — 9} right)}^2}} right)^prime }{e^{9 — x}} + {left( {x — 9} right)^2}{left( {{e^{9 — x}}} right)^prime } = 2left( {x — 9} right){e^{9 — x}} + {left( {x — 9} right)^2}{e^{9 — x}}{left( {9 — x} right)^prime } = ) ( = 2left( {x — 9} right){e^{9 — x}} — {left( {x — 9} right)^2}{e^{9 — x}} = {e^{9 — x}}left( {x — 9} right)left( {2 — x + 9} right) = {e^{9 — x}}left( {x — 9} right)left( {11 — x} right).) Найдем нули производной: ({e^{9 — x}}left( {x — 9} right)left( {11 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,left( {x — 9} right)left( {11 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 9,,,,,,,{x_2} = 11.) Определим знаки производной функции и её поведение: Следовательно, точка максимума (x = 11.) Ответ: 11. |
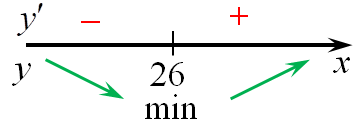
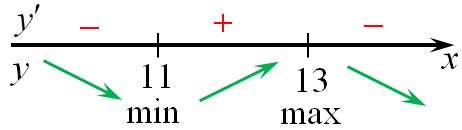
| Задача 12. Найдите точку минимума функции (y = {left( {x — 11} right)^2}{e^{17 — x}})
Ответ
ОТВЕТ: 11. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x — 11} right)}^2}} right)^prime }{e^{17 — x}} + {left( {x — 11} right)^2}{left( {{e^{17 — x}}} right)^prime } = 2left( {x — 11} right){e^{17 — x}} + {left( {x — 11} right)^2}{e^{17 — x}}{left( {17 — x} right)^prime } = ) ( = 2left( {x — 11} right){e^{17 — x}} — {left( {x — 11} right)^2}{e^{17 — x}} = {e^{17 — x}}left( {x — 11} right)left( {2 — x + 11} right) = {e^{17 — x}}left( {x — 11} right)left( {13 — x} right).) Найдем нули производной: ({e^{17 — x}}left( {x — 11} right)left( {13 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,left( {x — 11} right)left( {13 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 11,,,,,,,{x_2} = 13.) Определим знаки производной функции и её поведение: Следовательно, точка минимума (x = 11.) Ответ: 11. |
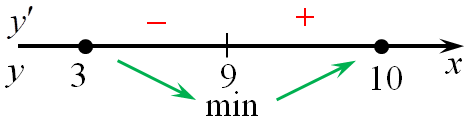
| Задача 13. Найдите наименьшее значение функции (y = left( {8 — x} right){e^{9 — x}}) на отрезке (left[ {3;10} right])
Ответ
ОТВЕТ: — 1. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {8 — x} right)^prime }{e^{9 — x}} + left( {8 — x} right){left( {{e^{9 — x}}} right)^prime } = — {e^{9 — x}} + left( {8 — x} right){e^{9 — x}}{left( {9 — x} right)^prime } = ) ( = -{e^{9 — x}} — left( {8 — x} right){e^{9 — x}} = {e^{9 — x}}left( { — 1 — 8 + x} right) = {e^{9 — x}}left( {x — 9} right).) Найдем нули производной: ({e^{9 — x}}left( {x — 9} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x — 9 = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = 9.) Определим знаки производной функции на отрезке (left[ {3;10} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ {3;10} right]) будет в точке (x = 9.) (yleft( 9 right) = left( {8 — 9} right){e^{9 — 9}} = — 1.) Ответ: – 1. |
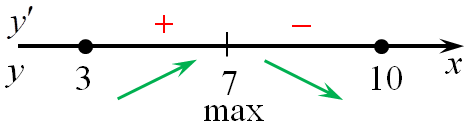
| Задача 14. Найдите наибольшее значение функции (y = left( {8 — x} right){e^{x — 7}}) на отрезке (left[ {3;10} right])
Ответ
ОТВЕТ: 1. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {8 — x} right)^prime }{e^{x — 7}} + left( {8 — x} right){left( {{e^{x — 7}}} right)^prime } = — {e^{x — 7}} + left( {8 — x} right){e^{x — 7}} = {e^{x — 7}}left( { — 1 + 8 — x} right) = {e^{x — 7}}left( {7 — x} right) = 0.) Найдем нули производной: ({e^{x — 7}}left( {7 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,7 — x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = 7.) Определим знаки производной функции на отрезке (left[ {3;10} right]) и её поведение: Следовательно, наибольшее значение функции на отрезке (left[ {3;10} right]) будет в точке (x = 7.) (yleft( 7 right) = left( {8 — 7} right){e^{7 — 7}} = 1.) Ответ: 1. |
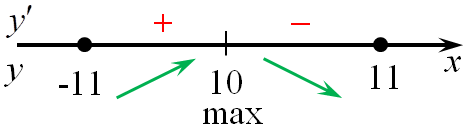
| Задача 15. Найдите наибольшее значение функции (y = left( {x — 9} right){e^{10 — x}}) на отрезке (left[ { — 11;11} right])
Ответ
ОТВЕТ: 1. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {x — 9} right)^prime }{e^{10 — x}} + left( {x — 9} right){left( {{e^{10 — x}}} right)^prime } = {e^{10 — x}} + left( {x — 9} right){e^{10 — x}}{left( {10 — x} right)^prime } = ) ( = {e^{10 — x}} — left( {x — 9} right){e^{10 — x}} = {e^{10 — x}}left( {1 — x + 9} right) = {e^{10 — x}}left( {10 — x} right).) Найдем нули производной: ({e^{10 — x}}left( {10 — x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,10 — x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,x = 10.) Определим знаки производной функции на отрезке (left[ { — 11;11} right]) и её поведение: Следовательно, наибольшее значение функции на отрезке (left[ { — 11;11} right]) будет в точке (x = 10.) (yleft( {10} right) = left( {10 — 9} right){e^{10 — 10}} = 1.) Ответ: 1. |
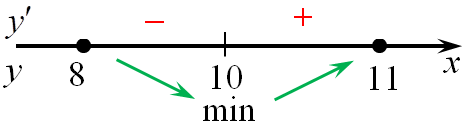
| Задача 16. Найдите наименьшее значение функции (y = left( {3{x^2} — 36x + 36} right){e^{x — 10}}) на отрезке (left[ {8;11} right])
Ответ
ОТВЕТ: — 24. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {3{x^2} — 36x + 36} right)^prime }{e^{x — 10}} + left( {3{x^2} — 36x + 36} right){left( {{e^{x — 10}}} right)^prime } = left( {6x — 36} right){e^{x — 10}} + left( {3{x^2} — 36x + 36} right){e^{x — 10}} = ) ( = {e^{x — 10}}left( {6x — 36 + 3{x^2} — 36x + 36} right) = {e^{x — 10}}left( {3{x^2} — 30x} right).) Найдем нули производной: ({e^{x — 10}}left( {3{x^2} — 30x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,3{x^2} — 30x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 0,,,,,,,,{x_2} = 10.) Значение ({x_1} = 0 notin left[ {8;11} right].) Определим знаки производной функции на отрезке (left[ {8;11} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ {8;11} right]) будет в точке (x = 10.) (yleft( {10} right) = left( {3 cdot {{10}^2} — 36 cdot 10 + 36} right){e^{10 — 10}} = — 24.) Ответ: – 24. |
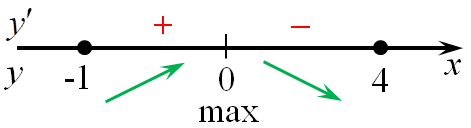
| Задача 17. Найдите наибольшее значение функции (y = left( {3{x^2} — 36x + 36} right){e^x}) на отрезке (left[ { — 1;4} right])
Ответ
ОТВЕТ: 36. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {3{x^2} — 36x + 36} right)^prime }{e^x} + left( {3{x^2} — 36x + 36} right){left( {{e^x}} right)^prime } = left( {6x — 36} right){e^x} + left( {3{x^2} — 36x + 36} right){e^x} = ) ( = {e^x}left( {6x — 36 + 3{x^2} — 36x + 36} right) = {e^x}left( {3{x^2} — 30x} right).) Найдем нули производной: ({e^x}left( {3{x^2} — 30x} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,3{x^2} — 30x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 0,,,,,,,,{x_2} = 10.) Значение ({x_2} = 10 notin left[ { — 1;4} right].) Определим знаки производной функции на отрезке (left[ { — 1;4} right]) и её поведение: Следовательно, наибольшее значение функции на отрезке (left[ { — 1;4} right]) будет в точке (x = 0.) (yleft( 0 right) = left( {3 cdot {0^2} — 36 cdot 0 + 36} right){e^0} = 36.) Ответ: 36. |
| Задача 18. Найдите наименьшее значение функции (y = left( {{x^2} — 8x + 8} right){e^{2 — x}}) на отрезке (left[ {1;7} right])
Ответ
ОТВЕТ: — 4. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{x^2} — 8x + 8} right)^prime }{e^{2 — x}} + left( {{x^2} — 8x + 8} right){left( {{e^{2 — x}}} right)^prime } = left( {2x — 8} right){e^{2 — x}} + left( {{x^2} — 8x + 8} right){e^{2 — x}} cdot {left( {2 — x} right)^prime } = ) ( = left( {2x — 8} right){e^{2 — x}} — left( {{x^2} — 8x + 8} right){e^{2 — x}} = {e^{2 — x}}left( {2x — 8 — {x^2} + 8x — 8} right) = {e^{2 — x}}left( { — {x^2} + 10x — 16} right).) Найдем нули производной: ({e^{2 — x}}left( { — {x^2} + 10x — 16} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,, — {x^2} + 10x — 16 = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 2,,,,,,,,{x_2} = 8.) Значение ({x_2} = 8 notin left[ {1;7} right].) Определим знаки производной функции на отрезке (left[ {1;7} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ {1;7} right]) будет в точке (x = 2.) (yleft( 2 right) = left( {{2^2} — 8 cdot 2 + 8} right){e^{2 — 2}} = — 4.) Ответ: – 4. |
| Задача 19. Найдите наибольшее значение функции (y = left( {{x^2} — 10x + 10} right){e^{10 — x}}) на отрезке (left[ {5;11} right])
Ответ
ОТВЕТ: 10. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{x^2} — 10x + 10} right)^prime }{e^{10 — x}} + left( {{x^2} — 10x + 10} right){left( {{e^{10 — x}}} right)^prime } = ) ( = left( {2x — 10} right){e^{10 — x}} + left( {{x^2} — 10x + 10} right){e^{10 — x}} cdot {left( {10 — x} right)^prime } = left( {2x — 10} right){e^{10 — x}} — left( {{x^2} — 10x + 10} right){e^{10 — x}} = ) ( = {e^{10 — x}}left( {2x — 10 — {x^2} + 10x — 10} right) = {e^{10 — x}}left( { — {x^2} + 12x — 20} right).) Найдем нули производной: ({e^{10 — x}}left( { — {x^2} + 12x — 20} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 2,,,,,,,,{x_2} = 10.) Значение ({x_2} = 2 notin left[ {5;11} right].) Определим знаки производной функции на отрезке (left[ {5;11} right]) и её поведение: Следовательно, наибольшее значение функции на отрезке (left[ {5;11} right]) будет в точке (x = 10.) (yleft( {10} right) = left( {{{10}^2} — 10 cdot 10 + 10} right){e^{10 — 10}} = 10.) Ответ: 10. |
| Задача 20. Найдите наименьшее значение функции (y = {left( {x — 2} right)^2}{e^{x — 2}}) на отрезке (left[ {1;4} right])
Ответ
ОТВЕТ: 0. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x — 2} right)}^2}} right)^prime }{e^{x — 2}} + {left( {x — 2} right)^2}{left( {{e^{x — 2}}} right)^prime } = 2left( {x — 2} right){e^{x — 2}} + {left( {x — 2} right)^2}{e^{x — 2}} = ) ( = {e^{x — 2}}left( {x — 2} right)left( {2 + x — 2} right) = {e^{x — 2}}left( {x — 2} right)x.) Найдем нули производной: ({e^{x — 2}}left( {x — 2} right)x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 0,,,,,,,,{x_2} = 2.) Значение ({x_1} = 0 notin left[ {1;4} right].) Определим знаки производной функции на отрезке (left[ {1;4} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ {1;4} right]) будет в точке (x = 2.) (yleft( 2 right) = {left( {2 — 2} right)^2}{e^{2 — 2}} = 0.) Ответ: 0. |
| Задача 21. Найдите наибольшее значение функции (y = {left( {x — 2} right)^2}{e^x}) на отрезке (left[ { — 5;1} right])
Ответ
ОТВЕТ: 4. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x — 2} right)}^2}} right)^prime }{e^x} + {left( {x — 2} right)^2}{left( {{e^x}} right)^prime } = 2left( {x — 2} right){e^x} + {left( {x — 2} right)^2}{e^x} = {e^x}left( {x — 2} right)left( {2 + x — 2} right) = {e^x}left( {x — 2} right)x.) Найдем нули производной: ({e^x}left( {x — 2} right)x = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = 0,,,,,,,,{x_2} = 2.) Значение ({x_2} = 2 notin left[ { — 5;1} right].) Определим знаки производной функции на отрезке (left[ { — 5;1} right]) и её поведение: Следовательно, наибольшее значение функции на отрезке (left[ { — 5;1} right]) будет в точке (x = 0.) (yleft( 0 right) = {left( {0 — 2} right)^2}{e^0} = 4.) Ответ: 4. |
| Задача 22. Найдите наименьшее значение функции (y = {left( {x + 3} right)^2}{e^{ — 3 — x}}) на отрезке (left[ { — 5;, — 1} right])
Ответ
ОТВЕТ: 0. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x + 3} right)}^2}} right)^prime }{e^{ — 3 — x}} + {left( {x + 3} right)^2}{left( {{e^{ — 3 — x}}} right)^prime } = 2left( {x + 3} right){e^{ — 3 — x}} + {left( {x + 3} right)^2}{e^{ — 3 — x}} cdot {left( { — 3 — x} right)^prime } = ) ( = 2left( {x + 3} right){e^{ — 3 — x}} — {left( {x + 3} right)^2}{e^{ — 3 — x}} = {e^{ — 3 — x}}left( {x + 3} right)left( {2 — x — 3} right) = {e^{ — 3 — x}}left( {x + 3} right)left( { — x — 1} right).) Найдем нули производной: ({e^{ — 3 — x}}left( {x + 3} right)left( { — x — 1} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = — 3,,,,,,,,{x_2} = — 1.) Определим знаки производной функции на отрезке (left[ { — 5; — 1} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ { — 5; — 1} right]) будет в точке (x = — 3.) (yleft( { — 3} right) = {left( { — 3 + 3} right)^2}{e^{ — 3 + 3}} = 0.) Ответ: 0. |
| Задача 23. Найдите наибольшее значение функции (y = {left( {x + 6} right)^2}{e^{ — 4 — x}}) на отрезке (left[ { — 6; — 1} right])
Ответ
ОТВЕТ: 4. Решение
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{{left( {x + 6} right)}^2}} right)^prime }{e^{ — 4 — x}} + {left( {x + 6} right)^2}{left( {{e^{ — 4 — x}}} right)^prime } = 2left( {x + 6} right){e^{ — 4 — x}} + {left( {x + 6} right)^2}{e^{ — 4 — x}} cdot {left( { — 4 — x} right)^prime } = ) ( = 2left( {x + 6} right){e^{ — 4 — x}} — {left( {x + 6} right)^2}{e^{ — 4 — x}} = {e^{ — 4 — x}}left( {x + 6} right)left( {2 — x — 6} right) = {e^{ — 4 — x}}left( {x + 6} right)left( { — x — 4} right).) Найдем нули производной: ({e^{ — 4 — x}}left( {x + 6} right)left( { — x — 4} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,{x_1} = — 6,,,,,,,,{x_2} = — 4.) Определим знаки производной функции на отрезке (left[ { — 6; — 1} right]) и её поведение: Следовательно, наибольшее значение функции на отрезке (left[ { — 6; — 1} right]) будет в точке (x = — 4.) (yleft( { — 4} right) = {left( { — 4 + 6} right)^2}{e^{ — 4 + 4}} = 4.) Ответ: 4. |
| Задача 24. Найдите наименьшее значение функции ({e^{2x}} — 6{e^x} + 3) на отрезке (left[ {1;2} right])
Ответ
ОТВЕТ: — 6. Решение
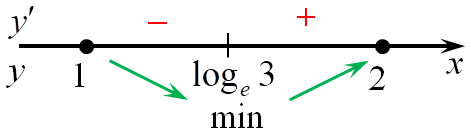
Область определения функции: (x, in ,R.) Найдем производную заданной функции: (y’ = {left( {{e^{2x}}} right)^prime } — {left( {6{e^x}} right)^prime } + 3 = {e^{2x}} cdot {left( {2x} right)^prime } — 6{e^x} = 2{e^{2x}} — 6{e^x}.) Найдем нули производной: (2{e^{2x}} — 6{e^x} = 0,,,,,,,, Leftrightarrow ,,,,,,,{e^x}left( {2{e^x} — 6} right) = 0,,,,,,,, Leftrightarrow ,,,,,,,,,2{e^x} — 6 = 0,,,,,,,,, Leftrightarrow ,,,,,,,x = {log _e}3.) Определим знаки производной функции на отрезке (left[ {1;2} right]) и её поведение: Следовательно, наименьшее значение функции на отрезке (left[ {1;2} right]) будет в точке (x = {log _e}3.) (yleft( {{{log }_e}3} right) = {e^{2{{log }_e}3}} — 6 cdot {e^{{{log }_e}3}} + 3 = {e^{{{log }_e}9}} — 6 cdot 3 + 3 = 9 — 18 + 3 = — 6.) Ответ: – 6. |
ЕГЭ 2023
Варианты ЕГЭ 2023 базового уровня
ЕГЭбаз 2023 №01-12
ЕГЭбаз 2023 №13-24 в VK по платной подписке
Задачники ЕГЭ 2023 базового уровня
Задание 01. Текстовые задачи (простейшие)
Задание 02. Размеры и единицы измерения
Задание 03. Графики и диаграммы
Задание 04. Преобразование выражений (формулы)
Задание 05. Теория вероятностей
Задание 06. Выбор оптимального варианта
Задание 07. Анализ графиков и таблиц
Задание 08. Анализ утверждений
Задание 09. Площадь
Задание 10. Прикладная планиметрия
Задание 11. Прикладная стереометрия
Задание 12. Планиметрия
Задание 13. Стереометрия
Задание 14. Действия с дробями
Задание 15. Текстовые задачи (проценты)
Задание 16. Вычисления и преобразования
Задание 17. Уравнения
Задание 18. Числа и неравенства
Задание 19. Цифровая запись числа
Задание 20. Текстовая задача
Внимание!
Скачивая материалы с этого сайта, Вы принимаете условия
Пользовательского Соглашения!
Варианты ЕГЭ 2023 профильного уровня
ЕГЭпроф 2023 №01-10
ЕГЭпроф 2023 №11-24 в VK по платной подписке
Задачники ЕГЭ 2023 профильного уровня
Задание 01. Планиметрия
Задание 02. Стереометрия
Задание 03. Теория вероятностей
Задание 04. Теория вероятностей (повыш. сложность)
Задание 05. Простейшие уравнения
Задание 06. Значение выражения
Задание 07. Производная и первообразная
Задание 08. Задачи с прикладным содержанием
Задание 09. Текстовые задачи
Задание 10. Функции
Задание 11. Исследование функций
Задание 12. Уравнения
Задание 13. Стереометрия
Задание 14. Неравенства
Задание 15. Финансовая математика
Задание 16. —-
Задание 17. —-
Задание 18. —-
ОТВЕТЫ к Задачникам ЕГЭ 2023 года
МАТЕРИАЛЫ прошлых лет (ЕГЭ АРХИВ)
Задание 21. Задачи на смекалку
Вариант и ответы с пробника ЕГЭ 2023 по математике профиль, который прошёл 3 декабря 2022 года у 11 класса школьников Москвы. Единая городская контрольная работа в формате ЕГЭ по математике профильный уровень.
скачать вариант №1
скачать вариант №2
пробник-егэ2023-профиль-математика
Видео разбор заданий варианта ЕГЭ
1. Дан равнобедренный треугольник 𝐴𝐵𝐶 с основанием 𝐴𝐶 и боковой стороной длины 7. Точка 𝐾 на стороне 𝐵𝐶 такая, что 𝐾𝐶 = 3, 𝑆𝐴𝐵𝐶 = 14. Найдите площадь треугольника 𝐴𝐵𝐾.
2. Имеется банка в форме цилиндра. Из неё перелили сок в 40 цилиндрических стаканов. Диаметр одного стакана в 4 раза меньше диаметра банки. При этом уровень сока в каждом стакане оказался 8 см. Какой была высота уровня сока в банке? Ответ дайте в сантиметрах.
3. В сборнике 4 билета по теме «Механические колебания». Вероятность того, что ученику попадётся билет не по данной теме равна 0,9. Сколько всего билетов в сборнике?
4. Стрелок стреляет по мишеням 5 раз. Вероятность попадания каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события, что стрелок попадёт в цель 4 раза больше вероятности события, что он попадёт в цель 3 раза?
5. Найдите корень уравнения √3 34 − 3𝑥 = 4.
8. Полная энергия падающего тела вычисляется по формуле 𝐸пол = 𝑚𝑣2 2 +𝑚𝑔ℎ. С какой скоростью двигалось тело массой 3 кг в момент, когда оно находилось на высоте 1,5 м, если его полная энергия в этот момент составляла 68,1 Дж? Ускорение свободного падения 𝑔 = 9,8 м/c2 .
9. Из двух городов, расстояние между которыми 720 км, выехали навстречу друг другу два поезда. Второй поезд выехал на час позже первого и едет со скоростью на 4 км/ч больше скорости первого. Поезда встретились ровно в середине пути. Найдите скорость первого поезда.
10. Дан график 𝑓(𝑥) = ⃒ ⃒𝑎𝑥2 + 𝑏𝑥 + 𝑐 ⃒ ⃒ , где 𝑎, 𝑏, 𝑐 – целые числа. Найдите 𝑓(4).
13. В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 на ребре 𝐴𝐴1 отмечена точка 𝐸 так, что 𝐴1𝐸 : 𝐸𝐴 = 3 : 2. Точка 𝑇 — середина ребра 𝐵1𝐶1, 𝐴𝐴1 = 10 и 𝐴𝐷 = 6. а) Докажите, что сечение параллелепипеда плоскостью 𝐸𝑇 𝐷1 – равнобедренная трапеция. б) Найдите площадь сечения параллелепипеда плоскостью 𝐸𝑇 𝐷1, если 𝐴𝐵 = 2√ 10.
15. В банке можно открыть один из двух вкладов. По вкладу А в конце каждого из трёх лет начисляется по 20% от суммы вклада в начале года. По вкладу Б в конце каждого из первых двух лет начисляется по 22% от суммы вклада в начале года. При каком наименьшем целом количестве начисляемых за третий год процентов по вкладу Б, вклад Б будет выгоднее вклада А?
16. Дан прямоугольный треугольник 𝐴𝐵𝐶. Квадрат 𝐶𝐾𝑁𝑀, такой, что точки 𝐾 и 𝑀 лежат на катетах 𝐴𝐶 и 𝐵𝐶 соответственно, а 𝑁 лежит на гипотенузе 𝐴𝐵. Квадрат 𝑃 𝑄𝑅𝑇 такой, что вершины 𝑃 и 𝑄 лежат на 𝐴𝐶 и 𝐵𝐶, а вершины 𝑇 и 𝑅 лежат на гипотенузе. а) Докажите, что точки 𝐶, 𝑁 и центры квадратов лежат на одной прямой. б) Найти сторону квадрата 𝑃 𝑄𝑅𝑇, если 𝐴𝐶 = 12 и 𝐵𝐶 = 5.
17. Найдите все значения а, при каждом из которых неравенство 𝑎(𝑎 − 7,5) − 2(𝑎 − 7,5) (2𝑥 + 2) 6 (︀ 2𝑥 2 − 3𝑥 )︀ (2𝑥 + 2) − 𝑎𝑥2 + 1,5𝑎𝑥 имеет хотя бы 1 решение на промежутке [−1; 0).
18. Пусть {𝑎𝑛} – последовательность натуральных чисел. Обозначим 𝑀<𝐶(𝑎𝑛) – среднее арифметическое всех членов последовательности {𝑎𝑛}, которые меньше некоторого числа 𝐶. Число 𝐶 лежит между наибольшим и наименьшим членами последовательности. Обозначим 𝑀>𝐶(𝑎𝑛) – среднее арифметическое всех членов последовательности {𝑎𝑛}, которые больше или равны 𝐶. Среднее арифметическое одного числа равно самому числу. Затем к каждому члену последовательности {𝑎𝑛} прибавили 4 и получили новую последовательность, которую обозначили {𝑎𝑛 + 4}.
- a) Существует ли последовательность {𝑎𝑛}, состоящая из трех членов, для которой 𝑀<79 (𝑎𝑛 + 4) < 𝑀<79 (𝑎𝑛)?
- б) Существует ли последовательность {𝑎𝑛}, состоящая из трех членов, для которой 𝑀<79 (𝑎𝑛 + 4) < 𝑀<79 (𝑎𝑛) и 𝑀>79 (𝑎𝑛 + 4) < 𝑀>79 (𝑎𝑛)?
- в) Известно, что среднее арифметическое всех членов последовательности {𝑎𝑛} равняется 84, 𝑀>79 (𝑎𝑎) = 94, 𝑀<79 (𝑎𝑛) = 70, 𝑀>79 (𝑎𝑛 + 4) = 96 и 𝑀<79 (𝑎𝑛 + 4) = 72. Какое наименьшее число членов может быть в последовательности {𝑎𝑛} ?
2 версия варианта
03122022
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Джинни и Джорджия 1-2 сезон смотреть онлайн
После смерти своего мужа 30 летняя женщина Джорджия Миллер решает начать жизнь с чистого листа. Поэтому она решает переехать в Новую Англию вместе со своими детьми, дочерью Джинни и сыном Остином. Устав от многочисленных переездов, дети искренне желают наконец-то осесть на одном месте и жить, не оглядываясь на прошлое своей матери. Джорджия из-за своих прошлых ошибок вынуждена постоянно менять место жительство. Разный взгляд на будущее приводит к разногласиям и конфликтам между женщиной и её детьми. Несмотря на все неурядицы, Новая Англия понравилась Джинни некоторыми перспективами, поскольку именно здесь юной девушке представилась возможность учиться в элитной школе и общаться с интересными людьми.
Поскольку Джорджия совершила большое количество ошибок в прошлом, она всячески стремится оградить детей от необдуманных поступков и решений. Несмотря на это, женщина до сих пор считает себя молодой девушкой. Поэтому она желает найти того единственного мужчину, с которым она смогла бы прожить всю свою жизнь. Такое легкомысленное поведение матери пугает Джинни, ведь Джорджия всё больше времени, сил и внимания уделяет новым ухажёрам. К каким последствиям приведёт такое поведение женщины?
- Оригинальное название: Ginny & Georgia
- Год выхода: 2021
- Страна: США
- Премьера: 24 февраля 2021
- Режиссер: Аня Адамс, Каталина Агиляр Мастретта, Renuka Jeyapalan
- Перевод: TVShows
- Качество: FHD (1080p)
- Статус сериала: На паузе
-
7.5
7.4
- Актеры: Брианна Хоуи, Антония Джентри, Дизель Ла Торрака, Дженнифер Робертсон, Феликс Маллард, Сара Вайсгласс, Скотт Портер, Реймонд Эблэк, Mason Temple, Кэти Дуглас
- Канал: Netflix
- Жанр: Драма, Комедия
«Джинни и Джорджия» смотреть онлайн бесплатно в хорошем качестве
Смотреть онлайн
Плеер 2
Трейлер
Свет
Добавить в закладки
Подписывайтесь на нашу группу в VK