Задания
Версия для печати и копирования в MS Word
Задания Д4 № 27888
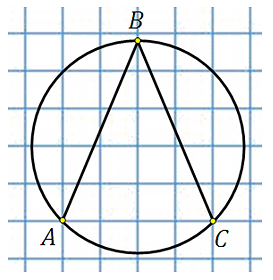
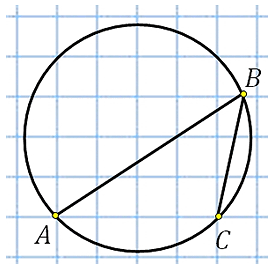
Найдите величину угла
Ответ дайте в градусах.
Спрятать решение
Решение.
Центральный угол, опирающийся на хорду АС равен 90°, поэтому меньшая дуга окружности, отсекаемая этой хордой, также равна 90°, а большая — равна 270°. Опирающийся на нее вписанный угол ABC равен ее половине т. е. 135°.
Ответ: 135.
Аналоги к заданию № 27887: 27888 27889 26234 26235 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.1.4 Окружность и круг, 5.1.5 Вписанная и описанная окружность треугольника, 5.5.1 Величина угла, градусная мера угла
Спрятать решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-13

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Тема 25.
Программирование — Обработка целочисленной информации
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
программирование — обработка целочисленной информации
25.01Маска числа
25.02Поиск делителей
25.03Числа-палиндромы
25.04Простые числа
25.05Прочие прототипы
Решаем задачу:
Пусть M — сумма минимального и максимального натурального делителей целого числа, не считая единицы и самого числа.
Если таких делителей нет, то считаем значение M равным нулю.
Напишите программу, которая перебирает целые числа, большие 452 021, в порядке возрастания и ищет среди них
такие, для которых значение М при делении на 7 дает в остатке 3. Вывести первые 5 найденных чисел и соответствующие
им значения М.
Показать ответ и решение
def m(n):
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return i + n // i
return 0
k = 0
for i in range(452021 + 1, 10000000000000):
if m(i) % 7 == 3:
print(i, m(i))
k += 1
if k == 5: break
Ответ:
452025 150678 452029 23810 452034 226019 452048 226026 452062 226033
Дата: 2016-01-26
21416
Категория: Вписанный угол
Метка: ЕГЭ-№1ОкружностьУглы
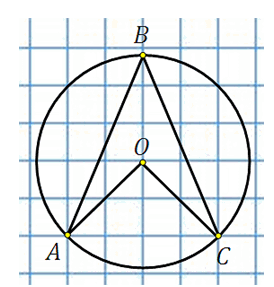
27887. Найдите величину угла ABC. Ответ дайте в градусах.
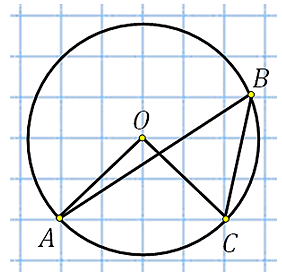
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 900. Это видно по тому как проходят АО и ОС относительно клетчатой сетки. Угол АВС это вписанный угол, построенный на той же дуге.
По свойству вписанного угла:
Ответ: 45
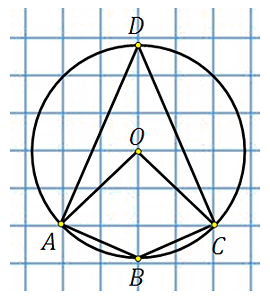
27888. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС и вписанный угол ADC:
Центральный угол АОС равен 900. По свойству вписанного угла
Известно, что у четырёхугольника вписанного в окружность сумма противоположных углов равна 180 градусам, следовательно:
Ответ: 135
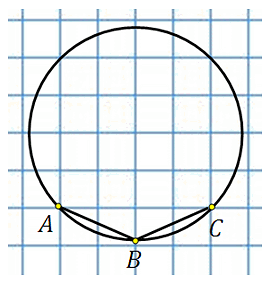
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности (видно о клетчатой сетке). Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 90 градусов. Угол АВС это вписанный угол, построенный на той же дуге. По свойству вписанного угла:
Ответ: 45
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
WEB-DL
- Год выхода: 2019
- Страна: Россия
- Жанр: Комедия
- Режиссер: Константин Смирнов, Константин Колесов
- Актёры: Вячеслав Чепурченко, Павел Комаров, Вадим Дубровин, Максим Лагашкин, Екатерина Стулова
- Сезоны: 1-3 сезон
- Серии: 1-16 серия
- Время: 00:30
Никита, Дэн и Артемий разработали уникальное приложение для смартфонов, вот-вот продадут его и осуществят все свои мечты. Но в последний момент многомиллионная сделка срывается и парней забирают в армию. Чтобы не ставить под угрозу успех своего стартапа, они выбирают альтернативную службу в глухой деревне Жуки, где будут пытаться довести свой проект до конца. Только не так просто разрабатывать приложение там, где нет даже интернета…
Смотреть онлайн Жуки (2019) в хорошем качестве HD
Плеер 1
Плеер 2
В закладки
Решение 18 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
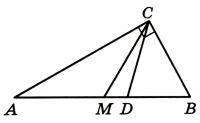
Угол между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C треугольника ABC, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
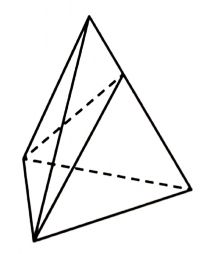
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шашистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шашистом из России.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Найдите корень уравнения (log_4{2^{5x+7}}=3).
Найдите значение выражения (dfrac{a^{3{,}33}}{a^{2{,}11}cdot a^{2{,}22}}) при (a=dfrac{2}{7}).
Прямая (y=9x+6) является касательной к графику (y=ax^2-19x+13). Найдите (a).
Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400) км − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Первый садовый насос перекачивает 10 литров воды за 5 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литров воды?
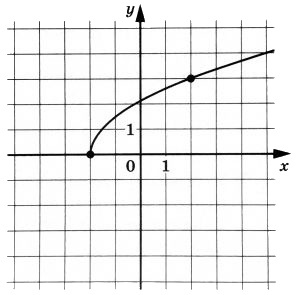
На рисунке изображен график функции (f(x)=ksqrt{x+p}). Найдите (f(0{,}25)).
Найдите наибольшее значение функции (y=2x^2-12x+8ln{x}-5) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right]).
а) Решите уравнение (7cos{x}-4cos^3{x}=2sqrt{3}sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-4pi;-3piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π |
Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=2AC.
Решите неравенство (log^2_{5}{left(x^4right)}-28log_{0{,}04}{left(x^2right)}leqslant 8).
Производство (x) тыс. единиц продуктции обходится в (q=3x^2+6x+13) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении (x)?
Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB=AC=17 и BC=16. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-a+3right)^2+left(y+a-2right)^2=a+dfrac{7}{2}, x-y=a-1 end{cases})имеет единственное решение.
Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{5}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{8}right]+left[dfrac{n}{23}right]=n+2021)?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
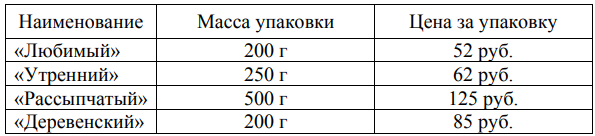
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
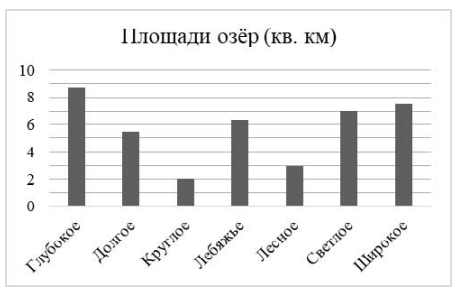
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
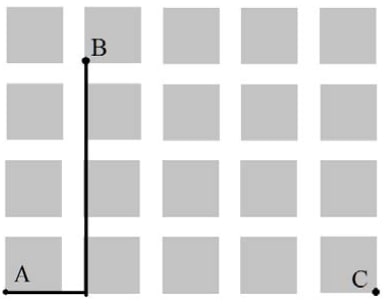
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Установите соответствие между методами и уровнями научного познания: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
МЕТОДЫ
А) наблюдение
Б) эксперимент
В) описание объекта
Г) объяснение существующих взаимосвязей
Д) формулирование закономерностей
УРОВНИ НАУЧНОГО ПОЗНАНИЯ
1) эмпирический
2) теоретический
Пояснение.
А) Наблюдение. Эмпирический. Подразумевает непосредственное взаимодействие с объектом.
Б) Эксперимент. Эмпирический. Подразумевает непосредственное взаимодействие с объектом.
В) Описание объекта. Эмпирический. Подразумевает непосредственное взаимодействие с объектом.
Г) Объяснение существующих взаимосвязей. Теоретический. Подразумевает выявление фундаментальных закономерностей.
Д) Формулирование закономерностей. Теоретический. Подразумевает выявление фундаментальных закономерностей.
Ответ: 11122.
Установите соответствие между примерами и видами налогов и сборов в РФ (в соответствии с Налоговым кодексом РФ): к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ПРИМЕРЫ
А) сборы за пользование объектами животного мира
Б) налог на доходы физических лиц
В) водный налог
Г) торговый сбор
Д) транспортный налог
ВИДЫ НАЛОГОВИ СБОРОВ В РФ
1) федеральные
2) местные
3) региональные
Пояснение.
А) Сборы за пользование объектами животного мира. Федеральные. Зафиксировано в ст. 13 НК РФ.
Б) Налог на доходы физических лиц. Федеральные. Зафиксировано в ст. 13 НК РФ.
В) Водный налог. Федеральные. Зафиксировано в ст. 13 НК РФ.
Г) Торговый сбор. Местные. Зафиксировано в ст. 15 НК РФ.
Д) Транспортный налог. Региональные. Зафиксировано в ст. 14 НК РФ.
Ответ: 11123.
Выберите верные суждения о человеке и запишите цифры, под которыми они указаны.
1) Последовательность стадий жизни человека, при которой детство сменяется юностью, юность — зрелостью, а затем наступает старость, биологически обусловлена.
2) Становление человека как личности связано с приобретением социальных черт и качеств.
3) Человек наследует моральные нормы.
4) Влияние генетических факторов на развитие способностей человека служит выражением его социальной сущности.
5) Природная предрасположенность человека к тем или иным видам деятельности проявляется в социальных обстоятельствах.
Пояснение.
1) Последовательность стадий жизни человека, при которой детство сменяется юностью, юность — зрелостью, а затем наступает старость, биологически обусловлена. Да, верно. Это особенность организма человека.
2) Становление человека как личности связано с приобретением социальных черт и качеств. Да, верно. Они обретаются в процессе социализации.
3) Человек наследует моральные нормы. Нет, неверно. Он усваивает их в процессе социализации.
4) Влияние генетических факторов на развитие способностей человека служит выражением его социальной сущности. Нет, неверно. Это биологическая сущность человека.
5) Природная предрасположенность человека к тем или иным видам деятельности проявляется в социальных обстоятельствах. Да, верно. Задатки развиваются в способности в определенных социальных условиях.
Ответ: 125.
Выберите верные суждения о правоохранительных органах и запишите цифры, под которыми они указаны.
1) Одна из функций правоохранительных органов — укрепление законности и правопорядка.
2) Единая централизованная система федеральных органов, осуществляющих надзор за точным и единообразным исполнением законов, называется адвокатура.
3) Правоохранительные органы могут принимать соответствующие законы.
4) На полицию возложены задачи выявления и расследования преступлений.
5) В ходе судебного производства по уголовному делу прокурор поддерживает государственное обвинение, обеспечивая его законность и обоснованность.
Пояснение.
1) Одна из функций правоохранительных органов — укрепление законности и правопорядка. Да, верно. Это их прямая задача.
2) Единая централизованная система федеральных органов, осуществляющих надзор за точным и единообразным исполнением законов, называется адвокатура. Нет, неверно. Это Прокуратура РФ.
3) Правоохранительные органы могут принимать соответствующие законы. Нет, неверно. Только законодательные органы могут это делать.
4) На полицию возложены задачи выявления и расследования преступлений. Да, верно. В соответствии с 12 статьей ФЗ «О полиции».
5) В ходе судебного производства по уголовному делу прокурор поддерживает государственное обвинение, обеспечивая его законность и обоснованность. Да, верно. Это одна из его обязанностей.
Ответ: 145.
Экспедиция медленно продвигалась в джунглях. Учёные описывали растения, насекомых, животных и птиц, встречавшихся на пути, брали пробы воды и грунта. Так они прибыли в индейскую деревню, где сняли фильм об обычаях аборигенов. Какие из перечисленных ниже методов использовали учёные в приведённой ситуации? Запишите цифры, под которыми они указаны.
1) наблюдение
2) эксперимент
3) моделирование
4) конкретизация
5) эмпирическое описание
6) абстрагирование
Выберите верные суждения о валовом внутреннем продукте (ВВП) и запишите цифры, под которыми они указаны.
1) ВВП — это совокупность экономических ресурсов, включающая ключевые производственные факторы.
2) ВВП отражает общественную потребность в определённом количестве товаров и услуг, необходимых для нормального жизнеобеспечения населения.
3) ВВП характеризует общий объем производства.
4) ВВП — это совокупная рыночная стоимость всех конечных продуктов, произведенных в экономике (внутри страны) в течение одного года.
5) ВВП — это система социально-экономических и юридических отношений, обеспечивающих непрерывный процесс воспроизводства рабочей силы.
Пояснение.
1) ВВП — это совокупность экономических ресурсов, включающая ключевые производственные факторы. — нет, неверно, это не относится к ВВП.
2) ВВП отражает общественную потребность в определённом количестве товаров и услуг, необходимых для нормального жизнеобеспечения населения — нет, неверно, это не относится к ВВП.
3) ВВП характеризует общий объем производства — да, верно.
4) ВВП — это совокупная рыночная стоимость всех конечных продуктов, произведенных в экономике (внутри страны) в течение одного года. — да, верно.
5) ВВП — это система социально-экономических и юридических отношений, обеспечивающих непрерывный процесс воспроизводства рабочей силы — нет, неверно, это не относится к ВВП.
Ответ: 34.
Установите соответствие между видом банка и банковскими функциями: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ФУНКЦИИ БАНКОВ
А) денежная эмиссия
Б) кредитование предприятий
В) мобилизация свободных денежных средств населения
Г) хранение золотовалютных резервов
Д) расчетно-кассовое обслуживание клиентов
ВИДЫ БАНКОВ
1) Банк России
2) коммерческие банки
Пояснение.
Банк России выполняет следующие функции: выпускает деньги (эмиссия), хранит золото, устанавливает ставки рефинансирования и минимальную резервную ставку.
А) денежная эмиссия — Банк России.
Б) кредитование предприятий — коммерческие банки.
В) мобилизация свободных денежных средств населения — коммерческие банки.
Г) хранение золотовалютных резервов — Банк России.
Д) расчетно-кассовое обслуживание клиентов — коммерческие банки.
Ответ: 12212.
Индивидуальный предприниматель Семён за год получил доход в размере 2 млн рублей при затратах 950 тыс. рублей. 120 тыс. рублей он заплатил в качестве налога на доход, и ещё 25 тыс. рублей в качестве налога на имущество. На оставшиеся после уплаты налогов средства Семён приобрёл акции нефтяной компании, рассчитывая на высокие дивиденды. Какие экономические термины характеризуют описанную ситуацию? Запишите цифры, под которыми они указаны.
Цифры укажите в порядке возрастания.
1) макроэкономика
2) налоговый вычет
3) прибыль
4) косвенные налоги
5) прямые налоги
6) инвестиции
Пояснение.
1) макроэкономика — нет, неверно, данные процессы характерны для микроэкономики.
2) налоговый вычет — нет, неверно, в задании не указано, что он вернул часть уплаченных налогов обратно на каком-либо основании.
3) прибыль — да, верно, есть в примере (2 млн дохода при 950 тыс. затрат).
4) косвенные налоги — нет, неверно.
5) прямые налоги — да, верно, налог на доход и налог на имущество.
6) инвестиции — да, верно, Семен инвестировал часть прибыли в акции.
Ответ: 356.
Выберите верные суждения о чертах, присущих демократическим выборам. И запишите цифры, под которыми они указаны.
1) Лица, награждённые государственными наградами, при голосовании имеют два голоса.
2) Законодательно закрепляется, что по результатам выборов в парламент должно пройти не менее двух политических партий.
3) Избиратели голосуют непосредственно за кандидатов на выборные должности.
4) Чтобы зарегистрироваться кандидатом на выборах, необходимо предоставить положительную характеристику с места работы.
5) На избирательных участках обеспечивается тайна голосования.
Пояснение.
1) Лица, награждённые государственными наградами, при голосовании имеют два голоса. Нет, неверно. Один из принципов демократических выборов — равенство голосов избирателей.
2) Законодательно закрепляется, что по результатам выборов в парламент должно пройти не менее двух политических партий. Да, верно. Это исключает возможность установления однопартийности.
3) Избиратели голосуют непосредственно за кандидатов на выборные должности. Да, верно. Это отражает принцип прямых выборов (голосование не за выборщиков, а за кандидатов).
4) Чтобы зарегистрироваться кандидатом на выборах, необходимо предоставить положительную характеристику с места работы. Нет, неверно. Это нарушает принцип независимости кандидатов.
5) На избирательных участках обеспечивается тайна голосования. Да, верно. Это принцип демократических выборов.
Ответ: 235.
Конституция провозглашает государство Z демократическим правовым социальным государством. Какие из приведённых положений Конституции характеризуют Z как социальное государство?
1) Государственная власть разделяется на законодательную, исполнительную и судебную.
2) Каждый имеет право на объединение, включая право создавать профессиональные союзы для защиты своих интересов.
3) Мужчина и женщина имеют равные права и свободы и равные возможности для их реализации.
4) Каждый имеет право на жилище. Никто не может быть произвольно лишён жилища.
5) Каждый имеет право на охрану здоровья и медицинскую помощь.
6) Материнство и детство, семья находятся под защитой государства.
Пояснение.
Необходимо выделить признаки социального государства:
1) Государственная власть разделяется на законодательную, исполнительную и судебную — нет, неверно, это признак правового государства.
2) Каждый имеет право на объединение, включая право создавать профессиональные союзы для защиты своих интересов — нет, неверно, это признак демократического государства.
3) Мужчина и женщина имеют равные права и свободы и равные возможности для их реализации — нет, неверно, это признак правового государства.
4) Каждый имеет право на жилище. Никто не может быть произвольно лишён жилища — да, верно, так как это отражает принцип социального государства, политика которого направлена на создание условий, обеспечивающих достойную жизнь и свободное развитие человека.
5) Каждый имеет право на охрану здоровья и медицинскую помощь — да, верно, так как это отражает принцип социального государства, политика которого направлена на создание условий, обеспечивающих достойную жизнь и свободное развитие человека.
6) Материнство и детство, семья находятся под защитой государства — да, верно, так как это отражает принцип социального государства, политика которого направлена на создание условий, обеспечивающих достойную жизнь и свободное развитие человека.
Ответ: 456.
Продолжаем решать задачи на теорию игр. Сегодня у нас разбор 20 задания из ЕГЭ по информатике 2021.
Задача (Одна куча)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 65. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 65 или больше камней. В начальный момент в куче было S камней 1 ≤ S ≤ 64.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Решение:
Ⅰ. Ход Пети.
S0 — первоначальное количество камней в куче.
Т.к. Петя не может выиграть на своём своём первом ходе, то найдём значения S0, при которых это возможно.
Распишем все варианты для Петиного первого хода.
| +1 | *2 |
| S0+1 < 65 S0 < 64 |
2*S0 < 65 S0 < 33 (Округляем в большую сторону) |
Все случаи должны быть удовлетворены, поэтому наш ответ должен быть меньше 33.
S0 < 33
ⅠⅠ. Ход Вани.
Рассмотрим все два случая:
1. S0+1 (Петя сделал +1 к кучке)
Ваня ни при каких обстоятельствах не должен выиграть на своём первом ходе. Найдём при каких значениях S0 это будет выполняться для этой ветки.
| +1 | *2 |
| S0 + 2 < 65 S0 < 63 |
2*S0 + 2 < 65 2*S0 < 63 S0 < 32 (Округляем в большую сторону) |
Для случая, когда Петя сделал +1 к кучке на первом своём ходу получается ограничение:
S0 < 32
Рассмотрим, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил кучку: S0+1+1 = S0+2
| +1 | *2 |
| S0 + 3 ≥ 65 S0 ≥ 62 |
2*S0 + 4 ≥ 65 2*S0 ≥ 61 S0 ≥ 31 (Округляем в большую сторону) |
С учётом всех ограничений получили значение S0 = 31, при котором Петя может выиграть на втором своём ходе.
б) Ваня оставил кучку: 2*(S0+1) = 2*S0 + 2
| +1 | *2 |
| 2*S0 + 3 ≥ 65 2 * S0 ≥ 62 S0 ≥ 31 |
4*S0 + 4 ≥ 65 4*S0 ≥ 61 S0 ≥ 16 (Округляем в большую сторону) |
Проанализируем два варианта a) и б) и понимаем, что в ответ пойдёт S0 = 31. При таком начальном количестве камней у Вани не будет возможности «испортить игру» и в случае а), и в случае б).
2. 2*S0 (Петя удвоил количество камней в куче.)
Найдём ограничения, при которых Ваня не выиграет при любых условиях на своём первом ходе.
| +1 | *2 |
| 2*S0 + 1 < 65 2*S0 < 64 S0 < 32 |
4*S0 < 65 S0 < 17 (Округляем в большую сторону) |
Значит, при этом первом ходе Пети, S0 должно быть меньше 17.
S0 < 17
Узнаем, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил 2*S0+1.
| +1 | *2 |
| 2*S0 + 2 ≥ 65 2*S0 ≥ 63 S0 ≥ 32 (Округляем в большую сторону) |
4*S0 + 2 ≥ 65 4*S0 ≥ 63 S0 ≥ 16 (Округляем в большую сторону) |
С учётом ограничения S0 < 17 получаем значение S0 = 16.
б) Ваня оставил 2*2*S0 = 4*S0.
| +1 | *2 |
| 4*S0 + 1 ≥ 65 4*S0 ≥ 64 S0 ≥ 16 |
8*S0 ≥ 65 S0 ≥ 9 (Округляем в большую сторону) |
Объединив a) и б) для второго случая (когда первый ход Пети был 2*S0), получаем значение S0 = 16. Мы проверяли пункт б), чтобы проверить, нет ли возможности у Вани «испортить» игру.
В задаче просили найти 2 значения для переменной S, при которых будут выполняться условия задачи. Мы нашли два значения. На этом можно завершить решение и записать ответ.
Ответ: 1631
Решим задачу из Демонстрационного варианта ЕГЭ по информатике 2021.
Задача (Демонстрационный вариант ЕГЭ по информатике 2021)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы,
у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было семь камней, во второй куче –
S камней; 1 ≤ S ≤ 69.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Найдите два таких значения S,
при которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как
будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение:
Обозначим первую кучу за a, вторую кучу за b.
Ⅰ. Ход Пети.
S0 — первоначальное количество камней во второй куче.
a=7, b=S0.
Т.к. Петя не может выиграть на своём своём первом ходе, то найдём значения S0, при которых это возможно.
Петя может сделать всего 4 действия. Распишем сумму двух кучек для 4-х случаев. Эти суммы должны быть меньше 77.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 8 < 77 S0 < 69 |
S0 + 8 < 77 S0 < 69 |
S0 + 14 < 77 S0 < 63 |
2*S0 + 7 < 77 2*S0 < 70 S0 < 35 |
Все случаи должны быть удовлетворены, поэтому наш ответ должен быть меньше 35.
S0 < 35
ⅠⅠ. Ход Вани.
Рассмотрим случай, когда Петя оставил следующие кучки:
1. a=8, b=S0 (Петя сделал +1 к первой кучке)
Ваня ни при каких обстоятельствах не должен выиграть на своём первом ходе. Найдём при каких значениях S0 это будет выполняться для этой ветки.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 9 < 77 S0 < 68 |
S0 + 9 < 77 S0 < 68 |
S0 + 16 < 77 S0 < 61 |
2*S0 + 8 < 77 2*S0 < 69 S0 < 35 (Округляем в большую сторону) |
Получается, что для случая, когда Петя сделал +1 к первой кучке, нам подходят значения для S0 < 35. В этом случае есть возможность Ване НЕ выиграть на своём ходе. Это ограничение совпадает с главным ограничением, которое мы получили на первом ходе Пети.
S0 < 35
Рассмотрим, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил a=9 (8+1), b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 10 ≥ 77 S0 ≥ 67 |
S0 + 10 ≥ 77 S0 ≥ 67 |
S0 + 18 ≥ 77 S0 ≥ 59 |
2*S0 + 9 ≥ 77 2*S0 ≥ 68 S0 ≥ 34 |
С учётом всех ограничений получили значение S0 = 34, при котором Петя будет выигрывать на втором своём ходе. Это значение наибольшее в допустимом диапазоне. Меньше значение теперь мы получить не можем (при данном первом ходе Пети), потому что у Вани есть возможность всегда «свернуть» в пункт а), и здесь значения меньшие, чем 34 не проходят.
Рассмотрим остальные ходы Вани. Если у него будет возможность пойти так, что Петя на втором ходе не сможет выиграть, значит, он так всегда сможет ходить, и наш ответ S0 = 34 нельзя будет засчитать.
б) Ваня оставил a=8, b=S0+1.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 10 ≥ 77 S0 ≥ 67 |
S0 + 10 ≥ 77 S0 ≥ 67 |
S0 + 17 ≥ 77 S0 ≥ 60 |
2*S0 + 10 ≥ 77 2*S0 ≥ 67 S0 ≥ 34 (Округляем в большую сторону) |
В пункте б) есть решение.
в) Ваня оставил a=16, b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 17 ≥ 77 S0 ≥ 60 |
S0 + 17 ≥ 77 S0 ≥ 60 |
S0 + 32 ≥ 77 S0 ≥ 45 |
2*S0 + 16 ≥ 77 2*S0 ≥ 61 S0 ≥ 31 (Округляем в большую сторону) |
В пункте в) есть решения.
г) Ваня оставил a=8, b=2*S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| 2*S0 + 9 ≥ 77 2*S0 ≥ 68 S0 ≥ 34 |
— | — | — |
Пункт г) тоже имеет решение. Как только нашли за Петю решение, можно прекратить рассматривать оставшиеся ходы у Пети на втором ходе, потому что мы нашли уже максимальное значение S0 = 34 из диапазона S0 < 35, и в пунктах б), в), г) нам важно убедиться, что решения просто есть.
Мы должны выбрать из всех четырёх пунктов (а), б), в), г)) самое больше число. Это будет S0 = 34. Именно это значение удовлетворяет всем четырём пунктам одновременно. Тогда у Вани не будет возможности сходить так, что Петя на своём втором ходе не сможет выиграть.
Получается, что значение S0 = 34 пойдёт в ответ.
2. a=7, b=S0+1 (Петя сделал +1 ко второй кучке)
Найдём ограничения, при которых Ваня не выиграет при любых условиях на своём первом ходе.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 9 < 77 S0 < 68 |
S0 + 9 < 77 S0 < 68 |
S0 + 15 < 77 S0 < 62 |
2*S0 + 9 < 77 2*S0 < 68 S0 < 34 |
Значит, при этом первом ходе Пети, S0 должно быть меньше 34.
S0 < 34
Узнаем, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил a=8 (7+1), b=S0+1.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 10 ≥ 77 S0 ≥ 67 |
S0 + 10 ≥ 77 S0 ≥ 67 |
S0 + 17 ≥ 77 S0 ≥ 60 |
2*S0 + 10 ≥ 77 2*S0 ≥ 67 S0 ≥ 34 (Округляем в большую сторону) |
Видим, что у Вани есть возможность «свернуть» на путь a=8 (7+1), b=S0+1, и тем самым, не оставить шансов Пети выиграть. (Ни одно неравенство не пройдёт ограничение S0 < 34).
Значит, вариант a=7, b=S0+1 на первом Петином ходу не принёс результатов.
3. a=14, b=S0 (Петя увеличил первую кучку в 2 раза.)
Найдём ограничения, при которых Ваня не выиграет при любых условиях на своём первом ходе.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 15 < 77 S0 < 62 |
S0 + 15 < 77 S0 < 62 |
S0 + 28 < 77 S0 < 49 |
2*S0 + 14 < 77 2*S0 < 63 S0 < 32 (Округляем в большую сторону) |
Значит, при этом первом ходе Пети, S0 должно быть меньше 32.
S0 < 32
Узнаем, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил a=15 (14+1), b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 16 ≥ 77 S0 ≥ 61 |
S0 + 16 ≥ 77 S0 ≥ 61 |
S0 + 30 ≥ 77 S0 ≥ 47 |
2*S0 + 15 ≥ 77 2*S0 ≥ 62 S0 ≥ 31 |
С учётом ограничения S0 < 32 получаем значение S0 = 31. Получили наибольшее значение в допустимом диапазоне. Значит, меньше чем 31, в данной ветке значение быть не может.
Убедимся, что при остальных ходах Вани, Петя сможет выиграть на своём втором ходе.
б) Ваня оставил a=14, b=S0+1.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 16 ≥ 77 S0 ≥ 61 |
S0 + 16 ≥ 77 S0 ≥ 61 |
S0 + 29 ≥ 77 S0 ≥ 48 |
2*S0 + 16 ≥ 77 2*S0 ≥ 61 S0 ≥ 31 (Округляем в большую сторону) |
Пункт б) имеет решение.
в) Ваня оставил a=28, b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 29 ≥ 77 S0 ≥ 48 |
S0 + 29 ≥ 77 S0 ≥ 48 |
S0 + 56 ≥ 77 S0 ≥ 21 |
— |
Пункт в) имеет решения.
г) Ваня оставил a=14, b=2*S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| 2*S0 + 15 ≥ 77 2*S0 ≥ 62 S0 ≥ 31 |
— | — | — |
В пункте г) есть решение.
Таким образом, мы нашли наибольшее решение S0 = 31 при ограничении S0 < 32. Оно подходит для всех четырёх пунктов а), б) в), г).
В задаче просили найти 2 значения для переменной S, при которых будут выполняться условия задачи. Мы нашли два значения. На этом можно завершить решение и записать ответ.
Ответ: 3134
Посмотрим ещё одну задачу 20 Задания из примерных вариантов ЕГЭ по информатике 2021.
Задача (Закрепление)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в одну из куч один камень или
увеличить количество камней в куче в два раза.
Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (12, 9), (6, 10), (6, 18). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 74. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 74 или больше камней.
В начальный момент в первой куче было 12 камней, во второй куче — S камней, 1 ≤ S ≤ 61.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т. е не гарантирующие выигрыш независимо от игры противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Решение:
Обозначим первую кучу за a, вторую кучу за b.
Ⅰ. Ход Пети.
S0 — первоначальное количество камней во второй куче.
a=12, b=S0.
Т.к. Петя не может выиграть на своём своём первом ходе, то найдём значения S0, при которых это возможно.
Петя может сделать всего 4 действия. Распишем сумму двух кучек для 4-х случаев. Эти суммы должны быть меньше 74.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 13 < 74 S0 < 61 |
S0 + 13 < 74 S0 < 61 |
S0 + 24 < 74 S0 < 50 |
2*S0 + 12 < 74 2*S0 < 62 S0 < 31 |
Все случаи должны быть удовлетворены, поэтому наш ответ должен быть меньше 31.
S0 < 31
ⅠⅠ. Ход Вани.
Рассмотрим случай, когда Петя оставил следующие кучки:
1. a=13, b=S0 (Петя сделал +1 к первой кучке)
Ваня ни при каких обстоятельствах не должен выиграть на своём первом ходе. Найдём при каких значениях S0 это будет выполняться для этой ветки.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 14 < 74 S0 < 60 |
S0 + 14 < 74 S0 < 60 |
S0 + 26 < 74 S0 < 48 |
2*S0 + 13 < 74 2*S0 < 61 S0 < 31 (Округляем в большую сторону) |
Получается, что для случая, когда Петя сделал +1 к первой кучке, нам подходят значения для S0 < 31. В этом случае есть возможность Ване НЕ выиграть на первом своём ходе. Это ограничение совпадает с главным ограничением, которое мы получили на первом ходе Пети.
S0 < 31
Рассмотрим, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил a=14 (13+1), b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 15 ≥ 74 S0 ≥ 59 |
S0 + 15 ≥ 74 S0 ≥ 59 |
S0 + 28 ≥ 74 S0 ≥ 46 |
2*S0 + 14 ≥ 74 2*S0 ≥ 60 S0 ≥ 30 |
С учётом всех ограничений получили значение S0 = 30, при котором Петя будет выигрывать на втором своём ходе. Это максимальное значение, для данного ограничения S0 < 32. Даже, если мы найдём меньшее число при других ходах Вани в этой ветке, всё равно мы выберем значение 32. Но всё же нужно проверить остальные ходы Вани, вдруг у него будет возможность выводить нас на такую ситуацию, когда Петя не сможет выиграть на своём втором ходе.
б) Ваня оставил a=13, b=S0+1.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 15 ≥ 74 S0 ≥ 59 |
S0 + 15 ≥ 74 S0 ≥ 59 |
S0 + 27 ≥ 74 S0 ≥ 47 |
2*S0 + 15 ≥ 74 2*S0 ≥ 59 S0 ≥ 30 (Округляем в большую сторону) |
Пункт б) имеет решения.
в) Ваня оставил a=26, b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 27 ≥ 74 S0 ≥ 47 |
S0 + 27 ≥ 74 S0 ≥ 47 |
S0 + 52 ≥ 74 S0 ≥ 22 |
— |
Пункт в) имеет решения.
г) Ваня оставил a=13, b=2*S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| 2*S0 + 14 ≥ 74 2*S0 ≥ 60 S0 ≥ 30 |
— | — | — |
Пункт г) имеет решение.
Таким образом, значение S0 = 30 удовлетворяет всем четырём пунктам, и у Вани нет возможности «испортить праздник» Пети.
Один ответ есть.
2. a=12, b=S0+1 (Петя сделал +1 ко второй кучке)
Найдём ограничения, при которых Ваня не выиграет при любых условиях на своём первом ходе.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 14 < 74 S0 < 60 |
S0 + 14 < 74 S0 < 60 |
S0 + 25 < 74 S0 < 49 |
2*S0 + 14 < 74 2*S0 < 60 S0 < 30 |
Значит, при этом первом ходе Пети, S0 должно быть меньше 30.
S0 < 30
Узнаем, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил a=13 (12+1), b=S0+1.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 15 ≥ 74 S0 ≥ 59 |
S0 + 15 ≥ 74 S0 ≥ 59 |
S0 + 27 ≥ 74 S0 ≥ 47 |
2*S0 + 15 ≥ 74 2*S0 ≥ 67 S0 ≥ 30 (Округляем в большую сторону) |
Видим, что у Вани есть возможность «свернуть» на путь a=13 (12+1), b=S0+1, и тем самым, не оставить шансов Пети выиграть. (Ни одно неравенство не пройдёт ограничение S0 < 30).
Значит, вариант a=12, b=S0+1 на первом Петином ходу не принёс результатов.
3. a=24, b=S0 (Петя увеличил первую кучку в 2 раза.)
Найдём ограничения, при которых Ваня не выиграет при любых условиях на своём первом ходе.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 25 < 74 S0 < 49 |
S0 + 25 < 74 S0 < 49 |
S0 + 48 < 74 S0 < 26 |
2*S0 + 24 < 74 2*S0 < 50 S0 < 25 |
Значит, при этом первом ходе Пети, S0 должно быть меньше 25.
S0 < 25
Узнаем, при каких значениях S0 Петя на втором своём ходе может выиграть в данной ситуации.
a) Ваня оставил a=25 (24+1), b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 26 ≥ 74 S0 ≥ 48 |
S0 + 26 ≥ 74 S0 ≥ 48 |
S0 + 50 ≥ 74 S0 ≥ 24 |
2*S0 + 27 ≥ 74 2*S0 ≥ 47 S0 ≥ 24 (Округляем в большую сторону) |
С учётом ограничения S0 < 25 получаем значение S0 = 24. Максимальное значение при допустимом диапазоне. Значит, меньше чем 24, значение при данном первом ходе Пети быть не может, иначе оно не будет проходить в пункте а).
Проверим остальные ходы Вани.
б) Ваня оставил a=24, b=S0+1.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 26 ≥ 74 S0 ≥ 48 |
S0 + 26 ≥ 74 S0 ≥ 48 |
S0 + 49 ≥ 74 S0 ≥ 25 |
2*S0 + 26 ≥ 74 2*S0 ≥ 48 S0 ≥ 24 |
Пункт б) имеет решение.
в) Ваня оставил a=48, b=S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 49 ≥ 74 S0 ≥ 25 |
S0 + 49 ≥ 74 S0 ≥ 25 |
S0 + 96 ≥ 74 S0 ≥ 1 |
— |
Пункт в) имеет решения.
г) Ваня оставил a=24, b=2*S0.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| 2*S0 + 25 ≥ 74 2*S0 ≥ 49 S0 ≥ 25 |
2*S0 + 25 ≥ 74 2*S0 ≥ 49 S0 ≥ 25 |
2*S0 + 48 ≥ 74 2*S0 ≥ 26 S0 ≥ 13 |
— |
Пункт г) имеет решения.
Ваня не сможет сделать такой ход, при котором Петя не сможет выиграть на втором ходе.
Выбираем такое значение S0 = 24, которое подходит под все пункты а), б), в), г).
Пишем ответ из двух значений 24 и 30.
Ответ: 2430
На этом всё. Удачи на экзамене по информатике 2021!