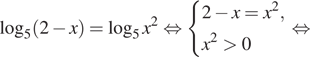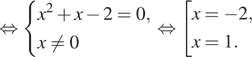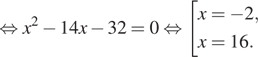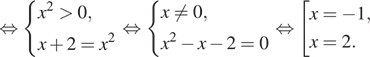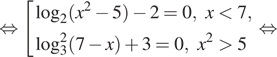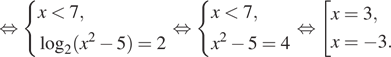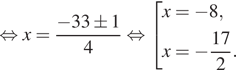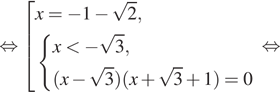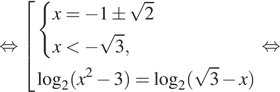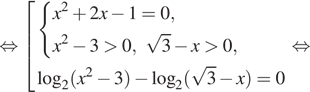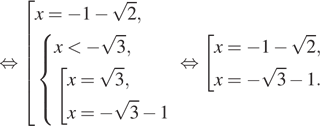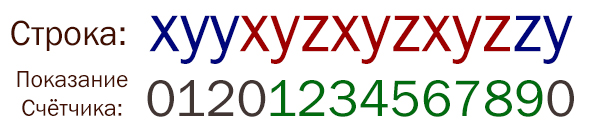Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Задания Д4 № 252611
Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 244983: 252611 252637 505375 505396 252613 252615 252617 252619 252621 252623 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Спрятать решение
Решение.
Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких квадратов и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Ответ: 3.
Примечание.
Наш четырёхугольник — ромб, его площадь равна половине произведения диагоналей. Поэтому она равна 3.
Свойства натурального числа 252611, 0x03DAC3, 0x3DAC3:
Рейтинг 0 из 10,
оценок: 0.
Системы счисления, перевод в систему счисления
Десятичное число 252611
-
- 252611 в шестнадцатеричной системе счисления
- 3DAC3
-
- 252611 в двоичной системе счисления
- 111101101011000011
-
- 252611 в восьмеричной системе счисления
- 755303
Шестнадцатеричное число 3DAC3
-
- 3DAC3 в десятичной системе
- 252611
-
- 3DAC3 в двоичной системе
- 111101101011000011
-
- 3DAC3 в восьмеричной системе
- 755303
Двоичное число 111101101011000011
-
- 111101101011000011 в десятичной системе
- 252611
-
- 111101101011000011 в шестнадцатеричной системе
- 3DAC3
-
- 111101101011000011 в восьмеричной системе
- 755303
Восьмеричное число 755303
-
- 755303 в десятичной системе
- 252611
-
- 755303 в шестнадцатеричной системе
- 3DAC3
-
- 755303 в двоичной системе
- 111101101011000011
Основные арифметические и алгебраические свойства
-
- Число 252611 на русском языке, number in Russian, число 252611 прописью:
- двести пятьдесят две тысячи шестьсот одиннадцать
-
- Четность
- Нечетное число 252611
-
- Разложение на множители, делители числа 252611
- 252611, 1
-
- Простое или составное число
- Простое число 252611
-
- Числа делящиеся на целое число 252611
- 505222, 757833, 1010444, 1263055, 1515666, 1768277, 2020888, 2273499
-
- Число 252611 умноженное на число два
- 505222
-
- 252611 деленное на число 2
- 126305.5
-
- Список 8-ми простых чисел перед числом
- 252607, 252589, 252583, 252559, 252541, 252533, 252509, 252481
-
- Сумма десятичных цифр
- 17
-
- Количество цифр
- 6
-
- Десятичный логарифм 252611
- 5.4024522580771
-
- Натуральный логарифм 252611
- 12.43960603506
-
- Это число Фибоначчи?
- Нет
-
- Число на 1 больше числа 252611,
следующее число - число 252612
- Число на 1 больше числа 252611,
-
- Число на 1 меньше числа 252611,
предыдущее число - 252610
- Число на 1 меньше числа 252611,
Степени числа, корни
-
- 252611 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 63812317321
- 252611 во второй степени (в квадрате)
-
- В третьей степени (в кубе, 252611 в степени 3, x³) равно
- 16119693290775131
-
- Корень квадратный из 252611
- 502.60421804836
-
- Корень кубический из числа 252611 =
- 63.214603659393
Тригонометрические функции, тригонометрия
-
- Синус, sin 252611 градуса, sin 252611°
- -0.9455185756
-
- Косинус, cos 252611 градуса, cos 252611°
- -0.3255681545
-
- Тангенс, tg 252611 градуса, tg 252611°
- 2.9042108777
-
- Синус, sin 252611 радиан
- 0.969622436294
-
- Косинус, cos 252611 радиан
- -0.2446064819977
-
- Тангенс, tg 252611 радиан равно
- -3.9640095731524
-
- 252611 градус, 252611° =
- 4408.8936767554 радиан
-
- 252611 радиан =
- 14473544.158579 градуса, 14473544.158579°
Контрольные суммы, хэши, криптография
-
- MD-5 хэш(252611)
- 3e9e916d7494d788bdea0184540082fd
-
- CRC-32, CRC32(252611)
- 2096537203
-
- SHA-256 hash, SHA256(252611)
- 80a6ea715c585112a82903d07bc2218290d7fb719d207d2a06b0a8c5d1a41ab9
-
- SHA1, SHA-1(252611)
- 638a8dbf377740db81b7f56534a970b9024b4471
-
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(252611)
- 5551a0ab83a22801b85d1d1e75ee2276f707051b09ed8d15690a96e94823ca18
-
- Base64
- MjUyNjEx
Языки программирования
-
- C++, CPP, C значение 252611
- 0x03DAC3, 0x3DAC3
-
- Delphi, Pascal значение числа 252611
- $03DAC3
Дата и время
-
- Конвертация UNIX timestamp 252611 в дату и время
-
- UTC
- суббота, 3 января 1970 г., 22:10:11 GMT
- в Москве, Россия
- воскресенье, 4 января 1970 г., 1:10:11 Московское стандартное время
- в Лондоне, Великобритания
- суббота, 3 января 1970 г., 23:10:11 GMT+01:00
- в Нью-Йорке, США
- суббота, 3 января 1970 г., 17:10:11 Восточно-американское стандартное время
Интернет
-
- Конвертация в IPv4 адрес Интернет
- 0.3.218.195
-
- 252611 в Википедии:
- 252611
Другие свойства числа
-
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/252611
-
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x3DAC3
-
- Номер телефона
- 25-26-11
-
- html RGB цвет 252611, 16-ричное значение
- #03DAC3 — (3, 218, 195)
-
- HTML CSS код цвета #03DAC3
- .color-mn { color: #03DAC3; }
.color-bg { background-color: #03DAC3; }
Цвет для данного числа 252611
Здесь вы можете изменить составляющую цвета для данного числа 252611 или цвета 03DAC3:
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
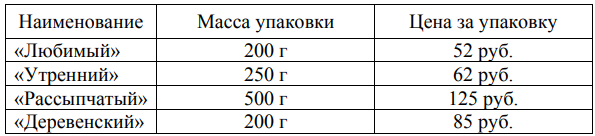
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
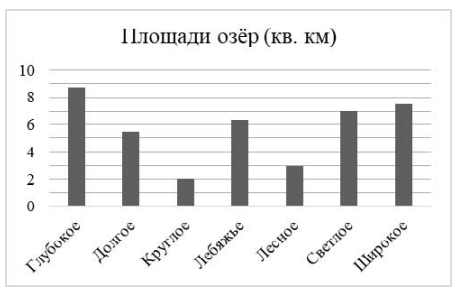
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
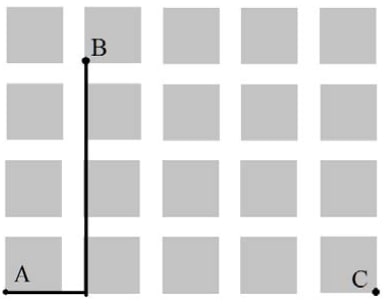
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
На экранах долгожданный шестой сезон одного из самых популярных и востребованных сериалов на зарубежном телевидении. Проект «Викинги» повествует о выдающемся воинственном народе, который проживает в Скандинавии и управляется безумным, яростным, но при этом очень мудрым правителем Рагнаром Лодброком. Этот человек смог собрать вокруг себя верных людей, смог установить свои правила на родных территориях, а вскоре отправился на покорение европейских земель. Главный герой повёл за собой свою армию, которая дошла с ним до территории Франции, осадив Париж и забрав сокровища одной из самых могущественных стран центральной Европы! Викингам по силам оказалось разбить армии англичан, которых не спасло даже нахождение на море. Ко всему прочему, главные персонажи сумели пробиться вглубь континента, наворотив дел и в других частях Европы.Продолжение истории обещает зрителям ещё более интересные походы. В этот раз главный герой вместе с верными товарищами отправится на восточные земли. Его встреча с Вещим Олегом, роль которого исполнит великолепный российский актёр Данила Козловский будет судьбоносной. Но чем же обернётся новый сезон знаменитого сериала?
- Название: Vikings
- Год выхода: 2013-03-03
- Страна: Канада, Ирландия
- Режиссер: Киаран Доннелли, Кен Джиротти, Стивен Ст.
- Статус сериала: Завершен
- Перевод: LostFilm
- Качество: FHD (1080p) (45 мин)
- Возраст: Сериал для зрителей старше 18+ лет
-
8.2
8.5
- В главных ролях: Кэтрин Уинник, Густаф Скарсгард, Александр Людвиг, Джорджия Хёрст, Алекс Хег Андерсен, Джордан Патрик Смит, Марко Ильсё, Петер Францен, Трэвис Фиммел, Клайв Стэнден
- Жанры: Приключения, Военный, Исторический, Боевик, Мелодрама, Драма
6 сезон 21 серия
Викинги смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет
К сожалению некоторые диалоги в сериале не переведены, рекомендуем в настройках включить субтитры, чтобы понимать диалоги. Приятного просмотра!
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Положительное вещественное
шестизначное
число 525142
является составным.
19 — сумма всех цифр данного числа.
У числа 525142 8 делителей.
И сумма этих делителей: 793800.
525142 и 0.0000019042468513278313 являются взаимно обратными числами.
Число в других системах счисления:
двоичная система: 10000000001101010110, троичная система: 222200100201, восьмеричная система: 2001526, шестнадцатеричная система: 80356.
512 килобайтов 854 байта — столько информации находится в числе байт 525142.
Число 525142 в виде кода азбуки Морзе: ….. ..— ….. .—- ….- ..—
Число — не число Фибоначчи.
Косинус числа: 0.9411, синус числа: -0.3380, тангенс числа: -0.3591.
Натуральный логарифм числа: 13.1714.
Число имеет десятичный логарифм: 5.7203.
724.6668 — корень квадратный, 80.6787 — корень кубический.
Возведение числа в квадрат: 2.7577e+11.
525142 в секундах это 6 дней 1 час 52 минуты 22 секунды .
Нумерологическое цифра числа 525142 — 1.
На чтение 1 мин Просмотров 26 Опубликовано 5 марта, 2023
Тригонометрические уравнения решу ЕГЭ 2022 профиль с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Задание №1 ЕГЭ 2022 профильный уровень тригонометрические уравнения 6 задач решу ЕГЭ с ответами и решением для подготовки, решаем примеры
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%82%d1%80%d0%b8%d0%b3%d0%be%d0%bd%d0%be%d0%bc%d0%b5%d1%82%d1%80%d0%b8%d1%87%d0%b5%d1%81%d0%ba%d0%b8%d0%b5-%d1%83%d1%80%d0%b0%d0%b2%d0%bd%d0%b5%d0%bd%d0%b8%d1%8f-%d1%80%d0%b5%d1%88%d1%83-%d0%b5/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.

2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Логарифмические
уравнения из материалов ЕГЭ профильного уровня.
(Для
всех уравнений делается проверка или находится ОДЗ).
1. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. а) Запишем
исходное уравнение в виде:
б) Поскольку отрезку
принадлежит
единственный корень −2.
Ответ: а) −2; 1, б) −2.
2. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. а) Из
уравнения получаем:
б) Заметим, что Значит,
указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие
отрезку
Решение. а) Запишем
исходное уравнение в виде:
Значит, откуда
или
откуда
б) Заметим, что
Значит, указанному отрезку принадлежит корень 2.
Ответ: а) 2 и б) 2.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие
отрезку
Решение. а) Заметим,
что уравнение определено при любом Запишем исходное уравнение
в виде:
Значит, либо откуда
или
либо
откуда
или
б) Поскольку отрезку
принадлежат
корни и
Ответ: а) б)
5. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие
отрезку
Решение. а) Поскольку
получаем:
б) В силу цепочки соотношений заданному
отрезку принадлежит только число −1.
Ответ: а) {−1, 2}, б) −1.
6. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
промежутку
Решение. а) Преобразуем
уравнение:
б) Заметим, что
поэтому в указанный промежуток попадает только корень
Ответ: а) {−3; 3} б) 3.
7. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. а) Заметим,
что уравнение имеет смысл при (⁎). Преобразуем его при
этих условиях:
б) Заметим, что 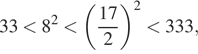
подходят оба корня.
Ответ: а) б)
8. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие
отрезку [−2,5; −1,5].
Решение. а) Запишем
исходное уравнение в виде:
б) Проверим корни на отрезке :
Поскольку конечное неравенство верное, значение подходит и войдет в ответ.
Проверим следующее значение x:
Так как второе значение не дает правильного конечного неравенства, оно
не войдет в ответ.
Ответ: а) б)
Скачано с www.znanio.ru
Сегодня посмотрим одно из самых интересных заданий из ЕГЭ по информатике 2023. Будем решать 24 задание. В этом задании нужно работать с файлами.
Все решения задач из задания 24 ЕГЭ по информатике 2023 будут приведены на языке программирования Python (Питон).
Поехали!
Задача (Самая простая)
Текстовый файл состоит не более чем из 106 символов A, B и C. Определите максимальное количество идущих подряд символов B. Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Решение:
Решим данную задачу на языке Python.
f=open('24_1.txt') s=f.read() k=0 kmax=0 for i in range(0, len(s)): if s[i]=='B': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax)
С помощью команды open() подвязываемся к файлу. Чтобы не прописывать полный путь, файл должен лежать в той же папке, что и программа.
С помощью команды .read() зачитываем в переменную s всё содержимое файла.
Переменная k — это текущий счётчик символов «B». Задача переменной kmax сохранить максимальное значение k.
С помощью цикла for перебираем все символы из строки s. Переменная i пробегается по номерам всех симолов. Счёт символов начинается в строке с нуля. В начале берём нулевой символ, потом первый и т.д. Конструкция for i in range(0, len(s)) позволяет пройтись по всем символам строки до конца.
Если нам встретился нужный символ «B», то мы счётчик прибавляем на 1. Это значит, что мы подсчитываем текущую цепочку. Если будет стоять 3 символа «B» подряд, значит, счёт k покажет значение 3. Как только встретится дургой символ, то это означает, что цепочка прервалась и счётчик переводится в первоначальное положение 0.
При любом увеличении счётчика происходит анализ этого счётчика на максимальность. Функция max выбирает максимальное значение из старого значения kmax и нового показания счётчика k. Если счётчику k удалось победить kmax, то его значение будет считаться максимальным на данный момент времени.
В ответ идёт значение kmax. Это и есть длина максимальной цепочки. В этой задачке ответ получается 11.
Ответ: 11
Закрепим это простое задание из ЕГЭ по информатике 2023.
Задача (Простая, закрепление)
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых нет символа Z. Для выполнения этого задания следует написать программу.
Решение:
Решение похоже на предыдущее.
f=open('24_2.txt') s=f.read() k=0 kmax=0 for i in range(0, len(s)): if s[i]!='Z': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax)
Если нет символов «Z», то подсчитываем, иначе сбрасываем.
Задача (Обращаемся к соседу)
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальное количество идущих подряд символов, расположенных в алфавитном порядке (возможно с повторением симолов). Для выполнения этого задания следует написать программу.
Решение:
f=open('24_2.txt') s=f.read() k=1 kmax=0 for i in range(0, len(s)-1): if s[i]<=s[i+1]: k=k+1 kmax=max(k, kmax) else: k=1 print(kmax)
В ответе получается 15. Символы можно сравнивать между собой с помощью знаков «>» или меньше «<» ( а так же «>=» или «<=»), причём это сравнение происходит в алфавитном порядке. Например, символ «B» будет больше, чем «A» и т.п. Теперь нам нужно уже обратится к соседу, уже важна связь между соседними символами. Раз мы обращаемся к следующему символу, то должны пробегать до len(s)-1, иначе куда мы будем обращаться, когда дойдём до последнего символа?
В самом начале цепочки мы анализируем два символа, а к счётчику прибавляем всего лишь 1. Чтобы это учесть, в начале счётчику (переменной k) присваиваем 1. Затем, по мере продвижения по цепочке, мы добавляем в наш анализ 1 новый символ, и к счётчику добавляется одна 1. Дальше уже таких проблем нет.
Раз мы присвоили в переменную k единицу, то и сбрасывать в ветке else мы тоже должны на 1. Эти значения обычно взаимосвязаны.
Если мы обращаемся к соседнему символу, как правило, счётчик и сброс устанавливаются в 1. Это не стопроцентная истина, но иметь ввиду это нужно.
Ответ: 15
Задача (Обращаемся к соседу, закрепление)
Текстовый файл состоит не более чем из 106 символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд цифр, среди которых каждые две соседние различны. Для выполнения этого задания следует написать программу.
Решение:
f=open('24_3.txt') s=f.read() k=1 kmax=0 for i in range(0, len(s)-1): if s[i]!=s[i+1]: k=k+1 kmax=max(k, kmax) else: k=1 print(kmax)
Если соседи различны, мы подсчитываем, иначе сбрасываем.
Ответ: 120
Задача (Обращаемся к соседу, ещё сложнее)
Текстовый файл состоит не более чем из 106 символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд нечётных цифр, расположенных в неубывающем порядке. Для выполнения этого задания следует написать программу.
Решение:
f=open('24_3.txt') s=f.read() k=1 kmax=0 for i in range(0, len(s)-1): if s[i]<=s[i+1] and s[i] in '13579' and s[i+1] in '13579' : k=k+1 kmax=max(k, kmax) else: k=1 print(kmax)
Здесь опять можно применить знаки сравнения прям к символам. Удобно проверить принадлежность к нечётным цифрам конструкцией s[i] in ‘13579’. Нечётной цифрой должна быть как текущая, так и следующая.
Ответ: 8
Решим ещё одну тренировочную задачу из ЕГЭ по информатике 2023.
Задача (Обращаемся к соседу, ещё сложнее, закрепление)
Текстовый файл состоит не более чем из 106 символов 1, 2, 3, A, B, С. Определите максимальное количество идущих подряд символов, среди которых никакие две буквы и никакие две цифры не стоят рядом. Для выполнения этого задания следует написать программу.
Решение:
f=open('24_4.txt') s=f.read() k=1 kmax=0 for i in range(0, len(s)-1): if (s[i] in '123' and s[i+1] in 'ABC') or (s[i] in 'ABC' and s[i+1] in '123') : k=k+1 kmax=max(k, kmax) else: k=1 print(kmax)
В этой задаче цифры и буквы должны чередоваться. Если у нас цифра, то следующая должны быть буква, или наоборот, если у нас буква, то следующая должна быть цифра. В этих двух случаях прибавляем к счётчику 1.
Ответ: 20
Задача (Исключаем строку из 2-х символов, демо 2022)
Текстовый файл состоит из символов P, Q, R и S.
Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет идущих подряд символов P.
Для выполнения этого задания следует написать программу.
Решение:
Напишем решение на языке Python.
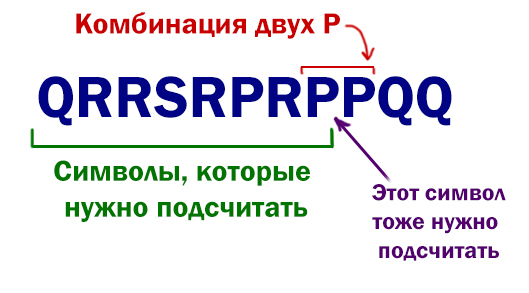
f=open('24_5.txt') s=f.read() k=1 kmax=0 for i in range(0, len(s)-1): if s[i]=='P' and s[i+1]=='P': k=1 else: k=k+1 kmax = max(k, kmax) print(kmax)
Подсчитываем символы, пока не встретилась комбинация двух P подряд. Как только встретилась данная комбинация, сбрасываем счётчик на 1. Здесь мы сбрасываем счётчик на значение 1, чтобы учесть один символ, которые находится в самой комбинации PP. И в начале мы тоже устанавливаем счётчик в значение 1 по этой же причине.
Мы проходим в цикле for до длины строки минус один. Значение 1 в счётчике при сбросе и в начале программы так же компенсирует и тот момент, что мы не подсчитываем последний символ!
При изменении счётчика, сохраняем максимальное значение в переменной mx
Если бы у нас была вместо PP другая комбинация, состоящая к примеру из 5 символов, то мы бы тогда в начале и при сбросе писали в счётчик значение 5-1=4.
Здесь тоже работает негласное правило, обращаемся к соседу, значит, счётчик устанавливаем в 1.
В этой задаче получается ответ 188.
Ответ: 188
Задача (Исключаем подстроку из 3-х символов)
Текстовый файл состоит из символов арабских цифр(0, 1, …,9).
Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет трёх символов 0, стоящих рядом.
Для выполнения этого задания следует написать программу.
Решение:
Напишем решение на языке Python.
f=open('24_6.txt') s=f.read() k=2 kmax=0 for i in range(0, len(s)-2): if s[i]=='0' and s[i+1]=='0' and s[i+2]=='0': k=2 else: k=k+1 kmax = max(k, kmax) print(kmax)
Чтобы понять это решение, нужно посмотреть предыдущую задачу. Мы здесь обращаемся к двум соседям, значит, счётчик устанавливаем в 2. Так же проходим в цикле до len(s)-2. Нежелательная строка может состоять не только из одинаковых символов. Может быть строка «XYYZ», к примеру.
Ответ: 7684
Задача (Не более одного символа Z)
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более одного раза.
Решение:
В нашей цепочке один раз можно встретиь символ Z, а два раза уже нельзя. Здесь мы применим функцию .split(). Как работает эта фнкция? Напишем тестовую программу.
s='sadqttqtreq' a=s.split('q') print(a)
Результат данной программы будет следующим:
[‘sad’, ‘tt’, ‘tre’, »]
Команда split «разрезает» строку по символу «q». В результате мы получаем массив с кусочками этой строки.
Решение нашей задачи.
f=open('24_7.txt') s=f.read() a=s.split('Z') k=0 kmax=0 for i in range(0, len(a)-1): k = len(a[i]) + 1 + len(a[i+1]) kmax = max(k, kmax) print(kmax)
Разрезаем нашу строку по символу «Z». Пробегаемся уже по массиву a. Цепочка-кандидат это текущий кусочек (a[i]), символ Z (1) и следующий кусочек (a[i+1]).
Каждого кандитата проверяем сразу на максимальность.
Ответ: 43
Задача (Не более двух символов Z)
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более двух раз.
Решение:
Решение аналогично предыдущему.
f=open('24_7.txt') s=f.read() a=s.split('Z') k=0 kmax=0 for i in range(0, len(a)-2): k = len(a[i]) + 1 + len(a[i+1]) + 1 + len(a[i+2]) kmax = max(k, kmax) print(kmax)
Ответ: 50
Задача (Звенья)
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальную длину цепочки символов, состоящей из повторяющихся фрагментов XYZ. Цепочка должна начинаться с символа X и заканчиваться символом Z. Например, для строки ZZZXYZXYZXZZZ длина цепочки равна 6: XYZ+XYZ
Решение:
Если мы подсчитаем количество идущих подряд звеньев XYZ, то, можно сказать, дело сделано.
f=open('24_8.txt') s=f.read() s=s.replace('XYZ', '1') k=0 kmax=0 for i in range(0, len(s)): if s[i]=='1': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax*3)
Мы с помощью команды replace заменили звенья на «1» (на символ, которого точно нет в файле). Теперь задача свелась к самой простой, которую мы рассматривали в начале статьи. Нужно просто подсчитать количество идущих поряд единиц.
В ответе нас просили указать количество символов, а не звеньев, поэтому переменную kmax умножаем на 3.
Ответ: 66
Задача (Звенья, закрепление)
Текстовый файл состоит не более, чем из 106 символов из набора A, B, С. Найдите максимальное количество идущих пар символов AC или AB. Искомая подстрока может включать только пары AB, только пары AC или содержать одновременно как пары AC, так и пары AB.
Решение:
f=open('24_9.txt') s=f.read() s=s.replace('AB', '1') s=s.replace('AC', '1') k=0 kmax=0 for i in range(0, len(s)): if s[i]=='1': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax)
Здесь нам подходит звено, как и AB, так и AC. В ответе нужно указать количество пар, поэтому не на что умножать переменную kmax не нужно.
Ответ: 19
Задача (Звенья, основная волна 20.06.22)
Текстовый файл состоит из символов A, B, C, D и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполенения этого задания следует написать программу.
Решение:
f=open('24_10.txt') s=f.read() s=s.replace('BA', '1') s=s.replace('CA', '1') s=s.replace('DA', '1') s=s.replace('BO', '1') s=s.replace('CO', '1') s=s.replace('DO', '1') k=0 kmax=0 for i in range(0, len(s)): if s[i]=='1': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax)
Ответ: 174
Задача (Звенья, последнее звено неполное)
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальную длину цепочки вида XYZXYZXYZ… (составленной из фрагментов XYZ, последний фрагмент может быть неполным). Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Решение:
Т.к. последнее звено может быть неполным, здесь удобно применить другой алгоритм.
Пусть в начале показания счётчика равно нулю. Если мы находим нужный нам символ в нужной последовательности, то прибавляем к счётчику 1. Если последовательность сбивается, то ставим счётчик в ноль.
На рисунке представлен данный алгоритм. В нижней строке указано показание счётчика в момент анализа символа.
На данном рисунке максимальная длина цепочки нужных символов равна 9.
Видим, что для символа X, когда он находится на своём месте, остаток от деления значения счётчика на 3 равен 0.
Для символа Y, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 1.
Для символа Z, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 2.
Мы смотрим остаток от деления на 3, потому что у нас длина звена равна трём (XYZ).
Таким образом, мы и наш анализ очередного символа привяжем к показанию счётчика:
f=open('24_11.txt') s=f.read() k=0 kmax=0 for i in range(0, len(s)): if (s[i]=='X' and k%3==0) or (s[i]=='Y' and k%3==1) or (s[i]=='Z' and k%3==2): k=k+1 kmax = max(k, kmax) else: if s[i]=='X': k=1 else: k=0 print(kmax)
Важный момент: Если нужную цепочку прервал символ X, то нужно счётчик сразу выставить в 1, иначе может произойти такая ошибка:
Т.е. первые три нужных символа в цепочке алгоритм не засчитал.
Поэтому мы не просто сбрасываем счётчик в ноль, а прописываем условие:
if s[i]=='X': k=1 else: k=0
Ответ: 13
Задача (Полезный приём)
Текстовый файл 24-157.txt состоит не более чем из 106 символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле между двумя одинаковыми символами. Например, в тексте CCBAABABCBC есть комбинации ABA, BAB, BCB и CBC. Чаще всего – 2 раза – между двумя одинаковыми символами стоит B, в ответе для этого случая надо написать B2 (без пробелов и других разделителей). Если таких символов несколько, выведите тот, который стоит раньше в алфавите.
Решение:
f=open('24-157.txt') s=f.read() a=[0]*150 for i in range(0, len(s)-2): if s[i]==s[i+2]: a[ord(s[i+1])] = a[ord(s[i+1])] + 1 ch='' mx=0 for i in range(0, 150): if a[i]>mx: mx=a[i] ch=chr(i) print(ch, mx)
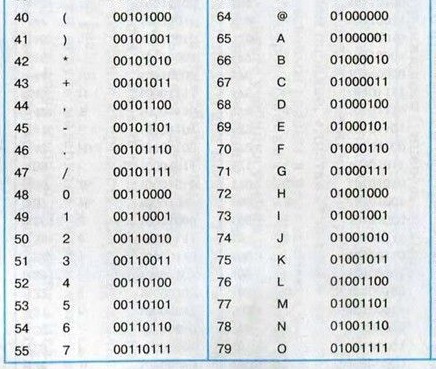
Здесь мы заводим массив a. Индексы этого массива — это коды ANSI всех букв латинского алфавита (ABC…Z). Ведь, как мы знаем, каждая буква кодируется определённым числом (кодом ANSI). Вот часть этой таблицы.
Например, буква A кодируется кодом 65. Коды увеличиваются в алфавитном порядке на 1. Буква Z кодируется числом 90. Таким образом, 150 ячеек точно хватит для нашего алфавита. Здесь берём с запасом, потому что на экзамене можно точно не вспомнить коды, но достаточно запомнить, что 150 ячеек вполне хватит для заглавных и строчных букв латинского алфавита.
Значит, ячейка 65 отвечает за букву A, ячейка 66 отвечает за букву B и т.д. Если мы встретили букву между двумя одинаковыми буквами, то её ячейка увеличивается на 1.
Функция ord() превращает символ в код ANSI.
После того, как мы прошли всю строку и собрали информацию о наших буквах, нужно пройти массив a и найти наибольшее число в нём.
Здесь мы уже не пользуемся функцией max, а используем условие, потому что нужно кроме максимального числа тянуть ещё один параметр — сам код (переменную i). Функция chr() превращает код ANSI обратно в символ.
Ответ: W1608
Задача (Строки различной длины)
Текстовый файл 24-164.txt состоит не более чем из 106 символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Текст разбит на строки различной длины. Необходимо найти строку, содержащую самую длинную цепочку стоящих подряд одинаковых букв. Если таких строк несколько, надо взять ту, которая в файле встретилась раньше. Определите, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая стоит раньше в алфавите. Запишите в ответе эту букву, а затем – сколько раз она встречается во всем файле.
Пример. Исходный файл:
ZZQABA
ZALAAC
QRAQUT
В этом примере в первой и второй строках наибольшая длина цепочек одинаковых буквы равна 2 (ZZ в первой строке, AA во второй), в третьей – 1. Берём первую строку, т.к. она находится в файле раньше. В этой строке чаще других встречаются буквы Z и A (по 2 раза), выбираем букву A, т. к. она стоит раньше в алфавите. В ответе для этого примера надо записать A6, так как во всех строках файла буква A встречается 6 раз.
Решение:
Для считывания построчно файла, будем использовать конструкцию, как в задании 17. В начале найдём строчку, содержащую самую длинную цепочку стоящих подряд одинаковых букв.
f=open('24-164.txt') kmax=0 count=0 n=-1 for s in f.readlines(): count=count+1 k=1 for i in range(0, len(s)-1): if s[i]==s[i+1]: k=k+1 if k>kmax: kmax=k n=count else: k=1 print(n)
Получается строка под номером 162. Переменная count считает строки по порядку. В переменную n сохраняем номер нужной строки. Опять пользуемся условием, а не функцией max, т.к. здесь нужно и обновлять kmax, и сохранять значение n. У нас условие строгое k>kmax, значит, сохранится первая строка с наибольшей искомой цепочкой.
f=open('24-164.txt') count=0 a=[0]*150 for s in f.readlines(): count=count+1 k=1 if count==162: for i in range(0, len(s)): a[ord(s[i])] = a[ord(s[i])] + 1 ch='' mx=0 for i in range(0, 150): if a[i] > mx: mx=a[i] ch=chr(i) print(ch)
Теперь нас интересует только строка под номером 162. Далее используем приём из прошлой задачи. Заводим массив a из 150 ячеек и используем таблицу кодов ANSI. Так определяем какая буква встретилась чаще всего в строке под номером 162. Получается буква K.
f=open('24-164.txt') s=f.read() print(s.count('K'))
Осталось найти количестов букв K во всём файле. Для этого используем функцию .count()
Ответ: K36582
В задаче 15 «Задача (Полезный приём)», созданы переменные k и kmax — напрасно, они не используются.
Убрал, по привычке написал.