Задания
Версия для печати и копирования в MS Word
Тип 10 № 564578
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Спрятать решение
Решение.
По графику
тогда
и
По графику тогда, если
то
— не имеет целочисленных решений,
если то
Значит, и
Найдём наименьший положительный период функции
Наименьший положительный период функции равен
а по графику наименьший положительный период равен 4, тогда
Таким образом, Найдём
Ответ: 1.
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
564578 решу егэ математика профиль
Задание 9 № 564578
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
По графику тогда и
По графику тогда, если то
— не имеет целочисленных решений,
Найдём наименьший положительный период функции
Наименьший положительный период функции равен а по графику наименьший положительный период равен 4, тогда
Задание 9 № 564578
На рисунке изображён график функции вида где числа a, b, c и d целые.
Ege. sdamgia. ru
29.07.2018 19:39:35
2018-07-29 19:39:35
Источники:
Https://ege. sdamgia. ru/problem? id=564578
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 564578 решу егэ математика профиль
564578 решу егэ математика профиль
564578 решу егэ математика профиль
—>
На рисунке изображён график функции. Найдите A.
На рисунке изображён график функции. Найдите B.
На рисунке изображён график функции Найдите A.
На рисунке изображён график функции Найдите B.
На рисунке изображён график функции Найдите A.
На рисунке изображён график функции Найдите B.
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
—>
На рисунке изображён график функции вида где числа a, b, c и d целые.
Ege. sdamgia. ru
05.10.2020 16:08:15
2020-10-05 16:08:15
Источники:
Https://ege. sdamgia. ru/test? theme=191&ttest=true
564578 решу егэ математика профиль — Математика и Английский » /> » /> .keyword { color: red; } 564578 решу егэ математика профиль
564578 решу егэ математика профиль
564578 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509241
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Заметим, что уравнение прямой имеет вид Y = Kx + B.
Найдём уравнение функции, отмеченной на рисунке оранжевым цветом. Заметим, что K — тангенс угла наклона прямой, По графику, F(−1) = −1, отсюда Следовательно, уравнение прямой имеет
Найдём уравнение функции, отмеченной на рисунке синим цветом. Заметим, что K — тангенс угла наклона прямой, По графику, F(2) = −1, отсюда Следовательно, уравнение прямой имеет вид
Задание 9 № 509241
Заметим, что уравнение прямой имеет вид y kx b.
Источники:
564578 решу егэ математика профиль
564578 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 564578
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
По графику тогда и
По графику тогда, если то
— не имеет целочисленных решений,
Найдём наименьший положительный период функции
Наименьший положительный период функции равен а по графику наименьший положительный период равен 4, тогда
Источники:
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 564578
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
По графику тогда и
По графику тогда, если то
— не имеет целочисленных решений,
Найдём наименьший положительный период функции
Наименьший положительный период функции равен а по графику наименьший положительный период равен 4, тогда
Задание 9 509241.
Dankonoy. com
01.01.2019 12:36:56
2019-01-01 12:36:56
Источники:
Https://dankonoy. com/ege/ege12/archives/473
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Положительное действительное
число 564578
– составное число.
Произведение всех цифр числа: 33600.
У числа 564578 16 делителей.
988800 — сумма делителей.
Обратное число к 564578 – это 0.0000017712344441334944.
Это число представляется произведением: 2 * 7 * 7 * 7 * 823.
Другие представления числа 564578:
двоичная система счисления: 10001001110101100010, троичная система счисления: 1001200110022, восьмеричная система счисления: 2116542, шестнадцатеричная система счисления: 89D62.
В числе байт 564578 содержится 551 килобайт 354 байта информации.
В виде кода азбуки Морзе: ….. -…. ….- ….. —… —..
Число 564578 не является числом Фибоначчи.
Косинус 564578: -0.7266, тангенс 564578: -0.9455, синус 564578: 0.6870.
Натуральный логарифм числа равен 13.2438.
Десятичный логарифм числа равен 5.7517.
751.3841 — квадратный корень, 82.6497 — кубический корень.
Число в квадрате это 3.1875e+11.
6 дней 12 часов 49 минут 38 секунд представляет из себя число секунд 564578.
Нумерологическое значение числа 564578 – цифра 8.
В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.
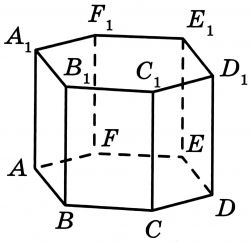
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac19right)^{x+4}=729)
Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)
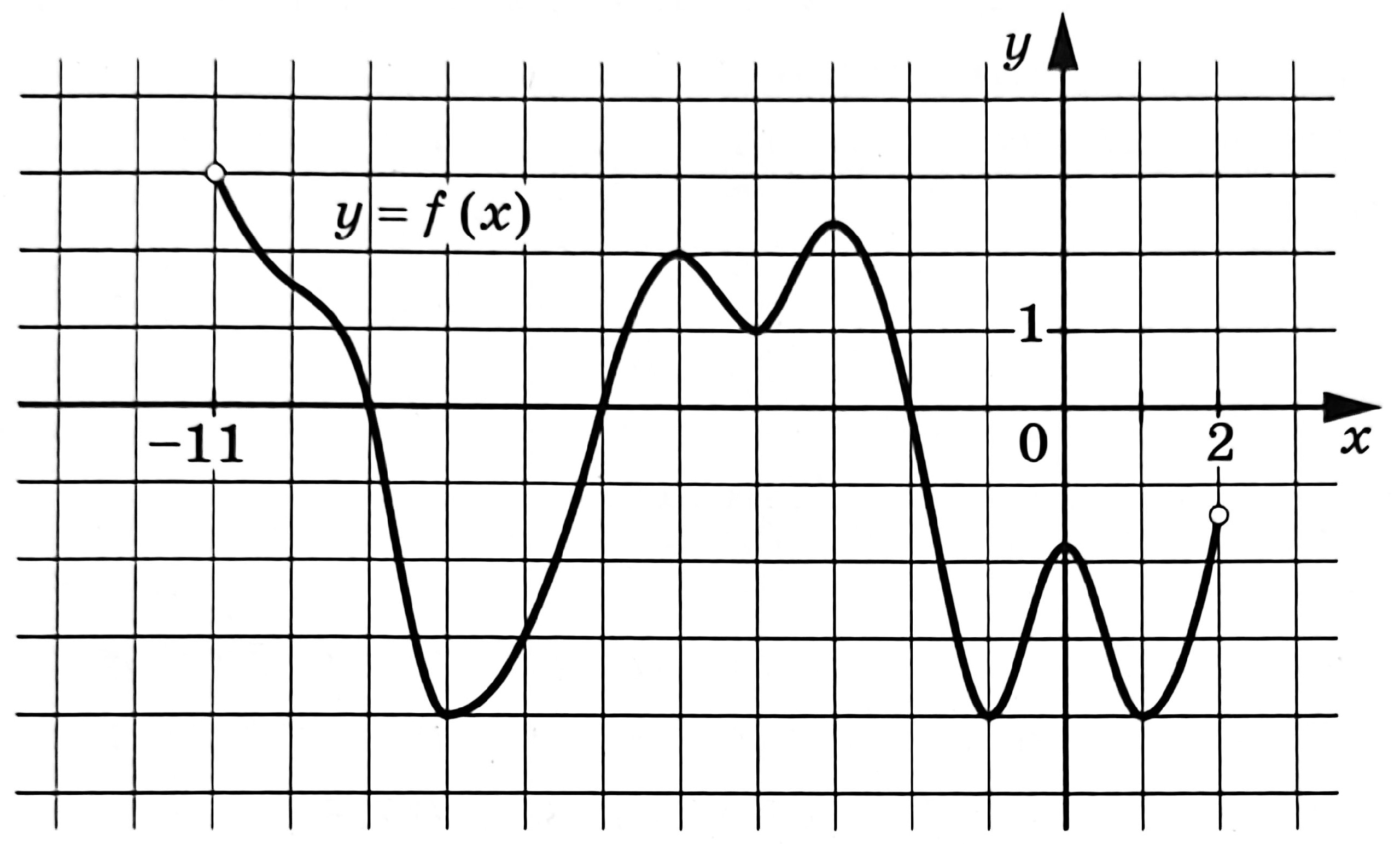
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
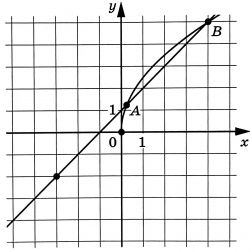
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.
Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])
а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решение и ответы заданий Варианта №3 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.

Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
Площадь ромба равна 10. Одна из его диагоналей равна 8. Найдите другую диагональ.
Задание 2.
Длина окружности основания цилиндра равна 5, высота равна 6. Найдите площадь боковой поверхности цилиндра.
Задание 3.
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,83. Вероятность того, что окажется меньше 10 пассажиров, равна 0,46. Найдите вероятность того, что число пассажиров будет от 10 до 20.
Задание 4.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Биолог» выиграет жребий ровно два раза.
Задание 5.
Найдите корень уравнения cosfrac{pi(2x–6)}{6}=frac{sqrt{3}}{2}. В ответе запишите наибольший отрицательный корень.
Задание 6.
Найдите значение выражения frac{4^{4,75}}{8^{2,5}}.
Задание 7.
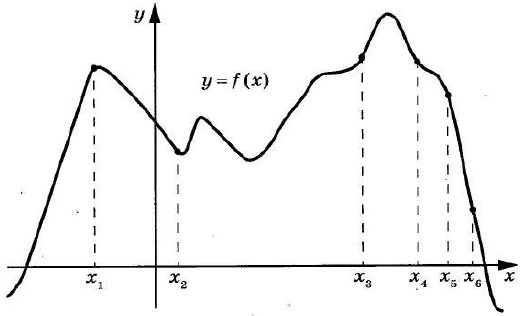
На рисунке изображён график функции y = f(x). На оси абсцисс отмечено шесть точек: x1, x2, x3, x4, x5, x6. В ответе укажите количество точек (из отмеченных) в которых производная функции f(x) положительна?
Задание 8.
Наблюдатель находится на высоте h, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле l=sqrt{frac{Rh}{500}}, где R = 6400 км – радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 25,6 километра? Ответ дайте в метрах.
Задание 9.
Заказ на изготовление 238 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 3 детали больше?
Задание 10.
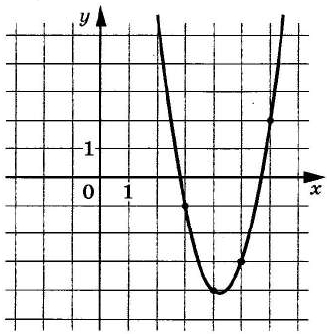
На рисунке изображён график функции f(x) = ax2 + bc + c. Найдите с.
Задание 11.
Найдите наибольшее значение функции y = ln(x + 18)12 − 12x на отрезке [−17,5;0].
Задание 12.
а) Решите уравнение 4^{x+sqrt{x}–1,5}+3cdot 4^{x–sqrt{x}+1,5}-4^{x+1}=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [2; 6].
Задание 13.
В прямой пятиугольной призме ABCDEA1B1C1D1E1, высота АА1, равна 3√5, BC = CD = 6, а четырехугольник ABDE прямоугольник со сторонами АВ = 5 и AE = 4√5.
а) Докажите, что плоскости СA1E1 и AED1 перпендикулярны.
б) Найдите объём многогранника CAED1B1.
Задание 14.
Решите неравенство logtg3,2 (log3 (9 – x2)) ≥ 0.
Задание 15.
В июле Максим планирует взять кредит в банке на некоторую сумму. Банк предложил Максиму два варианта кредитования.
1-й вариант:
– кредит предоставляется на 3 года;
– в январе каждого года действия кредита долг увеличивается на 20% от суммы долга на конец предыдущего года;
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платеж должен погасить долг по кредиту полностью,
2-й вариант:
– кредит предоставляется на 2 года:
– в январе каждого года действия кредита долг увеличивается на 24 %;
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Когда Максим подсчитал, то выяснил, что по 1-му варианту кредитования ему придется выплачивать на 373 600 рублей больше, чем по 2-му варианту. Какую сумму Максим планирует взять в кредит?
Задание 16.
Четырёхугольник ABCD со сторонами ВС = 7 и AB = CD = 20 вписан в окружность радиусом R = 16.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
frac{log_{0,4}(6x^{2}–13x+5ax–6a^{2}–13a+6)}{sqrt{2x–3a+4}}=0
имеет единственный корень.
Задание 18.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 9177.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из пяти членов?
в) Какое наибольшее количество членов может быть в последовательности?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.