Задание 12 егэ математика профиль степенные функции
Задание 11 № 77460
Найдите наименьшее значение функции на отрезке
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
Если подставить в функцию значение х=1 то будет ответ y=-1, почему мы его не учитываем? ведь в этой точке тоже существует функция
По рисунку видно (по стрелочкам), что функция принимает своё наименьшее (самое низкое) значение при x=4, поэтому рассматривать значение при х=1 не имеет смысла.
Задание 11 № 77460
Найдем нули производной.
Math-ege. sdamgia. ru
07.11.2018 7:06:13
2018-11-07 07:06:13
Источники:
Https://math-ege. sdamgia. ru/problem? id=77460
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 12 егэ математика профиль степенные функции
Задание 12 егэ математика профиль степенные функции
Задание 12 егэ математика профиль степенные функции
Задание 11 № 77419
Найдите точку максимума функции
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума
Скажите, пожалуйста, чтобы определить знак интервала, мы должны числа подставлять в уравнение производной или в данное уравнение? Спасибо за ответ.
Добрый день! В уравнение производной, её знак мы и определяем.
Задание 11 № 77421
Найдите наименьшее значение функции на отрезке
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
А почему получаем -54?
Ведь 3 подставляем в уравнение y’=3x^-27
Значит будет y=27-27=0
Подставлять нужно в изначальную функцию, а не в ее производную.
Задание 11 № 77422
Найдите наибольшее значение функции на отрезке
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
Задание 11 № 77421
Задание 11 № 77419
В уравнение производной, её знак мы и определяем.
Ege. sdamgia. ru
04.07.2018 13:06:21
2018-07-04 13:06:21
Источники:
Https://ege. sdamgia. ru/test? theme=81
Задание 12 ЕГЭ по математике профильного уровня 2022: теория и практика » /> » /> .keyword { color: red; } Задание 12 егэ математика профиль степенные функции
Задание 12. Уравнения. ЕГЭ 2022 по математике профильного уровня
Задание 12. Уравнения. ЕГЭ 2022 по математике профильного уровня
За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: Повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть Развернутый ответ (полная запись решения с обоснованием выполненных действий).
Задачи для практики
Задача 1
А) Решите уравнение $11cos 2x=7sin (x — / )-9$.
Б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
Б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
Задача 2
А) Решите уравнение $2 sin^2 x — 7 cos(x + /)- 4 = 0$.
Б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-/]$.
Решение
А) Преобразуем уравнение, согласно формуле приведения:
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$t_1 = / = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
Вернёмся к исходной переменной:
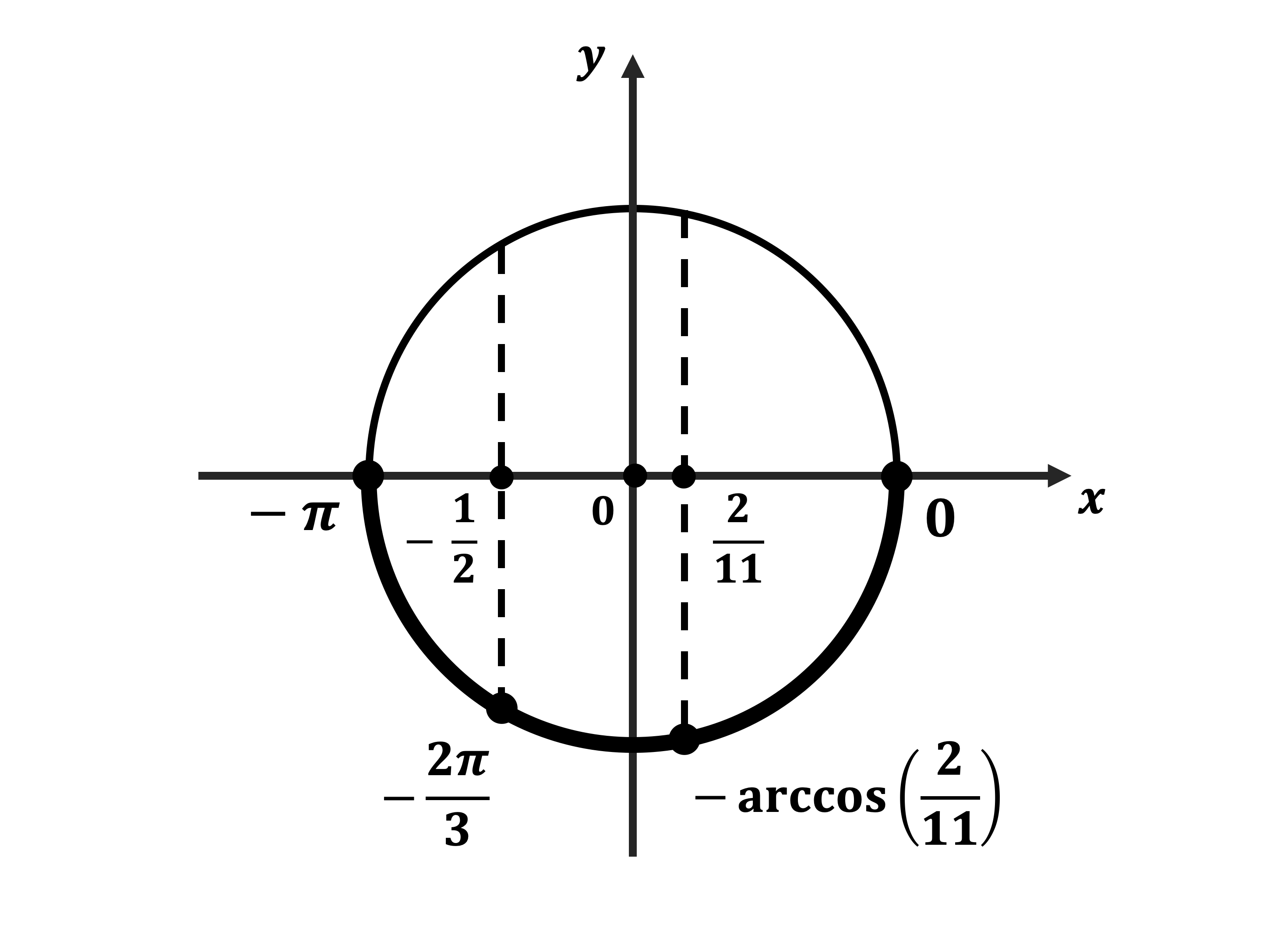
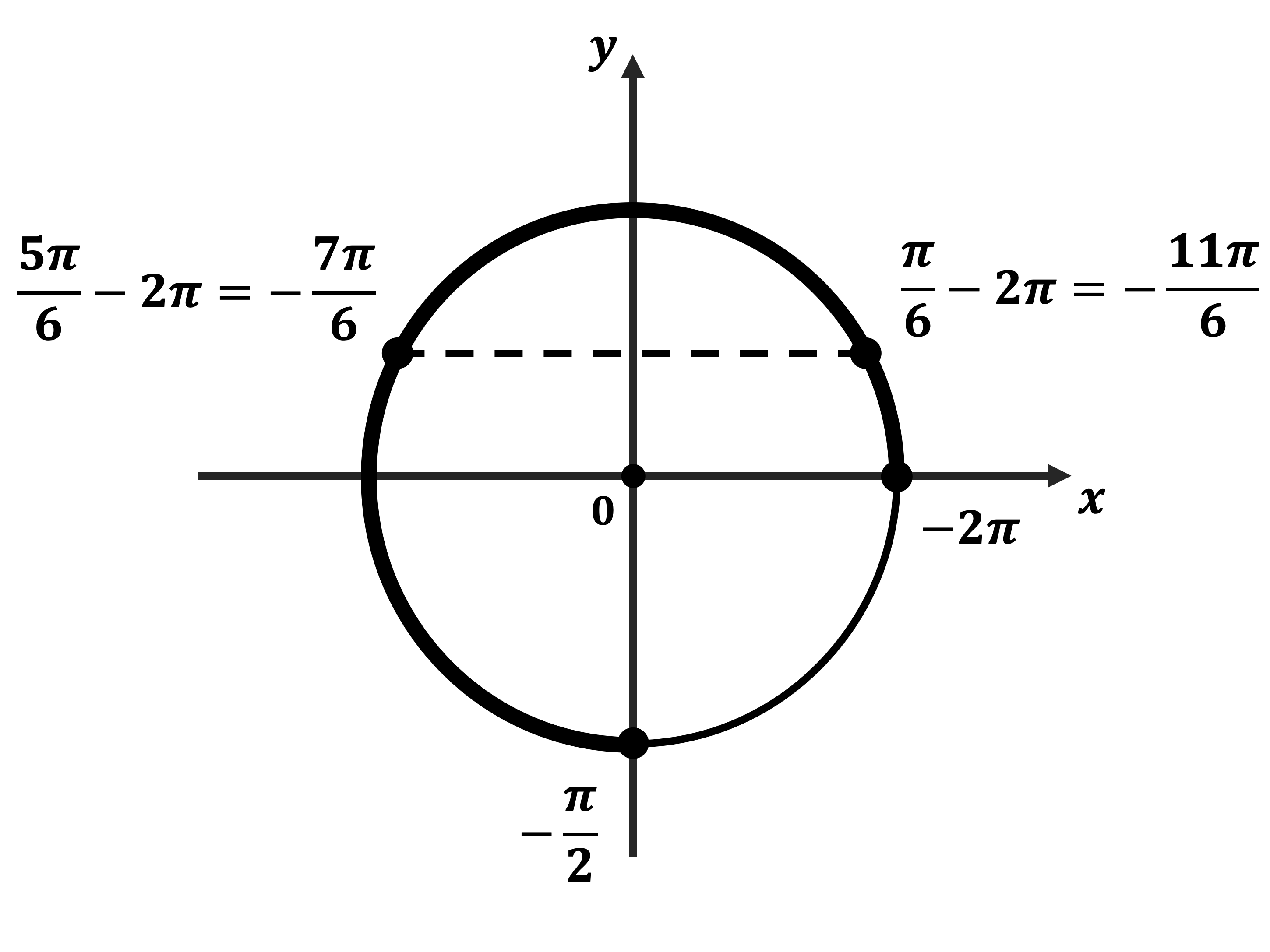
Б) Корни, принадлежащие отрезку $[-2π; -/]$, найдём с помощью единичной окружности. Получим: $/-2π=-/; /-2π=-/$.
Задача 3
А) Решите уравнение $2 cos^2 x — 5 sin(x + /)+ 2 = 0$.
Б) Найдите все корни этого уравнения, принадлежащие промежутку $[/;/]$.
Решение
А) Преобразуем уравнение, согласно формуле приведения:
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = / = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = / = −/$.
Вернёмся к исходной переменной: $cos x = − /$,
$x = ±(π − /) + 2πn, n ∈ Z, x = ±/ + 2πn, n ∈ Z.$
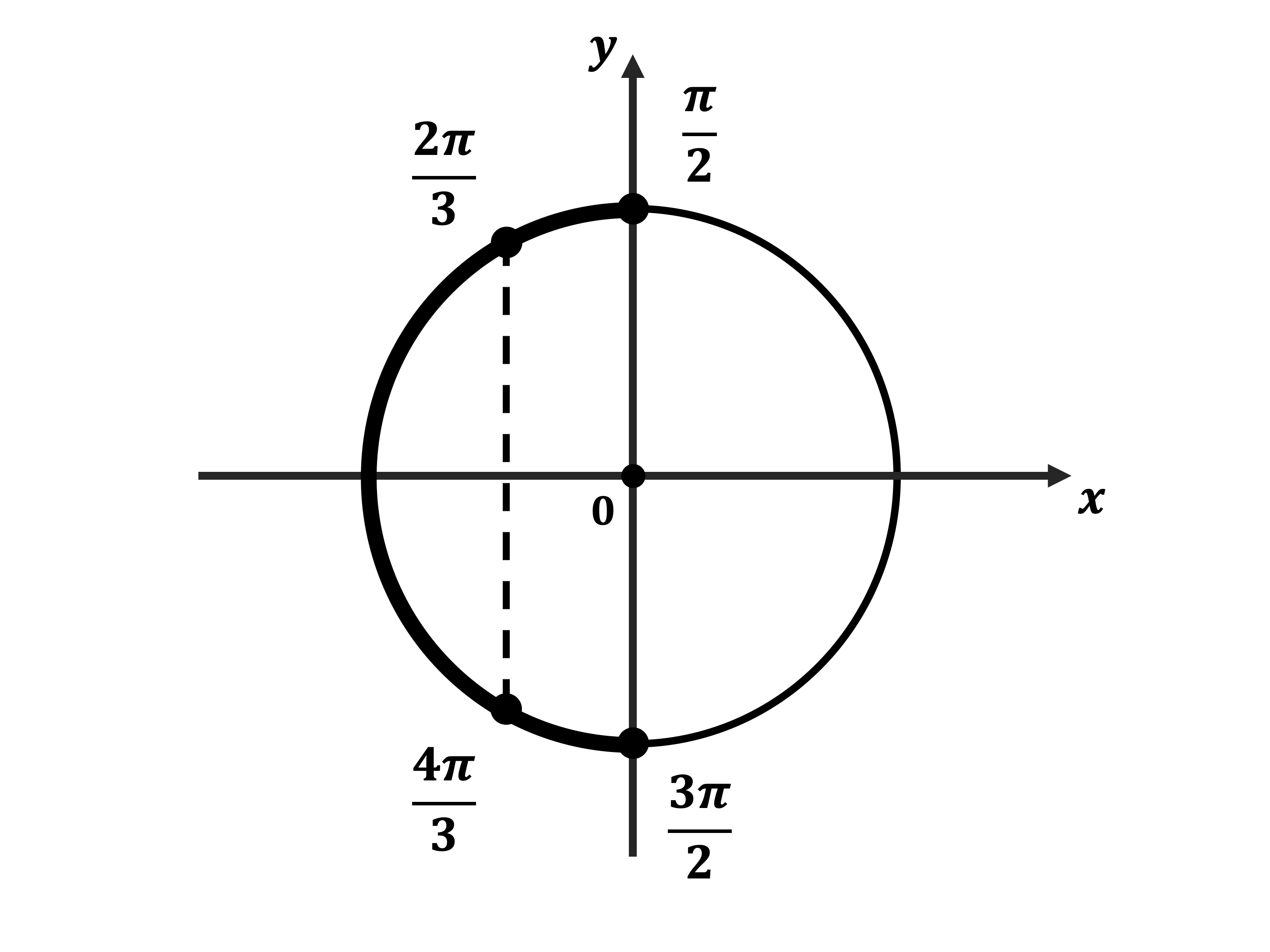
Б) Корни, принадлежащие отрезку $[/; /]$, найдём с помощью единичной окружности. Получим числа $/; /$.
Задача 4
А) Решите уравнение $cos(x — /)= sin 2x$.
Б) Найдите все корни этого уравнения, принадлежащие промежутку $[-/;0]$.
Решение
А) Преобразуем уравнение:
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
$sin x = 0;x = πn, n ∈ Z,$
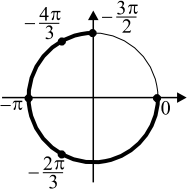
Б) Корни, принадлежащие отрезку $[-/;0]$, найдём с помощью единичной окружности. Получим числа $−/; −π; −/; 0$.
Задача 5
А) Решите уравнение $sin(/+ x)= sin (-2x)$.
Б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
А) Преобразуем уравнение:
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
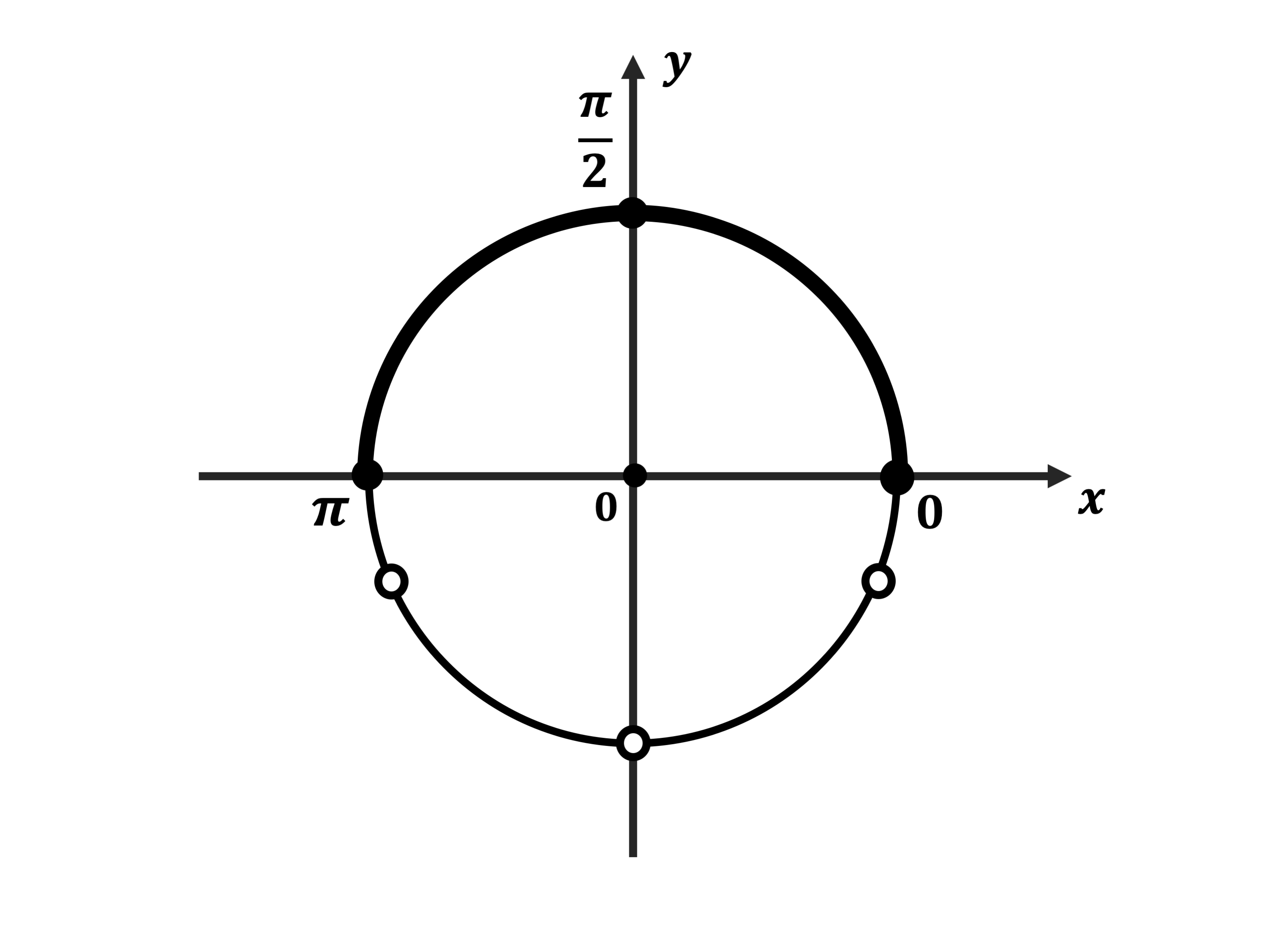
Б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число $/$.
Задача 6
А) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin /= 0$.
Б) Найдите все корни этого уравнения, принадлежащие промежутку $[-/;π]$.
Решение
А) Решим уравнение $sinx(2sinx-1) +√3sinx + sin/ = 0$.
Так как $sin/ = sin(π +/) = − sin/ = −/$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-/ = 0$. Отсюда $2 sin x(sin x-/)+ √3(sin x-/) = 0; (2sinx+√3)(sin x-/) = 0$.
Тогда $sin x = /; x = (−1)^n/ + πn$ или $sin x = −/; x = (−1)^/ + πn$, где $n ∈ Z.$
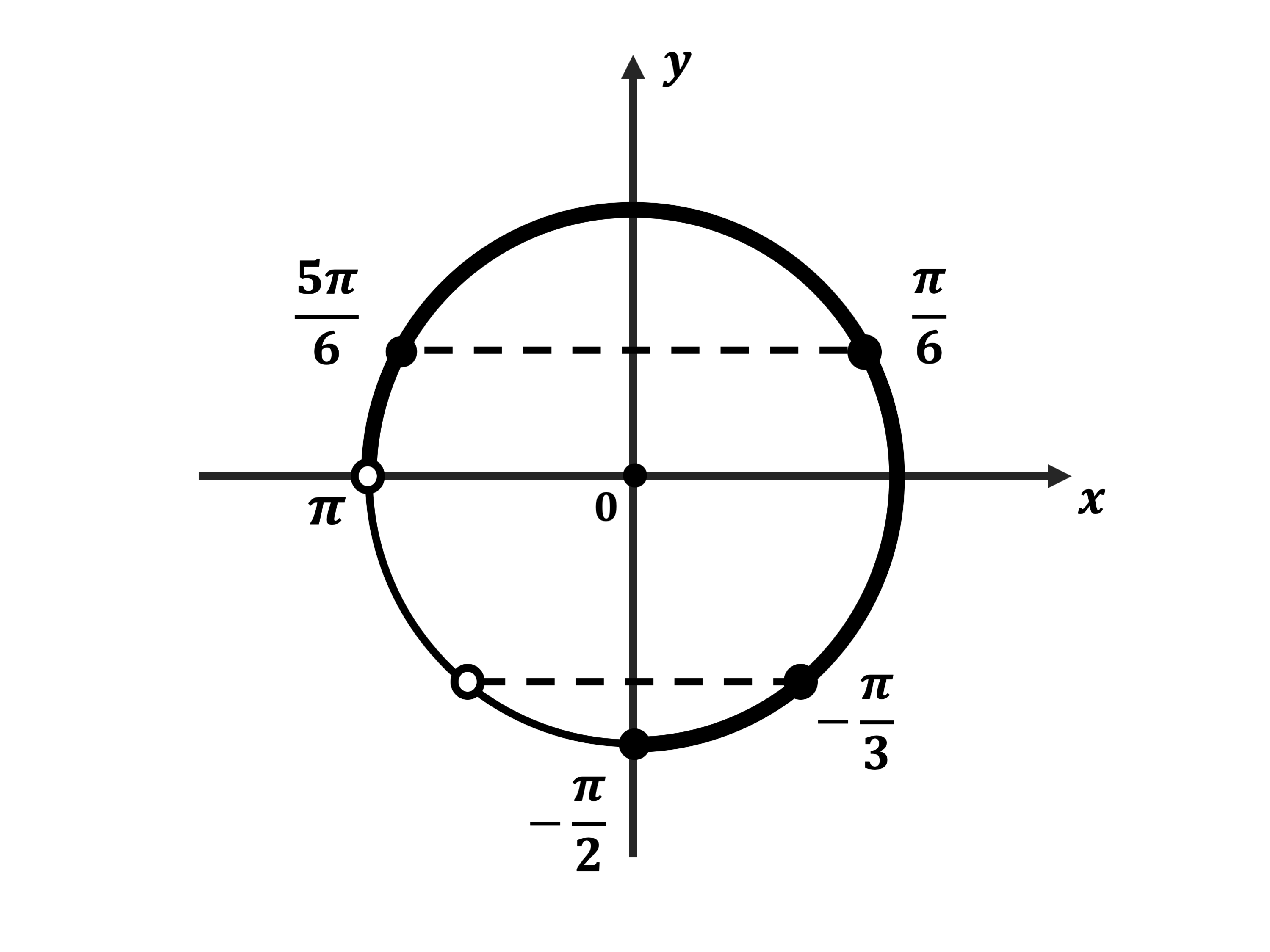
Б) Корни, принадлежащие промежутку $[−/; π]$, найдём с помощью числовой окружности: $−/; /; /$.
Задача 7
А) Решите уравнение $4cos^x = 3cos2x + 1$.
Б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-/)$.
Решение
A) $4cos^x = 3cos2x+1$,
$cos^x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
Б) Корни, принадлежащие промежутку $[-4π;-/)$, найдем из неравенства $-4π ≤ πk ×
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Задание 12. Уравнения. ЕГЭ 2022 по математике профильного уровня
За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: Повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть Развернутый ответ (полная запись решения с обоснованием выполненных действий).
А) Решите уравнение $11cos 2x=7sin (x — / )-9$.
Б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
Б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
T_1 4 не удовлетворяет условию 1 t 1.
Egeturbo. ru
15.04.2018 7:29:26
2018-04-15 07:29:26
Источники:
Https://egeturbo. ru/ege/math/tasks/12
Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
▶Скачать вариант с ответами
▶Решение заданий с 1 по 18
▶Распечатай и реши вариант
вариант_26_егэ2023_профиль_математика
Ответы и решения
решение_варианта_26_профиль
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, sin 𝐴 = 0,8. Найдите sin 𝐵.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
7. На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3; 8). Найдите точку из отрезка [−2; 5], в которой производная функции 𝑓(𝑥) равна 0.
8. Два тела, массой 𝑚 = 2 кг каждое, движутся с одинаковой скоростью 𝑣 = 8 м/с под углом 2𝛼 друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле 𝑄 = 𝑚𝑣 2 sin2𝛼, где 𝑚 − масса (в кг), 𝑣 − скорость (в м/с). Найдите, под каким углом 2𝛼 должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
9. Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Найдите значение 𝑓(−2).
11. Найдите точку максимума функции 𝑦 = ln(𝑥 + 9) − 10𝑥 + 7.
12. а) Решите уравнение 3 ∙ 9 𝑥+1 − 5 ∙ 6 𝑥+1 + 8 ∙ 2 2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13. В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 все рёбра равны 2. Точка 𝑀 − середина ребра 𝐴𝐴1. а) Докажите, что прямые 𝑀𝐵 и 𝐵1𝐶 перпендикулярны. б) Найдите расстояние между прямыми 𝑀𝐵 и 𝐵1𝐶.
15. В июле 2016 года планируется взять кредит в банке на три года в размере 𝑆 млн рублей, где 𝑆 − целое число. Условия его возврата таковы: – каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение 𝑆, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
16. В трапеции 𝐴𝐵𝐶𝐷 боковая сторона 𝐴𝐵 перпендикулярна основаниям. Из точки 𝐴 на сторону 𝐶𝐷 опустили перпендикуляр 𝐴𝐻. На стороне 𝐴𝐵 отмечена точка 𝐸 так, что прямые 𝐶𝐷 и 𝐶𝐸 перпендикулярны. а) Докажите, что прямые 𝐵𝐻 и 𝐸𝐷 параллельны. б) Найдите отношение 𝐵𝐻 к 𝐸𝐷, если ∠𝐵𝐶𝐷 = 135°.
18. В течение 𝑛 дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли 𝑛 быть больше 5? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 3, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 6. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2013-01-19

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |