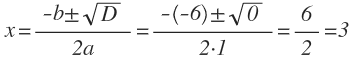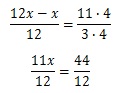Решу егэ 9 задание дискриминант - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Линейные, квадратные, кубические уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 5 № 26662

Найдите корень уравнения:

Аналоги к заданию № 26662: 10149 9653 9659 9667 9669 9673 9677 9679 9691 9693 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 26663

Найдите корень уравнения:

Аналоги к заданию № 26663: 9655 10135 9657 9661 9663 9665 9671 9675 9681 9683 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77368

Решите уравнение

Аналоги к заданию № 77368: 100259 100757 509597 509988 510118 513336 513357 100261 100263 100265 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77369

Решите уравнение

Аналоги к заданию № 77369: 100759 100787 100761 100763 100765 100767 100769 100771 100773 100775 … Все

Решение

Курс Д. Д. Гущина

2 комментария · Сообщить об ошибке · Помощь

Тип 5 № 77371

Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Аналоги к заданию № 77371: 100881 101379 524042 624069 624103 100883 100885 100887 100889 100891 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

3 комментария · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 193 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

а)  Существуют ли натуральные числа m и n, такие, что дискриминант квадратного трехчлена равен 33?

б)  Существуют ли натуральные числа m и n, такие, что дискриминант квадратного трехчлена равен 26?

в)  Какое наименьшее значение принимает дискриминант D квадратного трехчлена если известно, что числа m, n и D  — натуральные?

Источник: Задания 18 ЕГЭ–2020, Задания 19 ЕГЭ–2020

а)  Существуют ли натуральные числа m и n, такие, что дискриминант квадратного трехчлена равен 17?

б)  Существуют ли натуральные числа m и n, такие, что дискриминант квадратного трехчлена равен 54?

Источник: ЕГЭ по математике 25.07.2020. Резервная волна. Вариант 3

Найдите все значения а, при каждом из которых уравнение имеет ровно три различных корня.

Источник: А. Ларин: Тренировочный вариант № 90.

Найдите все значения параметра а, при каждом из которых система

имеет ровно одно решение.

Источник: А. Ларин: Тренировочный вариант № 92.

Найдите все значения параметра a, при каждом из которых система уравнений

имеет ровно четыре различных решения.

Источник: Избранные задания по математике из последних сборников ФИПИ

Найдите все значения параметра a, при котором система уравнений

имеет ровно четыре различных решения.

Источник: Избранные задания по математике из последних сборников ФИПИ

Найдите все значения a, при которых уравнение на промежутке имеет ровно два корня.

Найдите все значения а, при каждом из которых уравнение

имеет ровно один корень.

Источник: А. Ларин: Тренировочный вариант № 121.

Найдите все значения параметра а, при которых система неравенств

имеет ровно одно решение.

Источник: А. Ларин. Тренировочный вариант № 339.

Прямая является касательной к графику функции Найдите b, учитывая, что абсцисса точки касания больше 0.

При каких значениях параметра a для любых значений параметра b хотя бы при одном значении параметра с система уравнений

имеет решения?

Всего: 193 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

$a$ — старший коэффициент;
$b$ — средний коэффициент;
$c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0 х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение полного квадратного уравнения

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $3³

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

найти общий знаменатель дробей, входящих в уравнение;
умножить обе части уравнения на общий знаменатель;
решить получившееся целое уравнение;
исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

${3х-5}/{-2}={1}/{х}$

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х (3х — 5) = -2$

Раскроем скобки и соберем все слагаемые в левой части уравнения

$3х^2- 5х + 2 = 0$

Решим данное квадратное уравнение первым устным способом, т.к.

$a + b + c = 0$

$x_1 = 1, x_2 = {2}/{3}$

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1 = 1, x_2 = {2}/{3}$

Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.

Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.

Например,

${2}/{x}+5x=7$ – рациональное уравнение

$3x+√x=7$ — иррациональное уравнение (содержит корень)

Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
Найти общий знаменатель дробей, входящих в уравнение;
Умножить обе части уравнения на общий знаменатель;
Решить получившееся целое уравнение;
Исключить из его корней те, которые обращают в ноль общий знаменатель.

Решить уравнение: $4x+1-{3}/{x}=0$

Решение:

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x ≠ 0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x+1-{3}/{x}=0|·x$

$4x·x+1·x-{3·x}/{x}=0$

3. решаем полученное уравнение

$4x^2+x-3=0$

Решим вторым устным способом, т.к. $а+с=b$

Тогда, $x_1=-1, x_2=-{3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю

Ответ: $x_1=-1, x_2=-{3}/{4}$

При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$

Решить уравнение ${3x-5}/{-2}={1}/{x}$

Решение:

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х(3х-5)=-2$

Раскроем скобки и соберем все слагаемые в левой стороне

$3х^2-5х+2=0$

Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$

$x_1=1, x_2={2}/{3}$

В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=1, x_2={2}/{3}$

Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.

Чтобы решить иррациональное уравнение, необходимо:

Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
Решить полученное рациональное уравнение.
Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.

Решение:

Обе части уравнение возведем в квадрат:

$√{4х-3}^2=х^2$

Получаем квадратное уравнение:

$4х-3=х^2$

Перенесем все слагаемые в левую часть уравнения:

${-х}^2+4х-3=0$

Решим данное квадратное уравнение устным способом, так как

$a+b+c=0$

$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$√{4·1-3}=1$

$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.

$√{4·(3)-3}=3$

$√9=3$

$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит

$х_1=1$ наименьший корень.

Ответ: $1$

Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$

Решить уравнение: $х-6=√{8-х}$

Возведем обе части уравнения в квадрат

$(х-6)^2=8-х$

В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение

$х^2-2·6·х+6^2=8-х$

$х^2-12х+36=8-х$

Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.

$х^2-12х+36-8+х=0$

Приводим подобные слагаемые:

$х^2-11х+28=0$

Найдем корни уравнения через дискриминант:

$D=b^2-4ac=121-4·28=121-112=9=3^2$

$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$

$x_1=7; x_2=4$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$x_1=7$

$7-6=√{8-7}$

$1=1$, получили верное равенство, следовательно, корень нам подходит.

$x_2=4$

$4-6=√{8-4}$

$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.

Ответ: $7$

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n⋅a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.

Решить уравнение $25·5^х=1$

Решение:

В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$

$5^2·5^х=5^0$

При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются

$5^{2+х}=5^0$

Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели

$2+х=0$

$х=-2$

Ответ: $-2$

Решить уравнение $2^{3х+2}-2^{3х-2}=30$

Решение:

Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель

$2^{3x+2}-2^{3x-2}=30$

$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$

$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$

$2^{3x-2}(2^4-1)=30$

$2^{3x-2}·15=30$

Разделим обе части уравнения на $15$

$2^{3х-2}=2$

$2^{3х-2}=2^1$

$3х-2=1$

$3х=3$

$х=1$

Ответ: $1$

Источник

Подготовка к ОГЭ. Решение квадратных уравнений

Алгоритм решения квадратного уравнения, образец для решения и задания для самостоятельной подготовки.

Бланки ЕГЭ 2022

Полный комплект бланков ЕГЭ 2022.

Задачи на объём

Метод объёмов. Важная формула. Стереометрия с нуля.

Подросткам с 14 лет разрешили регистрироваться на госуслугах

Несовершеннолетние граждане смогут стать пользователями единого портала госуслуг. Постановление об этом подписал Председатель Правительства Михаил Мишустин.

Уравнение из огэ 9 класс дискриминант

Найдите корни уравнения .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.

Тем самым, это числа −2 и 3.

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Запишем уравнение в виде По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.

Как найти дискриминант квадратного уравнения

О чем эта статья:

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

Определим коэффициенты: a = 3, b = -4, c = 2.
Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

Определим коэффициенты: a = 1, b = -6, c = 9.
Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

Определим коэффициенты: a = 1, b = -4, c = -5.
Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

источники:

http://oge.sdamgia.ru/test?theme=43

http://skysmart.ru/articles/mathematic/kak-najti-diskriminant-kvadratnogo-uravneniya

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Квадратные и линейные уравнения

Линейное уравнение – уравнение, сводящееся к виду (large{ax+b=0}), где (ane
0, b) – числа.
Линейное уравнение всегда имеет единственное решение (x=-dfrac ba).

Квадратное уравнение – уравнение, сводящееся к виду (large{ax^2+bx+c=0}), где (ane
0,b,c) – числа.
Выражение (D=b^2-4ac) называется дискриминантом квадратного уравнения.
Квадратное уравнение может иметь не более двух корней:

(bullet) если (D>0), то оно имеет два различных корня

[x_1=dfrac{-b+sqrt{D}}{2a} quad text{и} quad x_2=dfrac{-b-sqrt{D}}{2a}]

(bullet) если (D=0), то оно имеет один корень (иногда говорят, что два совпадающих)

[x_1=x_2=-dfrac{b}{2a}]

(bullet) если (D<0), то оно не имеет корней.

(blacktriangleright) Теорема Виета для квадратного уравнения:

Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения

[{large{x_1+x_2=-dfrac{b}{a}}}]

а произведение

[{large{x_1cdot x_2=dfrac{c}{a}}}]

(blacktriangleright) Если квадратное уравнение:

(sim) имеет два корня (x_1) и (x_2), то (ax^2+bx+c=a(x-x_1)(x-x_2)).

(sim) имеет один корень (x_1) (иногда говорят, что два совпадающих), то (ax^2+bx+c=a(x-x_1)^2).

(sim) не имеет корней, то квадратный трехчлен (ax^2+bc+c) никогда не может быть равен нулю. Более того, он при всех (x) строго одного знака: либо положителен, либо отрицателен.

(blacktriangleright) Полезные формулы сокращенного умножения:

[begin{aligned}
&x^2-y^2=(x-y)(x+y)\
&(x+y)^2=x^2+2xy+y^2\
&(x-y)^2=x^2-2xy+y^2
end{aligned}]

Задание
1

#305

Уровень задания: Равен ЕГЭ

Найдите корень уравнения (dfrac{2}{9}x = 4dfrac{1}{9}).

ОДЗ: (x) – произвольное. Решим на ОДЗ:

Умножим левую и правую часть уравнения на 9. После умножения: (2x = 37), что равносильно (x = 18,5) – подходит по ОДЗ.

Ответ: 18,5

Задание
2

#306

Уровень задания: Равен ЕГЭ

Найдите корень уравнения (-dfrac{4}{3}x = 5dfrac{2}{3}).

ОДЗ: (x) – произвольное. Решим на ОДЗ:

Умножим левую и правую часть уравнения на (-3). После умножения: (4x = -17), что равносильно (x = -4,25) – подходит по ОДЗ.

Ответ: -4,25

Задание
3

#310

Уровень задания: Равен ЕГЭ

Найдите корень уравнения (x^2 — 11x + 28 = 0). Если уравнение имеет более одного корня, в ответе укажите больший из них.

ОДЗ: (x) – произвольное. Решим на ОДЗ:

Дискриминант данного уравнения (D = 121 — 28 cdot 4 = 121 — 112 = 9 = 3^2). Корни [x_1 = dfrac{11 + 3}{2} = 7, x_2 = dfrac{11 — 3}{2} = 4] – подходят по ОДЗ. Ответ: (x = 7) – больший корень уравнения.

Ответ: 7

Задание
4

#311

Уровень задания: Равен ЕГЭ

Найдите корень уравнения (2x^2 — 7x + 3 = 0). Если уравнение имеет более одного корня, в ответе укажите меньший из них.

ОДЗ: (x) – произвольное. Решим на ОДЗ:

Дискриминант данного уравнения (D = 49 — 24 = 25 = 5^2). Корни (x_1 = dfrac{7 + 5}{4} = 3, x_2 = dfrac{7 — 5}{4} = 0,5) – подходят по ОДЗ. Ответ: (x = 0,5) – меньший корень уравнения.

Ответ: 0,5

Задание
5

#312

Уровень задания: Равен ЕГЭ

Найдите корень уравнения ((4x + 5)^2 = (4x + 4)^2).

ОДЗ: (x) – произвольное. Решим на ОДЗ:

После упрощения имеем (16x^2 + 40x + 25 = 16x^2 + 32x + 16), что равносильно (8x = -9), откуда (x = -1,125) – подходит по ОДЗ.

Ответ: -1,125

Задание
6

#314

Уровень задания: Равен ЕГЭ

Найдите корень уравнения ((5x + 8)^2 = 160x).

ОДЗ: (x) – произвольное. Решим на ОДЗ:

После упрощения имеем (25x^2 + 80x + 64 = 160x), что равносильно (25x^2 — 80x + 64 = 0), что равносильно ((5x — 8)^2 = 0), что равносильно ((5x — 8)(5x — = 0).

Произведение двух выражений равно нулю в том и только том случае, когда хотя бы одно из них равно 0 и оба выражения не теряют смысл. Отсюда заключаем, что [x = dfrac{8}{5} = 1,6] – единственный корень – подходит по ОДЗ.

Ответ: 1,6

Задание
7

#315

Уровень задания: Равен ЕГЭ

Найдите корень уравнения ((2x + 11)^2 = 88x).

ОДЗ: (x) – произвольное. Решим на ОДЗ:

После упрощения имеем (4x^2 + 44x + 121 = 88x), что равносильно (4x^2 — 44x + 121 = 0), что равносильно ((2x — 11)^2 = 0), что равносильно ((2x — 11)(2x — 11) = 0).

Произведение двух выражений равно нулю в том и только том случае, когда хотя бы одно из них равно 0 и оба выражения не теряют смысл. Отсюда заключаем, что [x = dfrac{11}{2} = 5,5] – единственный корень – подходит по ОДЗ.

Ответ: 5,5

Знакомство школьника с квадратными уравнениями вида (ax²+bx+c=0), где (ane 0), (b), (c) — заданные числа, происходит еще задолго до сдачи ЕГЭ по математике в Москве или любом другом городе РФ, а именно в 8 классе. Несмотря на то, что на изучение материала по данной теме, как правило, отводится немало времени, далеко не все школьники с легкостью решают подобные задачи. Поэтому, готовясь к сдаче выпускного экзамена, школьникам как в Москве, так и в других населенных пунктах РФ необходимо повторить такой раздел алгебры, как квадратные уравнения: в ЕГЭ по математике они обязательно встретятся.

Для того чтобы освежить в памяти основные способы решения подобного задания и способы решения иррациональных уравнений, воспользуйтесь образовательным проектом «Школково». Наши специалисты подготовили для вас в максимально понятной и доступной форме теоретический материал по теме «Квадратные уравнения», подобрали интересные примеры, которые встречаются в ЕГЭ, а также их подробные решения.

Необходимо запомнить

Для решения квадратных уравнений в ЕГЭ по математике следует выучить формулу, по которой вычисляется дискриминант. Она довольная простая: (D=b2−4ac).

Квадратное уравнение, которое вам предстоит решить в ЕГЭ, может иметь не более двух корней. Если вычисленный дискриминант больше 0, то следует использовать следующие формулы:

(x_1=dfrac{-b+sqrt{D}}{2a})

(x_2=dfrac{-b-sqrt{D}}{2a})

Если D = 0, то уравнение имеет один корень (иногда говорят, что 2 равных):

(x_1=x2=dfrac{-b}{2a})

Если дискриминант меньше 0, то уравнение не имеет корней.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задание 1

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

Решение(по дискриминанту).

D=(-1)²

₁₌₂₌

Ответ: −23.

1. Задание 1

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

2. Задание 1

Решите уравнение 8x² −
12x + 4 = 0.

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

3. Задание 1

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

4. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

5. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите больший из корней.

6. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

7. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите больший из корней.

8. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

9. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

10. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

11. Задание 1

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 2

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

Решение.

Запишем уравнение в виде

Далее решаем по дискриминанту.

1. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

2. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

3. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

4. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

5. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

6. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

7. Задание 2

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

8. Задание 2

Решите уравнение

Если уравнение имеет более одного корня, в
ответ запишите больший из корней.

9. Задание 2

Решите уравнение .

10. Задание 2

Решите уравнение .

Задание 3

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

Решение.

Запишем уравнение в
виде
Далее
решаем по дискриминанту.

Ответ: −24.

1. Задание 3

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

2. Задание 3

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

3. Задание 3

Решите уравнение .

4. Задание 3

Решите уравнение .

5. Задание 3

Решите уравнение .

6. Задание 3

Решите уравнение .

7. Задание 3

Решите уравнение .

8. Задание 3

Решите уравнение .

9. Задание 3

Решите уравнение .

10. Задание 3

Решите уравнение .

Задание 4

Найдите корни уравнения .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

Решение.

Решим уравнение:

Ответ: −0,20,2.

1. Задание 4

Найдите корни уравнения .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

2. Задание 4

Решите уравнение

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

3. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

4. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

5. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

6. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

7. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

8. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

9. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

10. Задание 4

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 5

Найдите корни уравнения .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

Решение.

Последовательно получаем:

Ответ: 05.

1. Задание 5

Найдите корни уравнения .

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

2. Задание 5

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

3. Задание 5

Найдите корни уравнения

Если корней несколько, запишите
их в ответ без пробелов в порядке возрастания.

4. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

5. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

6. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

7. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

8. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

9. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

10. Задание 5

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

Задание 6

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

Решение.

Запишем уравнение в виде:

Далее
решаем по дискриминанту.

Ответ: 14.

1. Задание 6

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

2. Задание 6

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания

3. Задание 6

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

4. Задание 6

Найдите корни уравнения

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

5. Задание 6

Найдите корни уравнения x²
+ 3x = 10.

Если корней несколько, запишите их в ответ без пробелов в
порядке возрастания.

6. Задание 6

Найдите корни уравнения

7. Задание 6

Найдите корни уравнения

8. Задание 6

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите больший из корней.

9. Задание 6

Решите уравнение Если
уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 7

Две
прямые пересекаются в точке C (см. рис.). Найдите
абсциссу точки C.

Решение.

Уравнения прямых:

Найдём абсциссу точки пересечения
прямых, для этого, приравняем ординаты:

Ответ: −2.

1. Задание 7

Две прямые пересекаются в точке C (см. рис.). Найдите
абсциссу точки C.

2. Задание 7

Две прямые пересекаются в точке C (см. рис.).
Найдите абсциссу точки C.

3. Задание 7

Две прямые пересекаются в точке C (см. рис.).
Найдите абсциссу точки C.

4. Задание 7

Две прямые пересекаются в точке C (см. рис.).
Найдите абсциссу точки C.

5. Задание 7

Две прямые пересекаются в точке C (см. рис.).
Найдите абсциссу точки C.

Задание 8

На
рисунке изображены графики функций и Вычислите
координаты точки B.

Запишите координаты в ответ без пробелов и знаков препинания.

Решение.

Точки A и B —
точки пересечения графиков функций и Найдём
их абсциссы:

Абсцисса точки B больше
нуля, следовательно, это Найдём
ординату точки B:

Ответ: 3−6.

1. Задание 8

На рисунке
изображены графики функций y = 6 − x² и y = − x.
Вычислите абсциссу точки B.

2. Задание 8

На рисунке
изображены графики функций y = 5 − x² и y = 4x.
Вычислите абсциссу точки B.

3. Задание 8

На рисунке изображены графики
функций и .
Вычислите абсциссу точки .

4. Задание 8

На рисунке изображены графики
функций и .
Вычислите абсциссу точки B.

5. Задание 8

На рисунке изображены графики
функций y=3− x 2 и y=2x . Вычислите координаты
точки B .

6. Задание 8

На рисунке изображены графики
функций y=2− x 2 и y=−x . Вычислите координаты
точки B .

7. Задание 8

На рисунке изображены графики
функций y=2− x 2 и y=x . Вычислите координаты
точки B .

8. Задание 8

На
рисунке изображены графики функций y = 6 − x² и y =
5x. Вычислите абсциссу точки B.

Задание 9

Квадратный трёхчлен разложен на множители: Найдите

Решение.

Корни уравнения
находим по дискриминанту. Это числа −9 и 3. По формуле  где  и  корни уравнения
получаем  Следовательно,

1. Задание
9

Квадратный трёхчлен разложен на множители: Найдите

2. Задание
9

Квадратный трёхчлен разложен на множители: Найдите a.

Задание
10

Решите уравнение

Решение.

Последовательно получаем:

Ответ: −9,7.

1. Задание 10

Решите уравнение

2. Задание 10

Решите уравнение

3. Задание 10

Решите уравнение

4. Задание 10

Решите уравнение

5. Задание 10

Решите уравнение

6. Задание 10

Решите уравнение

7. Задание 10

Решите уравнение

8. Задание 10

Решите уравнение

9. Задание 10

Решите уравнение

10. Задание 10

Решите уравнение

Задание 11

Решите уравнение

Решение.

Раскроем скобки и преобразуем выражение:

Ответ: 2,25.

1. Задание 11

Решите уравнение

2. Задание 11

Решите уравнение 10x² −
17x + 34 = 7x² − 26x + 28.

Если корней несколько, запишите их в ответ без пробелов в порядке
возрастания.

3. Задание 11

Решите уравнение

4. Задание 11

Решите уравнение

5. Задание 11

Решите уравнение

6. Задание 11

Решите уравнение

7. Задание 11

Решите уравнение

8. Задание 11

Решите уравнение

9. Задание 11

Решите уравнение

10. Задание 11

Решите уравнение

Задание 12

Решите уравнение

Решение.

Квадраты чисел равны, если числа равны или
противоположны:

Ответ: −2,5.

Приведем другое решение.

Раскроем скобки в обеих частях
уравнения:

Приведем другое решение.

Воспользуемся формулой разности
квадратов:

1. Задание 12

Решите уравнение (x − 9)² =
(x − 3)².

2. Задание 12

Решите уравнение

3. Задание 12

Решите уравнение

4. Задание 12

Решите уравнение

5. Задание 12

Решите уравнение

6. Задание 12

Решите уравнение

7. Задание 12

Решите уравнение

8. Задание 12

Решите уравнение

9. Задание 12

Решите уравнение

10. Задание 12

Решите уравнение

Задание 13

Уравнение имеет
корни −5; 7. Найдите

Решение.

По теореме Виета

Ответ: −35.

1. Задание 13

Уравнение имеет
корни −5; 2. Найдите

2. Задание 13

Уравнение имеет
корни −9; 1. Найдите

3. Задание 13

Уравнение имеет
корни 5; 9. Найдите

4. Задание 13

Уравнение имеет
корни −6; 1. Найдите

5. Задание 13

Уравнение имеет
корни −4; −1. Найдите

6. Задание 13

Уравнение имеет
корни −2; 1. Найдите

7. Задание 13

Уравнение имеет
корни −9; 6. Найдите

8. Задание 13

Уравнение имеет
корни −2; 7. Найдите

9. Задание 13

Уравнение имеет
корни 1; 6. Найдите

10. Задание 13

Уравнение имеет
корни −3; 3. Найдите

Источник

В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными.

Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию.

Ответом в задании №9 является целое число или конечная десятичная дробь.

Теория к заданию №9

Ниже я привел теорию по решениям линейных и квадратных уравнений:

Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи — в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем — решение полного квадратного уравнения с вычислением дискриминанта.

Разбор типовых вариантов задания №9 ОГЭ по математике

Первый вариант задания (линейные уравнения)

Найдите корень уравнения:

10 ( x — 9 ) = 7

Решение:

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x — 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

10x = 7 + 90

10x = 97

Затем делим обе части на 10:

x = 9,7

Ответ: 9,7

Второй вариант задания (неполные квадратные уравнения)

Решите уравнение:

3 x² + 12 x = 0

Решение:

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

x ( 3 x + 12 ) = 0

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

x = 0

или

3 x + 12 = 0

3 x = -12

x = -4

Так как в ответе просят указать наименьший корень, то это -4.

Ответ: -4

Третий вариант задания (квадратные уравнения)

Решите уравнение:

8 x² — 10x + 2 = 0

Решение:

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

4 x² — 5x + 1 = 0

Далее вычисляем дискриминант:

D = b² — 4ac

D = 5² — 4 •4•1 = 9

Вычисляем корни:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

Ответ: 0,25

Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)

Решите уравнение:

7х — 9 = 40

Решение:

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой — всё, что известно переносим в правую часть, всё, что неизвестно — оставляем в левой. Далее выполняем необходимое арифметическое действие.

Решение:

7х — 9 = 40

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

7х = 49

х в нашем случае — это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

х = 49/7, откуда

х = 7

Ответ: 7

Пятый вариант задания (рациональные уравнения)

Найдите корень уравнения:

Решение:

Прежде всего, исключим корень, который не входит в ОДЗ:

x+6≠0 → х≠–6

Далее решаем уравнение.

Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:

Применим правило пропорции. Перемножим между собой крайние ее члены и средние:

1·1=(х+6)·2

Выполним умножение в левой части уравнения и раскроем скобки справа:

1=2х+12

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

2х+12=1

Переносим 12 из левой части в правую:

2х=1–12

2х=–11

Находим корень:

х=–11/2=–5,5

ОДЗ это значение не исключает, поэтому оно является искомым результатом.

Ответ: –5,5

Шестой вариант задания(рациональные уравнения)

Найдите корень уравнения:

Решение:

Обе части уравнения приводим к единому знаменателю 12:

Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:

11х=44

х=44:11

х=4

Ответ: 4

Источник