Решу егэ 9 задание гипербола

Каталог заданий.
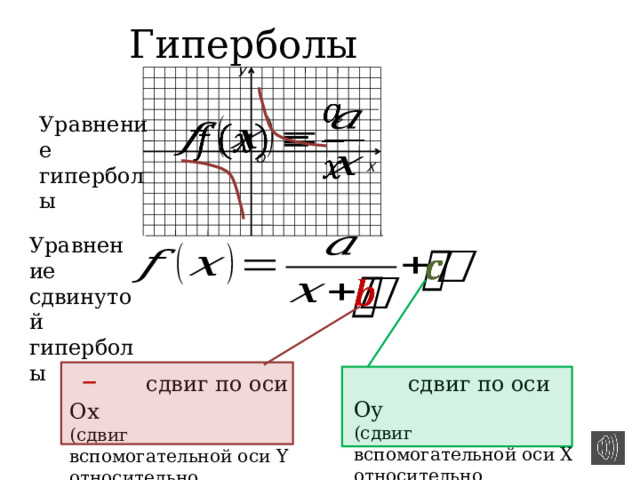
Гиперболы


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 10 № 508951

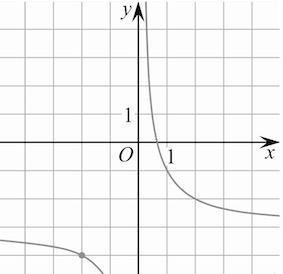
На рисунке изображён график функции f левая круглая скобка x правая круглая скобка =dfrackx плюс a. Найдите f левая круглая скобка минус 12 правая круглая скобка .

Аналоги к заданию № 508951: 508971 508952 508953 508954 508955 508956 508957 508958 508959 508960 … Все

Источник: А. Ларин: Тренировочный вариант № 110.

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

2

Тип 10 № 508961

На рисунке изображён график функции f левая круглая скобка x правая круглая скобка =dfrackx плюс a. Найдите, при каком значении x значение функции равно 0,8.

Аналоги к заданию № 508961: 508983 508962 508963 508964 508965 508966 508967 508968 508969 508970 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

3

Тип 10 № 564197

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: a, знаменатель: x плюс b конец дроби плюс c, где числа a, b и c  — целые. Найдите f левая круглая скобка 13 правая круглая скобка .

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

4

Тип 10 № 564198

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: a, знаменатель: x плюс b конец дроби плюс c, где числа a, b и c  — целые. Найдите f левая круглая скобка 9 правая круглая скобка .

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

5

Тип 10 № 564199

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: a, знаменатель: x плюс b конец дроби плюс c, где числа a, b и c  — целые. Найдите f левая круглая скобка минус 13 правая круглая скобка .

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник
Skip to content

ЕГЭ Профиль №9. Гипербола

ЕГЭ Профиль №9. Гиперболаadmin2022-08-17T23:36:10+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Гипербола

Задача 1. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)   Найдите  (fleft( { — 12} right).)

Ответ

ОТВЕТ: 0,75.
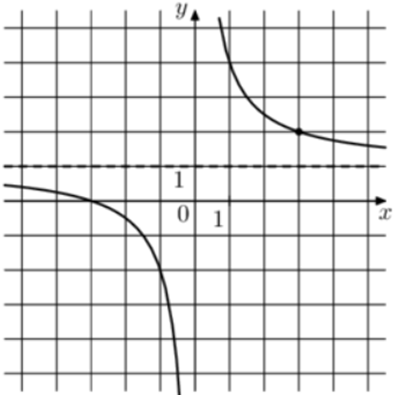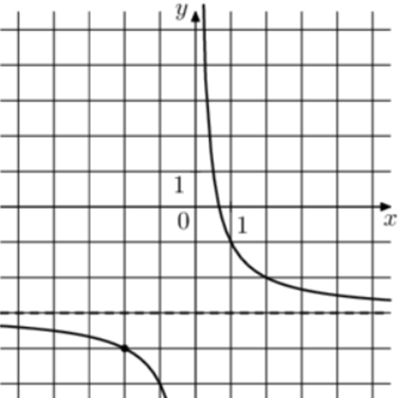
Задача 2. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {50} right).)

Ответ

ОТВЕТ: — 2,96.
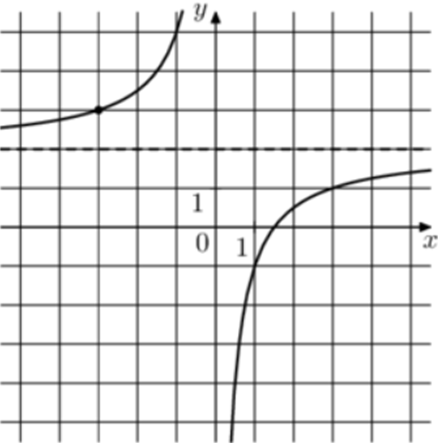
Задача 3. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {7,5} right).)

Ответ

ОТВЕТ: 1,6.
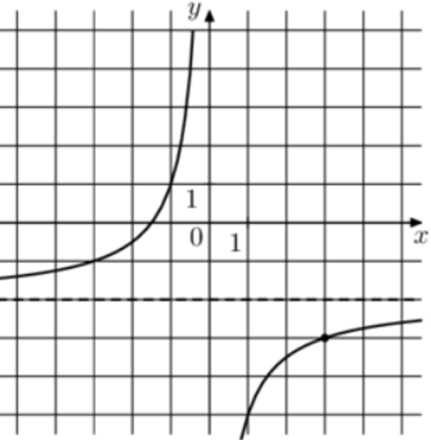
Задача 4. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {0,25} right).)

Ответ

ОТВЕТ: — 14.
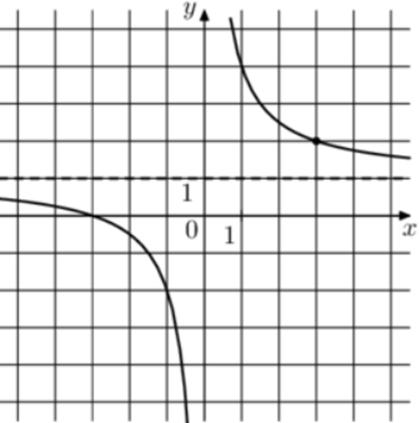
Задача 5. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 0,8.

Ответ

ОТВЕТ: — 15.
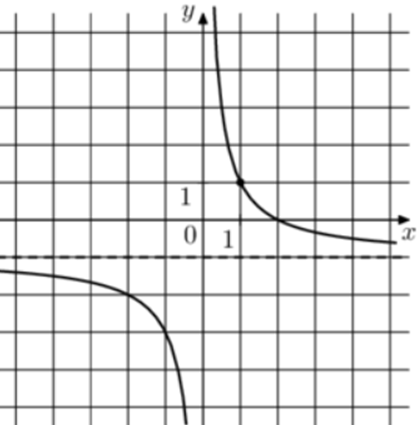
Задача 6. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 19.

Ответ

ОТВЕТ: 0,1.
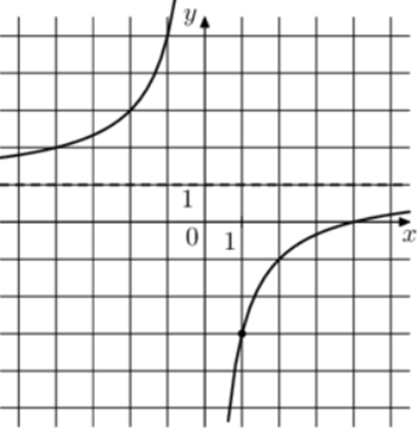
Задача 7. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 0,75.

Ответ

ОТВЕТ: 16.
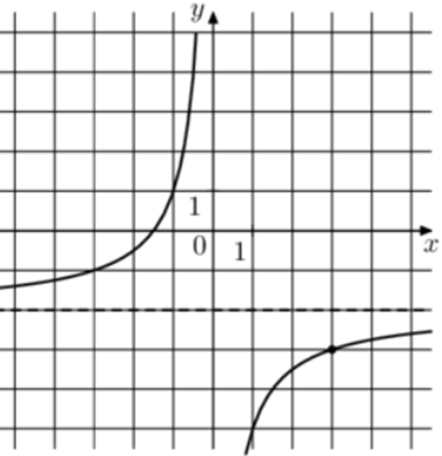
Задача 8. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно ( — 9,5.)

Ответ

ОТВЕТ: 0,4.
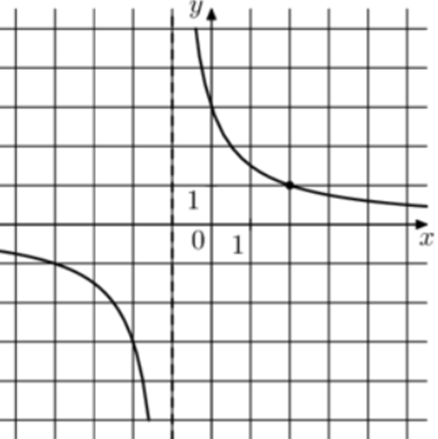
Задача 9. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {19} right).)

Ответ

ОТВЕТ: 0,15.
Задача 10. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( { — 4frac{2}{3}} right).)

Ответ

ОТВЕТ: — 0,75.
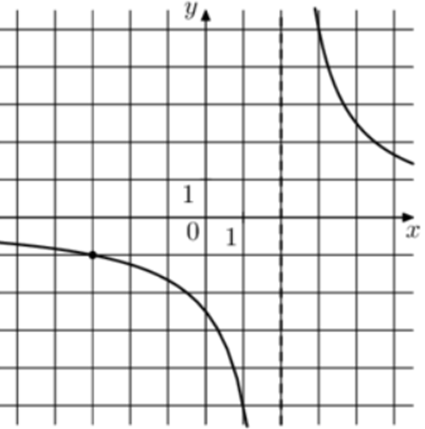Задача 11. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {18} right).)

Ответ

ОТВЕТ: — 0,1.
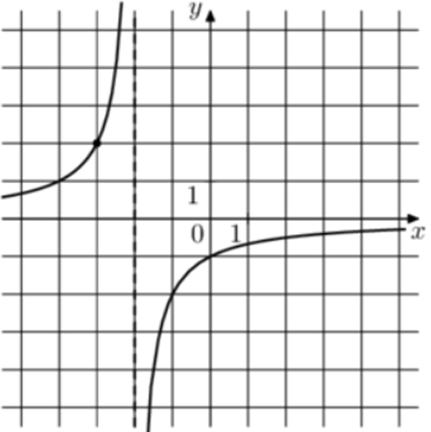Задача 12. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {6frac{1}{3}} right).)

Ответ

ОТВЕТ: — 0,24.
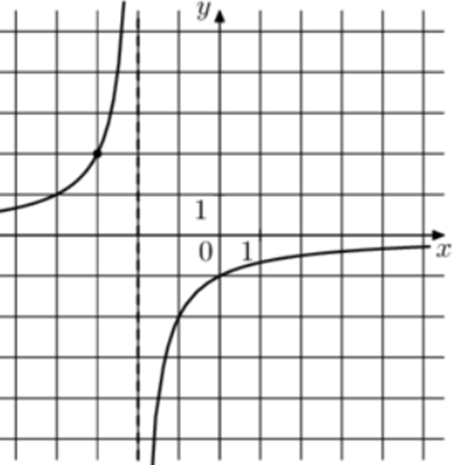Задача 13. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) = 0,2.)

Ответ

ОТВЕТ: 14.
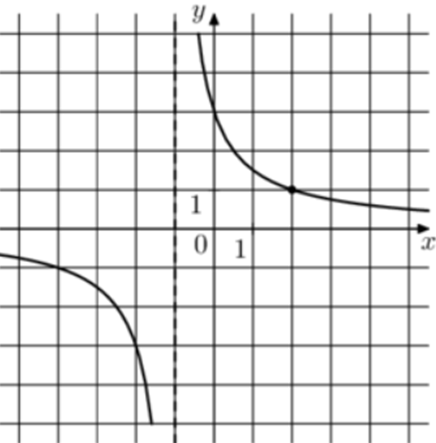Задача 14. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) =  — 0,08.)

Ответ

ОТВЕТ: — 24.
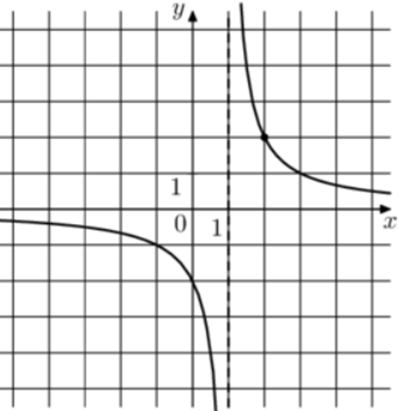Задача 15. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) =  — 0,04.)

Ответ

ОТВЕТ: 48.
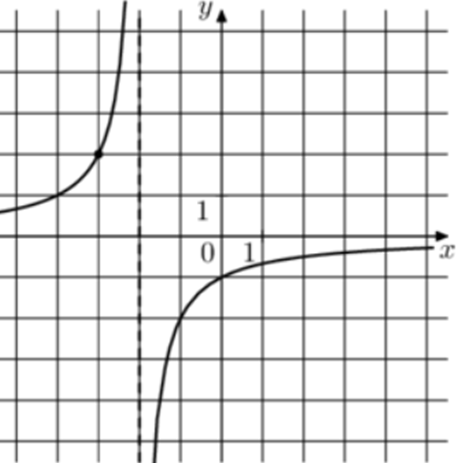Задача 16. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) = 0,2.)

Ответ

ОТВЕТ: — 29.
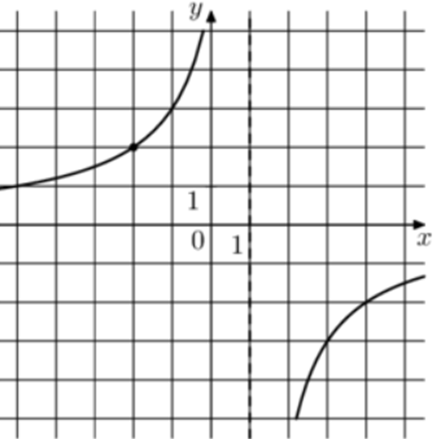Задача 17. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: 1.
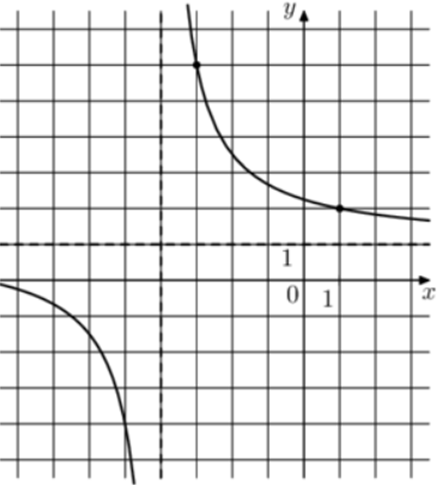Задача 18. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: 2.
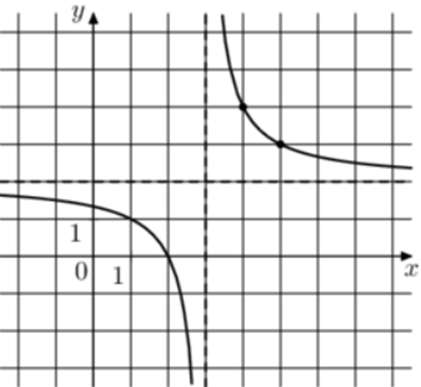Задача 19. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: 2.
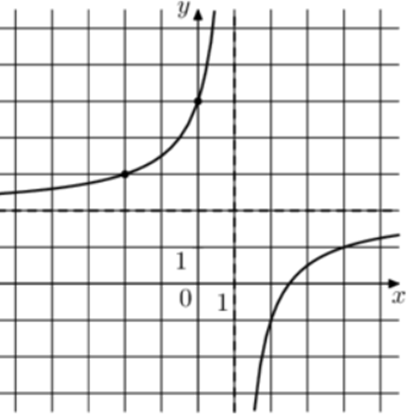Задача 20. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: — 2.
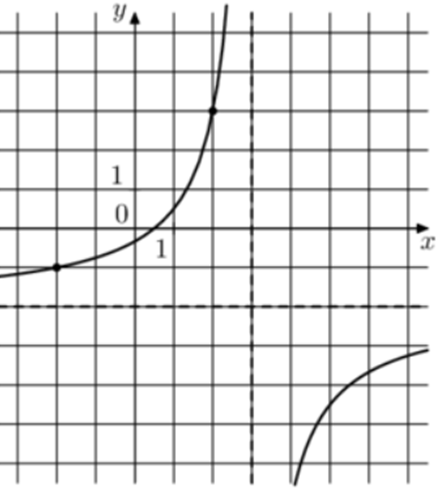Задача 21. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: 9.
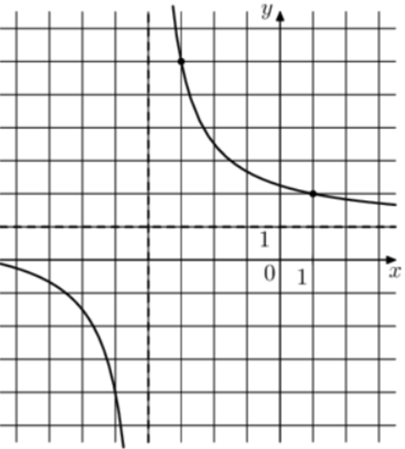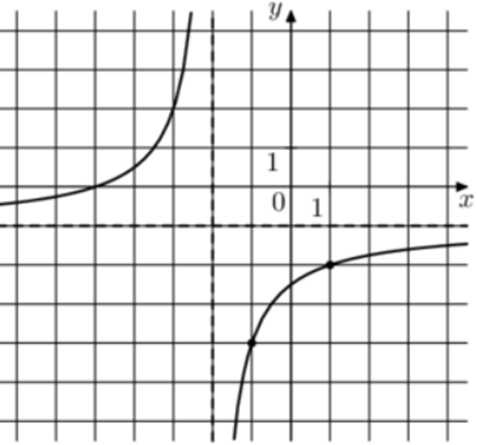
Задача 22. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: — 4.
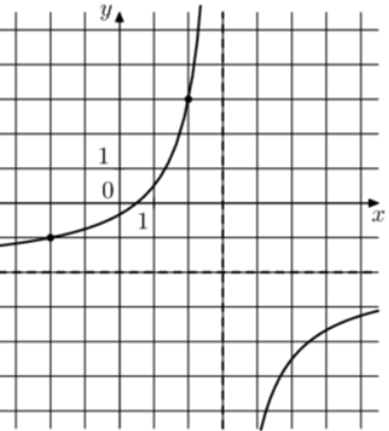
Задача 23. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: 1.
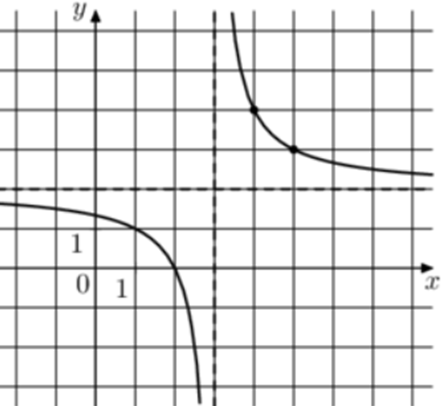
Задача 24. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: — 5.
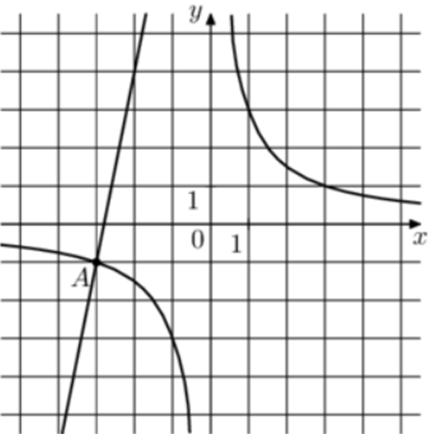
Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 0,2.
Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 6,25.
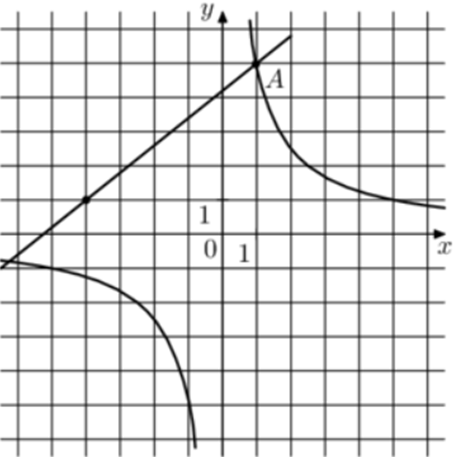Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 10.
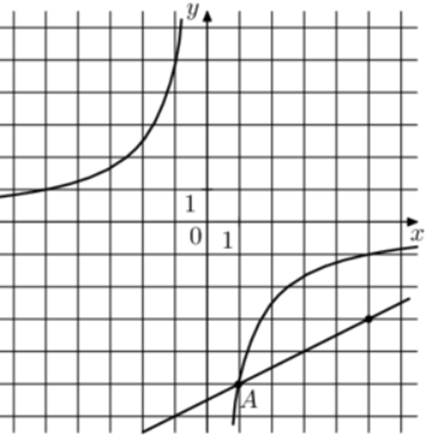Задача 28. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 12,5.
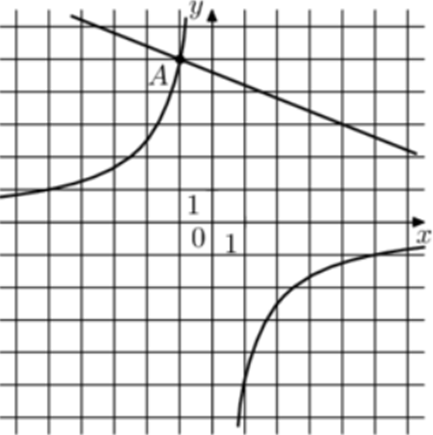Задача 29. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 15.
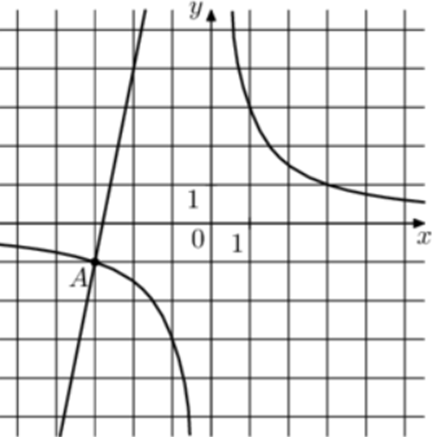Задача 30. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 16.
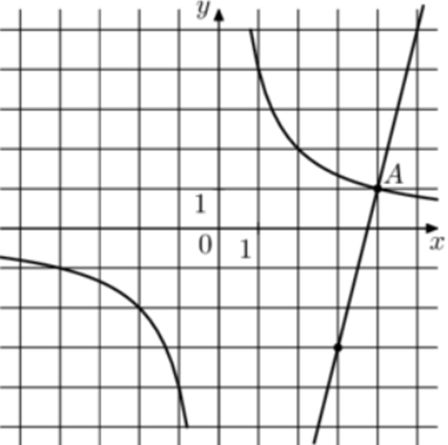Задача 31. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 0,4.
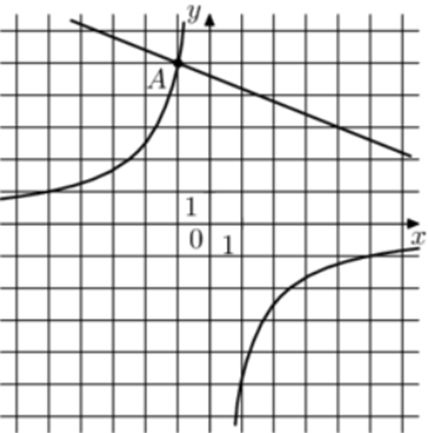Задача 32. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 0,5.

Источник

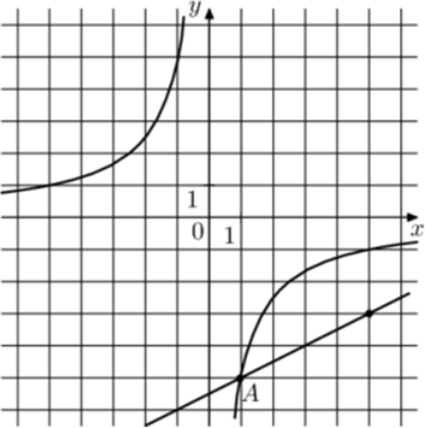09
Янв 2022

Категория: 10 Графики функций

2022-01-09
2022-09-11

Задача 1. На рисунке изображён график функции f(x)=frac{k}{x}+a.  Найдите f(50). 

Решение: + показать

Задача 2. На рисунке изображён график функции вида f(x)=frac{a}{x+b}+c,  где числа a,b и c — целые. Найдите значение x, при котором f(x)=2,5.

Решение: + показать

Задача 3. На рисунке изображён график функции  вида f(x)=frac{a}{x+b}+c, где a,b,c – целые числа.  Найдите f(frac{8}{3}).

Решение: + показать

Задача 4. На рисунке изображён график функции f(x)=frac{kx+a}{x+b}.  Найдите a.

Решение: + показать

Задача 5. На рисунке изображены графики функций f(x)=frac{k}{x}  и g(x)=ax+b и  которые пересекаются в точках A и B. Найдите ординату точки B.

Решение: + показать

Вы можете пройти тест “Гиперболы”

Автор: egeMax |

Нет комментариев

Источник

ЕГЭ 2022 ПРОФИЛЬНАЯ МАТЕМАТИКА РАЗБОР ЗАДАНИЯ №9
В этом уроке мы обсудим, как решать задание №9 на гиперболы.

Основные ссылки:
Группа Вконтакте: https://vk.com/path_in_math
Получать уведомления о вебинарах(рассылка Вконтакте): https://vk.com/app5898182_-199426423#…
Есть идеи или предложения? Связаться со мной можно по почте: pathmath2022@gmail.com
Или написать в сообщения группы Вконтакте: https://vk.com/path_in_math

Таймкоды:
00:00 кто убил path in math
01:15 стандартная гипербола
03:18 смещения гиперболы
08:16 практика по смещениям, строим гиперболу
13:44 решаем задание №9
18:28 как поддержать выход видеороликов
18:43 вопрос тысячелетия

Видео Задание №9 на ГИПЕРБОЛЫ. Подробный разбор. Профильная математика ЕГЭ 2022. канала PATH IN MATH: Математика — ЕГЭ, ОГЭ, ОЛИМПИАДЫ

Показать

ЕГЭ по математике профиль

Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.

Для успешного результата необходимо уметь выполнять действия с функциями.

Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы

Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:

3.3.1 Линейная функция, её график

3.3.2  Функция, описывающая обратную пропорциональную зависимость, её график

3.3.3 Квадратичная функция, её график

3.3.4 Степенная функция с натуральным показателем, её график

3.3.5 Тригонометрические функции, их графики

3.3.6 Показательная функция, её график

3.3.7 Логарифмическая функция, её график

Уметь выполнять действия с функциями:  определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:

При отработке данного задания будут полезны книги:

Графики функций ЕГЭ математика профиль

Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля

Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств

Связанные страницы:

верхняя шапка

картинка

MATHM
>>
ЕГЭ
>>
ЕГЭ профиль

>>

Задача 9

картинка

ЗАДАЧА 9
сортировка
по темам

СПИСОК ТЕМ

Тема 1: График параболы
Тема 2: График гиперболы и корня
Тема 3: График модуля
Тема 4: Графики тригонометрических функций
Тема 5: График показательной функции и логарифма
Тема 6: Пересечение графиков

Задачи разделены на темы. Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.

Тема 1: График параболы.

  1. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-12).

    2. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  2. На рисунке изображен график функции вида 𝑓𝑥=𝑎𝑥2+𝑏𝑥−𝑐, где числа 𝑎,𝑏 и 𝑐 – целые. Найдите 𝑓(6).

    3. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  3. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-8).

    4. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  4. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(18).

    5. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  5. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-16).

    6. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  6. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(8).

    7. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  7. На рисунке изображен график функции вида f(x)=〖a(x+1)〗^2+bx+c, где числа a,b и c – целые. Найдите f(-12).

    8. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  8. На рисунке изображен график функции вида f(x)=〖a(x-2)〗^2+b(x+1)+c, где числа a,b и c – целые. Найдите f(-15).

    9. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  9. На рисунке изображен график функции вида f(x)=〖a(x-4)〗^2+b(x+3)+c, где числа a,b и c – целые. Найдите f(-12).

    10. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  10. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-18).

    11. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  11. На рисунке изображен график функции вида f(x)=x^2/a+bx+c, где числа a,b и c – целые. Найдите f(-12).

    12. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  12. На рисунке изображен график функции вида 𝑓𝑥=𝑥2𝑎+𝑏𝑥+𝑐, где числа 𝑎,𝑏 и 𝑐 – целые. Найдите 𝑓(20).

    13. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

Тема 2: График гиперболы и корня.

  1. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(-14).

    2. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  2. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(12).

    3. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  3. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(15).

    4. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  4. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(20).

    5. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  5. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(160).

    6. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  6. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(399).

    7. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  7. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(-1056).

    8. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  8. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(-895).

    9. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  9. На рисунке изображен график функции вида f(x)=-√(ax+b)+c, где числа a,b и c – целые. Найдите f(-1056).

    10. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  10. На рисунке изображен график функции вида f(x)=-√(ax+b)+c, где числа a,b и c – целые. Найдите f(720).

    11. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

Тема 3: График модуля.

  1. На рисунке изображен график функции вида f(x)=|ax+b|+c, где числа a,b и c – целые. Найдите f(88).

    2. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

  2. На рисунке изображен график функции вида f(x)=|ax+b|+c, где числа a,b и c – целые. Найдите f(-56).

    3. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

  3. На рисунке изображен график функции вида f(x)=-|ax+b|+c, где числа a,b и c – целые. Найдите f(81).

    4. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

  4. На рисунке изображен график функции вида f(x)=-|ax+b|+c, где числа a,b и c – целые. Найдите f(-23).

    5. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

Тема 4: Графики тригонометрических функций.

  1. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(10/3).

    2. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  2. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(-11/3).

    3. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  3. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(19/3).

    4. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  4. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(-22/3).

    5. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  5. На рисунке изображен график функции вида f(x)=〖a∙sin〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(23/6).

    6. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  6. На рисунке изображен график функции вида f(x)=〖a∙sin〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(23/6).

    7. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

Тема 5: График показательной функции и логарифма.

  1. На рисунке изображен график функции вида f(x)=2^(ax+b)+c, где числа a,b и c – целые. Найдите f(4).

    2. посмотреть ответ

    посмотреть решение

  2. На рисунке изображен график функции вида f(x)=3^(ax+b)+c, где числа a,b и c – целые. Найдите f(3).

    3. посмотреть ответ

    посмотреть решение

  3. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(510).

    4. посмотреть ответ

    посмотреть решение

  4. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(257).

    5. посмотреть ответ

    посмотреть решение

  5. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(244).

    6. посмотреть ответ

    посмотреть решение

  6. На рисунке изображен график функции вида f(x)=log_4⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(65).

    7. посмотреть ответ

    посмотреть решение

  7. На рисунке изображен график функции вида f(x)=log_2⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-130).

    8. посмотреть ответ

    посмотреть решение

  8. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-84).

    9. посмотреть ответ

    посмотреть решение

Тема 6: Пересечение графиков.

  1. На рисунке изображен график функции вида f(x)=2^(ax+b)+c, где числа a,b и c – целые. Найдите f(4).

    2. посмотреть ответ

    посмотреть решение

  2. На рисунке изображен график функции вида f(x)=3^(ax+b)+c, где числа a,b и c – целые. Найдите f(3).

    3. посмотреть ответ

    посмотреть решение

  3. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(510).

    4. посмотреть ответ

    посмотреть решение

  4. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(257).

    5. посмотреть ответ

    посмотреть решение

  5. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(244).

    6. посмотреть ответ

    посмотреть решение

  6. На рисунке изображен график функции вида f(x)=log_4⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(65).

    7. посмотреть ответ

    посмотреть решение

  7. На рисунке изображен график функции вида f(x)=log_2⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-130).

    8. посмотреть ответ

    посмотреть решение

  8. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-84).

    9. посмотреть ответ

    посмотреть решение

  9. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-84).

    10. посмотреть ответ

    посмотреть решение

нижняя шапка

29 декабря 2021

В закладки

Обсудить

Жалоба

В версии ЕГЭ-2022 по математике появилось новое 9 задание, в котором требуется работа с функциями.

Эта тема пока вызывает затруднения у учащихся в связи со своей новизной. В презентации представлены решения задач с использованием линейной и квадратичной функций. Некоторые задачи решены 3 способами, чтобы учащиеся смогли выбрать наиболее понятный для себя.

ege9new.pptx
ege9new.pdf

Автор: Лесных Марина Владимировна.

Тест «Витамины»

Проверочная работа по биологии в 8 классе.

Консультация по физике

Онлайн-трансляция по вопросам подготовки к ЕГЭ по физике.

Sorry, your request has been denied.

Источник

Решу ЕГЭ 2022 задание №9 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки к экзамену.

  • скачать задания прямая с ответами
  • скачать задания парабола с ответами
  • скачать задания гипербола с ответами
  • скачать задания логарифмические функции с ответами
  • скачать задания иррациональные функции с ответами
  • скачать задания тригонометрические функции с ответами

Решу ЕГЭ 2022 линейные функции 9 задание математика с ответами:

Решу ЕГЭ 2022 парабола 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 гипербола 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 логарифмические функции 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 иррациональные функции 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 тригонометрические функции 9 задание профиль математика с ответами:

Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Как решать 9 задание ЕГЭ 2022 математика профиль видео теория:



1)На рисунке изображён график функции вида f(x)= a3x+b x+c , где числа a, b и c — целые. Найдите a.

2)На рисунке изображён график функции вида f(x)= 2ax+b x+c , где числа a, b и c — целые. Найдите a.

3)На рисунке изображён график функции вида f(x)= ax+b x+c , где числа a, b и c — целые. Найдите a.

4)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(−22).

5)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите решение уравнения f(x)=18.

6)На рисунке изображён график функции вида f(x)= 2ax+b x+c , где числа a, b и c — целые. Найдите a.

7)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(15).

8)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.

9)На рисунке изображён график функции вида f(x)=log5(ax+b)+c, где числа a, b, c  — целые. Найдите наибольшее значение функции g(x)=−x2+ax+b.

10)На рисунке изображён график функции вида f(x)=log1.4(x−a)+b, где числа a, b  — целые. Найдите ab.

11)На рисунке изображён график функции вида f(x)=2ax+b, где числа a, b  — целые. Найдите сумму коэффициентов a+b, если f(1)=10.

12)На рисунке изображён график функции вида f(x)=log2(ax+b)+2, где числа a, b  — целые. Найдите сумму коэффициентов a+b.

13)На рисунке изображён график функции вида f(x)=ln(a+x)+b, где числа a, b  — целые. Найдите сумму коэффициентов a+b, если A(0;ln2e).

Задание №3 ЕГЭ 2022 по математике профиль прототипы с ответами

Задание №4 ЕГЭ 2022 по математике профиль прототипы с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

  • Cайты учителей
  • Все блоги
  • Все файлы
  • Все тесты
  • Мои уведомления
    1

  • Войти
  • Зарегистрироваться / Создать сайт

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 31.01.2022 15:49

Бабошкина Любовь Юрьевна

Учитель математики

66 лет

рейтинг1 728
место23 187

09.11.2021 20:48

Нажмите, чтобы узнать подробности

В презентации разбирается один из способов решения задания №9 ЕГЭ (гиперболы)

Просмотр содержимого документа

«Графики функции. Задание №9 ЕГЭ-2022»

Графики функций Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

Графики функций

Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

Гиперболы У   Уравнение гиперболы О Х   Уравнение сдвинутой гиперболы     – сдвиг по оси Ох (сдвиг вспомогательной оси Y относительно основной) сдвиг по оси Оу (сдвиг вспомогательной оси Х относительно основной)

Гиперболы

У

Уравнение гиперболы

О

Х

Уравнение

сдвинутой

гиперболы

– сдвиг по оси Ох

(сдвиг вспомогательной оси Y относительно основной)

сдвиг по оси Оу

(сдвиг вспомогательной оси Х относительно основной)

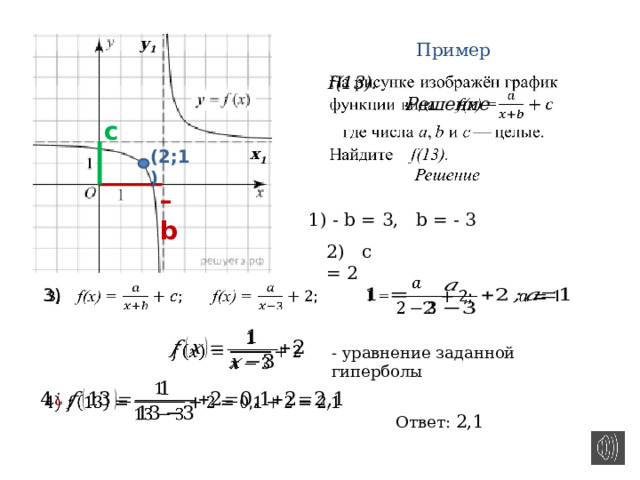
y 1 Пример   f(13). Решение c x 1 (2;1) – b 1) - b = 3, b = - 3 2) c = 2   3)     - уравнение заданной гиперболы   Ответ: 2,1

y 1

Пример

f(13).

Решение

c

x 1

(2;1)

– b

1) — b = 3, b = — 3

2) c = 2

3)

— уравнение заданной гиперболы

Ответ: 2,1

Рекомендуем курсы ПК и ППК для учителей

Похожие файлы

Источник

Понравилась статья? Поделить с друзьями:
  • Решу егэ 77336
  • Решу егэ 89983
  • Решу егэ 77333
  • Решу егэ 8932
  • Решу егэ 8664 информатика