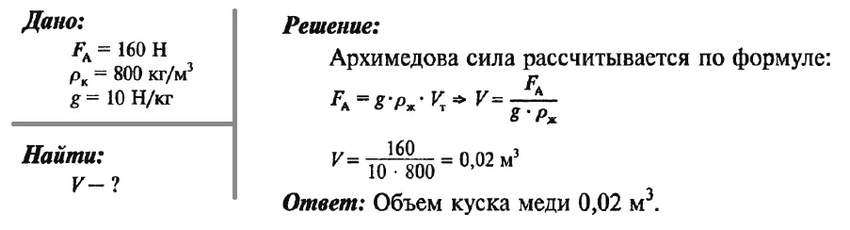Решу егэ архимедова сила - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На графике показана зависимость модуля силы Архимеда F_Арх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в килограммах на кубический метр. Ускорение свободного падения принять равным 10 м/с².

В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см.

В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с².

Кубик из пробки с ребром 10 см опускают в воду. Каково отношение объёма кубика, находящегося над водой, к объёму кубика, находящегося под водой? Плотность пробки 0,25 г/см³.

Пустой цилиндрический стеклянный стакан плавает в воде, погрузившись на половину своей высоты. Дно стакана при плавании горизонтально, плотность стекла 2500 кг/м³. Чему равно отношение внутреннего объёма стакана к его наружному объёму? Ответ представьте в виде десятичной дроби, округлив до десятых долей.

Пройти тестирование по этим заданиям

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 100 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

К концам лёгкого стержня длиной l, лежащего на клиновидной опоре, установленной на расстоянии от его левого конца, подвешены на невесомых нитях два тяжёлых груза 1 и 2 с плотностями rho_1 (слева) и rho_2 (справа). Стержень находится в равновесии в горизонтальном положении (см. рис.).

Затем, опустив точку опоры стержня, грузы полностью погрузили в стаканы с жидкостями  — водой слева и керосином справа, и при этом равновесие стержня сохранилось. Чему равно отношение плотностей грузов Какие законы Вы использовали для решения этой задачи? Обоснуйте их применимость к данному случаю.

Затем, опустив точку опоры стержня, грузы полностью погрузили в стаканы с жидкостями  — керосином слева и водой справа, опустив точку опоры стержня, и при этом его равновесие сохранилось. Чему равно отношение плотностей грузов Какие законы Вы использовали для решения этой задачи? Обоснуйте их применимость к данному случаю.

На кусок алюминия массой 0,54 кг при полном погружении в воду действует сила Архимеда, равная 2 Н. Чему равна при этом масса вытесненной воды? Ответ дайте в килограммах.

Источник: ЕГЭ по физике 2021. Досрочная волна. Вариант 1

Сейчас люди на праздники стали часто запускать в небо китайские фонарики, представляющие собой лёгкие бумажные мешки с отверстием внизу, в котором на проволочном каркасе крепится кусок пористого материала, пропитанного горючим. После его поджигания фонарик поднимается в небо на большую высоту, а потом может приземлиться вдали от точки старта. В городе, в лесу и при сильном ветре запускать фонарики опасно!

Опишите, основываясь на известных физических законах и закономерностях, процессы, происходящие в течение всех фаз полёта такого фонарика. В чём причина опасности, о которой говорилось выше?

В наше время на дни рождения часто дарят резиновые шарики, надутые гелием,  — они не взрывоопасны и имеют довольно большую подъёмную силу. Объясните, основываясь на известных физических законах и закономерностях, происхождение этой подъёмной силы и определите, на сколько она изменится, если вместо гирлянды из 27 шаров, в каждый из которых накачали по 1 молю гелия, надуть тем же количеством гелия один большой шар? Толщина резиновой оболочки у всех шаров одинакова, давление и температура близки к нормальным, а подъёмная сила гирлянды равна 1,52 Н.

В наше время на дни рождения часто дарят резиновые шарики, надутые гелием, – они не взрывоопасны и имеют довольно большую подъёмную силу. Объясните, основываясь на известных физических законах и закономерностях, происхождение этой подъёмной силы и определите, на сколько она изменится, если вместо гирлянды из 8 шаров, в каждый из которых накачали по 1 молю гелия, надуть тем же количеством гелия один большой шар? Толщина резиновой оболочки у всех шаров одинакова, давление и температура близки к нормальным, а подъёмная сила гирлянды равна 0,45 Н.

К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см³, плотность жидкости 800 кг/м³, объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.

1)  Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.

2)  Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.

3)  Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.

4)  Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.

5)  Объём погружённой части тела равен четверти объёма этого тела.

1)  Модуль силы Архимеда, действующей на тело, больше модуля силы Архимеда, действующей на шарик.

2)  Модуль силы натяжения нити меньше модуля силы тяжести, действующей на шарик.

3)  Модуль силы натяжения нити равен модулю силы тяжести, действующей на тело.

4)  Модуль силы тяжести, действующей на шарик, меньше модуля силы тяжести, действующей на тело.

5)  Объём погружённой части тела равен 3/4 объёма этого тела.

Тонкий однородный стержень, частично погружённый в воду, удерживается в состоянии равновесия с помощью невесомой нерастяжимой нити (см. рис.). Длина отрезка АВ в два раза меньше длины отрезка ОА.

Выберите все верные утверждения.

1)  Модуль силы натяжения нити меньше модуля действующей на стержень силы тяжести.

2)  Сумма модулей силы натяжения нити и силы Архимеда больше модуля действующей на стержень силы тяжести.

3)  Относительно оси, проходящей через точку О, плечо действующей на стержень силы тяжести меньше плеча силы Архимеда.

4)  Относительно оси, проходящей через точку О, отношение плеча действующей на стержень силы Архимеда к плечу силы натяжения нити равно 1,2.

5)  Относительно оси, проходящей через точку О, момент силы Архимеда больше момента действующей на стержень силы тяжести.

Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рис.). Из приведённого ниже списка выберите все правильные утверждения.

1)  Плотность материала, из которого изготовлены бруски, равна 500 кг/м³.

2)  Если на верхний брусок положить груз массой 0,7 кг, то бруски утонут.

3)  Если воду заменить на керосин, то глубина погружения брусков уменьшится.

4)  Сила Архимеда, действующая на бруски, равна 20 Н.

5)  Если в стопку добавить ещё два таких же бруска, то глубина её погружения увеличится на 10 см.

Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 1

1)  Если воду заменить на подсолнечное масло, то глубина погружения брусков уменьшится.

2)  Если на верхний брусок поставить гирю массой 1,5 кг, то бруски не утонут.

3)  Если в стопку добавить ещё три таких же бруска, то глубина её погружения увеличится на 15 см.

4)  Сила Архимеда, действующая на бруски, равна 10 Н.

5)  Плотность материала, из которого изготовлены бруски, равна 500 кг/м³.

Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 2

На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Глубина погружения бруска	Сила Архимеда

Источник: Демонстрационная версия ЕГЭ—2016 по физике.

Прямоугольный сплошной параллелепипед ABCDMFEK, длины рёбер которого относятся как 3 : 2 : 1, изготовлен из некоторого материала. Если аккуратно опустить параллелепипед в жидкость так, как показано на рисунке 1, то он будет плавать так, что его нижняя грань будет погружена на глубину

Как изменятся модуль силы Архимеда, действующей на параллелепипед, и глубина погружения нижней грани параллелепипеда, если его аккуратно опустить в эту же жидкость, повернув так, как показано на рисунке 2?

Для каждой величины определите соответствующий характер её изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

Модуль силы Архимеда,

действующей на

параллелепипед

Глубина погружения

нижней грани

параллелепипеда

Как изменятся глубина погружения нижней грани параллелепипеда и модуль силы Архимеда, действующей на параллелепипед, если его аккуратно опустить в эту же жидкость, повернув на 90 градусов так, как показано на рисунке 2?

Для каждой величины определите соответствующий характер её изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Глубина погружения

нижней грани

параллелепипеда

Модуль силы Архимеда,

действующей на

параллелепипед

Деревянный кубик с ребром 10 см плавает частично погруженный в воду. Его начинают медленно погружать, действуя силой, направленной вертикально вниз. В таблице приведены значения модуля силы, под действием которой кубик находится в равновесии частично или полностью погруженный в воду. Выберите все верные утверждения на основании данных, приведенных в таблице.

№ опыта	1	2	3	4	5	6	7	8
Модуль силы, F, H	0,2	0,8	1,8	3,0	4,0	5,0	6,0	6,0

1)  В опыте № 8 сила Архимеда, действующая на кубик, больше, чем в опыте № 7.

2)  В опыте № 5 кубик погружен в воду полностью.

3)  Масса кубика равна 0,5 кг.

4)  При выполнении опытов № 1  — № 5 сила Архимеда, действующая на тело, увеличивалась.

5)  Плотность кубика равна 400 кг/м³.

Тело массой 600 г плавает в очень глубоком сосуде на поверхности жидкости, погрузившись в неё на 3/4 своего объёма. К телу прикладывают направленную вертикально вниз силу, модуль которой равен 3 Н. Чему через достаточно большое время после этого станет равен модуль силы Архимеда, действующей на тело?

Тело массой 800 г плавает в очень глубоком сосуде на поверхности жидкости, погрузившись в неё на 2/3 своего объёма. К телу прикладывают направленную вертикально вниз силу, модуль которой равен 5 Н. Чему через достаточно большое время после этого станет равен модуль силы Архимеда, действующей на тело?

Наполненная газом сферическая резиновая оболочка полностью погружена в глубокий водоём и имеет радиус 75 см. Оболочку начинают погружать вглубь водоёма, и через некоторое время её радиус становится равным 25 см (а форма остаётся сферической). Во сколько раз в результате такого погружения изменяется модуль действующей на оболочку силы Архимеда? Считайте изменение плотности воды с увеличением глубины пренебрежимо малым.

Наполненная газом сферическая резиновая оболочка полностью погружена в глубокий водоём и имеет радиус 15 см. Оболочку начинают поднимать к поверхности водоёма, и через некоторое время её радиус становится равным 60 см (а форма остаётся сферической). При этом оболочка по-прежнему остаётся полностью погруженной в воду. Во сколько раз в результате такого подъёма изменяется модуль действующей на оболочку силы Архимеда? Считайте изменение плотности воды с уменьшением глубины пренебрежимо малым.

На поверхности воды плавает прямоугольный брусок из древесины плотностью 400 кг/м³. Брусок заменили на другой брусок той же массы и с той же площадью основания, но из древесины плотностью 600 кг/м³. Как при этом изменились глубина погружения бруска и действующая на него сила Архимеда?

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Глубина погружения

бруска

Сила Архимеда

Источник: Демонстрационная версия ЕГЭ—2022 по физике

Всего: 100 1–20 | 21–40 | 41–60 | 61–80 …

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 82 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Глубина погружения

бруска

Сила Архимеда

Источник: Демонстрационная версия ЕГЭ—2022 по физике

Полый стальной шар массой 8 кг плавает на поверхности озера. Объем шара равен 16 дм³. Чему равна сила Архимеда, действующая на шар. Ответ дайте в ньютонах.

На плавающем в воде теле объёмом 800 см³ стоит кубик массой 300 г. При этом тело погружено в воду целиком, а кубик весь находится над водой. Чему станет равным объём погружённой в воду части тела, если снять с него кубик? В обоих случаях плавание тела является установившимся. Ответ выразите в кубических сантиметрах и округлите до целого числа.

Для выполнения лабораторной работы ученику выдали динамометр, груз неизвестной плотности и мензурку с водой. К сожалению, на динамометре не была указана цена деления шкалы. Используя зарисовки хода эксперимента, определите цену деления шкалы динамометра. (Ответ дать в ньютонах.)

В сосуд налито 4 л жидкости плотностью 1300 кг/м³. В этой жидкости в равновесии плавает тело, объём погружённой части которого равен 240 см³. В сосуд доливают ещё 4 л жидкости плотностью 1100 кг/м³ и перемешивают их. Чему после этого будет равен объём погружённой части тела в см³ при плавании в равновесии, если известно, что тело продолжает плавать? В обоих случаях плавающее тело не касается стенок и дна сосуда. Обе жидкости хорошо смешиваются, и при смешивании их суммарный объём сохраняется.

Жидкость	Бензин	Спирт	Вода	Глицерин	Хлороформ	Бромоформ	Дийодметан
г/см³	0,71	0,79	1,0	1,26	1,49	2,89	3,25

Ученик помещал цилиндр объемом V  =  10 см³, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погружённой в жидкость части цилиндра V_погр. По результатам измерений была получена зависимость объема погружённой части цилиндра V_погр от плотности жидкости rho (см. рис.).

Выберите все верные утверждения, согласующиеся с данными, представленными на рисунке и в таблице.

1)  В бензине и спирте сила Архимеда, действующая на цилиндр, одинакова.

2)  Цилиндр тонет в спирте.

3)  На цилиндр, плавающий в хлороформе, действует выталкивающая сила 0,1 Н.

4)  Цилиндр плавает во всех жидкостях, указанных в таблице.

5)  При плавании цилиндра в бромоформе и дийодметане сила Архимеда, действующая на цилиндр, одинакова.

В сосуд налито 3 л воды. В этой воде в равновесии плавает тело, объём погружённой части которого равен 110 см³. В сосуд доливают ещё 3 л жидкости плотностью 1200 кг/м³ и перемешивают их. Чему после этого будет равен объём погружённой части тела (в см³) при плавании в равновесии? В обоих случаях плавающее тело не касается стенок и дна сосуда. Обе жидкости хорошо смешиваются, и при смешивании их суммарный объём сохраняется.

Выберите все верные утверждения.

1)  Модуль силы натяжения нити меньше модуля действующей на стержень силы тяжести.

2)  Сумма модулей силы натяжения нити и силы Архимеда больше модуля действующей на стержень силы тяжести.

Тело, изготовленное из сосны, плавает в воде, погрузившись в неё на 20% от своего полного объёма. Из приведённого ниже списка выберите все верные утверждения. Запишите цифры, под которыми они указаны.

1)  Плотность воды больше средней плотности тела.

2)  Внутри тела есть полости, заполненные материалом, средняя плотность которого больше плотности сосны.

3)  Внутри тела есть полости, заполненные материалом, средняя плотность которого меньше плотности сосны (либо пустые).

4)  Внутри тела нет полостей.

5)  Средняя плотность тела равна 200 кг/м³.

Тело, изготовленное из сосны, плавает в керосине, погрузившись в него на 30% от своего полного объёма. Из приведённого ниже списка выберите все верные утверждения. Запишите цифры, под которыми они указаны.

1)  Внутри тела есть полости, заполненные материалом, средняя плотность которого меньше плотности сосны (либо пустые).

2)  Внутри тела есть полости, заполненные материалом, средняя плотность которого больше плотности керосина.

3)  Внутри тела нет полостей.

4)  Данное тело будет плавать в воде.

5)  Средняя плотность тела равна 240 кг/м³.

Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.

Какие две установки следует использовать для проведения такого исследования?

Источник: Демонстрационная версия ЕГЭ−2019 по физике

На плавающем в воде теле объёмом 500 см³ стоит кубик массой 100 г. При этом тело погружено в воду целиком, а кубик весь находится над водой. Чему станет равным объём погружённой в воду части тела, если снять с него кубик? В обоих случаях плавание тела является установившимся. Ответ выразите в кубических сантиметрах и округлите до целого числа.

Источник: ЕГЭ по физике 2021. Досрочная волна. Вариант 1

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Глубина погружения бруска	Сила Архимеда

Источник: Демонстрационная версия ЕГЭ—2016 по физике.

В сосуде с водой, не касаясь стенок и дна, плавает деревянный (сосновый) кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? Ответ выразите в ньютонах. (Плотность сосны  — 400 кг/м³.)

1)  Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.

2)  Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.

3)  Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.

4)  Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.

5)  Объём погружённой части тела равен четверти объёма этого тела.

Тело массой m и объёмом V плавает, частично погрузившись в жидкость плотностью ρ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А)  Модуль действующей на тело силы Архимеда

Б)  Объём погружённой части тела

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Всего: 82 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Сила Архимеда

Из кодификатора по физике, 2020.

«1.3.5. … если тело и жидкость покоятся в ИСО, то

Теория

Архимедова (выталкивающая) сила равна:

где – плотность жидкости (кг/м³), g — ускорение свободного падения (м/с²),

— объем погруженной части тела (м³).

— Объем жидкости , вытесненной телом, равен объему погруженной части тела в жидкость

— Если тело находится полностью в жидкости, то объем жидкости , вытесненной телом, равен объему тела

Задачи

Задача 1. Груз массой 3 кг, подвешенный на тонкой нити, целиком по-гружен в воду и не касается дна сосуда (рис. 1). Модуль силы натяжения нити 10 Н. Найдите объём груза (в литрах).

Решение. На груз в воде действуют сила тяжести ( mcdot g ), архимедова сила (F_A) и сила натяжения нити (Т). Ось OY направим вверх (рис. 2). Запишем второй закон Ньютона:

где — плотность воды, которую находим из таблицы «Плотность» (см. «Справочные данные»). Тогда

Задача 2. Предмет из алюминия объемом 100 см³ подвесили к пружине и опустили в бензин. Определите силу натяжения пружины.

Решение. На тело в керосине действуют сила тяжести ( mcdot g ), архимедова сила (F_A) и сила упругости (F_упр) пружины. Ось OY направим вверх (рис. 3). Запишем второй закон Ньютона:

где — объем тела, — масса тела,

=700 кг/м³ — плотность бензина, ρ = 2700 кг/м³ — плотность алюминия, которые находим из таблицы «Плотность» (см. «Справочные данные»). Тогда

Задача 3. Стальной шарик висит на нити, привязанной к штативу. Шарик целиком погружен в керосин (рис. 4). Затем стакан с керосином заменили на стакан с водой, и шарик оказался целиком в воде (рис. 5). Как изменились при этом сила натяжения нити и сила Архимеда, действующая на шарик?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась; 2) уменьшилась; 3) не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Сила натяжения нити	Сила Архимеда, действующая на шарик

Решение. На тело в жидкости действуют сила тяжести ( mcdot g ), архимедова сила (F_A) и сила натяжения нити (T). Ось OY направим вверх (рис. 6). Запишем второй закон Ньютона:

Архимедова сила равна

где — объем тела. Тогда

Масса бруска m и его объем V не меняются, плотность жидкости ρ_ж увеличивается (ρ_1ж = 800 кг/м3 — плотность керосина, ρ_2ж = 1000 кг/м3 — плотность воды, которые находим из таблицы «Плотность» (см. «Справочные данные»)).

Из уравнения (2) следует, что так как масса бруска m не меняется, а плотность жидкости ρ_жувеличивается, то сила натяжения нити уменьшается. Это соответствует изменению № 2.

Из уравнения (1) следует, что так как масса бруска m и его объем V не меняются, а плотность жидкости ρ_ж увеличивается, то сила Архимеда так же увеличивается. Это соответствует изменению № 1.

Ответ: 21.

Задача 4. К динамометру подвесили тело. Показания динамометра в воздухе 12 Н, в воде — 7 Н. Определите плотность тела.

Решение. Показания динамометра — это значение силы упругости F_упр его пружины. На тело в воздухе действуют сила тяжести ( mcdot g ) и сила упругости (F_упр1) (рис. 7, а). На тело в воде действуют сила тяжести ( mcdot g ), архимедова сила (F_A) и сила упругости (F_упр2) (рис. 7, б). Ось 0Y направим вверх. Запишем второй закон Ньютона для двух случаев:

где — объем тела, ρ_ж = 1000 кг/м³ — плотность воды, которую находим из таблицы «Плотность» (см. «Справочные данные»), ρ — плотность тела. Тогда

Автор Сакович А.Л.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Сила Архимеда» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Задачи на силу Архимеда с решениями

Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».

Название величины	Обозначение	Единица измерения	Формула
Объем тела	V	м³	V_т = F_A / pg
*Плотность жидкости*	p	кг/м³	p_ж = F_A / (Vg)
*Сила Архимеда*	F_A	Н	F_A = p_ж V_т g
Постоянная	g ≈ 10 Н/кг	Н/кг

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Тело объемом 2 м³ погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м³, погруженный в воду на половину своего объема.

Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7.
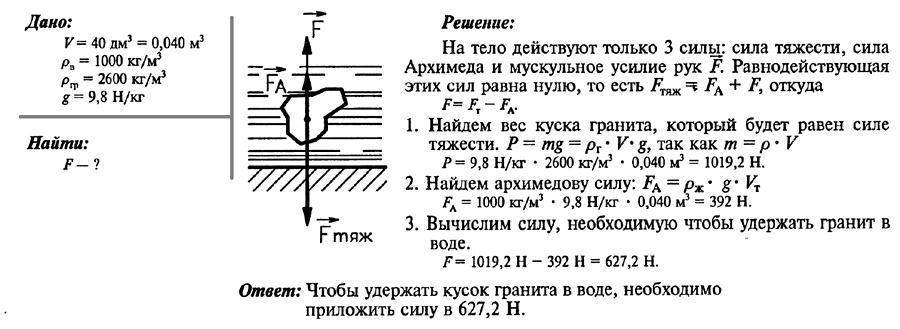
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм³?

Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.

Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м³, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м³.

Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V₁ – объем цилиндра, погруженного в масло (V₁= V – V₂ = Sh₁); h₁ – высота части цилиндра, погруженной в масло; V₂ – объем цилиндра, погруженного в воду после добавления масла; р_в – плотность воды (1000 кг/м³); р_м – плотность масла (800 кг/м³)

Найти: (h – h₁) / h — ?

Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9p_вgV
F₁ – сила, выталкивающая цилиндр из масла F₁ = p_мgV₁F₂ – сила, выталкивающая цилиндр из воды после добавления масла F₂ = p_вgV₂Баланс сил: F – F₁ = F₂0,9p_вgV – p_мgV₁ = p_вgV₂ V₁= V – V₂ ⇒ 0,9p_вV – p_м(V – V₂) = p_вV₂

V(0,9p_в – p_м) = V₂(p_в – p_м) V = Sh; V₁= Sh₁ ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).

Задача № 12.
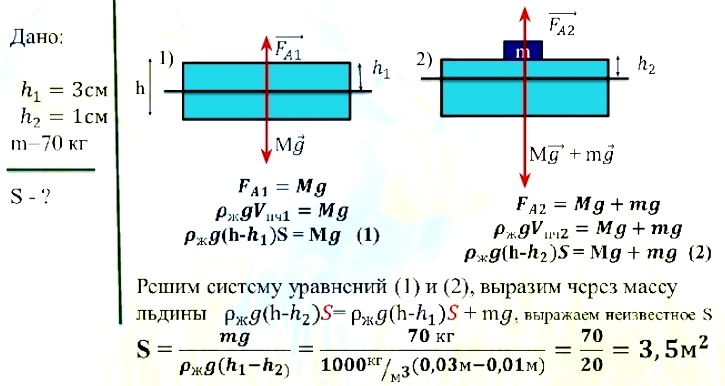
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.

Ответ: 3,5 м³.

Теория для решения задач.

Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = р_атм + p*g*h

Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».

Следующая тема: «Задачи на механическую работу».

Источник

4. Статика и механические колебания

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Гидростатика. Сила Архимеда

Закон Архимеда

На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.

Выталкивающая сила (сила Архимеда) равна

[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.

Плавание тел

Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то

[mg=rho g V,] [F_A=rho_0 g V]

Имеются три возможности дальнейшего движения тела.

Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.

Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.

Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.

Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).

Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)

Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.

Ответ: 12,5

Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)

Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]

Ответ: 15

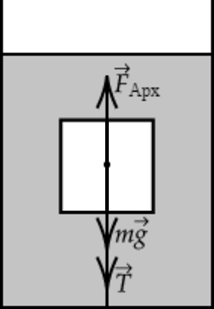
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)

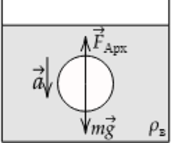
Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]

Ответ: 157

Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)

Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]

Ответ: 1

В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)

В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]

Ответ: 1,5

Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)

При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]

Ответ: 2500

Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)

Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]

Ответ: 13

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

В этой статье представляю задачи, связанные с плаванием тел и силой Архимеда. Как обычно, сначала пытаемся решить задачи простые, а затем перейдем к более сложным, которые вы найдете в следующей статье.

Задача 1. В воду погружен стеклянный кубик с ребром 10 см. Нижняя его грань находится на глубине 30 см. Рассчитайте силу давления жидкости, действующую: а) на верхнюю грань кубика; б) на нижнюю грань кубика; в) на правую грань; г) на левую грань; д) на переднюю и заднюю грани. Найдите равнодействующую всех этих сил.

Давление на грани кубика

Давление столба жидкости может быть вычислено по формуле , а сила давления может быть найдена из формулы , из которой находим: .

Не забываем, что очень важно помнить про перевод всех данных задачи в систему СИ, поэтому все расстояния и глубины из сантиметров переводим в метры.

Тогда сила давления на грань: , где — длина ребра кубика в метрах, — глубина, причем для боковых граней возьмем среднее значение () так как давление у верхнего края боковых граней и у нижнего – разное.

Сила давления на верхнюю грань, Н:

Сила давления на нижнюю грань, Н:

Сила давления на боковые грани, заднюю и переднюю, Н:

Понятно, что все силы, действующие на боковые, заднюю и переднюю грани друг друга компенсируют, а равнодействующая всех сил будет в итоге суммой сил давления на нижнюю и верхнюю грани:

Так как сила давления на нижнюю грань больше, чем на верхнюю, то равнодействующая направлена вверх.

Задача 2. Определите объем куска алюминия, на который в керосине действует архимедова сила величиной 120 Н.

Сила Архимеда может быть вычислена как , где — плотность жидкости, а — объем самого тела. То есть сила Архимеда не зависит от того, из чего сделано тело, а только от его объема. Вы спросите: почему тогда одинаковые по объему тела, например, шарики равных радиусов, сделанные из дерева и какого-либо металла, по-разному себя ведут в воде: один плавает, второй – тонет? Да просто есть ведь и сила тяжести, которая зависит как раз от массы тела, и в случае деревянного шарика сила Архимеда достаточна, чтобы компенсировать силу тяжести, а в случае с металлическим шариком – нет.

Рассчитаем объем: м

Задача 3. Плавающий деревянный брусок вытесняет 0,5 л воды. Сколько весит брусок?

Так как брусок плавает, то сила Архимеда равна силе тяжести. Нас спрашивают в задаче про вес бруска. Так как система в покое и ускорения нет, то вес бруска равен силе тяжести:

Можно эту задачу решить иначе: вес тела равен весу воды, вытесняемой им. Брусок вытеснил 0,5 литра воды. Воспользовавшись формулой плотности вещества, определяем, что масса такого количества воды равна 0,5 кг, а вес, значит, 5Н.

Задача 4. Тела изготовлены из дерева, пробки и стали. Они имеют объем 100 см каждое. Найдите архимедову силу, действующую на каждое тело, если его погрузить в воду.

Как было показано в одной из предыдущих задач, неважно, из чего изготовлено тело, а важен его объем, поэтому, раз тела обладают одним и тем же объемом, то и сила Архимеда на них действует одинаковая:

Ответ: 1 Н

Задача 5.Тело при погружении в воду становится легче в 5 раз, чем в воздухе. Определите плотность этого тела.

Мы с вами помним, конечно, что на всякое тело, погруженное как в жидкость, так и в газ, действует сила Архимеда. Поэтому в воздухе она также будет действовать на тело. Однако плотность воздуха так мала по сравнению с плотностью воды, что, я думаю, мы этой силой пренебрежем, и примем вес тела в воздухе равным силе тяжести.

Тогда вес тела — на воздухе, а вес тела в воде . А уменьшился вес этого тела в воде благодаря силе Архимеда: , откуда получаем, что

Масса тела равна произведению его плотности на объем:

Подставим:

Откуда и найдем плотность тела:

Ответ: плотность тела 1250 кг/м

Задача 6. На предмет, целиком погруженный в керосин, действует выталкивающая сила величиной 2 кН. Какой будет архимедова сила, действующая на него в воде? А в спирте?

Чтобы узнать, какой будет Архимедова сила, нужно знать объем предмета. Определим его, зная Архимедову силу в керосине: , откуда получаем, что .

Зная объем, определяем Архимедову силу в воде, Н:

Так как плотность спирта равна плотности керосина, то и Архимедовы силы в этих жидкостях будут одинаковы.

Задача 7.Цинковый шар имеет массу 360 г. При погружении в воду его вес становится равным 2,8 Н. Сплошной этот шар или полый?

Определим объем шара в предположении, что полости в нем нет, по формуле плотности (то есть найдем объем куска цинка массой 360 г):

Плотность цинка равна кг/м, объем получается м

Теперь определим реальный объем шара, то есть тот, который он вытесняет, по известному весу в жидкости. Вес шара Н, вес в жидкости равен , откуда объем вытесняемой жидкости (и объем шара)

мы получили больший объем, чем в первом случае, то есть шар имеет полость внутри, которая и влияет на его внешний объем.

Задача 8. Камень имеет объем 7,5 дм и массу 18,7 кг. Какую силу придется приложить, чтобы удерживать его в воздухе и в воде?

Чтобы удержать такой камень в воздухе, нужно преодолеть силу тяжести, то есть Н.

Теперь определим, какую силу достаточно будет приложить в воде, ведь там нам поможет сила Архимеда!

Тогда сила, которую нужно приложить в воде для удержания камня (или, проще, вес этого камня в воде) равна Н

Задача 9. Сплошное однородное тело, будучи погруженным в воду, весит 170 мН, а в глицерин – 144 мН. Каким будет вес этого тела, если его погрузить в четыреххлористый углерод?

Запишем систему уравнений по тем условиям, что описаны в задаче. Вес тела в воде равен весу тела на воздухе, уменьшенному на силу Архимеда:

Вес тела в глицерине равен весу тела на воздухе, уменьшенному на силу Архимеда – только в глицерине сила Архимеда отличается от той, что действовала на тело в воде:

Из этих двух уравнений, объединив их в систему, можно найти объем тела. Вычтем второе уравнение из первого:

Подставляем числа:

Теперь, когда мы знаем объем тела и плотность четыреххлористого углерода, можно найти силу Архимеда в нем:

Ответ: 110 мН

Задача 10. Кусок парафина толщиной 5 см плавает в воде. Он имеет форму прямоугольного параллелепипеда. Какая часть куска выступает над водой?

Если кусок парафина плавает, а не тонет, значит, сила Архимеда достаточна для того, чтобы компенсировать силу тяжести. Тогда можно записать:

Представим массу куска через его объем и плотность:

Здесь — объем всего куска, а — объем погруженной части.

Тогда:

Так как объем – это произведение площади основания на высоту, то можно сократить площадь:

Откуда делаем вывод, что , то есть из пяти см выступает 0,5 см.

Задача 11. Прямоугольная баржа после приема груза осела на 0,5 м. Принимая длину баржи 5 м, а ширину – 3 м, рассчитать вес принятого ею груза.

Рассчитаем объем воды, который был вытеснен баржей после осадки:

Такой объем воды весит 7,5 тонн – это легко понять, помня величину плотности воды.

То есть вес груза, принятого баржей, равен , или 75 кН.

Задача 12. Плот состоит из 12 бревен, каждое из которых имеет объем 0,8 м. Бревна сосновые. Можно ли на этом плоту переправить на другой берег автомобиль массой 1,5 тонны?

Рассчитаем вес плота: Н

К этому весу будет еще добавлен вес автомобиля: Н

Определим силу Архимеда. Если она окажется больше, чем суммарный вес плота и автомобиля, то плот выдержит (не будет затоплен при переправе), а если меньше, то переправлять автомобиль нельзя. Предположим, весь объем плота оказывается в воде при погрузке автомобиля. Тогда сила Архимеда: Н.

Так как , то делаем вывод, что плот может переправить автомобиль и даже не погрузится при переправе целиком в воду, то есть колеса не намокнут.

Задача 13. Теплоход, вес которого вместе с оборудованием составляет 20 МН, имеет объем подводной части при погружении до ватерлинии 6000 м. Как велика грузоподъемность теплохода?

Сразу вычислим силу Архимеда, так как знаем водоизмещение судна:

Н.

Часть этой силы пойдет на компенсацию веса самого судна с оборудованием:

, или 40 МН – такого веса груз можно нагрузить на теплоход.

Задача 14. В сообщающиеся сосуды диаметром каждый налита жидкость плотностью . В один сосуд опустили тело массой , которое стало плавать в жидкости. Как и на сколько изменится уровень жидкости в сосудах?

Тело в одном из двух сосудов

Так как тело плавает, то заключаем, что сила Архимеда достаточна, чтобы скомпенсировать вес тела. Тогда запишем это формулой:

Так как сосудов два, и по закону уровень воды в них одинаков, то, если общий объем воды увеличивается на благодаря телу, то в каждом сосуде он поднимется на .

Высота подъема воды равна

Или

Источник

Сила Архимеда

Теория

Задачи

Задачи на силу Архимеда с решениями

Название величины

Обозначение

Единица измерения

Формула

Объем тела

V

м3

Vт = FA / pg

Плотность жидкости

p

кг/м3

pж = FA / (Vg)

Сила Архимеда

FA

Н

FA = pж Vт g

Постоянная

g ≈ 10 Н/кг

Н/кг

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Теория для решения задач.

Гидростатика. Сила Архимеда

м³

V_т = F_A / pg

кг/м³

p_ж = F_A / (Vg)

F_A

F_A = p_ж V_т g