Решу егэ биология справочные материалы

Геометрия

• Треугольник
• Четырехугольники
• Окружность и круг
• Призма
• Пирамида
• Усеченная пирамида
• Цилиндр
• Конус
• Усеченный конус
• Сфера и шар

1. Формулы сокращённого умножения

Наверх

2. Модуль числа

Определение:

Основные свойства модуля:

Наверх

3. Степень с действительным показателем

Свойства степени с действительным показателем

Пусть Тогда верны следующие соотношения:

Наверх

4. Корень n-ой степени из числа

Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.

Основные свойства арифметического корня:

Наверх

5. Логарифмы

Определение логарифма:

Основное логарифмическое тождество:

Основные свойства логарифмов

Пусть Тогда верны следующие соотношения:

Наверх

6. Арифметическая прогрессия

Формула n-го члена арифметической прогрессии:

Характеристическое свойство арифметической прогрессии:

Сумма n первых членов арифметической прогрессии:

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

7. Геометрическая прогрессия

Формула n-го члена геометрической прогрессии:

Характеристическое свойство геометрической прогрессии:

Сумма n первых членов геометрической прогрессии:

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

8. Бесконечно убывающая геометрическая прогрессия

Сумма бесконечно убывающей геометрической прогрессии:

Наверх

9. Основные формулы тригонометрии

Зависимость между тригонометрическими функциями одного аргумента:

Формулы сложения:

Формулы тригонометрических функций двойного аргумента:

Формулы понижения степени:

Формулы приведения

Все формулы приведения получаются из соответствующих формул сложения. Например:

Применение формул приведения укладывается в следующую схему:

— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;

— определяется знак приводимой функции;

— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или , то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид , то функция названия не меняет.

Например, получим формулу :

— — IV четверть;

— в IV четверти тангенс отрицательный;

— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,

Формулы преобразования суммы тригонометрических функций в произведение:

Формулы преобразования произведения тригонометрических функций в сумму:

Наверх

10. Производная и интеграл

Таблица производных некоторых элементарных функций

Правила дифференцирования:

1.

2.

3.

4.

5.

Уравнение касательной к графику функции в его точке :

Таблица первообразных для некоторых элементарных функций

Правила нахождения первообразных

Пусть ― первообразные для функций и соответственно, a, b, k ― постоянные, Тогда:

— ― первообразная для функции

— ― первообразная для функции

— ― первообразная для функции

— Формула Ньютона-Лейбница:

1. Треугольник

Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно; ― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно; ― длины высот AA₂, BB₂, CC₂ треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC; ― площадь треугольника ABC. Тогда имеют место следующие соотношения:

(теорема синусов);

(теорема косинусов);

Наверх
2. Четырёхугольники

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, все стороны которого равны.

Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырехугольника

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Наверх

3. Окружность и круг

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга,  — длина дуги в градусов,  — длина дуги в радиан,  — площадь сектора, ограниченного дугой в n градусов,  — площадь сектора, ограниченного дугой в радиан. Тогда имеют место следующие соотношения:

Вписанный угол

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Вписанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Описанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны

Наверх

4. Призма

Пусть H ― высота призмы, AA₁ ― боковое ребро призмы,  ― периметр основания призмы,  ― площадь основания призмы,  ― площадь боковой поверхности призмы,  ― площадь полной поверхности призмы, V ― объем призмы,  ― периметр перпендикулярного сечения призмы,  ― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

Свойства параллелепипеда:

— противоположные грани параллелепипеда равны и параллельны;

— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;

— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Наверх

5. Пирамида

Пусть H ― высота пирамиды,  ― периметр основания пирамиды,  ― площадь основания пирамиды,  ― площадь боковой поверхности пирамиды,  ― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:

;

.

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то

Наверх

6. Усечённая пирамида

Пусть H ― высота усеченной пирамиды, и  ― периметры оснований усеченной пирамиды, и  ― площади оснований усеченной пирамиды,  ― площадь боковой поверхности усеченной пирамиды,  ― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.

Тогда имеют место следующие соотношения:

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то:

Наверх

7. Цилиндр

Пусть h ― высота цилиндра, r ― радиус цилиндра,  ― площадь боковой поверхности цилиндра,  ― площадь полной поверхности цилиндра, V ― объем цилиндра.

Тогда имеют место следующие соотношения:

Наверх

8. Конус

Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса,  ― площадь боковой поверхности конуса,  ― площадь полной поверхности конуса, V ― объем конуса.

Тогда имеют место следующие соотношения:

Наверх

9. Усечённый конус

Пусть h ― высота усеченного конуса, r и  ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,  ― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:

Наверх

10. Сфера и шар

Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы,  ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,  ― объем сегмента, высота которого равна h,  ― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:

Наверх

Распределение тематик заданий

«Биология как наука. Методы научного познания»

В данном блоке проверяется знание материала о достижениях биологии, методах исследования, об основных уровнях организации живой природы.

«Клетка как биологическая система»

В данный раздел входят задания, проверяющие: знания о строении, жизнедеятельности и многообразии клеток; умения устанавливать взаимосвязь строения и функций органоидов клетки, распознавать и сравнивать клетки разных организмов, процессы, протекающие в них.

«Организм как биологическая система»

В данном разделе проверяется усвоение знаний о закономерностях наследственности и изменчивости, об онтогенезе и воспроизведении организмов, о селекции организмов и биотехнологии, а также выявляется уровень овладения умениями применять биологические знания при решении задач по генетике.

«Система и многообразие органического мира»

Проверяются: знания о многообразии, строении, жизнедеятельности и размножении организмов различных царств живой природы и вирусах; умения сравнивать организмы, характеризовать и определять их принадлежность к определённому систематическому таксону.

«Организм человека и его здоровье»

Данный блок направлен на определение уровня освоения системы знаний о строении и жизнедеятельности организма человека.

«Эволюция живой природы»

Сюда включены задания, направленные на контроль: знаний о виде, движущих силах, направлениях и результатах эволюции органического мира; умений объяснять основные ароморфозы в эволюции растительного и животного мира, устанавливать взаимосвязь движущих сил и результатов эволюции.

«Экосистемы и присущие им закономерности»

Этот блок содержит задания, направленные на проверку: знаний об экологических закономерностях, о круговороте веществ в биосфере; умений устанавливать взаимосвязи организмов в экосистемах, выявлять причины устойчивости, саморазвития и смены экосистем.

Распределение заданий экзаменационной работы по содержательным разделам курса биологии

Разделы	Количество заданий
Первая часть	Вторая часть	Вся работа
Биология как наука.	1	1	2
Клетка как биологическая система.	4-3	1	5-4
Организм как биологическая система.	3-4	1	4-5
Система и многообразие органического мира.	3	1	4
Организм человека и его здоровье.	4	1	5
Эволюция живой природы.	3	1	4
Экосистемы и их закономерности.	3	1	4
Итого	21	7	28

В 2023 году школьники сдают ЕГЭ по биологии, который относится к экзаменам по выбору. Он потребуется тем, кто желает поступить в вуз и получить специальность, связанную с медициной, физкультурой, спортом, естественными науками.

Подготовка

Невозможно получить высокую оценку без уверенных знаний и регулярного
повторения. ЕГЭ по биологии сложен тем, что включает в себя большой объём информации, который не каждый может запомнить. На государственном испытании будут затронуты все без исключения темы, которые экзаменуемые проходили в классе. Чтобы балл порадовал, необходимо все уложить в голове «по полочкам».

Как правильно готовиться:

• в первую очередь рекомендуется ознакомиться с электронными
  версиями контрольно-измерительных материалов, просмотреть вопросы и понять их структуру;
• среди просмотренных тем нужно выделить те, с которыми придется «повозиться»;
• после этого можно переходить к теоретической части, обращаясь к школьной
  программе;
• дополнительно к учебникам логично использовать специальные пособия и дополнительные материалы;
• закрепите пройденное, прорешайте задания онлайн, чтобы стимулировать запоминание и добиться автоматизации, а также снизить стресс, который возникнет, когда придет «время Икс».

Вся теория в виде подборок по теме есть в сети Интернет. Услуга
репетитора может понадобиться, если самостоятельно не получается добиться
эффекта.

Есть нюансы

На госэкзамене школьники столкнутся с вопросами, которые отражают
все темы, изучаемые ранее. Стоит уделить внимание таким понятиям как:

• Что такое клетка и каково ее строение;
• Группы крови, сердце
  (его строение и работа);
• Что такое анализаторы и каково их строение;
• Животные — ткани,
  органы, виды и их особенности;
• Организм – спинной мозг, нервная, эндокринная, выделительная системы;
• Грибы и растения – классификации, строение и особенности;
• Растения – ткани, вегетативные и генеративные органы, плод, циклы развития, двойное оплодотворение, мир растений и его систематизация;
• Системы обмена веществ и дыхания;
• Биологические процессы – иметь представление о митозе, мейозе, метаболизме, фотосинтезе, онтогенезе.
• Генетика;

Совет

• Изучая биологию, обязательно делайте конспекты, фиксируя
  проблемные моменты;

• разбирайтесь в тех темах, которые вызывают сложности;

• работайте с таблицами, рисунками, схемами, чтобы лучше запоминать;

• если не знаете ответа, отмечайте тот, который кажется наиболее подходящим. Все вопросы следует прорешать.

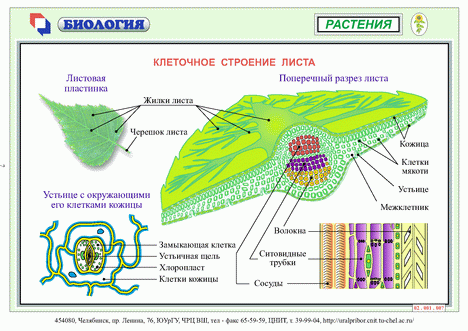
«Ткани растения»

Ткань — группа клеток, сходных по строению и выполняющих одинаковые функции.

Ткань	Где располагается	Особенности строения клеток	Значение
Образовательная (меристема)	Верхушки стеблей Кончики корней Камбий (между лубом и древесиной) Рана	Мелкие делящиеся клетки без вакуолей	Рост растения
Покровная	Эпидермис (кожица) Покрывает листья и молодые побеги	1 ряд плотно прилегающих живых клеток, без хлоропластов. Имеются устьица для газообмена	Уменьшение испарения, газообмен
Пробка	Несколько рядов плотно прилегающих мёртвых клеток, заполненных воздухом. Для газообмена -чечевички	Защита от потери влаги, колебаний температуры, бактерий
Кора	Многослойная мёртвая ткань	Защита от температурных колебаний,.. вредителей
Механическая	В лубе, древесине	Толстые одревесневшие оболочки	Опора органам растения
Проводящая	Луб (флоэма)	Образован ситовидными трубками. Они представляют собой ряды тонких длинных живых клеток без ядер. Поперечные стенки между ними пронизаны отверстиями, как сито	Транспорт воды и органических веществ из листьев к корням
Древесина (ксилема)	Состоит из сосудов. Сосуды образованы мёртвыми вытянутыми клетками с утолщёнными оболочками, горизонтальные перегородки между ннми разрушены	Транспорт воды и минеральных веществ из корня к листьям
Основная (паренхима)	Мякоть листа Сердцевина стебля Корень	Хлоропласты в клетках	Образование и накопление питательных веществ
Выделительная	Нектарники Железы		Выделение эфирных масел, воды, нектара

. Органы растений. Вегетативные обеспечивают основные процессы  жизнедеятельности Генеративные – обеспечивают размножение растений 1. Побег 1.Цветок 2. Корень 2. Семя 3. Плод
Вегетативные органы: Побег – стебель с расположенными на нем листьями и почками. Стебель Ось побега растения. Опора растения, проводит питательные вещества, осуществляет связь между корнями и листьями Листья Часть побега.  Необходим для дыхания, образования питательных веществ, испарения воды. Почки Зачаточный побег (листовой и цветочный)
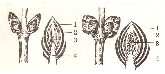
Рассмотрите строение двух видов почек растения. Определите, какая из них является листовой (вегетативной), а какая цветочной (генеративной). Рис. 2 “Сравнение строения вегетативной и генеративной почек.  Части почки Вегетативная почка Генеративная почка Зачаточный стебель Зачаточные листья Зачаточные почки Зачаточные соцветия Почечные чешуи
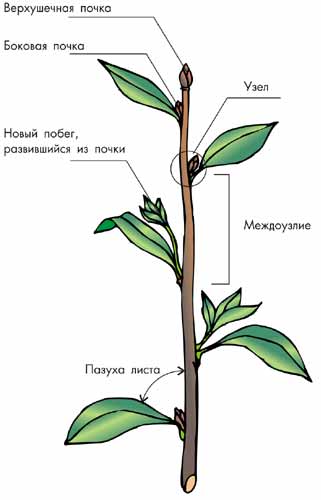
Стебель – ось побега, он связывает корни и листья Строение стебля. Стебель – вегетативный орган растения, на котором укрепляются листья, цветки, плоды. Стебель осуществляет передвижение воды и минеральных солей от корня к листьям и органических веществ, образованных в листьях, вниз к корням. В зеленых стеблях происходит фотосинтез. У многих растений в стебле накапливается запасные питательные вещества. Стебель может служить и органом вегетативного размножения. По направлению и способу роста различают стебли прямостоячие, ползучие, стелющиеся, лазающие, цепляющиеся. У некоторых растений стебель укорочен и листья образуют прикорневую розетку. Стебли растений характеризуются большим разнообразием по форме поперечного сечения, размерам, характеру и направлению роста. Побег состоит из повторяющихся элементов – узлов и междоузлий. Участки стебля на котором развиваются листья, называются узлами, а части стебля между соседними узлами – междоузлиями.
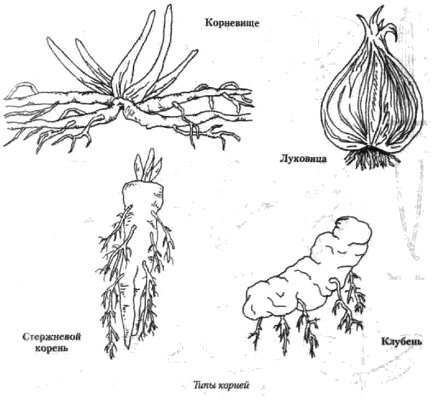
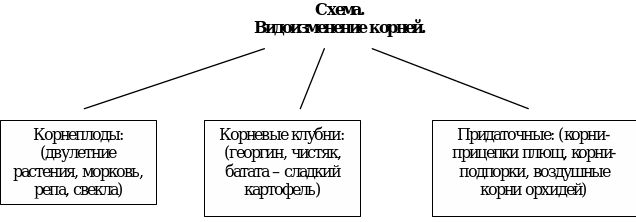
Видоизменения побега
Ли́ст—наружный орган растения, основной функцией которого является фотосинтез. Для этой цели лист, как правило, имеет пластинчатую структуру, чтобы дать клеткам, содержащим специализированный пигмент хлорофилл в хлоропластах, получить доступ к солнечному свету. Лист также является органом дыхания, испарения и гуттации (выделения капель воды) растения. Листья могут задерживать в себе воду и питательные вещества, а у некоторых растений выполняют и другие функции.
Эпиде́рмис — слой клеток, которые защищают от вредного воздействия среды и излишнего испарения воды. Часто поверх эпидермиса лист покрыт защитным слоем восковидного происхождения (кутикулой). Мезофи́лл, или паренхи́ма — внутренняя хлорофиллоносная ткань, выполняющая основную функцию — фотосинтез. Сеть жи́лок, образованных проводящими пучками, состоящими из сосудов и ситовидных трубок, для перемещения воды, растворённых солей, сахаров и механических элементов. У́стьица — специальные комплексы клеток, расположенные, в основном, на нижней поверхности листьев; через них происходит испарение воды и газообмен Какое значение в жизни растения имеет листопад? 1) К осени в клетках листьев накапливаются ненужные растениям, а иногда и вредные для них вещества. Начинается листопад. Вместе c опадающими листья из растений удаляются и эти вещества. 2) Зимой корни многих растений не могут всасывать из почвы холодную воду. Если бы наши деревья и кустарники не сбрасывали листья, они погибли бы от недостатка влаги. Но у некоторых цветковых растений листья сохраняются всю зиму. Это вечнозеленые кустарнички брусника, вереск, клюква. Мелкие плотные листья этих растений, слабо испаряющие воду, сохраняются под снегом. Листопад – это приспособление растений к уменьшению испарения осенью и зимой
Функции видоизмененных листьев Примеры Усики Закрепление лазающего стебля Горох, вика, чина Чешуи тонкие Защитная функция Репчатый лук Чешуи сочные Запасание питательных веществ Репчатый лук Колючки Уменьшение испарение влаги, защита от поедания животными Кактус, верблюжья колючка, барбарис Ловчие аппараты насекомоядных Улавливание и переваривание насекомых Росянка, непентес, венерина мухоловка
Корень – осевой орган, анатомически сходный со стеблем. Выполняет функции: Укрепление растения в почве Всасывание воды и минеральных веществ из почвы Запасание органических веществ Вегетативное размножение
Корневая система- совокупность всех корней растения Боковые корни (отходят от главного) Главный корень Придаточные (отрастают от стебля и др. частей растения)
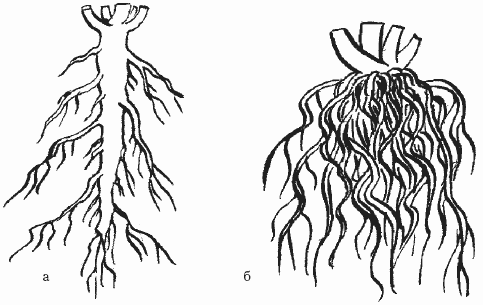
Стержневая и мочковатая корневая системы
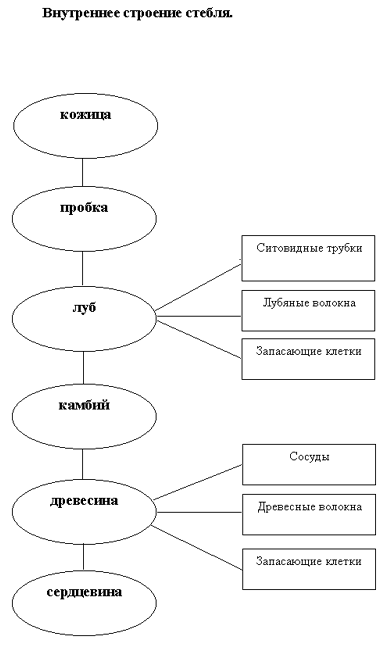
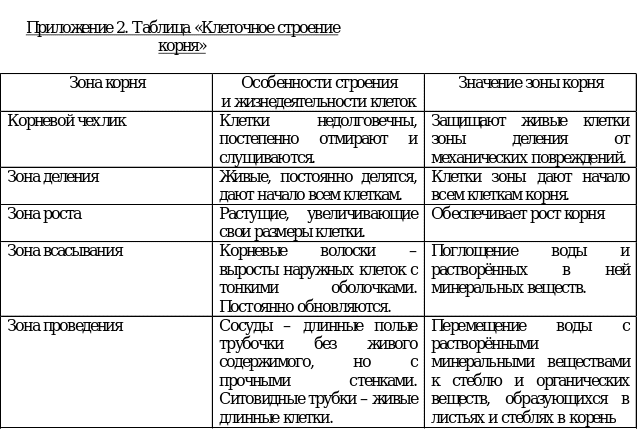
Строение корня Анатомия корня такая же, как и у стебля (те же слои и в том же порядке) В связи с главной функцией корня (всасыванием) в нём сформировались зоны

2. Генеративные органы:

Цветок – видоизмененный побег, на месте которого созревает плод с семенами или одним семенем.

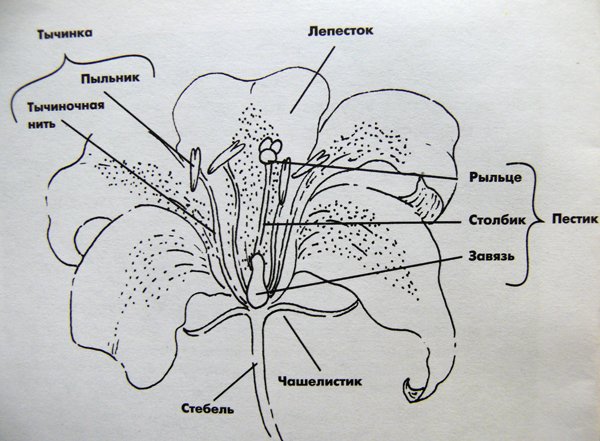
Тычинка – мужская часть цветка. Она состоит из тычиночной нити и пыльника, в котором развивается пыльца. Внутри пыльников развивается пыльца, а тычиночная нить поднимает его на нужную высоту. Число тычинок в разных цветках различно. Внутри пыльника созревают пыльцевые зерна. По размеру – это одна клетка. Снаружи пыльцевые зерна покрыты плотной оболочкой, имеют шипики, зубчики, бугорки и бороздки. По форме пылинки можно определить растение, которому она принадлежит. У насекомоопыляемых цветков пыльца крупная и клейкая, у ветроопыляемых – мелкая и сухая.

Пестик – женская часть цветка, расположен в центральной его части. Верхняя часть пестика – рыльце, его роль – удержание пыльцы. Средняя часть – столбик и нижняя – завязь, где расположены одна или несколько семяпочек.

Для того чтобы удержать пыльцу, рыльце может быть шероховатым или на нем выделяется клейкая жидкость. А у ветроопыляемых растений оно напоминает ершик для мытья посуды. Столбик служит для поднятия пестика на определенную высоту. А из завязи образуется плод.

— Большинство цветков имеют и пестик и тычинки. Но есть цветки, которые имеют или тычинки или пестики.

Цветок, имеющий пестик и тычинки называется обоеполым.

Если цветок имеет либо пестик, либо тычинки, он называется однополым. Если в цветке только пестик – это женский цветок, если только тычинки – это мужской цветок.

Цветки и насекомые.

О многом может рассказать цветок. Но в первую очередь он расскажет, как опыляется: с помощью ветра или насекомых (Приложение 2) и даже какими насекомыми.

Конечно, пчелы и бабочки, мухи и прочие насекомые посещают цветки не ради того, чтобы способствовать их опылению. У насекомых здесь свои корыстные интересы. Какие же именно?

Прежде всего, насекомых привлекает к цветку пыльца – питательный, высококалорийный продукт, в изобилии содержащий белки, углеводы, жиры и витамины и в какой то мере сравнимый с черной и красной икрой. Пчелы собирают ее для потомства. Мухи, жуки и масса других насекомых сами лакомятся пыльцой. Отсюда понятно, почему во многих цветках пыльцы образуется гораздо больше, чем используется для опыления.

Но и это не главная цель посещения цветов насекомыми.

Притягательно для насекомых наличие в цветке нектара – богатой сахарами жидкости. Нектарники могут располагаться в самых разных частях цветка. Это связано с тем или иным способом опыления и соответствующей ему конструкцией цветка. Обычно нектарники расположены так, что при каждой попытке добыть сладкий сок насекомые должны платить растению своеобразную дань: уносить или приносить на своем тельце пыльцу и производить опыление.

Но насекомым нужен сигнал о наличии его: ярко – окрашенный или с достаточно сильным запахом цветок.

Поскольку цветки, как правило, располагаются на общем зеленом фоне, окраска их резко контрастирует с зеленым цветом. В центральных и северных областях нашей страны чаще всего можно найти белые и желтые, чуть реже красные, еще реже синие и фиолетовые. Окраска цветка не случайна. Дело в том, что каждый вид насекомых предпочитает определенный цвет. И окраской цветок привлекает именно «своих» насекомых, которые только и смогут произвести опыление. Для пчел – синий и фиолетовый, чисто пурпурный, бабочек кроваво – красные, а в тропиках колибри. Ночные бабочки особенно охотно посещают белые и бледно — желтые цветки. Это понятно, в темноте ночи наиболее различим именно белый цвет.

Чашелистики тоже могут приобретать ту или иную окраску (прострел, горицвет, борец). Даже верхние листья побега (марьянник). Это необходимо для увеличения окрашенной площади, для того, чтобы быть более заметным издалека. Туже цель преследует и объединение отдельных цветков в соцветия.

Строение цветка отражают специальными формулами, для которых используют общепринятые в ботанике сокращения

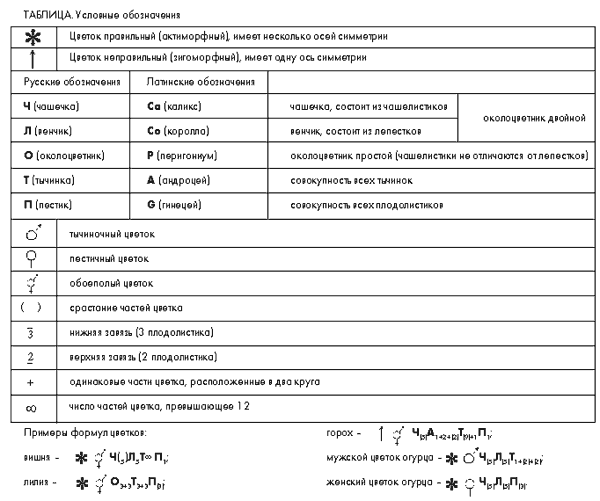
Семя

Семена развиваются из семязачатков, находящихся у цветковых растений в завязях пестиков.

Строение семени

Семя имеет

• семенную кожуру, образующуюся из покровов семязачатка.

• Зародыш (представляет собой зачаточное растение, находящееся на той или иной стадии развития. Обычно в зародыше различимы семядоли (1 или 2), зачаточный стебель с конусом нарастания,. зачаточный корень (при прорастании семени он превратится в главный корень)

• эндосперм (представляет собой ткань, в которой отлагается запас питательных веществ для прорастания семени. В созревших плодах некоторых растений эндосперма нет, потому что он поглощается ещё на ранних стадиях развития зародыша или запасается в семядолях, т. е. первых листьях зародыша (как у бобовых)

Строение семян злаков (например, пшеницы) своеобразно. Семенная кожура срастается с околоплодником. Эндосперм прилегает к так называемому щитку — той части зародыша, которая является единственной семядолей. При прорастании семени питательные вещества поступают в растущие органы через щиток.

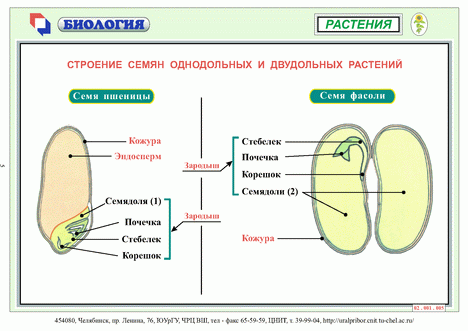
Плод – орган защиты и распространения семян, конечный этап развития цветка. Содержит семена, окружённые околоплодником. Околоплодник образуется при разрастании стенок завязи.

	Тип плода	Вид плода	Название растения
сочные	Односемянный	Костянка	Вишня, слива, черешня
Многосемянный	Ягода	Томат, крыжовник
Яблоко	Яблоня, груша
сухие	Односемянный	Семянка	Подсолнечник
Зерновка	Пшеница, рожь
Многосемянный	Коробочка	Мак
Боб	Горох, боб
Стручок	Капуста, акация

Размножение растений

Цветковые растения размножаются вегетативным или половым путём. Вегетативное размножение происходит при помощи вегетативных органов (листовые черенки, стеблевые черенки, корневые черенки, корневые отпрыски,, усы, отводки, прививка, корневища, клубни, луковицы). Половое размножение связано с гаметами. У растений наблюдается регулярная смена ядерных фаз: гаплоидной и диплоидной. В жизненном цикле высших растений чередуются два поколения: гаметофит и спорофит. Гаметофит образует гаметы. У семенных растений гаметофиты утратили способность к самостоятельному существованию. Преобладающим поколением стал спорофит. Он образуется после слияния гамет. Цветок можно считать гаметофитом и спорофитом, так как он образует вначале споры — мужские и женские — а затем из низ развиваются гаметы. У цветковых растений оплодотворению предшествует опыление.

Виды опыления:

• самоопыление (у обоеполых цветков)

• перекрёстное (с помощью ветра или насекомых) У ветроопыляемых растений цветки мелкие, собраны в соцветия, цветут до распускания листьев, пыльца мелкая и сухая, тычинки с длинными тычиночными нитями, рыльца пестиков перистые и далеко выдаются из цветков. Растут группами. У насекомоопыляемых растений цветки крупные, яркие, вырабатывают нектар, обладают запахом, пыльца крупная, липкая

У цветковых растение в оплодотворении участвует одновременно 2 спермия (двойное оплодотворение). Один спермий сливается с яйцеклеткой (формирование зародыша – диплоидный набор хромосом), второй спермий сливается с диплоидным центральным ядром ( в результате образуется эндосперм с триплоидным набором хромосом). Эндосперм – это запас питательных веществ для молодого растения

«Систематика цветковых растений»

Систематика – наука о классификации организмов, родственных друг с другом.

Классификация – объединение организмов в группы по степени их родства.

Признаки класса	Класс Двудольные	Класс Однодольные
Число семядолей в зародыше семени	2 семядоли	1 семядоля
Тип корневой системы	Стержневая	Мочковатая
Характер жилкования	Сетчатое	Дуговое или параллельное

Задания по ботанике в ходе ЕГЭ 2002-2008 годов. Царство Бактерии.

1. С какой целью прореживают всходы моркови?

2. Перечислите основные признаки цветковых растений, по которым их выделяют в отдельную систематическую группу.

3. Перечислите способы увеличения урожайности картофеля.

4. Объясните, почему необходимо окучивать картошку.

5. Какой процесс в жизни дерева нарушается пари удалении его коры?

6. Какая ткань цветковых растений связывает все органы в единое целое?

7. С какой целью проводят побелку стволов и крупных ветвей плодовых деревьев?

8. Какие признаки характерны для хвойных растений?

9.  Почему грибы выделяют в особое царство органического мира? 2002,2004, 2008

10.  Каковы особенности строения и жизнедеятельности мхов? 2002,2008

11.  Какие признаки характерны для покрытосеменных растений?

12.  Какие признаки характерны для царства растений?

13. Цветки многих покрытосеменных растений опыляются насекомыми. Объясните, в чем проявляется взаимная польза перекрестного опыления для насекомых и растений?

14. Какова роль мхов в природе?

15. С какой целью при пересадке рассады капусты прищипывают кончик корня?

Начиная с 2006 года

1. Садоводы при пикировке рассады капусты прищипывают верхушку главного корня, а при размножении кустов смородины используют стеблевые черенки, на которых развиваются придаточные корни. Оба этих растения относят к классу двудольные, Объясните, какой тип корневой системы будет у капусты, выросшей их этой рассады, а какой у смородины, выросшей из стеблевого черенка.

2. Объясните, какие основные причины «цветения воды» в водоемах.

3. Какие особенности строения и жизнедеятельности покрытосеменных способствовали их процветанию на Земле?

 2007 год

1. Почему вспашка почвы улучшает условия жизни культурных растений?

2. В листьях растений интенсивно протекает процесс фотосинтезе. Происходит ли он в зрелых и незрелых плодах? Ответ поясните.

3. Докажите, что корневище растения – видоизмененный побег.

4. Какие процессы обеспечивают передвижение воды и минеральных веществ по растению. Ответ поясните.

5. Установите, какая часть луковицы лука обозначена на рисунке буквой Б, объясните ее строение и выполняемые функции.

1. Известно, что при регулярном окучивании растений (картофеля, томатов, капусты, земляники) растения лучше растут. Объясните, каким образом окучивание влияет на рост растений и почему это воздействие благоприятно.

2. Если мышь поместить под стеклянный колпак, закрытый герметично, то она вскоре погибнет. Если вместе с мышью поместить зеленое растение и оставить колпак на свету, то мышь останется жива длительное время. Объясните в чем причина этих явлений.

3. Грибникам хорошо известно, что подосиновики часто растут под осинами, а подберезовики – под березами, маслята — под соснами и лиственницами. Как называется это явление и в чем его биологический смысл?

4. Найдите ошибки в приведенном тексте. Укажите номера предложений, в которых сделаны ошибки, объясните их.

• Цветок — орган размножения покрытосеменных растений.

• Цветок представляет собой видоизмененный лист.

• Функции цветка – это половое и бесполое размножение.

• Цветок соединен со стеблем цветоножкой.

• В цветке имеются пестики и тычинки.

При хранении масса клубней картофеля сокращается, а если клубни подморожены, то они становятся сладкими. В чем причина этих явлений?

Каковы основные отличительные особенности высших растений по сравнению с низшими?

Ученые установили, что хвойные деревья (ель, сосна) менее устойчивы к загрязнению воздуха промышленными газами, чем лиственные деревья. Объясните, в чем причина этого явления.

2008 год

1. Почему грибы выделяют в особое царство органического мира?

2. Каковы особенности строения и жизнедеятельности грибов?

3. Каковы характерные признаки царства Грибов?

4. Объясните, по каким тканям и как осуществляется транспорт веществ у покрытосеменных растений?

5. Почему вспашка улучшает почвы условия жизни культурных растений?

6. Докажите, что корневище растения – видоизмененный побег.

7. Какие процессы обеспечивают передвижение воды и минеральных веществ по растению. Ответ поясните.

8. Назовите не менее 3-х особенностей наземных растений, которые позволили им первыми освоить сушу. Ответ обоснуйте.

9. Каким способом происходит спорообразование у кукушкина льна.

10. Чем отличаются покрытосеменные растения от растений остальных отделов?

11. В чем проявляется разнообразие и приспособленность покрытосеменных к образу жизни?

12. Почему покрытосеменные растения нуждаются в особенной охране?

13. Назовите приспособления растений, которые одновременно служили бы адаптациям к противоположным условиям среды (холод-жара, засуха – влага и т.д.

14. Почему для посева отбирают крупные семена?

15. Что объединяет и в чем отличие биологических объектов, изображенных на рисунке?

 

1. Какие удобрения и почему необходимо внести в почву, чтобы получить большой кочан капусты?

2. Какие удобрения и почему необходимо внести в почву, чтобы получить крупные плоды у томата?

3. Какие удобрения и почему необходимо внести в почву, чтобы получить крупные клубни картофеля?

4. Посевы каких растений применяют в сельском хозяйстве для обогащения почвы азотом?

5. Могут ли на грядке семена взойти корешками вверх, а побегами вниз, если они были посеяны как попало?

6. Чем отличаются зародыши двудольных и однодольных растений?

7. Как человек использует бактерии?

8. Какие клеточные структуры отличают растительную клетку от животной?  

Сдай ЕГЭ! Бесплатные материалы для
подготовки каждую неделю!

null

Нажимая на кнопку, вы даете согласие на обработку своих персональных
данных согласно 152-ФЗ. Подробнее

Материалы для подготовки к ЕГЭ по Биологии

Авторы статей — профессиональные репетиторы Д. А. Соловков, Т.М. Кулакова, М.А. Филатов, Л.В. Окольнова.

Видеокурсы по биологии

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.