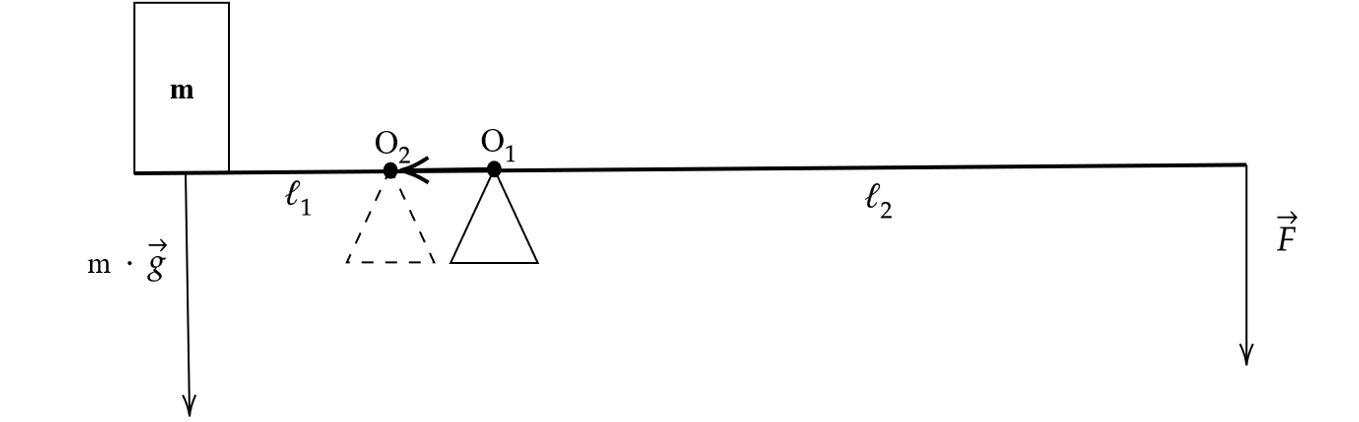Решу егэ блоки физика - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 105 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

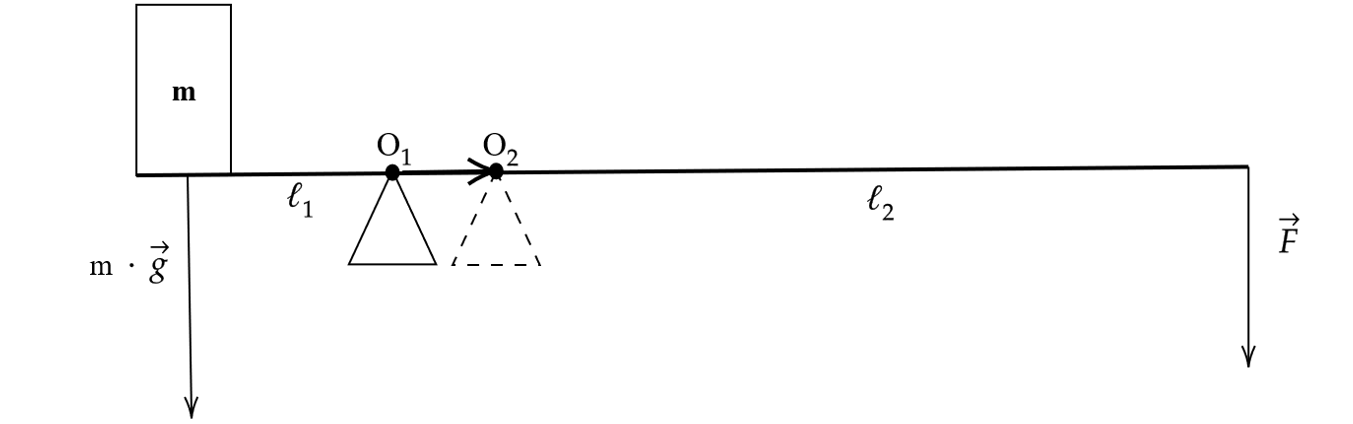
На гладкой горизонтальной плоскости лежат два груза массами и соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.

Какие законы Вы используете для описания движения брусков? Обоснуйте их применение.

На гладкой горизонтальной плоскости лежат два груза массами и соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена некоторая направленная вертикально вниз сила, в результате чего ось О движется с ускорением Найдите модуль F этой силы. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.

Какие законы Вы используете для описания движения брусков? Обоснуйте их применение.

Задания Д29 C2 № 4107

Найдите модуль ускорения A груза массой М в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза m, ускорение свободного падения равно g.

Какие законы Вы использовали для описания движения тел и блоков? Обоснуйте их применимость к данному случаю.

С помощью системы невесомых блоков на невесомых и нерастяжимых нитях уравновешены два груза (см. рис.). Модуль силы натяжения участка нити AB равен T. Установите соответствие между модулями сил натяжения и участками нитей.

На рисунке показана система, состоящая из трёх лёгких блоков и невесомого троса, с помощью которой можно удерживать в равновесии или поднимать груз массой M. Подвес груза и конец троса прикреплены к оси нижнего блока. Трение пренебрежимо мало.

На основании анализа приведённого рисунка выберите все верные утверждения и укажите в ответе их номера.

1)  Для того чтобы удерживать груз в равновесии, нужно действовать на конец верёвки с силой

2)  Изображённая на рисунке система блоков не даёт выигрыша в силе.

3)  Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок верёвки длиной 3h.

4)  Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок верёвки длиной 2h.

5)  Для того чтобы удерживать груз в равновесии, нужно действовать на конец верёвки с силой

На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода? (Ответ дайте в ньютонах.) Трение в осях блоков мало. Блоки и нити считайте невесомыми.

Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.

Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая нерастяжимая нить, на которой висит груз массой m  =  1 кг. Диски скреплены друг с другом, образуя единое целое, где R  =  10 см, r  =  5 см.

Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.

Источник: Демонстрационная версия ЕГЭ—2023 по физике

В системе, изображённой на рисунке, трения нет, блоки невесомы, нити невесомы и нерастяжимы, их участки, не лежащие на блоках, вертикальны, массы грузов равны m₁ = 1 кг, m₂  =  3 кг, m₃ = 0,5 кг. Точки подвеса груза m₂  — однородной горизонтальной балки  — находятся на равных расстояниях от её концов. Найдите модуль и направление ускорения груза массой m₃.

Какие законы Вы используете для описания движения системы грузов и блоков? Обоснуйте их применение к данному случаю.

Задания Д29 C2 № 7805

Задания Д29 C2 № 7837

Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.

На рисунке показана система, состоящая из лёгких тросов и четырёх идеальных блоков, с помощью которой можно удерживать в равновесии или поднимать груз массой M. Трение пренебрежимо мало.

На основании анализа приведённого рисунка выберите все верные утверждения и укажите в ответе их номера.

1)  Для того чтобы удерживать груз в равновесии, нужно действовать на конец верёвки с силой

2)  Для того чтобы удерживать груз в равновесии, нужно действовать на конец верёвки с силой

3)  Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок верёвки длиной 2h.

4)  Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок верёвки длиной 4h.

5)  Изображённая на рисунке система блоков не даёт выигрыша в силе.

Тонкая прямая однородная палочка длиной l установлена на ребре неподвижной призмы, вокруг которого она может свободно вращаться в вертикальной плоскости (см. рисунок). Точка опоры палочки находится ближе к её левому концу, на расстоянии от её середины. К левому концу палочки на лёгких нитях подвешен за ось невесомый блок, который может вращаться вокруг неё без трения. Через блок перекинута лёгкая нерастяжимая нить, на концах которой закреплены грузы массами и К правому концу палочки на лёгкой нити подвешен груз массой

Сделайте рисунок с указанием сил, действующих на палочку и на все грузы. Чему равна масса m палочки, если она находится в равновесии в горизонтальном положении при движении грузов m₁ и m₂ и вращении блока? Обоснуйте применимость используемых законов к решению задачи.

Задания Д4 B4 № 4082

Чтобы уравновесить на лёгкой рейке с помощью двух невесомых блоков одинаковые грузы массой М каждый, к нити, перекинутой через левый блок, и к оси правого блока необходимо приложить вертикальные силы F₁ и F₂ (см. рис.). Расстояния между чёрными точками на рейке одинаковы, трение отсутствует, нити нерастяжимы.

Можно утверждать, что

На рисунке изображена механическая система, состоящая из двух идеальных блоков, двух невесомых и нерастяжимых нитей и трёх грузов массами подвешенных на концах нитей. Определите, чему равна сила натяжения T₁ нити, к которой подвешен груз m₁.

Какие законы Вы использовали для описания движения тел и блоков? Обоснуйте их применимость к данному случаю.

Задания Д28 C1 № 3558

Какую силу давления оказывает нить на ось блока? Массы грузов одинаковы и равны Трение не учитывать. Нить невесома и нерастяжима.

1)  mg

2)   2mg

4)   4,8 mg

На рисунке изображён подъёмный механизм, с помощью которого равномерно поднимают груз массой m = 6 кг, прикладывая к концу лёгкой нерастяжимой нити некоторую силу vecF. Механизм состоит из блока 1, имеющего массу M = 2 кг, и невесомого блока 2. Трение в осях блоков пренебрежимо мало. Установите соответствие между физическими величинами и их значениями. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А)  КПД механизма,%

Б)  модуль силы натяжения нити, лежащей между блоками

Всего: 105 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.

К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рис.).

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии? (Ответ дайте в килограммах.)

На рычаг действуют две силы. Момент первой силы относительно оси вращения рычага равен 50 Н · м. Какова величина второй силы, если её плечо относительно этой же оси равно 0,5 м и рычаг при этом находится в равновесии?

Ответ дайте в Ньютонах.

Источник: Демонстрационная версия ЕГЭ—2022 по физике

Под действием веса груза mg и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).

Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)

Пройти тестирование по этим заданиям

Источник

Задачи блока С пробного ЕГЭ по физике марта 2017 года

Рассмотрим в этой статье задачи досрочного ЕГЭ по физике, прошедшего 21 марта 2017 года. Это задачи 28, 29, 30 и 31.

Задача 1.

В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, кг, кг, кг. Найдите модуль и направление ускорения груза массой .

К задаче 1

Все грузы связаны одной нерастяжимой нитью, . Следовательно, если какой-то отрезок нити будет удлиняться, то другой – укорачиваться. Запишем уравнения по второму закону Ньютона для всех грузов:

К задаче 1. Координаты

Если обозначить координаты центра блока, подвешенного к потолку, как и , а координаты тел — , — (обозначим так координату центра блока), — , то максимальный путь, пройденный телом , может быть равен

Телом 3:

Телом 2:

Сумма длин максимальных отрезков, пройденных телами, не может превышать длину нити:

То есть

Или

Теперь вернемся к нашим уравнениям по второму закону и подставим в (1) ускорения:

Тогда

Откуда

Ответ: м/c.

Задача 2.

С некоторым количеством идеального газа проводят процесс 1–2, для которого график зависимости давления от объёма представляет собой на pV-диаграмме прямую линию (см. рисунок). Параметры начального и конечного состояний процесса: атм, л, атм, л. Какой объём соответствует максимальной температуре газа в данном процессе?

К задаче 2

Уравнение такой прямой может быть записано так:

Подставим координаты точек 1 и 2 в это уравнение:

Откуда можем «вытащить» коэффициент :

Тогда можно определить :

Точке с произвольной координатой соответствует тогда давление

Или

Таким образом, произведение давления на объем (это произведение равно ) будет равно

Уже по уравнению видно, что это парабола. Определим максимум температуры. Для этого нужно определить максимальное значение произведения . Можно взять производную и приравнять к нулю:

Откуда

Ответ: 2,75 л.

Задача 3.

Какой заряд установится на конденсаторе С ёмкостью 10 мкФ после замыкания ключа К в цепи, схема которой изображена на рисунке? Параметры цепи: В, Ом, Ом, Ом, Ом. Внутреннее сопротивление батареи равно нулю.

К задаче 3

Заряд легко отыщется, знай мы напряжение. Значит, давайте отыщем напряжение на конденсаторе.

Постоянный ток через конденсатор не течет, напряжение на нем будет равно

То есть наша задача – определить распределение токов в данной цепи (токи в ветвях). Причем даже не важно направление протекания тока, а важна его величина по модулю. Поэтому стрелки напряжений я расставила, даже не обратив внимания на источник, а по-хорошему можно было бы направить их в противоположные стороны. Но, повторюсь, на решение задачи это не влияет.

К задаче 3. Напряжения

Общее сопротивление

Тогда общий ток (в неразветвленной части) равен:

Напряжение на равно В, и столько же тогда падает на . Следовательно, токи

Тогда

Следовательно, заряд конденсатора равен

Ответ: мкКл.

Задача 4. Параллельный пучок света с длиной волны нм и концентрацией фотонов м нормально падает на идеальное зеркало, равномерно освещая всю его поверхность, площадь которой равна м. Чему равен модуль силы F давления этого светового пучка на зеркало?

Импульс фотона равен

Изменение же импульса равно

С другой стороны, .

В пучке много фотонов, их число равно . Определим, какой объем «покрывает» пучок за время :

Следовательно, на зеркало за падает число фотонов

Каждый из них изменит свой импульс, тогда

Ответ: мН

Источник

Тема 5.

Механика (изменение физических величин в процессах)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

механика (изменение физических величин в процессах)

5.01Кинематика

5.02Динамика

5.03Законы сохранения в механике

5.04Статика

5.05Гидростатика

5.06Механические колебания и волны

Решаем задачи

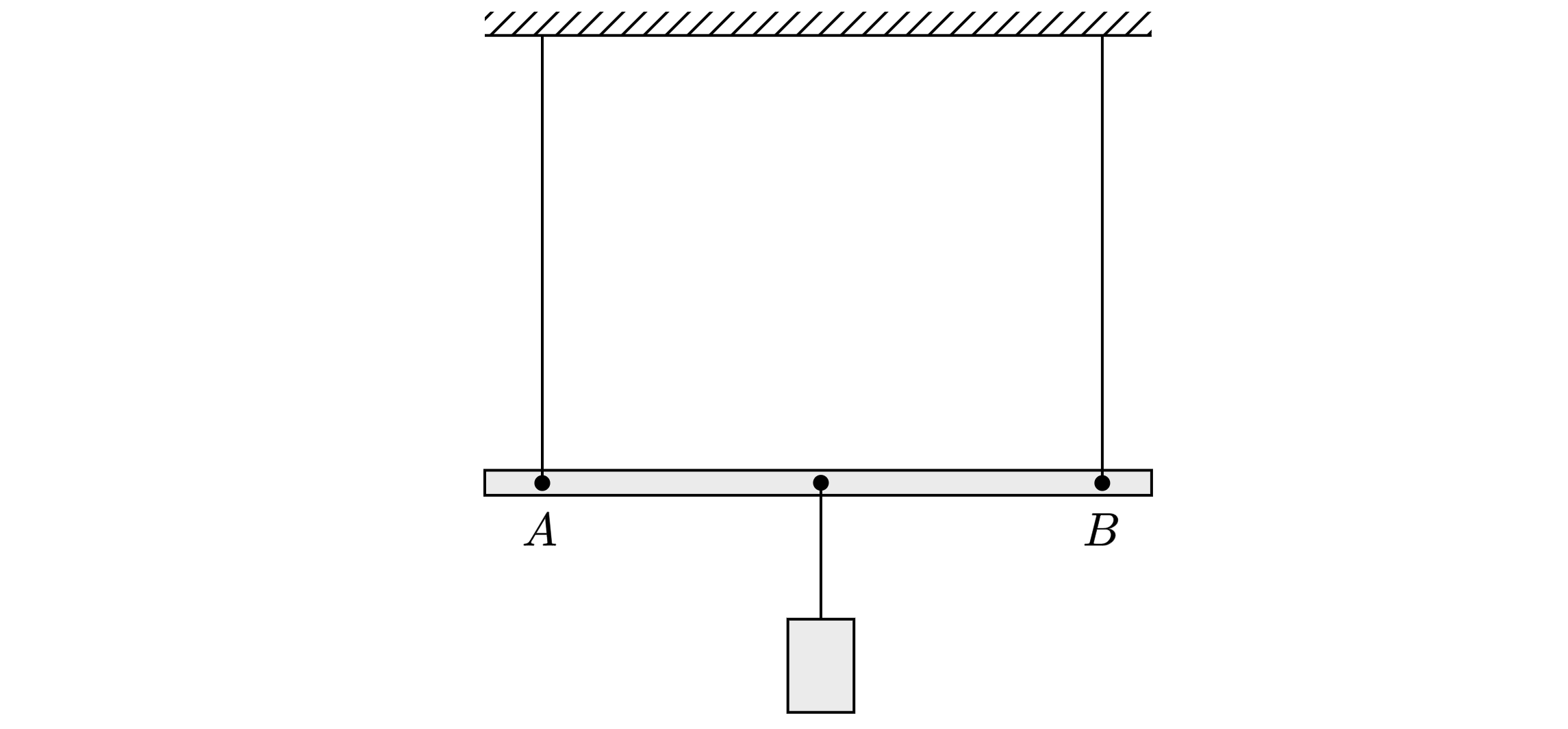
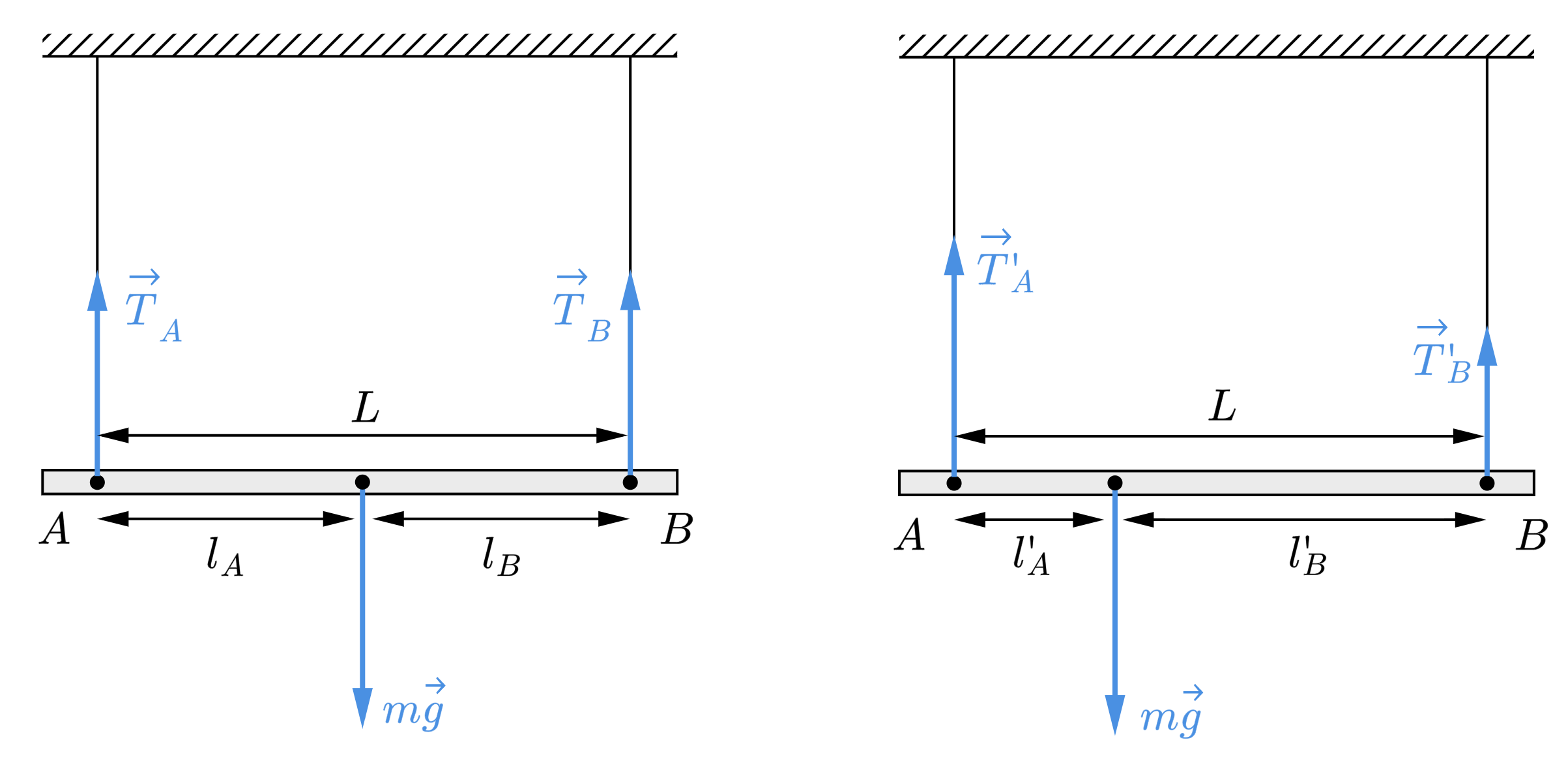
Лёгкий стержень подвешен в горизонтальном положении при помощи вертикальных нитей,
привязанных к его концам. К середине стержня подвешен груз. Груз перевешивают ближе к концу
стержня.

Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут
повторяться.

Показать ответ и решение

1) Ответ — 1.

Запишем правило моментов относительно точки :

Mmg = MT ⇒ mg ⋅ lA = TBL
B

После перевешивания груза ближе к точке сила тяжести не изменяется, плечо уменьшается
l′ < lA
A . Следовательно, сила натяжения правой нити уменьшается T ′ < TB
B .

По второму закону Ньютона . Так как сила натяжения правой нити уменьшается
и сила тяжести не изменяется, то сила натяжения T
A левой нити увеличивается.

2) Ответ — 2.

Момент действующей на груз силы тяжести относительно точки :

Так как при перевешивании груза ближе к точке плечо уменьшится l′ < lA
A , то и момент
действующей на груз силы тяжести относительно точки уменьшится.

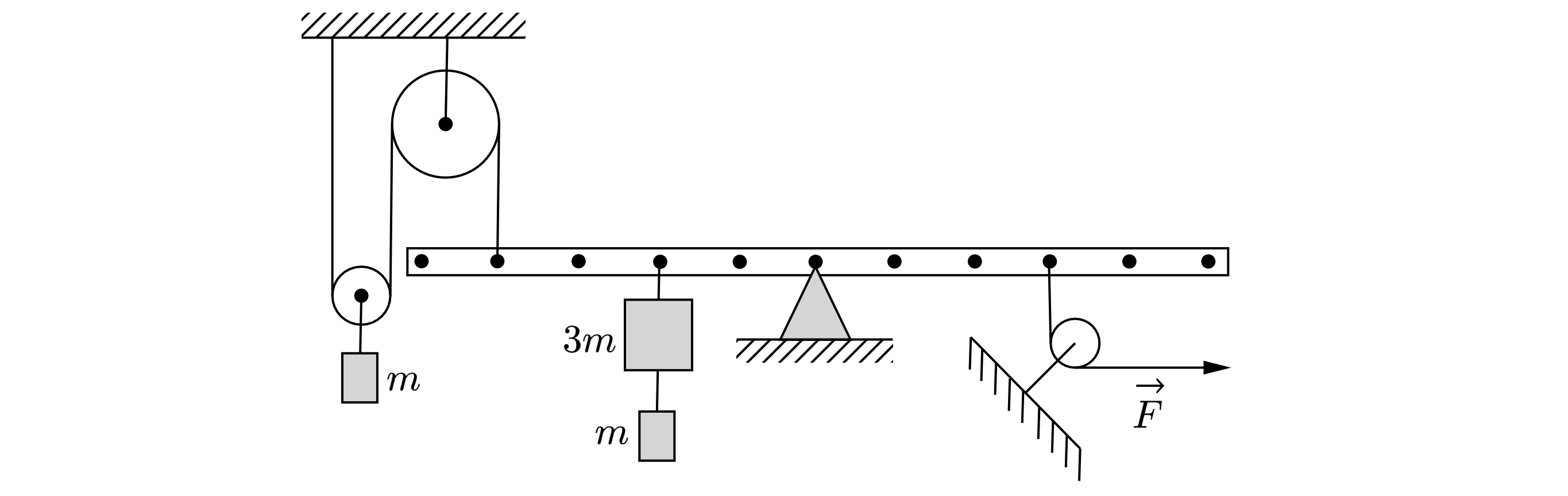
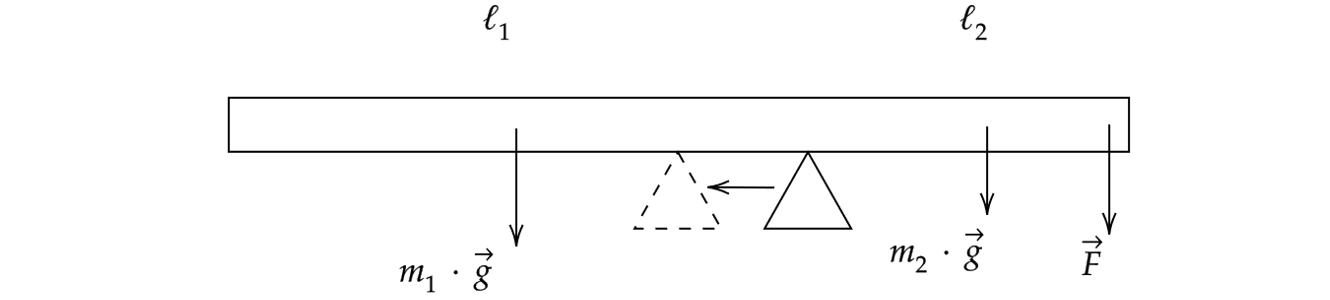
На лёгкой рейке при помощи постоянной силы уравновешены три груза массами , и (см.
рисунок). Трение в осях блоков отсутствует.

Правый груз массой отцепляют от груза массой и прикрепляют его к левому грузу массой
. Затем, перемещая точку приложения силы , опять уравновешивают рейку (модуль силы при
этом не меняется).

Определите, как в результате этого изменятся следующие физические величины: момент силы ;
суммарный момент сил, действующих на левую половину рейки.

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут
повторяться.

Однородная доска подперта на расстоянии 1/3 от её конца. К короткому концу перпендикулярно
приложена некоторая сила, удерживающая доску в равновесии. Как изменится минимальная
необходимая для удержания равновесия сила и момент силы длинного конца, если переместить точку
опоры на середину доски?

Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут
повторяться.

Показать ответ и решение

Момент силы длинного плеча можно найти по формуле

где
— масса длинной части доски, g — ускорение свободного падения, — длина большего плеча.
и m
1 уменьшаются, значит, M
1 также уменьшается.

Доска находится в равновесии, значит, можем записать правило моментов

M1 = m2 ⋅ g ⋅ ℓ2 + F ⋅ ℓ2,
2

где
— масса короткой части доски, — ускорение свободного падения, — длина малого плеча,
— прикладываемая сила. Отсюда выражаем

ℓ
M1 − m2 ⋅ g ⋅-2
F = -------------2--
ℓ2

уменьшается, ℓ
m2 ⋅ g ⋅-2
2 увеличивается, увеличивается, значит, уменьшается.

Груз необходимо удерживать в равновесии с помощью рычага, к правой стороне которого рабочий
прикладывает некоторую силу. Как изменится момент силы правого плеча и прикладываемая к нему
сила, если переместить ось вращения вправо?

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут
повторяться.

Показать ответ и решение

Момент силы левого плеча можно найти по формуле

где
— масса груза, — ускорение свободного падения, — длина левого плеча. увеличивается,
значит, вследствие прямой зависимости между величинами M
1 также увеличивается.
Система находится в равновесии, следовательно, по правилу моментов

где
— прикладываемая сила, — длина правого плеча. Выразим

ℓ1
F = m ⋅ g ⋅ ℓ
2

Масса не изменилась, увеличилось, уменьшилось, значит, F увеличилось.

Груз необходимо удерживать в равновесии с помощью рычага, к правой стороне которого рабочий
прикладывает некоторую силу. Как изменится момент силы левого плеча и сила, прикладываемая к
правому, если переместить ось вращения влево?

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут
повторяться.

Показать ответ и решение

Момент силы левого плеча можно найти по формуле

где
— масса груза, — ускорение свободного падения, — длина левого плеча. уменьшается,
значит, вследствие прямой зависимости между величинами M
1 также уменьшается.
Система находится в равновесии, следовательно, по правилу моментов

где
— прикладываемая сила, — длина правого плеча. Выразим

ℓ1
F = m ⋅ g ⋅ ℓ
2

Масса не изменилась, уменьшилось, увеличилось, значит, уменьшилась.

Источник

Общая информация об экзамене

ЕГЭ по физике состоит из 31 задания в двух частях.

Первая часть содержит 23 задания с кратким ответом:

13 заданий с кратким ответом в виде числа, слова или двух чисел
10 заданий на установление соответствия и множественный выбор

Вторая часть состоит из восьми заданий — решение задач. Для трех задач необходимо привести краткий ответ (задания с 24 по 26) и для пяти оставшихся заданий ответ должен быть развернутый (с решением).

В ЕГЭ по физике нас будут ждать следующие темы:

Механика (кинематика, динамика, статика, законы сохранения в механике, механические колебания и волны)
Молекулярная физика (молекулярно-кинетическая теория, термодинамика)
Электродинамика и основы СТО (электрическое поле, постоянный ток, магнитное поле, электромагнитная индукция, электромагнитные колебания и волны, оптика, основы СТО)
Квантовая физика (корпускулярно-волновой дуализм, физика атома, физика атомного ядра)

Общее количество заданий в экзаменационной работе по каждому из разделов приблизительно пропорционально его содержательному наполнению и учебному времени, отводимому на изучение данного раздела в школьном курсе физики.

Части работы	Количество заданий	Максимальный первичный бал	Тип заданий
1 часть	24	34	Краткий ответ
2 часть	8	18	Развернутый ответ
Итого	32	52

Время

На выполнение работы отводится 235 минут. Рекомендуемое время на выполнение заданий различных частей работы составляет:

для каждого задания с кратким ответом 3–5 минут
для каждого задания с развернутым ответом 15–25 минут

Источник

Вопрос. Подвижный блок. Опишите соотношение сил и перемещений при использовании подвижного блока.

Задача. Система из двух легких прочных тросов, двух неподвижных и двух подвижных блоков и двух грузов подвешена к потолку (см. рисунок). Все блоки  — легкие и вращаются без трения, тросы по блокам не скользят. Конец одного из тросов закреплен на шкиве выключенной лебедки, груз 2 удерживают на месте. Этот груз аккуратно отпускают, а затем почти сразу включают лебедку, которая начинает вытягивать трос с постоянной скоростью За какое время груз 2 поднимется на высоту Отношение масс грузов Временем разгона грузов и их смещением при разгоне пренебречь.

Спрятать решение

Решение.

Ответ на вопрос. Подвижный блок  — простой механизм (показан на рисунке). При смещении свободного конца веревки, перекинутой через подвижный блок, оно поровну распределяется между двумя сторонами петли, и смещение оси блока будет в два раза меньше, чем смещение конца веревки: При плавном равномерном движении блока (или если масса блока пренебрежимо мала при конечных ускорениях) сумма сил, приложенных к блоку, должна равняться нулю, и для легкой веревки сила, приложенная к оси блока, будет в два раза больше силы, натягивающей веревку: В результате подвижный блок не дает выигрыша в работе:

Решение задачи. Направим координатную ось x вертикально вниз. Движение, согласно условию, начинается таким образом, что грузы в процессе разгона движутся под действием сил натяжения нитей. Если рассмотреть «верхний» из подвижных блоков, то, как следует из ответа, мы придем к выводу, что сила натяжения «левой» нити T_1 в два раза больше, чем «правой» Уравнения движения грузов, следующие из II закона Ньютона, имеют вид:

и C учетом соотношения масс обнаруживается, что в процессе разгона то есть (начальные скорости обоих грузов равны нулю). Сумма длин вертикальных отрезков (левой» нити в процессе движения системы после разгона должна уменьшаться со скоростью u, а сумма длин вертикальных отрезков «правой»  — оставаться неизменной. Поэтому координаты грузов x_1,2 и координата верхнего блока должны удовлетворять соотношениям и Следовательно, const Значит, изменения этих координат за малое время Delta t связаны соотношением и проекции скоростей грузов на ось x тоже связаны: Таким образом, при t=0 скорости грузов

Так как скорости и дальше должны быть связаны этим соотношением при одинаковых ускорениях, то эти ускорения равны нулю, и скорости будут оставаться постоянными! Об этом можно было догадаться и без прямого вычисления, если обратить внимание, что при выключенной лебедке грузы находятся в равновесии. Итак, груз 2 поднимается вверх со скоростью Поэтому искомое время подъема

Ответ:

Спрятать критерии

Критерии проверки:

Классификатор: Механика. Движение связанных тел

Источник