СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Треугольники и их элементы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 27289
В треугольнике ABC
Найдите
Аналоги к заданию № 27289: 520479 520499 520520 520543 31891 31893 31895 31897 31899 31901 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
1 комментарий · Сообщить об ошибке · Помощь
2
Тип 12 № 27290
В треугольнике ABC
Найдите
Аналоги к заданию № 27290: 19283 19285 19287 19289 19291 19293 19295 19297 19299 19301 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 12 № 27303
высота CH равна 4,
Найдите
Аналоги к заданию № 27303: 32499 32501 32503 32505 32507 32509 32511 32513 32515 32517 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 12 № 27309
В треугольнике ABC
высота CH равна 20. Найдите
Аналоги к заданию № 27309: 4563 4565 4567 4569 4571 4573 Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 12 № 27619
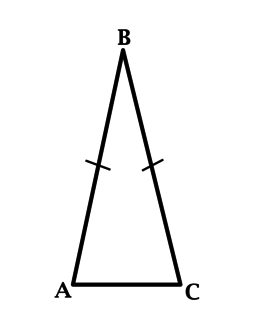
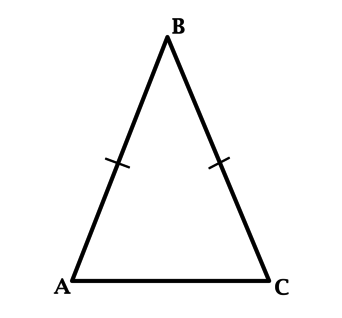
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Аналоги к заданию № 27619: 26342 56555 56557 56559 56561 56563 56565 56567 56569 56571 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
Геометрия на плоскости (планиметрия)
Задание
1
#199
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 81^{circ}), (angle C = 25^{circ}). Найдите внешний угол при вершине (A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle B + angle C =) внешнему углу при вершине (A), следовательно (A_{text{внеш}}) ( = 81^{circ} + 25^{circ} = 106^{circ}).
Ответ: 106
Задание
2
#200
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 22^{circ}), внешний угол при вершине (C) равен (130^{circ}). Найдите (angle B). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle A + angle B = C_{text{внеш}}), тогда (22^{circ} + angle B = 130^{circ}), откуда находим (angle B = 130^{circ} — 22^{circ} = 108^{circ}).
Ответ: 108
Задание
3
#201
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 35^{circ}), внешний угол при вершине (B) равен (91^{circ}). Найдите (angle A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle C + angle A = B_{text{внеш}}), тогда (35^{circ} + angle A = 91^{circ}), откуда находим (angle A = 91^{circ} — 35^{circ} = 56^{circ}).
Ответ: 56
Задание
4
#202
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 70^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 70^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 70^{circ} — 70^{circ} = 40^{circ}).
Ответ: 40
Задание
5
#203
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 47^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle A = 47^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 47^{circ} — 47^{circ} = 86^{circ}).
Ответ: 86
Задание
6
#204
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 36^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 36^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 36^{circ} — 36^{circ} = 108^{circ}).
Ответ: 108
Задание
7
#205
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 38^{circ}), (AB = BC). Найдите (angle C). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C). Так как у любого треугольника сумма углов равна (180^{circ}), то (180^{circ} = 38^{circ} + angle A + angle C = 38^{circ} + 2cdot angle A), откуда (2cdot angle A = 142^{circ}), тогда (angle A = 71^{circ}).
Ответ: 71
Геометрические задачи ЕГЭ с решениями
Суббота, 3 сентября, 2016
В данной статье разобраны решения геометрических задач, встречающихся в вариантах профильного ЕГЭ по математике. Всего таких задач 5: 3 из первой части и 2 из второй. По крайней мере, такой расклад был на момент написания статьи. Представленные материалы будут полезны тем, кто только начал подготовку к предстоящему экзамену. Здесь вы найдёте геометрические задачи ЕГЭ с решениями, снабжёнными подробными и понятными комментариями от профессионального репетитора по математике. Представлен также видеоразбор решений каждого задания.
Задачи представлены под номерами, под которыми они числятся в вариантах профильного ЕГЭ по математике.
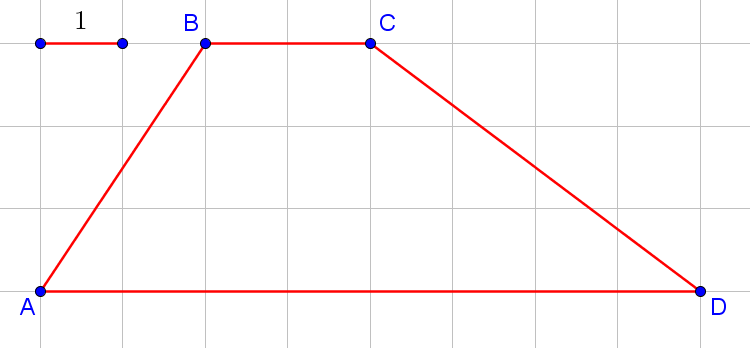
Задача 3. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
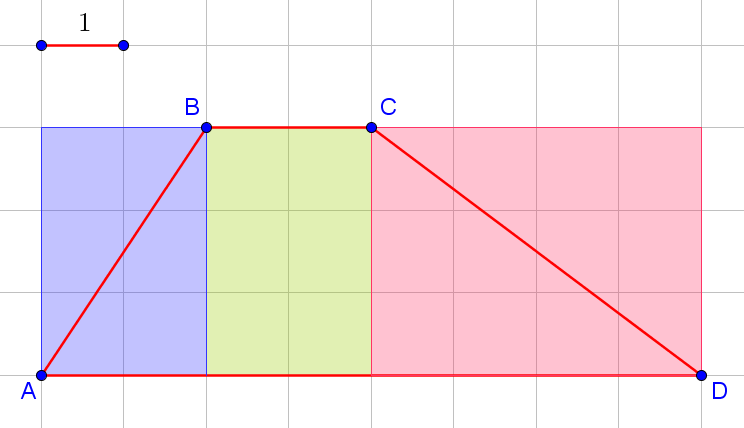
Даже если вы забыли формулу площадь трапеции на экзамене, не спешите отчаиваться. Вы всегда может решить задачу проще, чем вас научили в школе. В данном случае можно просто посчитать площадь по клеточкам:
Искомая площадь равна половине площади синего прямоугольника, плюс площади зелёного прямоугольника, плюс половина площади красного прямоугольника. Итого, получаем .
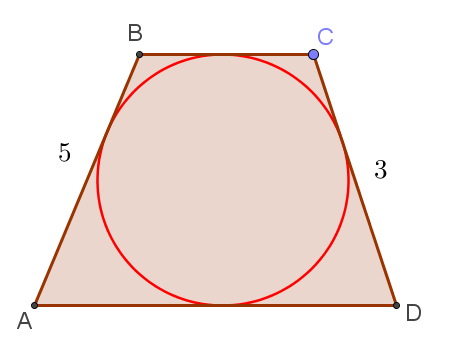
Задача 6. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
По-хорошему, рисунок здесь не нужен. Поскольку в трапецию вписана окружность, то суммы противоположных сторон равны. Следовательно, сумма оснований равна 8, а полусумма и, соответственно, средняя линия трапеции равны 4.
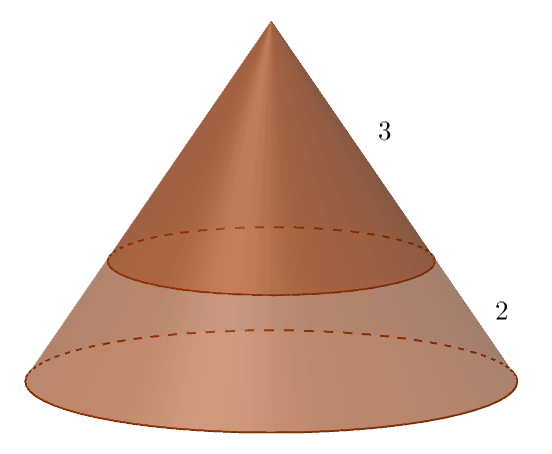
Все линейные размеры малого конуса в раз отличаются от линейных размеров большого конуса. Следовательно, квадратичные размеры (площадь поверхности) малого конуса в
раз отличаются от квадратичных размеров большого конуса. То есть искомая площадь полной поверхности отсечённого конуса равна
.
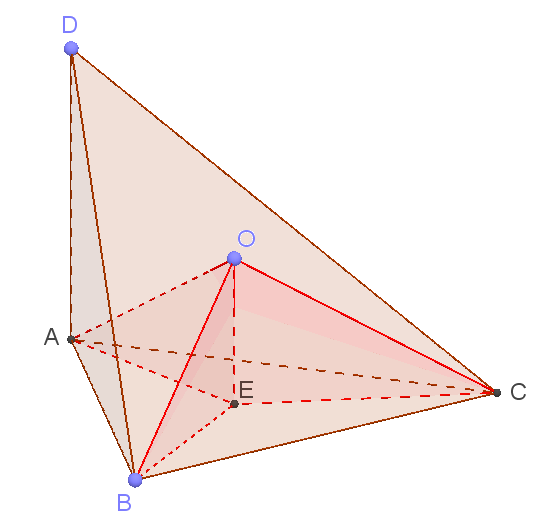
а) Докажите, что прямая, проходящая через точку O и центр описанной около треугольника ABC окружности, перпендикулярна плоскости ABC.
б) Найдите радиус описанной сферы, если AB = 6, а AD = 4.
а) Из точки O опустим перпендикуляр OE на плоскость ABC:
Точка O равноудалена от точек A, B и C, так как O — центр описанной около пирамиды окружности. Тогда выделенные красным цветом прямоугольные треугольники AOE, BOE и COE равны по гипотенузе и катету.
Тогда AE = BE = CE. То есть точка E, лежащая в плоскости треугольника ABC, равноудалена от его вершин. Следовательно, она является центром описанной около него окружности. Что и требовалось доказать.
При доказательстве мы использовали так называемый метод решения с конца. Построили требуемый перпендикуляр и доказали, что данные условия задачи удовлетворены.
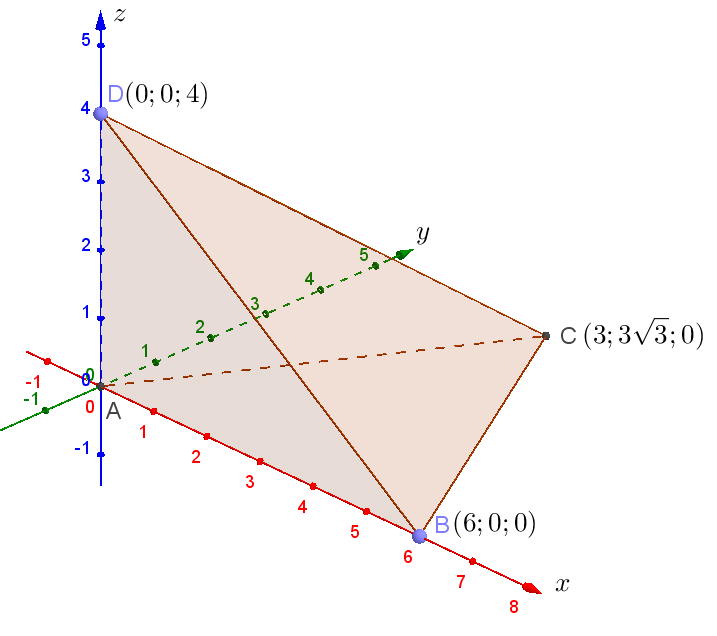
б) Введем систему координат, как показано на рисунке, и определим координаты вершин пирамиды в этой системе:
Пусть центр описанной около этой пирамиды сферы имеет координаты . Пусть радиус сферы равен
. Тогда уравнение сферы во введённой системе координат имеет вид:
Этой сфере принадлежат все вершины данной пирамиды. Следовательно, имеет место следующая система:
Сравнивая первые два уравнения, получаем , откуда
. Аналогично, сравнивая первое и третье уравнения, получаем
, откуда
.
Теперь подставляем полученные значения в первое и последнее уравнение. В результате приходим к системе:
Вычитаем почленно из первого уравнения второе и получаем:
Тогда из первого уравнения получаем, что , откуда
. Отрицательное значение не берём, так как радиус не может быть отрицателен.
Обратите внимание, что попутно мы также получили координаты центра описанной сферы .
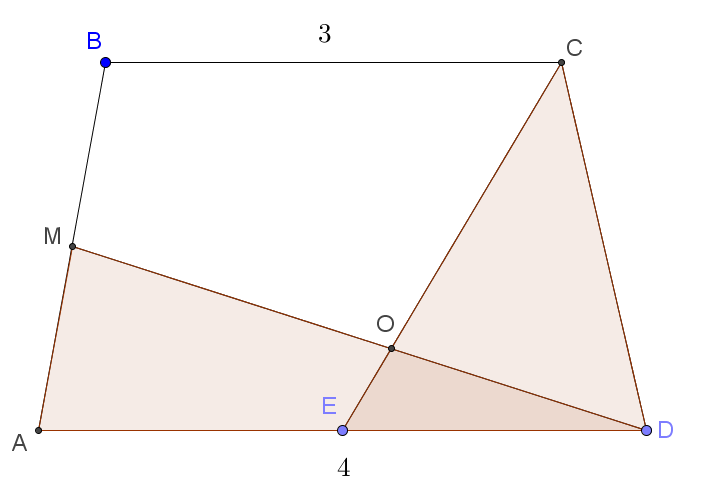
a) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Изобразим чертёж к задаче:
а) Высота треугольника AMD из вершины M вдвое меньше высоты треугольника ECD из вершины C. При этом основание AD вдвое больше основания ED. Значит площади этих треугольников равны. А поскольку EOD — общая часть этих этих треугольников, то площади четырёхугольника AMOE и треугольника COD равны.
б) Обозначим высоту трапеции за . Тогда её площадь равна
кв. ед., а площадь треугольника AMD равна
кв. ед. Цель состоит в том, чтобы найти площадь треугольника EOD.
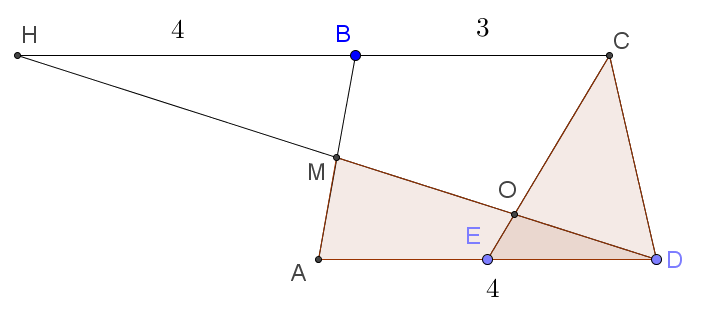
Выполним дополнительное построение: продолжим отрезок MD до пересечения с прямой BC в точке H. Тогда рисунок будет выглядеть следующим образом:
Треугольник HMB равен треугольнику AMD по стороне и двум прилежащим к ней углам. Следовательно, HB равно 4. Треугольник HCO подобен треугольнику ODE по двум углам. При этом коэффициент подобия равен .
Следовательно, высота треугольника OEA, проведенная к основанию ED, равна . Тогда площадь четырёхугольника AMOE равна
кв. ед. Тогда искомое отношение равно
.
Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем
Смотрите также:
- Задачи на доказательство геометрических фактов из ГИА;
- Разбор заданий первой части профильного ЕГЭ по математике;
- Разбор задачи 14 профильного ЕГЭ по математике.
Задача 3. Начала теории вероятностей
Задача 3. Начала теории вероятностей
Задача 4. Вероятности сложных событий
Задача 4. Вероятности сложных событий
Задача 5. Простейшие уравнения
Задача 5. Простейшие уравнения
Задача 6. Вычисления и преобразования
Задача 6. Вычисления и преобразования
Задача 7. Производная и первообразная
Задача 7. Производная и первообразная
Задача 8. Задачи с прикладным содержанием
Задача 8. Задачи с прикладным содержанием
Задача 9. Текстовые задачи
Задача 9. Текстовые задачи
Задача 10. Графики функций
Задача 10. Графики функций
Задача 11. Наибольшее и наименьшее значение функций
Задача 11. Наибольшее и наименьшее значение функций
По теме: методические разработки, презентации и конспекты
Решение стереометрической задачи тремя различными способами
Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…
Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…
Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…
Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.
Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…
- Угол между двумя прямыми
Задача 1, Задача 2.
- Угол между прямой и плоскостью
Задача1. Задача 2.
- Угол между двумя плоскостями
Задача 1. Задача 2.
- Расстояние от точки до прямой
Задача 1. Задача 2.
- Расстояние от точки до плоскости
Задача 1. Задача 2.
- Расстояние между скрещивающимися прямыми
Задача 1. Задача 2.
1.Определение: Две пересекающиеся прямые образуют смежные и вертикальные углы.
Углом между двумя прямыми называется меньший из них.
Угол между перпендикулярными прямыми равен 90°. Угол между параллельными прямыми равен 0°.
С 1
D 1
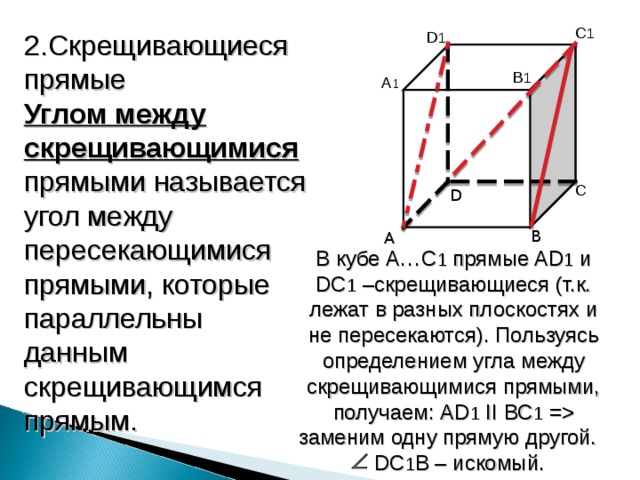
2.Скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
B 1
А 1
С
D
В
А
В кубе A…C 1 прямые AD 1 и DC 1 –скрещивающиеся (т.к. лежат в разных плоскостях и не пересекаются). Пользуясь определением угла между скрещивающимися прямыми, получаем: AD 1 II BC 1 = заменим одну прямую другой. DC 1 B – искомый.
.
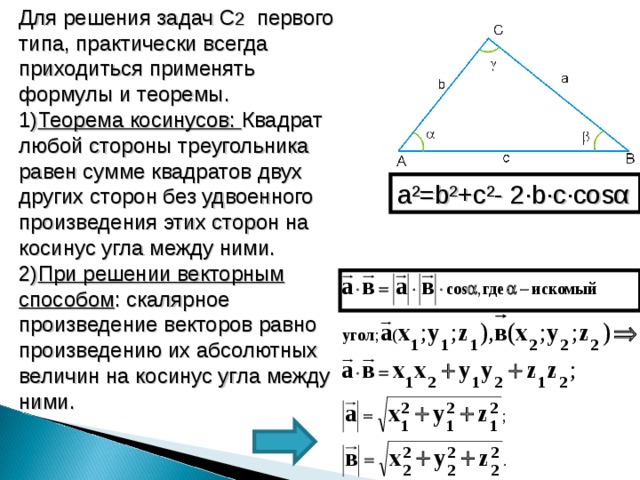
Для решения задач C 2 первого типа, практически всегда приходиться применять формулы и теоремы.
- Теорема косинусов: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
- При решении векторным способом : скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
a²=b² + c²- 2∙b∙c∙cos α
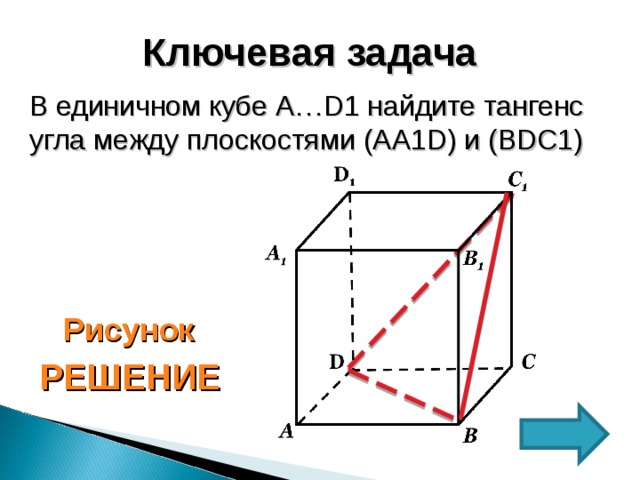
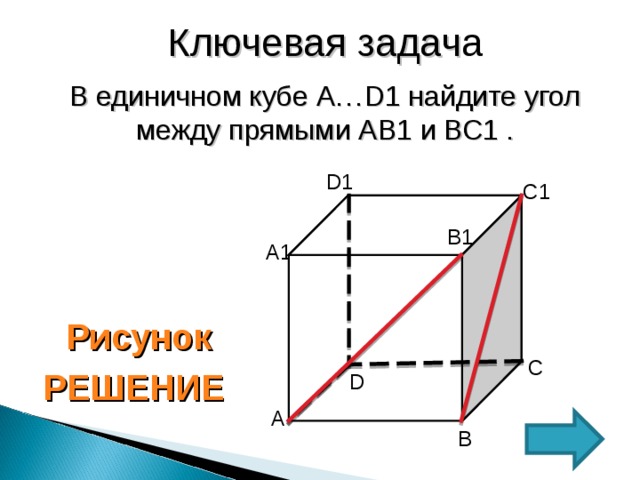
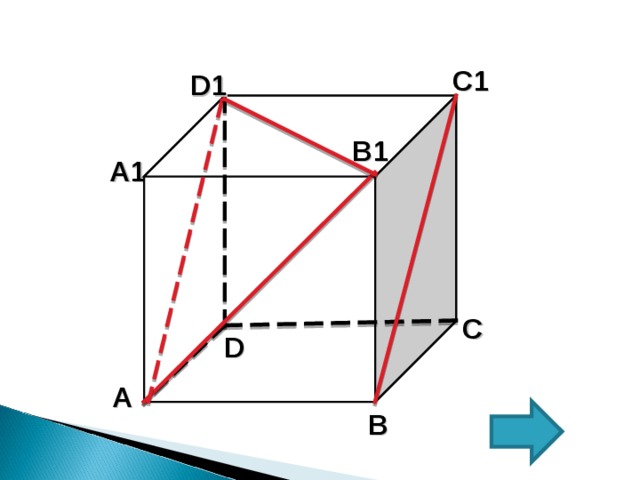
Ключевая задач а
В единичном кубе А… D 1 найдите угол между прямыми АВ1 и ВС1 .
D 1
C 1
B 1
А1
Рисунок
С
РЕШЕНИЕ
D
А
В
6
С1
D 1
B 1
А1
С
D
А
В
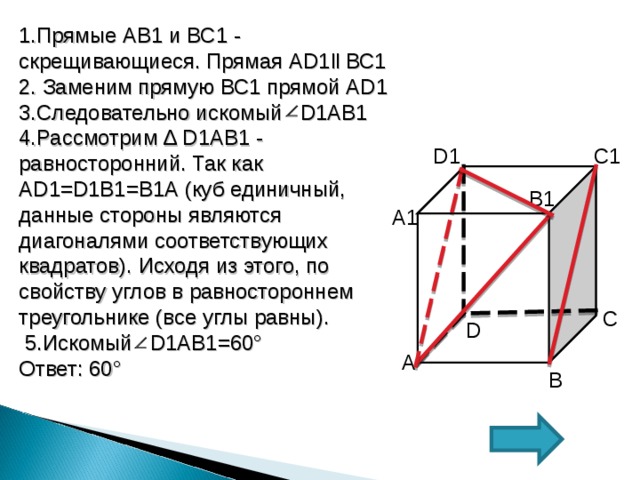
1.Прямые АВ1 и ВС1 — скрещивающиеся. Прямая А D 1 ll ВС1
2. Заменим прямую ВС1 прямой А D 1
3.Следовательно искомый D 1АВ1
4.Рассмотрим ∆ D 1АВ1 — равносторонний. Так как А D 1= D 1В1=В1А (куб единичный, данные стороны являются диагоналями соответствующих квадратов). Исходя из этого, по свойству углов в равностороннем треугольнике (все углы равны).
5.Искомый D 1АВ1=60°
Ответ: 60°
C 1
D 1
B 1
А1
С
D
А
В
8
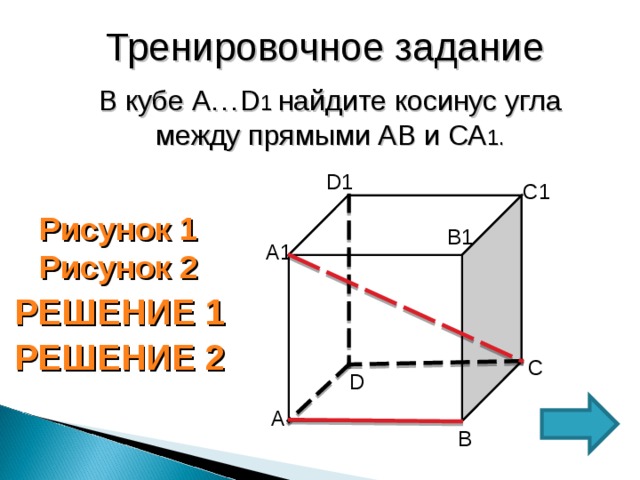
Тренировочное задание
В кубе А… D 1 найдите косинус угла между прямыми АВ и СА 1.
D 1
C 1
Рисунок 1
Рисунок 2
B 1
А1
РЕШЕНИЕ 1
РЕШЕНИЕ 2
С
D
А
В
D 1
C 1
B 1
А1
С
D
А
В
C 1
D 1
B 1
А1
С
D
А
В
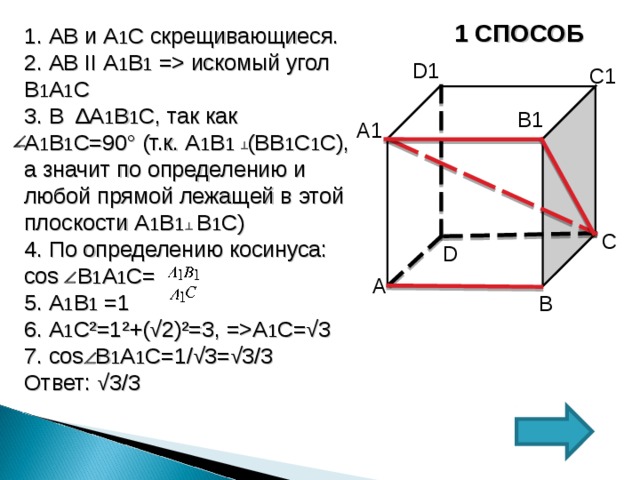
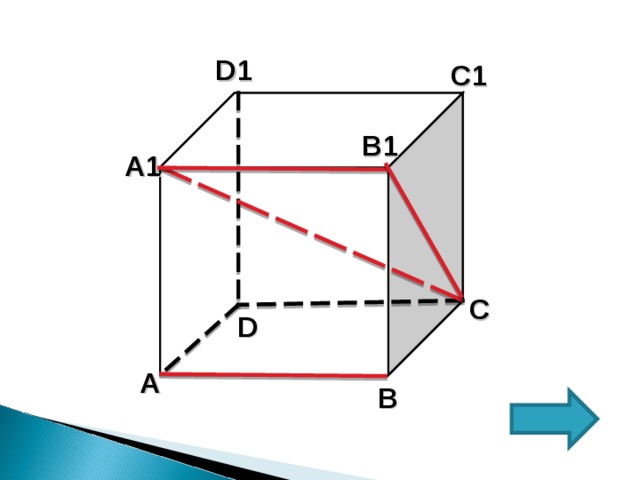
1 СПОСОБ
1. АВ и А 1 С скрещивающиеся.
2. АВ II А 1 В 1 = искомый угол В 1 А 1 С
3. В ∆А 1 В 1 С, так как
А 1 В 1 С=90° (т.к. А 1 В 1 (ВВ 1 С 1 С), а значит по определению и любой прямой лежащей в этой плоскости А 1 В 1 В 1 С)
4. По определению косинуса:
cos В 1 А 1 С=
5. А 1 В 1 =1
6. А 1 С²=1²+(√2)²=3, =А 1 С=√3
7. с os В 1 А 1 С=1/√3=√3/3
Ответ: √3/3
D 1
C 1
B 1
А1
С
D
А
В
12
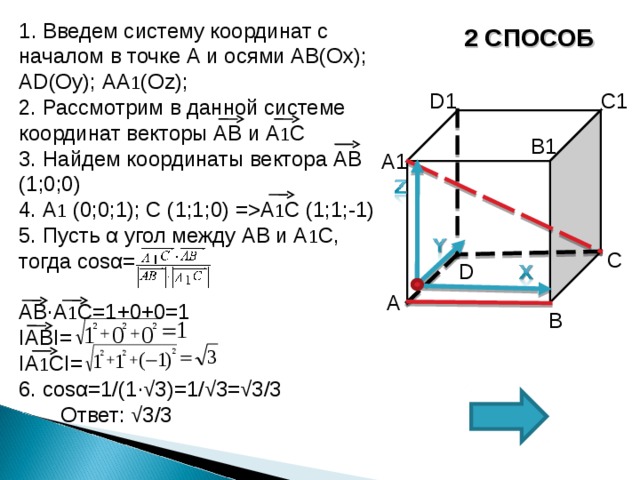
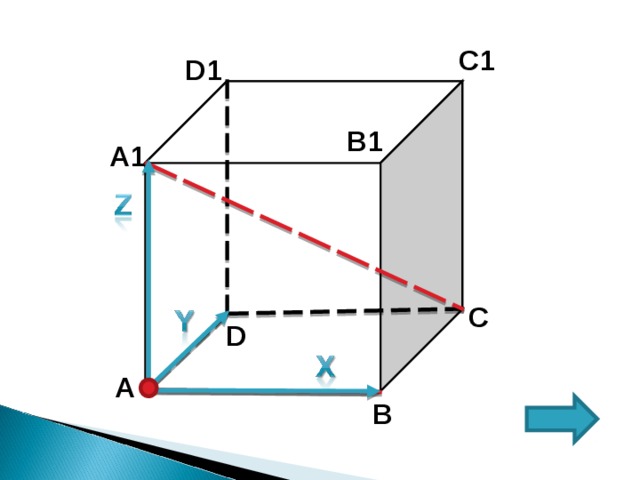
1 . Введем систему координат с началом в точке А и осями АВ(Ох); А D (Оу); АА 1 (О z );
2. Рассмотрим в данной системе координат векторы АВ и А 1 С
3. Найдем координаты вектора АВ (1;0;0)
4. А 1 (0;0;1); С (1;1;0) =А 1 С (1;1;-1)
5. Пусть α угол между АВ и А 1 С,
тогда cos α =
АВ∙А 1 С=1+0+0=1
I АВ I =
I А 1 С I =
6. с os α =1/(1∙√3)=1/√3=√3/3
Ответ: √3/3
2 СПОСОБ
C 1
D 1
B 1
А1
С
D
А
В
1 . Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
2. Угол между взаимно перпендикулярными прямой и плоскостью равен 90 .
3. Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0 .
В
а
С
α י
А
α
а ∩ α =А
ВС α
ВАС – искомый угол
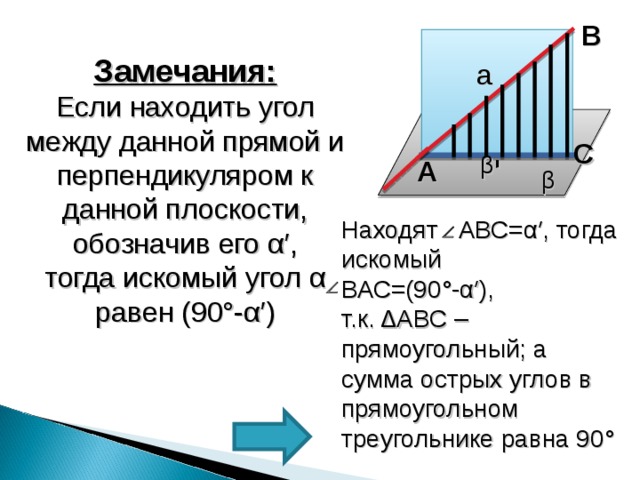
Замечания:
Если находить угол между данной прямой и перпендикуляром к данной плоскости, обозначив его α′ ,
тогда искомый угол α равен (90°- α′ )
В
а
С
β י
А
β
Находят АВС= α′ , тогда искомый ВАС=(90°- α′ ),
т.к. ∆АВС – прямоугольный; а сумма острых углов в прямоугольном треугольнике равна 90°
Ключевая задача
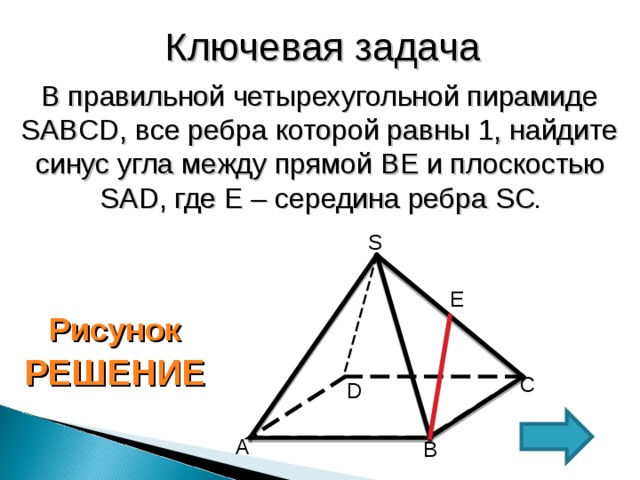
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD , где Е – середина ребра SC .
S
E
Рисунок
РЕШЕНИЕ
C
D
А
B
S
F
E
S
C
D
А
B
E
F
К
S 1
C
B
H
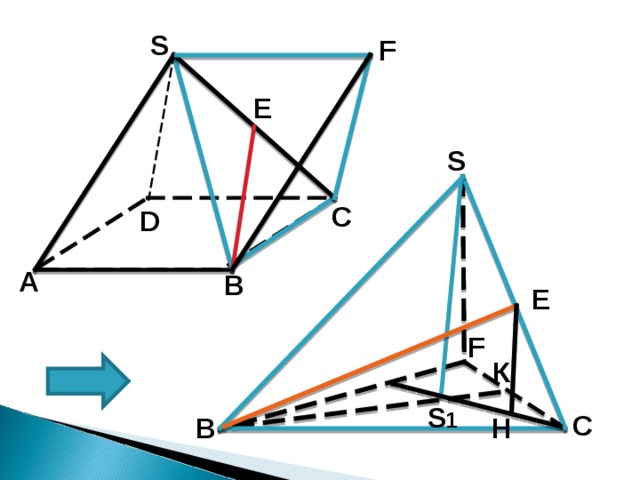
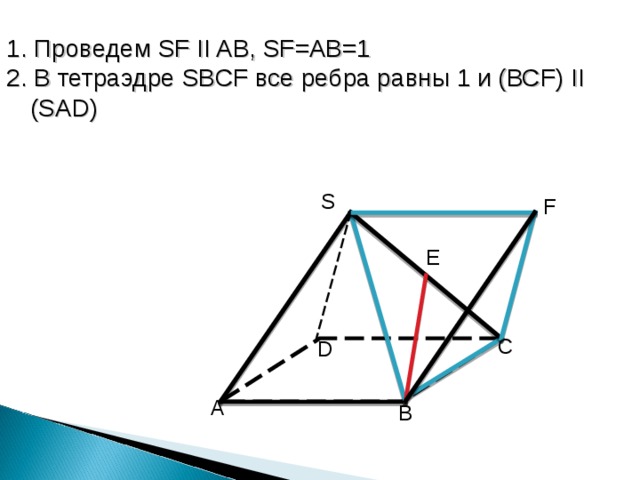
1. Проведем SF II AB , SF = AB =1
2. В тетраэдре SB С F все ребра равны 1 и (ВС F) II (SAD)
S
F
E
C
D
А
B
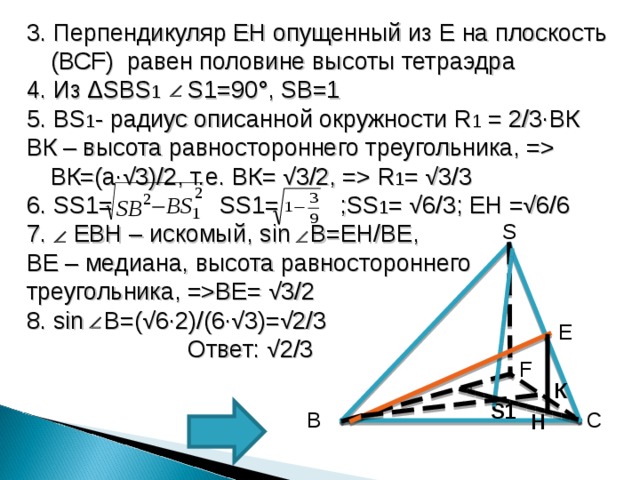
3. Перпендикуляр EH опущенный из Е на плоскость (ВС F) равен половине высоты тетраэдра
4. Из ∆ SBS 1 S 1=90°, SB =1
5. BS 1 — радиус описанной окружности R 1 = 2/3∙ B К
B К – высота равностороннего треугольника, = B К=(а∙√3)/2, т.е. B К= √3/2, = R 1 = √3/3
6. SS1= SS1= ; SS 1 = √6/3 ; EH =√6/6
7. EBH – искомый, sin B=EH/BE ,
BE – медиана, высота равностороннего
треугольника, = BE = √3/2
8. sin B =(√6∙2)/(6∙√3)=√2/3
Ответ: √2/3
S
E
F
К
S1
B
C
H
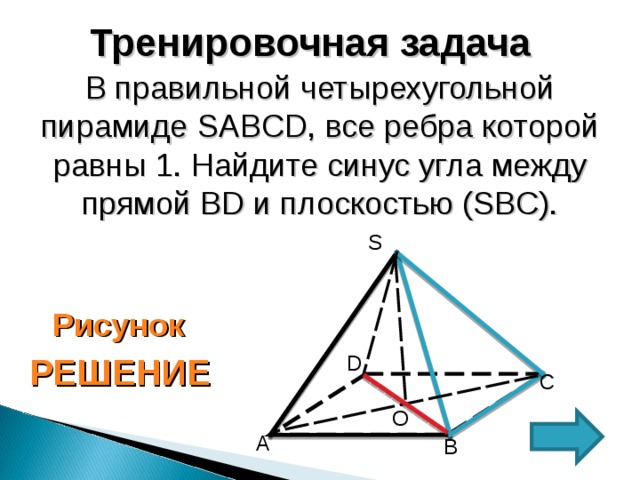
Тренировочная задача
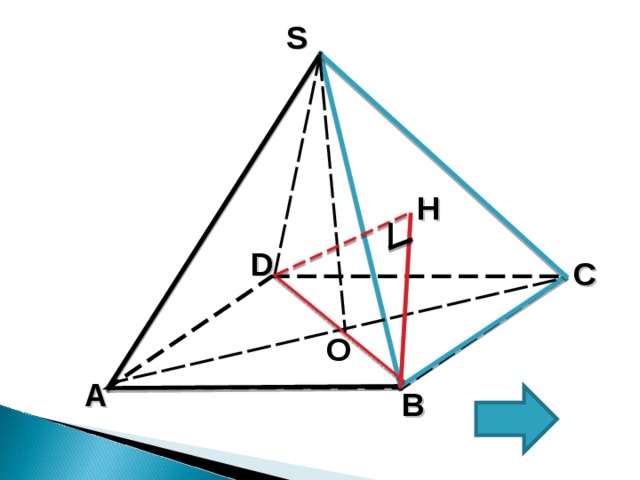
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите синус угла между прямой BD и плоскостью (SBC).
S
Рисунок
D
РЕШЕНИЕ
C
O
А
B
S
H
D
C
O
А
B
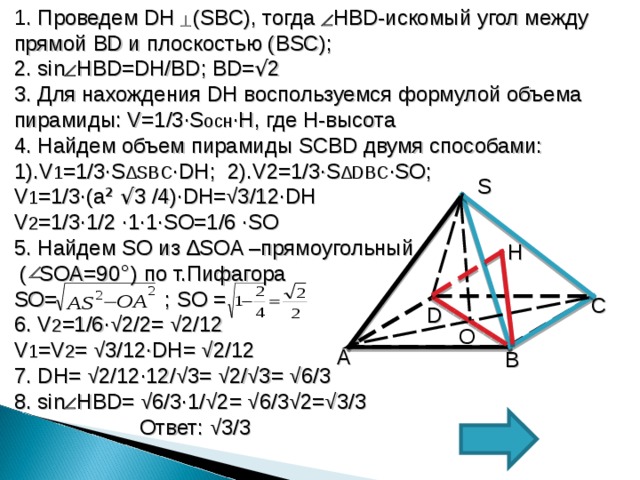
1 . Проведем DH (SBC) , тогда HBD -искомый угол между прямой BD и плоскостью ( BSC) ;
2. sin HBD=DH/BD ; BD= √ 2
3. Для нахождения DH воспользуемся формулой объема пирамиды: V=1/3∙S осн ∙ H , где H -высота
4. Найдем объем пирамиды SCBD двумя способами:
1). V 1 =1/3∙S ∆ SBC ∙DH ; 2). V2=1/3∙S ∆ DBC ∙SO ;
V 1 =1/3∙ ( a ² √ 3 /4 ) ∙DH= √ 3/12∙DH
V 2 =1/3∙1/2 ∙ 1 ∙1∙SO=1/6 ∙SO
5. Найдем SO из ∆ SOA –прямоугольный
( SOA=90 ° ) по т.Пифагора
SO= ; SO =
6. V 2 =1/6∙ √ 2/2= √ 2/12
V 1 =V 2 = √ 3/12∙DH= √ 2/12
7. DH= √ 2/12∙12/ √ 3= √ 2/ √ 3= √ 6/3
8. sin HBD= √ 6/3∙1/ √ 2= √ 6/3 √ 2= √ 3/3
Ответ: √ 3/3
S
H
C
D
O
А
B
Двугранный угол , образованный полуплоскостями измеряется величиной его линейного угла,
получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
Величина двугранного угла принадлежит промежутку (0°; 180°).
Величина угла между пересекающимися плоскостями принадлежит промежутку (0°; 90°].
Угол между двумя параллельными плоскостями равен 0° .
Ключевая задача
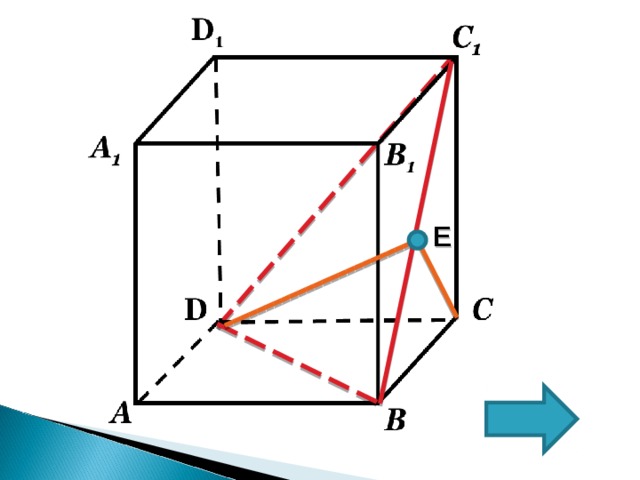
В единичном кубе А…D1 найдите тангенс угла между плоскостями (АА1D) и (BDC1)
Рисунок
РЕШЕНИЕ
E
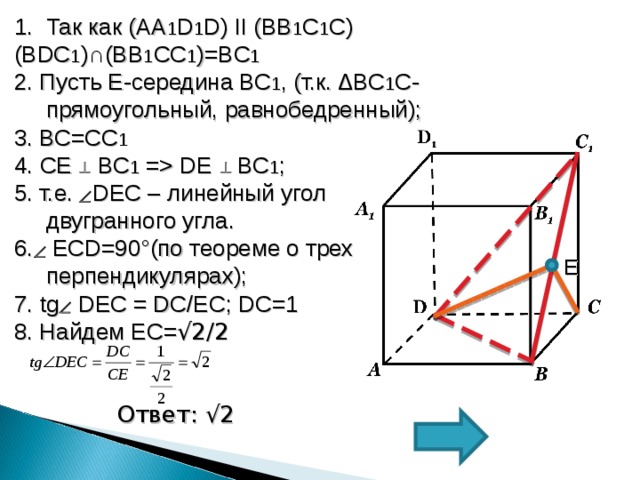
- Так как (АА 1 D 1 D) II ( BB 1 C 1 С)
( BDC 1 )∩(BB 1 CC 1 )=BC 1
2. Пусть Е-середина ВС 1 , (т.к. ∆ BC 1 C- прямоугольный, равнобедренный);
3. ВС=С C 1
4. CE BC 1 = DE BC 1 ;
5. т.е. DEC – линейный угол двугранного угла.
6. ECD=90°( по теореме о трех перпендикулярах);
7. tg DEC = DC/EC ; DC=1
8. Найдем EC = √2/2
Ответ: √2
E
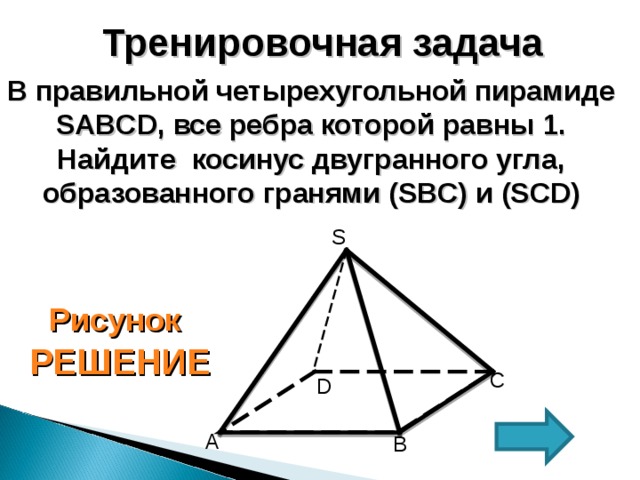
Тренировочная задача
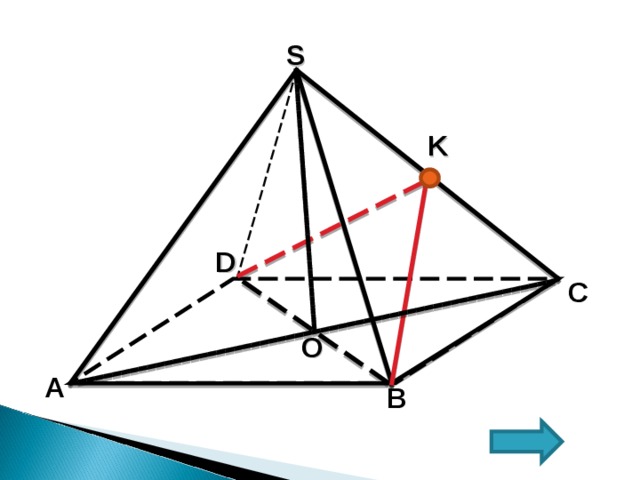
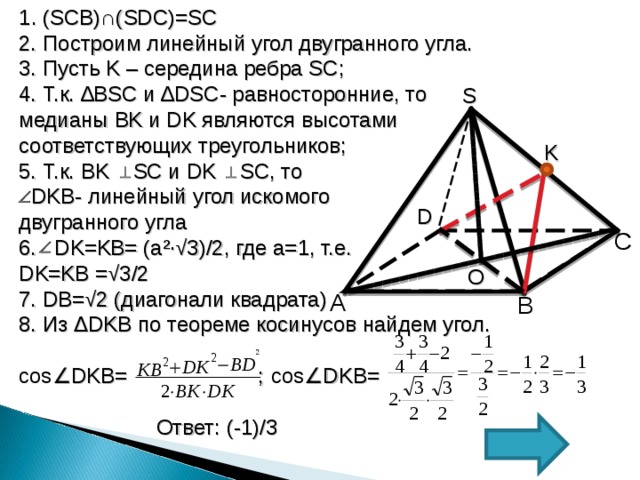
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите косинус двугранного угла, образованного гранями ( SBC) и (SCD)
S
Рисунок
РЕШЕНИЕ
C
D
А
B
S
K
D
С
O
А
B
1 . (SCB)∩(SDC)=SC
2. Построим линейный угол двугранного угла.
3. Пусть K – середина ребра SC ;
4. Т.к. ∆BSC и ∆ DSC — равносторонние, то медианы BK и DK являются высотами соответствующих треугольников;
5. Т.к. BK SC и DK SC , то
DKB- линейный угол искомого
двугранного угла
6. DK=KB= (a²∙√3)/2 , где а=1, т.е.
DK=KB =√3/2
7. DB=√2 (диагонали квадрата)
8. Из ∆ DKB по теореме косинусов найдем угол.
cos ∠ DKB= ; cos ∠ DKB=
Ответ: (-1)/3
S
K
D
C
O
А
B
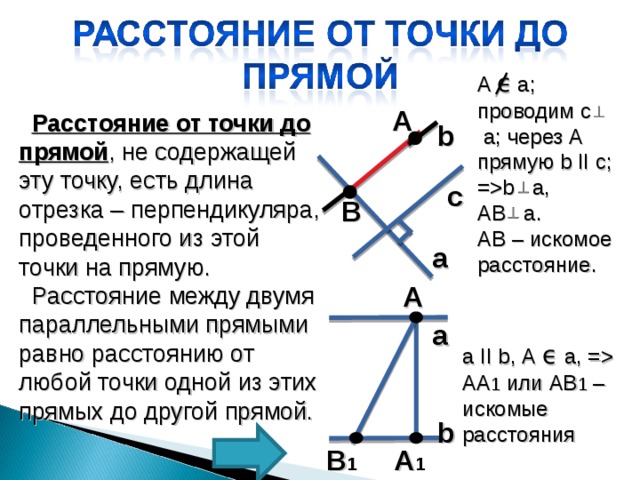
A ϵ а; проводим с
а; через А прямую b II с; = b a ,
AB а .
AB – искомое расстояние.
A
Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка – перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
b
с
B
a
A
a
a II b, А ϵ а, = АА 1 или АВ 1 – искомые расстояния
b
A 1
B 1
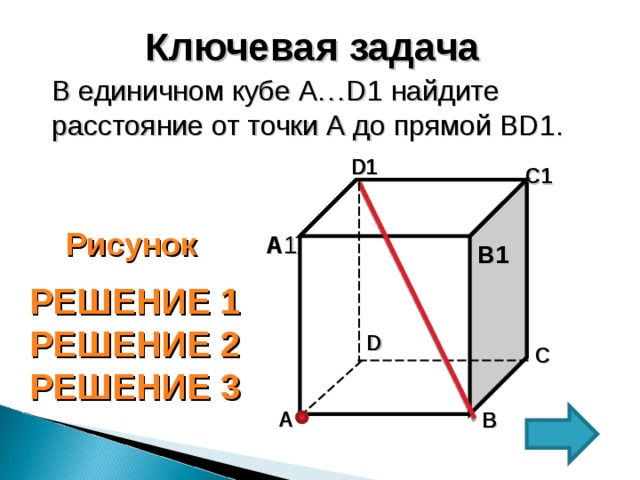
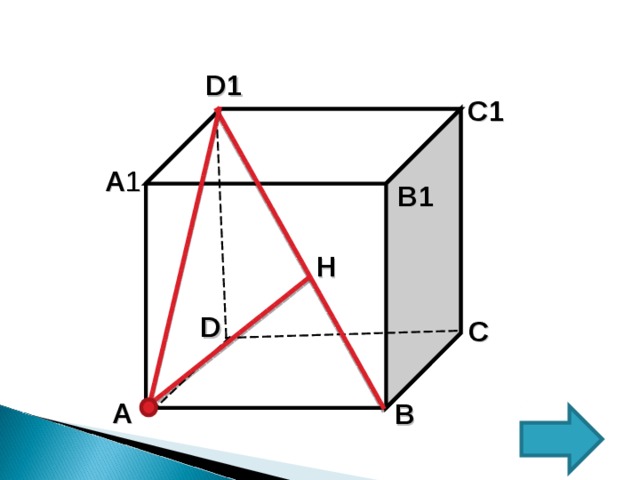
Ключевая задача
В единичном кубе А…D 1 найдите расстояние от точки А до прямой BD 1 .
D
D 1
C 1
Рисунок
A 1
B 1
РЕШЕНИЕ 1
РЕШЕНИЕ 2
РЕШЕНИЕ 3
D
C
A
B
B
D 1
С1
A 1
B 1
H
D
C
A
B
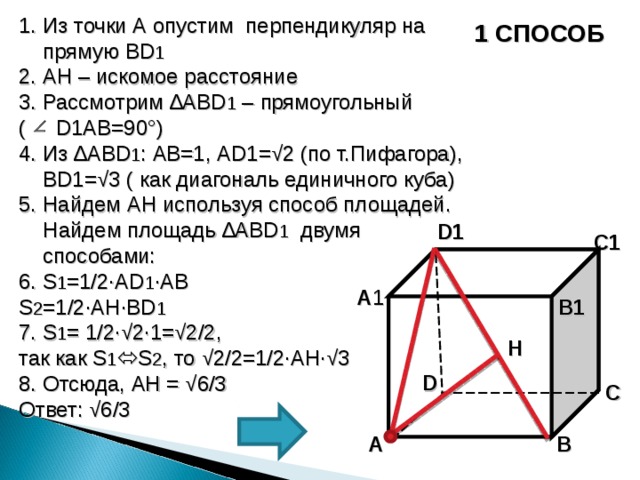
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D1AB =90°)
4. Из ∆ ABD 1 : AB =1, AD1 =√2 (по т.Пифагора), BD1 =√3 ( как диагональ единичного куба)
5. Найдем AH используя способ площадей. Найдем площадь ∆ ABD 1 двумя способами:
6. S 1 =1/2∙AD 1 ∙AB
S 2 =1/2∙AH∙BD 1
7. S 1 = 1/2∙√2∙1=√2/2 ,
так как S 1 S 2 , то √2/2=1/2∙AH∙√3
8. Отсюда, AH = √ 6/3
Ответ: √6/3
1 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
A
B
30
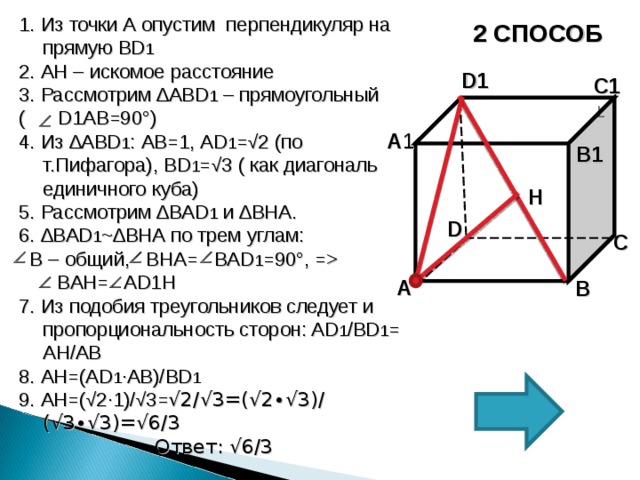
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D1AB =90°)
4. Из ∆ ABD 1 : AB =1, AD 1 =√2 (по т.Пифагора), BD 1 =√3 ( как диагональ единичного куба)
5. Рассмотрим ∆ BAD 1 и ∆ BHA .
6. ∆ BAD 1 ~ ∆ BHA по трем углам:
B – общий, BHA= BAD 1 =90°, =
BAH= AD1H
7. Из подобия треугольников следует и пропорциональность сторон: AD 1 /BD 1 = AH/AB
8 . AH =( AD 1 ∙AB )/ BD 1
9. А H = ( √ 2∙1)/√3= √2/√3=(√2∙√3)/(√3∙√3)=√6/3
Ответ: √6/3
2 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
H
A
B
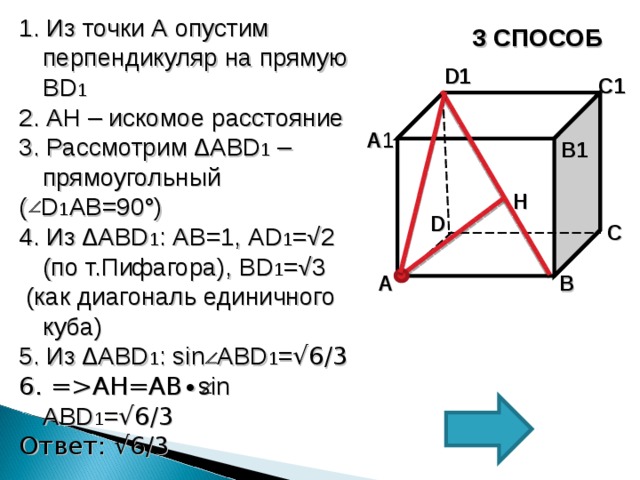
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D 1 AB =90°)
4. Из ∆ ABD 1 : AB =1, AD 1 =√2 (по т.Пифагора), BD 1 =√3
(как диагональ единичного куба)
5. Из ∆ ABD 1 : sin ABD 1 = √6/3
6 . = AH=AB∙ sin ABD 1 = √6/3
Ответ: √6/3
3 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
A
B
Тренировочное задание
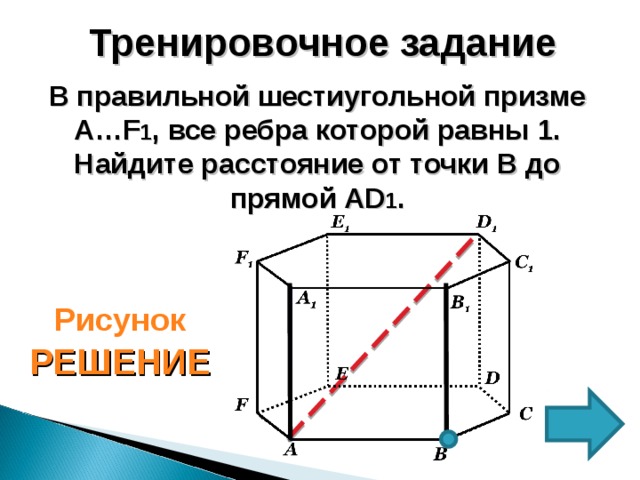
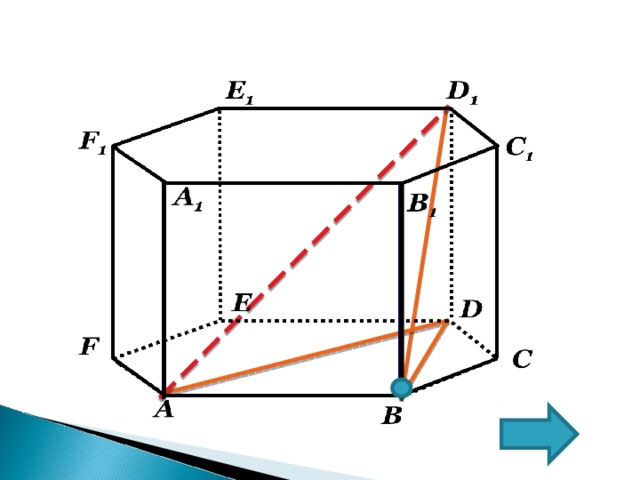
В правильной шестиугольной призме A…F 1 , все ребра которой равны 1. Найдите расстояние от точки B до прямой AD 1 .
Рисунок
РЕШЕНИЕ
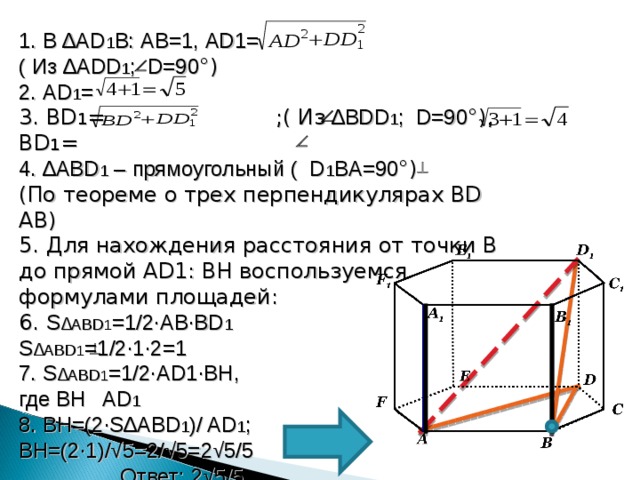
1. В ∆ AD 1 B : AB=1 , AD1=
( Из ∆ ADD 1 ; D=90 °)
2. AD 1 =
3. BD 1 = ;( Из ∆ BDD 1 ; D=90 °) , BD 1 =
4. ∆ ABD 1 – прямоугольный ( D 1 BA=90 °)
( По теореме о трех перпендикулярах BD AB)
5. Для нахождения расстояния от точки В до прямой AD1 : BH воспользуемся формулами площадей:
6. S ∆ ABD 1 =1/2∙AB∙BD 1
S ∆ ABD 1 =1/2∙1∙2=1
7. S ∆ ABD 1 =1/2∙AD1∙BH ,
где BH AD 1
8. BH=(2∙S ∆ ABD 1 )/ AD 1 ;
BH=(2∙1)/√5=2/√5=2√5/5
Ответ: 2√5/5
A
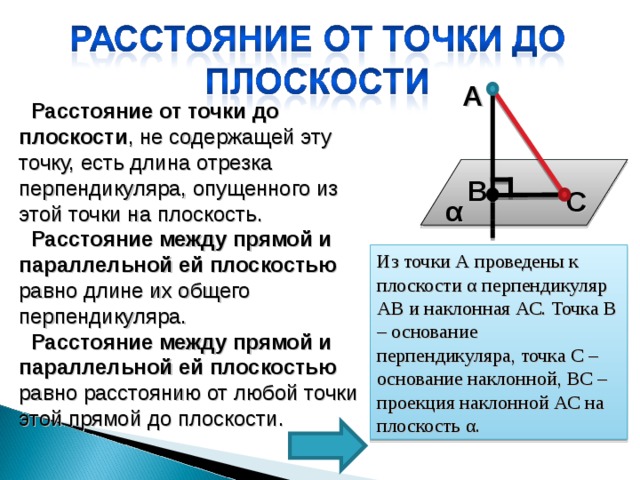
Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
B
C
α
Из точки А проведены к плоскости α перпендикуляр АВ и наклонная АС. Точка В – основание перпендикуляра, точка С – основание наклонной, ВС – проекция наклонной АС на плоскость α .
А
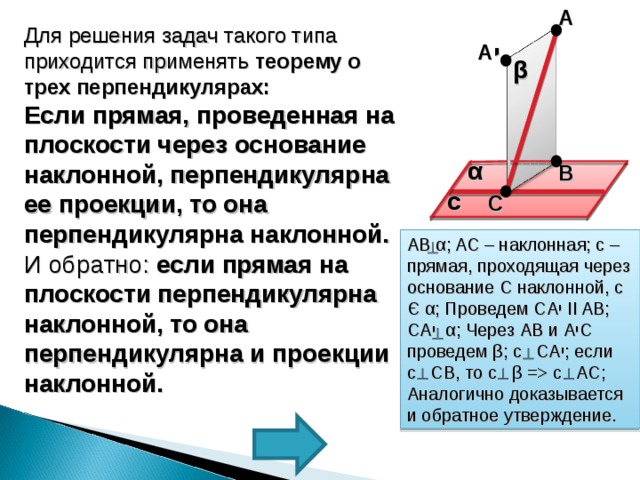
Для решения задач такого типа приходится применять теорему о трех перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
A י
β
α
B
c
C
AB α ; AC – наклонная; с – прямая, проходящая через основание С наклонной, с Є α ; Проведем С A י II AB ; С A י α ; Через AB и A י С проведем β ; с СА י ; если
с СВ, то с β = с АС;
Аналогично доказывается и обратное утверждение.
Ключевая задача
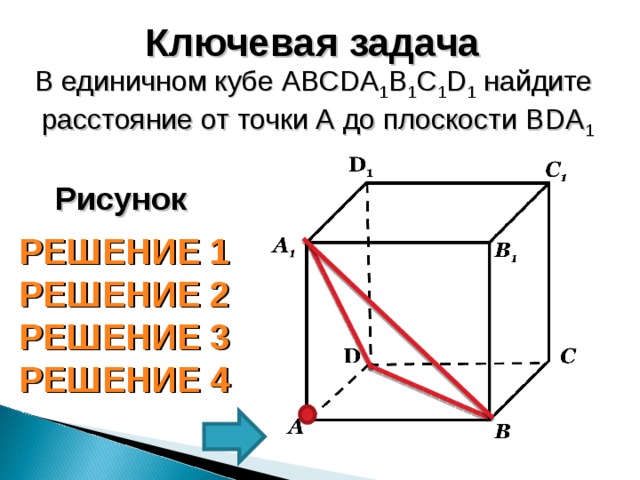
В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите
расстояние от точки А до плоскости В D А 1
Рисунок
РЕШЕНИЕ 1
РЕШЕНИЕ 2
РЕШЕНИЕ 3
РЕШЕНИЕ 4
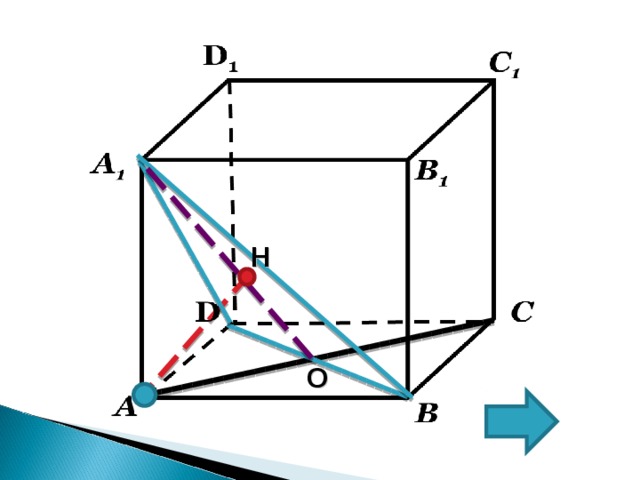
H
O
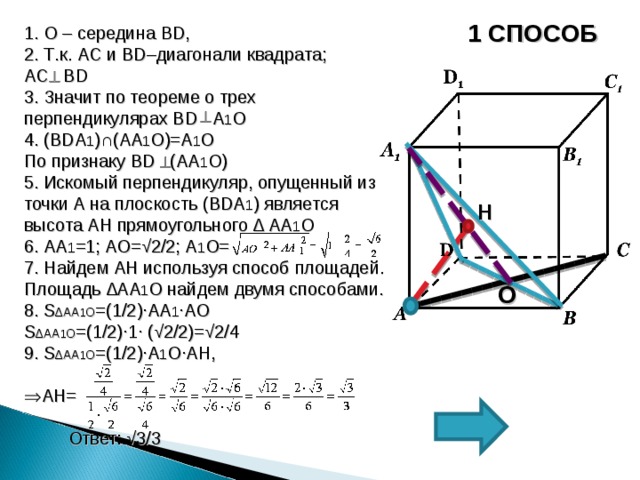
1 СПОСОБ
1. О – середина BD ,
2. Т . к. AC и BD –диагонали квадрата;
AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного ∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Найдем А H используя способ площадей.
Площадь ∆АА 1 О найдем двумя способами.
8. S ∆АА 1 О =(1/2)∙ АА 1 ∙ А O
S ∆АА 1 О =(1/2)∙1∙ ( √ 2/2)=√2/4
9. S ∆АА 1 О =(1/2)∙ А 1 О ∙ А H ,
- А H=
Ответ: √3/3
H
О
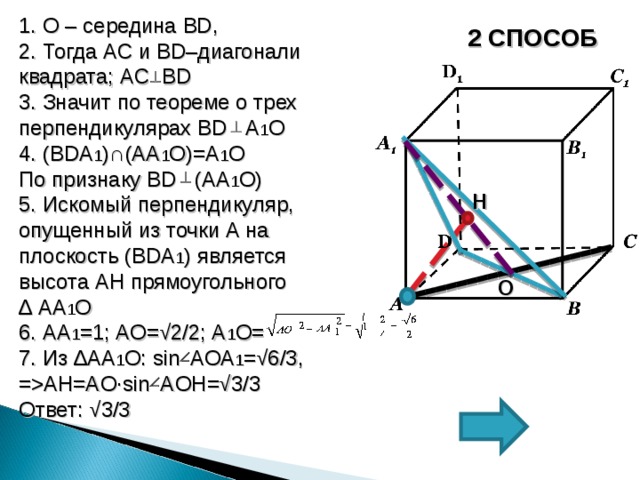
1. О – середина BD ,
2. Тогда AC и BD –диагонали квадрата; AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного
∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Из ∆ A А 1 О: sin A ОА 1 =√6/3 ,
= AH=A О ∙sin A О H=√ 3 /3
Ответ: √ 3 /3
2 СПОСОБ
H
О
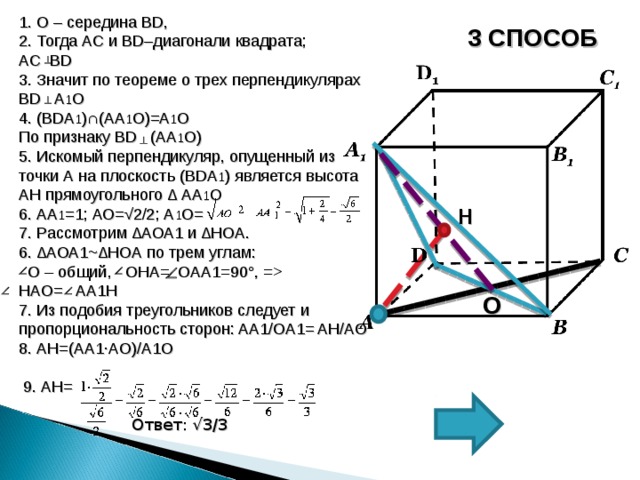
1. О – середина BD ,
2. Тогда AC и BD –диагонали квадрата;
AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного ∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Рассмотрим ∆АОА 1 и ∆ H О A .
6. ∆АОА 1~ ∆ H О A по трем углам:
О – общий, О HA= О A А 1=90°, = HA О = A А 1H
7. Из подобия треугольников следует и пропорциональность сторон: A А 1/ ОА 1= AH/A О
8 . AH =( A А 1∙A О)/А 1 О
9. А H =
Ответ: √3/3
3 СПОСОБ
H
О
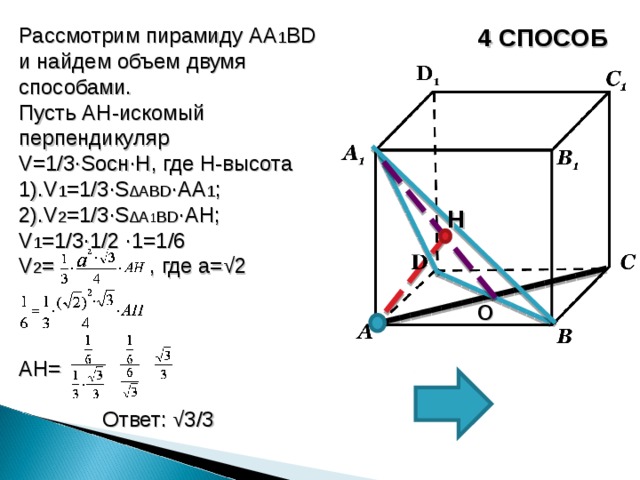
Рассмотрим пирамиду AA 1 BD и найдем объем двумя способами.
Пусть AH -искомый перпендикуляр
V=1/3∙S осн∙ H , где H -высота
1). V 1 =1/3∙S ∆А BD ∙AA 1 ; 2). V 2 =1/3∙S ∆ A 1 BD ∙AH ;
V 1 =1/3∙1/2 ∙ 1 =1/6
V 2 = , где а=√2
AH =
Ответ: √3/3
4 СПОСОБ
H
О
Тренировочная задача
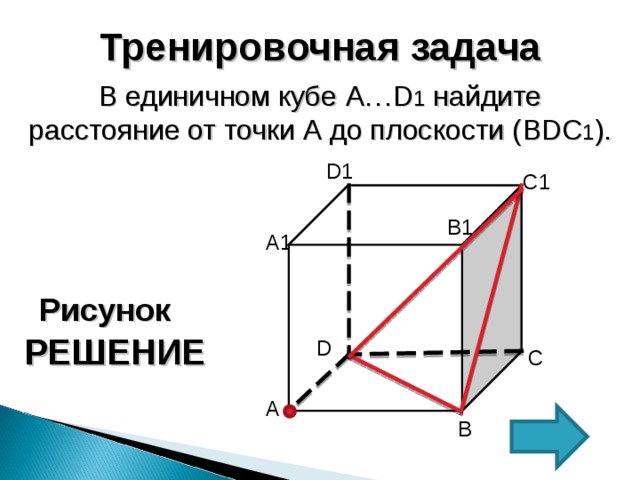
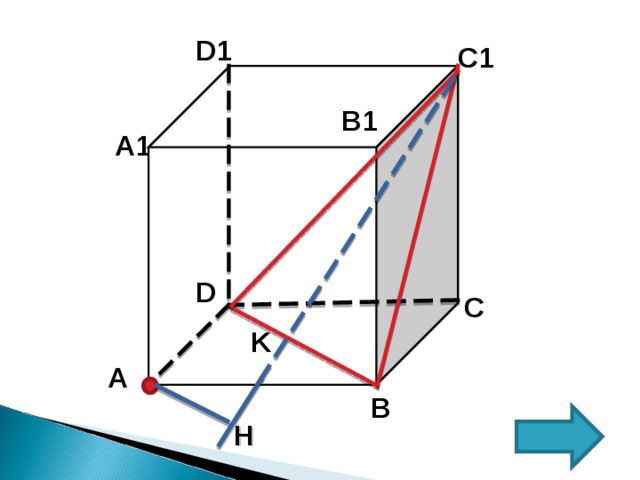
В единичном кубе A … D 1 найдите расстояние от точки А до плоскости ( BDC 1 ).
D1
C1
B1
А 1
Рисунок
РЕШЕНИЕ
D
С
А
В
D1
C1
B1
А 1
D
С
K
А
В
H
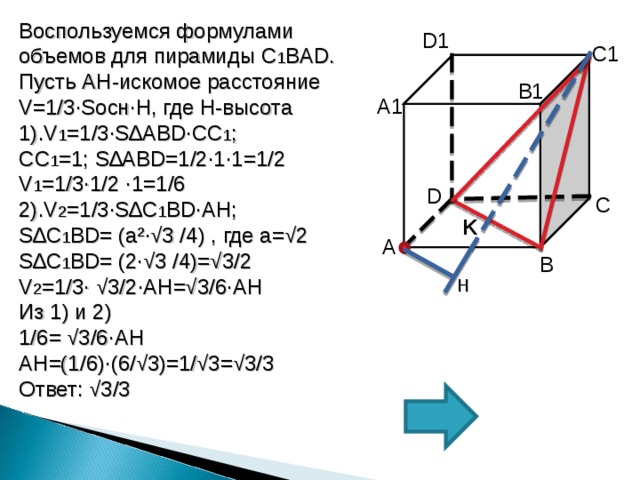
Воспользуемся формулами объемов для пирамиды C 1 BAD .
Пусть AH -искомое расстояние
V=1/3∙S осн∙ H , где H -высота
1). V 1 =1/3∙S ∆А BD∙ СС 1 ;
СС 1 =1; S ∆А BD =1/2∙1∙1=1/2
V 1 =1/3∙1/2 ∙ 1 =1/6
2). V 2 =1/3∙S ∆С 1 BD∙AH ;
S ∆С 1 BD = ( a² ∙√ 3 /4 ) , где а=√2
S ∆С 1 BD = (2∙√ 3 /4 )=√3/2
V 2 =1/3∙ √3/2 ∙AH =√3/6 ∙AH
Из 1) и 2)
1/6= √3/6 ∙AH
AH =(1/6)∙(6/√3)=1/√3=√3/3
Ответ: √3/3
D1
C1
B1
А 1
D
С
K
А
В
H
β
А
а
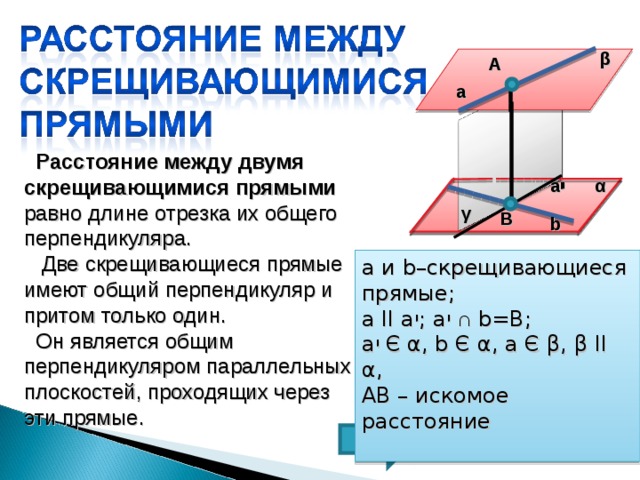
Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.
Две скрещивающиеся прямые имеют общий перпендикуляр и притом только один.
Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
а י
α
γ
В
b
а и b –скрещивающиеся прямые;
а II а י ; а י ∩ b=B ;
a י Є α , b Є α , a Є β , β II α ,
АВ – искомое расстояние
Ключевая задача
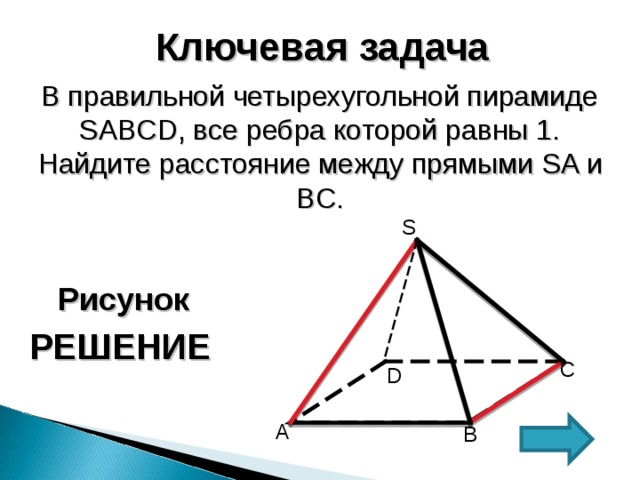
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите расстояние между прямыми SA и BC .
S
Рисунок
РЕШЕНИЕ
C
D
А
B
S
H
D
C
E
F
O
А
B
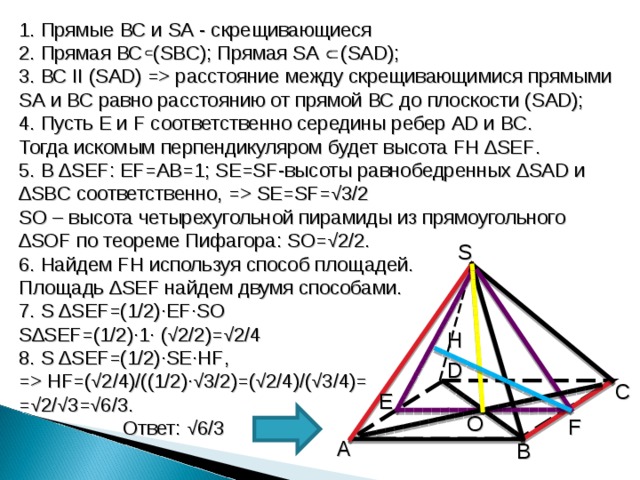
1. Прямые ВС и SA — скрещивающиеся
2. Прямая ВС ( SBC ); Прямая SA ( SAD );
3. ВС II ( SAD ) = расстояние между скрещивающимися прямыми SA и ВС равно расстоянию от прямой ВС до плоскости ( SAD );
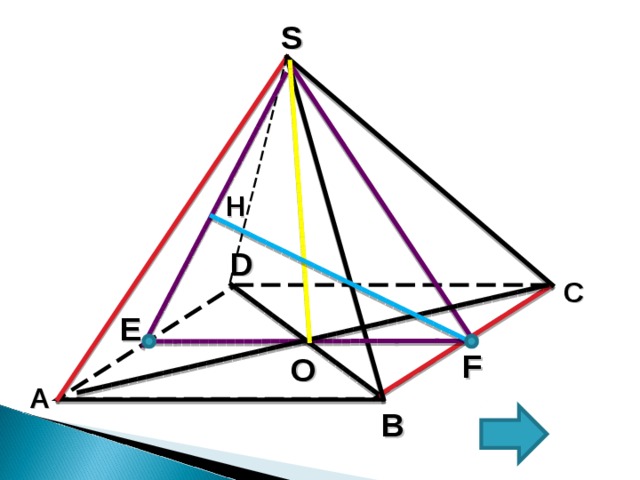
4. Пусть E и F соответственно середины ребер AD и BC .
Тогда искомым перпендикуляром будет высота FH ∆ SEF .
5. В ∆ SEF : EF =АВ=1; SE=SF -высоты равнобедренных ∆ SAD и ∆ SBC соответственно, = SE=SF =√3/2
SO – высота четырехугольной пирамиды из прямоугольного ∆ SOF по теореме Пифагора: SO =√2/2.
6. Найдем FH используя способ площадей.
Площадь ∆ SEF найдем двумя способами.
7. S ∆ SEF=(1/2)∙EF∙SO
S ∆ SEF=(1/2)∙1∙ ( √ 2/2)=√2/4
8. S ∆ SEF=(1/2)∙SE∙HF ,
= HF=(√2/4)/((1/2)∙√3/2)=(√2/4)/(√3/4)=
= √2/√3=√6/3 .
Ответ: √6/3
S
H
D
C
E
O
F
А
B
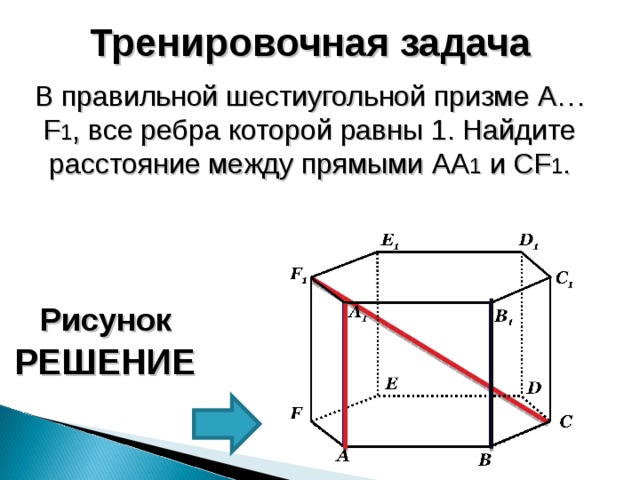
Тренировочная задача
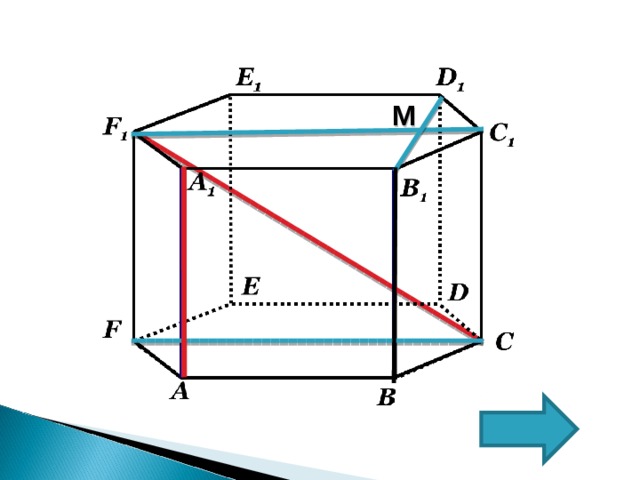
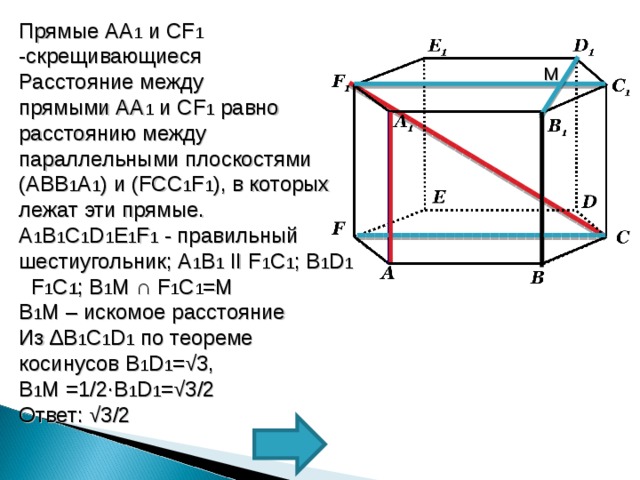
В правильной шестиугольной призме A…F 1 , все ребра которой равны 1. Найдите расстояние между прямыми AA 1 и CF 1 .
Рисунок
РЕШЕНИЕ
M
Прямые АА 1 и СF 1 -скрещивающиеся
Расстояние между
прямыми АА 1 и СF 1 равно
расстоянию между
параллельными плоскостями (АВВ 1 А 1 ) и (FCC 1 F 1 ), в которых
лежат эти прямые.
A 1 B 1 C 1 D 1 E 1 F 1 — правильный шестиугольник; A 1 B 1 II F 1 C 1 ; B 1 D 1 F 1 C 1 ; B 1 M ∩ F 1 C 1 =M
B 1 M – искомое расстояние
Из ∆ B 1 C 1 D 1 по теореме косинусов B 1 D 1 =√3,
B 1 M =1/2∙B 1 D 1 =√3/2
Ответ: √3/2
M




![Rendered by QuickLaTeX.com [ begin{cases} X^2+Y^2+Z^2 = R^2 \ (X-6)^2+Y^2+Z^2 = R^2 \ X^2+Y^2+(Z-4)^2 = R^2 \ (X-3)^2+(Y-3sqrt{3})^2+Z^2 = R^2 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-cc1799655065b3d0f89be57c057d31e3_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} Y^2 = R^2-13 \ (Y-3sqrt{3})^2 = R^2-4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8644bbd0eebf2ed67aab0bbdcc379a40_l3.png)







![Двугранный угол , образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Величина двугранного угла принадлежит промежутку (0°; 180°). Величина угла между пересекающимися плоскостями принадлежит промежутку (0°; 90°]. Угол между двумя параллельными плоскостями равен 0° .](https://fsd.intolimp.org/html/2017/09/18/i_59bfd35d14a4c/img_phpRVR3Z4_S2_22.jpg)