В этом разделе представлен тематический классификатор задачной базы. Вы можете прорешать все задания по интересующим вас темам. Зарегистрированные пользователи получат информацию о количестве заданий, которые они решали, и о том, сколько из них было решено верно. Цветовая маркировка: если правильно решено меньше 40% заданий, то цвет результата красный, от 40% до 80% — желтый, больше 80% заданий — зеленый. Если в оба столбца таблицы выделены зеленым, уровень вашей готовности можно считать достаточно высоким. В столбцах первое число — количество различных уникальных заданий (прототипов), второе число — общее количество заданий, включая задания (клоны), отличающиеся от прототипов только числовыми данными.
| Тема | Кол-во заданий в базе |
Кол-во решенных заданий |
Из них решено правильно |
Проверить себя |
|---|
ГВЭ 2022 11 класс математика
Демонстрационный вариант ГВЭ-11 (10.02.2021) [новая версия]
Демонстрационный вариант ГВЭ-11 письменная форма
Демонстрационный вариант ГВЭ-11 устная форма
Тренировочные варианты ГВЭ СтатГрад
Задание №1
Задание №2
Задание №3
Задание №4
Задание №5
Задание №6
Задание №7
Задание №8
Задание №9
Задание №10
Задание №11
Задание №12
Задание №13
Задание №14
ГВЭ 2023 г. Математика 11 класс демоверсия с ответами. ГВЭ-11 2023 по математике 11 класс ФИПИ Официальные демоверсии государственного выпускного экзамена.
Примеры некоторых заданий из варианта
Математика (письменная форма) ГВЭ-11 2023 г.
spec_MA_pism_gve-11_2023
скачать
Математика (устная форма) ГВЭ-11 2023 г.
spec_MA_ustn_gve-11_2023
скачать
Смотрите также:
ГВЭ 2022 г. Математика 11 класс демоверсия с ответами
ГВЭ
Государственный выпускной экзамен
ГВЭ-11
Официальные демоверсии государственного выпускного экзамена
ГВЭ-9
Официальные демоверсии основного государственного экзамена
Тренировочные сборники для обучающихся с ОВЗ (ГИА-11)
Тренировочные сборники для подготовки к ГИА обучающихся с ОВЗ
Тренировочные сборники для обучающихся с ОВЗ (ГИА-11 для незрячих и слабовидящих)
Тренировочные сборники для подготовки к ГИА обучающихся с ОВЗ
Тренировочные сборники для обучающихся с ОВЗ (ГИА-9)
Тренировочные сборники для подготовки к ГИА-9 обучающихся с ОВЗ
=ГВЭ по математике. 11 класс. Вариант 1
1) Для ремонта подоконников в школе используется шпатлёвка. Сколько банок шпатлёвки необходимо закупить, если одной банки хватает на три подоконника, а всего в школе 49 подоконников требующих ремонта?
2) Розы продаются по 150 рублей за штуку. Какое наибольшее количество роз можно купить на 1000 рублей во время распродажи, когда предоставляется скидка 10%?
3) Найдите корень уравнения:
,4−2x=−x+5.
4) В соревнованиях по метанию копья принимает участие 7 спортсменов из России, 5 из Германии, 4 из Польши и 9 из Австралии. Порядок выступления определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, будет представлять Россию.
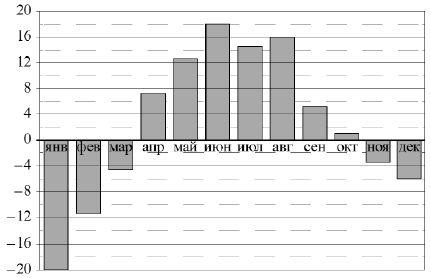
5) На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Череповце в течение 2001 года. Определите наименьшую среднемесячную температуру во второй половине этого года?
6)
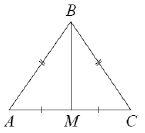
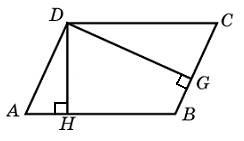
7) В треугольнике АВС известно, что АВ = ВС = 17, АС = 16. Найдите длину медианы ВМ.

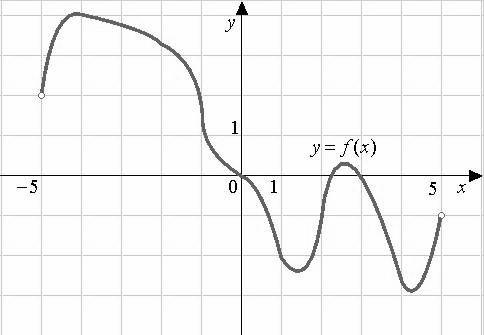
9
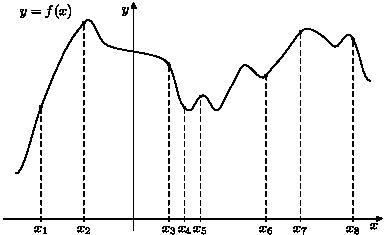
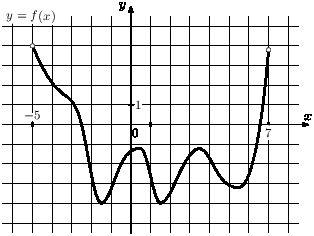
) На рисунке показан график функции y=f(x). Определите число экстремумов этой функции на промежутке (−5;5).
10) Весной баржа идёт по течению реки в 5 раз быстрее, чем против течения. Летом течение становится на 1 км/ч медленнее. Поэтому летом баржа идёт по течению в 3 раза быстрее, чем против течения. Найдите скорость течения весной (в км/ч).
11) а) Решите уравнение: cos(x−5π/2)=4sin ^3x. б) Укажите все его корни, принадлежащие промежутку[3π/2;5π/2].
12) В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка K — середина AC, точка M — середина AA1. Найдите угол BKM.
ГВЭ по математике. 11 класс. Вариант 2
1) Школа организует экскурсию для учащихся и сотрудников. Сколько экскурсионных автобусов, вместимостью 25 мест каждый, необходимо заказать, если желание поехать на экскурсию изъявили 128 учащихся и 14 сотрудников школы?
2) Налог на доходы в России составляет 13%. Определите зарплату врача до уплаты налога на доходы, если после его уплаты он получает на руки 21750 рублей.
3) Найдите корень уравнения: 6−4x=−9x−5.
4) Вероятность того, что на экзамене по физике студент решит правильно 4 или более задач равна 0,15, а вероятность того, что он решит правильно 3 или более задач равна 0,36. Найдите вероятность того, что студент решит правильно ровно 3 задачи.
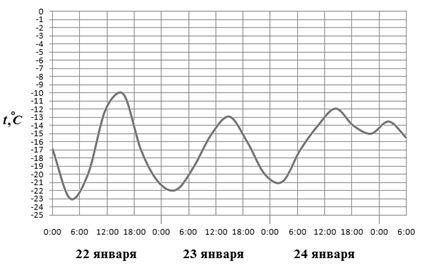
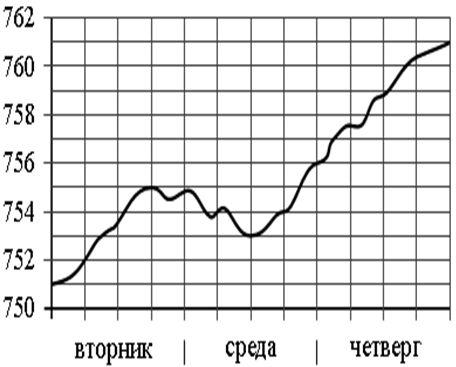
5) На графике показаны колебания температуры воздуха (в градусах Цельсия) в течение трёх суток. Определите, на сколько градусов Цельсия наибольшая температура 23 января превосходила наименьшую температуру в этот же день.
6)
7) Стороны параллелограмма равны 45 и 54. Высота, проведенная к большей стороне, равна 20. Найдите высоту, проведенную к меньшей стороне параллелограмма.

9) На рисунке показан график дифференцируемой функции y=f(x) и отмечены восемь точек на оси абсцисс: x1,x2,…,x8. Среди этих точек найдите все точки, в которых производная функции y=f(x) отрицательна. В ответ запишите количество найденных точек.
10) Маша и Медведь отправляются из одного и того же места на прогулку к пруду, расположенному в 5 км от места отправления. Маша бежит со скоростью 12,8 км/ч, а Медведь следует за ней со скоростью 7,2 км/ч. Добежав до пруда, Маша сразу же разворачивается и с той же скоростью бежит обратно. На каком расстоянии от пруда она встретит Медведя?
11) а) Решите уравнение: cos2x+1=sin(π/2−x). б) Укажите все его корни, принадлежащие промежутку [5π/2;4π].
12) В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BCA1.
ГВЭ по математике. 11 класс. Вариант 3
1) В среду в школьной столовой пообедали 8 сотрудников школы и 154 учащихся. Определите выручку столовой, если обед для сотрудника стоит 50 рублей, а учащиеся оплачивают половину указанной стоимости обеда.
2) С зарплаты сторожа, составляющей 15000 рублей, удерживается налог на доходы 13%. Сколько рублей получает сторож на руки после уплаты налога?
3) Найдите корень уравнения: 9x–2(–5+7x)=−8x−59x–2(–5+7x)=−8x−5.
4) Вероятность того, что сданные пациентом анализы позволят врачу сделать вывод о состоянии его здоровья, равна 0,925. Найдите вероятность того, что пациенту придётся сдавать анализы повторно.
5) На графике показаны колебания атмосферного давления (в мм ртутного столба) в течение трёх суток. Определите наименьшее значение атмосферного давления за весь данный период наблюдения. Ответ дать в мм ртутного столба.
6)
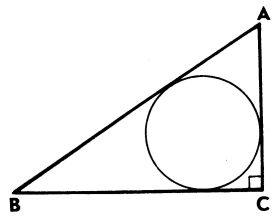
7) В треугольнике АВС угол С прямой, АС = 6, ВС = 8. Найдите радиус вписанной окружности.

9) На рисунке показан график дифференцируемой функции y=f(x)y=f(x). Определите число целых точек из промежутка (−5;7)(−5;7), в которых производная этой функции положительна.
10) Из пункта А в пункт В отправился велосипедист, а через 1 час после этого следом за ним со скоростью, на 9 км/ч большей, отправился мотоциклист. Расстояние между пунктами равно 40 км. Найдите скорость мотоциклиста, если в пункт В он прибыл одновременно с велосипедистом.
11) а) Решите уравнение: cos(3π2+x)=sin2xcos(3π2+x)=sin2x. б) Укажите все его корни, принадлежащие промежутку [3π2;5π2][3π2;5π2].
12) В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
ГВЭ по математике. 11 класс. Вариант 4
1) В течение года Аня купила 36 листов бумаги для рисования, заплатив за каждый из них 24 рубля. Сколько рублей она бы сэкономила, покупая бумагу не поштучно, а в пачках по 12 листов, если стоимость такой пачки 250 рублей?
2) Аптека предоставляет пенсионерам скидку на медикаменты. Определите величину этой скидки в процентах, если за лекарство стоимостью 150 рублей пенсионер заплатил 144 рубля.
3) Найдите корень уравнения: x2−8=(x−2)2×2−8=(x−2)2.
4) Бочонки лото пронумерованы числами от 1 до 25. Найдите вероятность того, что вытащенный наудачу бочонок будет иметь чётный номер.
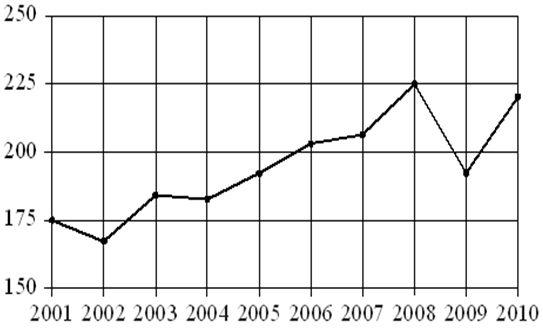
5) График показывает динамику среднегодовой добычи угля в миллионах тонн за период с 2001 по 2010 годы. Определите количество лет из данного интервала наблюдений, в течение которых среднегодовая добыча угля превосходила 200 миллион тонн.
6)
7) В треугольнике АВС известно, что АВ = ВС = 13, медиана ВМ = 12. Найдите длину АС.

9) Материальная точка движется прямолинейно по закону x(t)=6t2+48t+17 где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9с..
10) Бригада асфальтоукладчиков должна уложить 600 кв. метров асфальта. Если они будут укладывать на 50 кв. метров в день больше, чем запланировано, то закончат работу на 2 дня раньше. Сколько кв. метров асфальта в день должна укладывать бригада по плану?
11) а) Решите уравнение: 3cosx⋅5sinx=15cosx . б) Укажите все его корни, принадлежащие промежутку[5π;13π/2].
12) В правильной четырёхугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки A до плоскости SCD.
ГВЭ по математике. 11 класс. Вариант 5
1) Игорь живёт в квартире № 117 шестиэтажного дома, имеющего несколько подъездов. В каждом из них на каждом этаже находится по 4 квартиры. Определите номер подъезда, в котором живёт Игорь.
2) В институте 240 студентов изучает испанский язык, что составляет 15% от числа всех студентов. Сколько студентов обучается в данном институте.
3) Найдите корень уравнения: x2+11=(x−11)2.
4) 30 рыбаков, оказавшихся на отколовшейся льдине, спасает вертолёт, забирая по 6 человек за рейс? Найдите вероятность того, что рыбак Н. полетит вторым рейсом, если порядок, в котором рыбаки садятся в вертолёт, случаен.
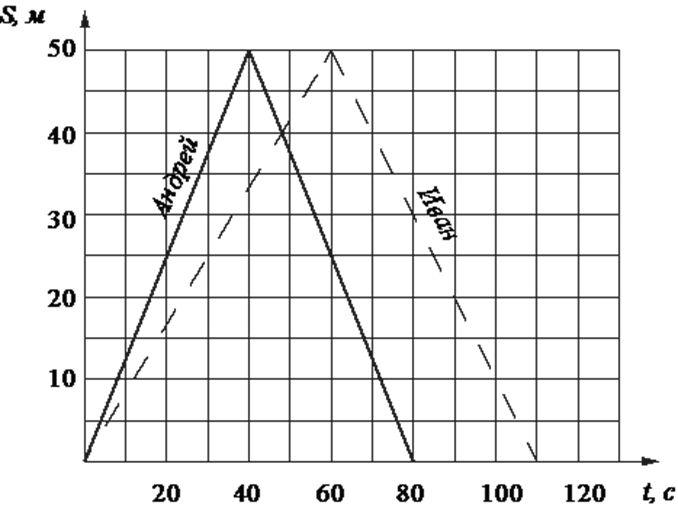
5) Андрей и Иван соревнуются в плавании на дистанции 100 м в пятидесятиметровом бассейне. Определите, сколько времени понадобилось победителю этого соревнования, чтобы преодолеть первую половину дистанции. Ответ дать в секундах.
6) Поставьте в соответствие каждому неравенству множество его решений.
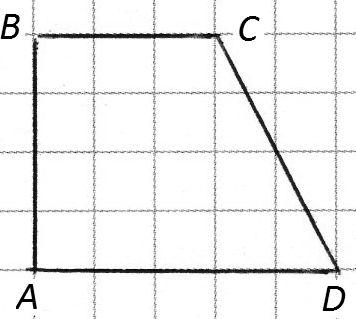
7) В треугольнике ABCABC AC=BC=16AC=BC=16, cosA=0,75cosA=0,75. Найдите ABAB.

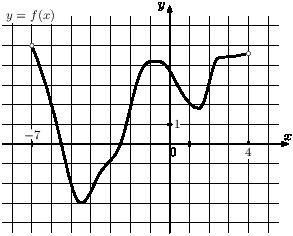
9) На рисунке показан график дифференцируемой функции y=f(x)y=f(x). Определите число целых точек из промежутка (−7;4)(−7;4), в которых производная этой функции отрицательна.
10) Теплоход в 10:00 вышел из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа, теплоход отправился назад и вернулся в пункт А в 17:00. Определите собственную скорость теплохода (в км/ч), если скорость течения реки 8 км/ч.
11) а) Решите уравнение: 2cos2x=√3sin(x+3π2)2cos2x=3sin(x+3π2) . б) Укажите все его корни, принадлежащие промежутку [π;5π2][π;5π2].
12) В правильной четырёхугольной пирамиде SABCDSABCD, все ребра которой равны 1, найдите расстояние между прямыми SB и AC.
№1 4sin^3 x = cos (x — 5п2)
У косинуса знак не выносится, значит, просто меняем.
4sin^3 x = cos (5п2 — x)
Отбрасываем целую часть.
4sin^3 x = cos (п2 — x)
4sin^3 x = sin x
sinx * (4sin^2 x — 1) = 0
1) sinx = 0
x = пn
Выбираем корни из промежутка:
3п2
3п
3
1.5
n = 2, x = 2п
2) sinx = 12
x = (-1)^n * п6 + пn
3п2
9п
8п
8
43
n = 2, x = п6 + 2п = 13п6
3п2
9п
10п
10
53
n = 2, x = -п6 + 2п = 11п6
3) sinx = -12
x = (-1)^(n+1) * п6 + пn
Те же корни, что и sinx = 12
Ответ: 11п6, 13п6, 2п
№2 Cos2x=1-cos(p/2-x) cos^2x-sin^2x=sin^2x+cos^2x-sinx -2sin^2x+since=0 sinx(-2sinx+1)=0 sinx=o x=pk,k принадлежит z -2sinx+1=0 sinx=1/2 x=(-1)^k p/6+pk, k принадлежит z
№3