Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 4. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно два раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Спрятать решение
Решение.
Количество способов поставить две 1 на пять позиций —
После того, как определили позиции двух 1, на оставшиеся позиции можем поставить любое из трёх чисел, это можно сделать способами.
Итого всего кодов.
Ответ: 270.
Приведём другое решение на языке Python.
from itertools import product
alphabet = ‘1234’
ap=[]
for i in product(alphabet, repeat=5):
if i.count(‘1’) == 2:
ap.append(i)
print(len(ap))
1
Задание 1. Однозначное соотнесение графа и таблицы
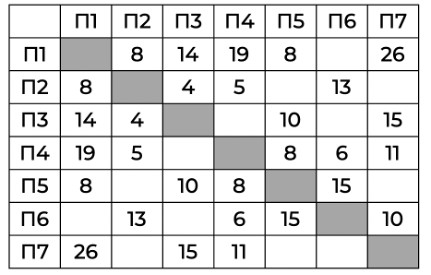
Между населёнными пунктами П1, П2, П3, П4, П5, П6, П7 построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
Определите длину кратчайшего пути между пунктами П1 и П7, проходящего через пункт П6, минуя пункт П2 (при условии, что передвигаться можно только по построенным дорогам).
2
Задание 2. Заполнение таблицы истинности
Логическая функция F задается выражением ((x→w) ≡ (y→z)) / ¬ (w≡y) / ¬ (k→z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F,содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w, k.
| ? | ? | ? | ? | F | |
| 1 | 1 | 1 | |||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 1 |
В ответе напишите буквы x, y, z, w, k в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3
Задание 3. Фильтры и таблицы
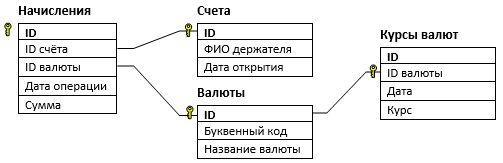
В файле 3-dv.xls приведён фрагмент базы данных «Инвестиционные счета». Таблица «Счета» содержит информацию о владельце счёта и дате его открытия. Таблица «Валюты» содержит информацию о наименованиях валют, которые могут храниться на счетах. Таблица «Курс валют» содержит информацию о курсах валют по отношению к рублю курс валют за период с 24 по 30 декабря 2021 года. Таблица «Начисления» содержит информацию о всех операциях со счетом: код счёта, код валюты, дату операции и сумму начисления (она может быть отрицательной). На рисунке приведена схема указанной базы данных.
Даня и Ваня решили подзаработать, чтобы купить курсы по информатике в лучшей школе 99 баллов. Для этого они хотят найти валюту, которая больше всего прибавила в цене в период с 24 по 30 декабря. Используя информацию из приведённой базы данных, определите буквенное обозначение валюты, которая больше всего прибавила в цене с 24 по 30 декабря. В ответе укажите только 3 заглавные буквы.
4
Задание 4. Минимальная длина кода
По каналу связи передаются сообщения, содержащие девять букв: Х, Д, Б, Р, А, С, Ю, Е, З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Х — 011, Б-000, Р-111, Ю — 010, З — 001, Е — 110. Какое наименьшее количество символов потребуется, чтобы закодировать сообщение ХАРДБАСС?
5
Задание 5. Двоичные алгоритмы
Автомат получает на вход натуральное число N и строит по нему новое число R по следующему алгоритму:
1) Исходное число переводится в двоичную систему счисления
2) Подсчитывается количество значащих 0. Если их кол-во чётно — из числа убирается последняя цифра, иначе справа дописывается ‘1’.
3) Второй шаг повторяется еще один раз
4) Результат переводится в десятичную систему счисления.
Укажите сколько получится различных R, которые можно получить при исходном N на отрезке [200, 300].
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a,b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x+a, y+b). Если числа a, b положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2,-3) переместит Чертёжника в точку (6,-1). Запись
Повтори k раз
Команда1 Команда2 Команда3
конец
означает, что последовательность Команда1 Команда2 Команда3 повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 раз
Сместиться на (4, 6)
Сместиться на (-4, 6)
Сместиться на (-4, -6)
Сместиться на (4, -6)
конец
Найдите площадь полученной фигуры.
7
Задание 7. Кодирование изображений
Danny Golds делает фотоснимки размером 1920×2550 пикселей. На хранение одного кадра отводится 15600 Кбайт. Определите максимальную глубину цвета (в битах на пиксель), которую можно использовать при фотосъёмке.
8
Задание 8. Составление комбинаций
Вероника составляет 13-буквенные слова из букв М, А, Й, К, О, В, выбирая такие, в которых содержится комбинация МАЙКОВА. Сколько слов сможет составить Вероника?
Откройте файл электронной таблицы 9-107.xls, содержащий в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов прямоугольного треугольника, выраженных в градусах. В ответе запишите только число.
С помощью текстового редактора определите, сколько различных чисел встречается в тексте рассказа Валентина Распутина «Уроки французского» (10-d1.docx). Одинаковые числа повторно не считать. В ответе укажите только количество чисел.
11
Задание 11. Пароли с дополнительной информацией
Датчик считывает значения интенсивности поступающего света, которые округляются до одного из 2000 возможных. Каждое считанное значение кодируется одинаковым минимально возможным количеством бит. Известно, что значения считываются сериями по 50 измерений, все серии сохраняются в одном файле. Каждая серия занимает целое количество байт. Если последняя серия содержит меньше 50 значений, она сохраняется в файле с помощью минимально возможного целого количества байт. За время своей работы датчик считал 12312 значений. Какое минимальное целое количество килобайт нужно выделить для хранения файла?
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 223>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 11>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 30 цифр 1, 20 цифр 2 и 10 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
13
Задание 13. Поиск числа путей
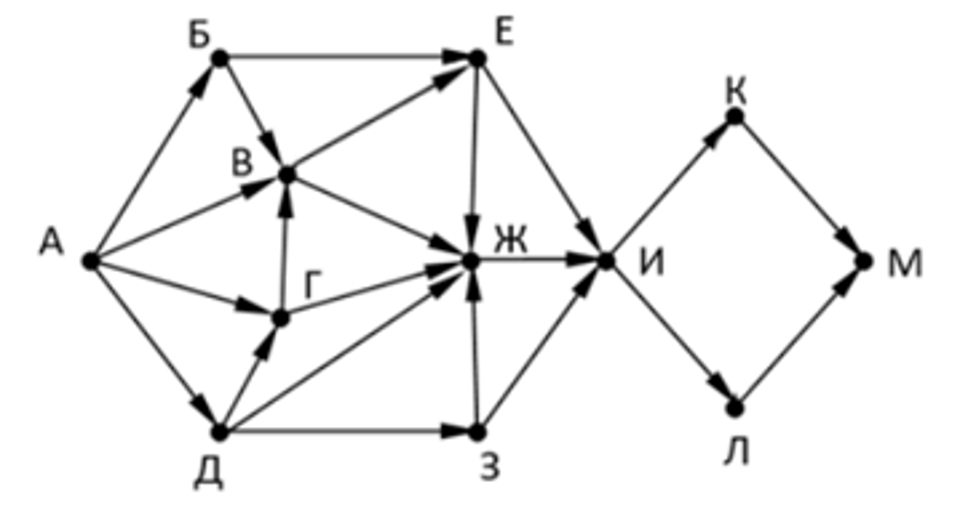
Ваня спешит на пересдачу из общежития (Пункт А) в Иннополис (Пункт М). Чтобы он смог выбрать самый оптимальный маршрут и успеть вовремя, ему нужно знать все возможные варианты добраться до ВУЗа. На рисунке представлена схема дорог, связывающих здания А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из общежития до Иннополиса и не проходящих через военкомат (Пункт В)?
14
Задание 14. Системы счисления (прямое сложение)
Сколько различных цифр в шестнадцатеричной записи числа 2^51 + 2^45 + 2^30 + 4^7 – 2^5
15
Задание 15. Поразрядная коъюнкция
Определите количество натуральных чисел A из интервала [80, 300] таких, что выражение
((X & 55 ≠ 0) (X & 23 ≠ 0)) → (X & A ≠ 0)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?
16
Задание 16. Рекурсивные алгоритмы
Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1
F(n) = F(n–1) + F(n–2), при чётном n > 0
F(n) = 1,5*F(n–1), при нечётном n > 0
Сколько различных цифр встречается в целой части значения функции F(35)?
17
Задание 17. Числовая последовательность
В файле 17-d5.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 1000. Определите сначала количество пар, в которых оба элемента больше, чем сумма всех цифр «3» в шестеричной записи всех чисел в файле, кратных 15, а затем максимальную из сумм таких пар. Под парой подразумевается два идущих подряд элемента последовательности.
18
Задание 18. Двумерное динамическое программирование
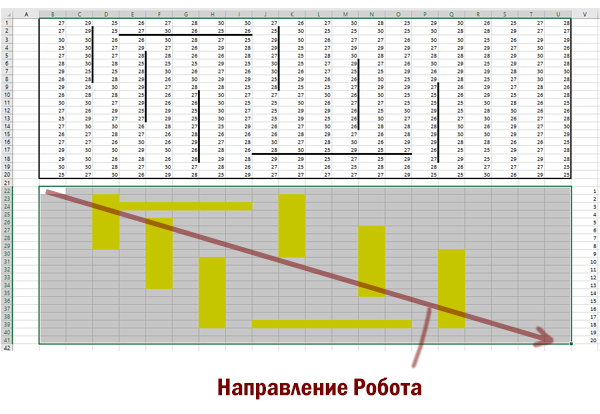
Квадрат разлинован на N×N клеток (1 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трёх команд: вправо, вверх или вправо-вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю, а по команде вправо-вверх – на одну клетку вправо и вверх по диагонали. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записана величина вознаграждения от 1 до 100. Попав в клетку после хода вправо или вверх, Робот получает указанное в ней вознаграждение, а если он попал в клетку после выполнения команды вправо-вверх, вознаграждение удваивается. Это также относится к начальной и конечной клетке маршрута Робота. Определите максимальное и минимальное вознаграждение, которое может получить Робот, пройдя из левой нижней клетки в правую верхнюю. В ответе укажите два числа без пробелов – сначала максимальное вознаграждение, затем минимальное. Исходные данные записаны в файле 18-5.xls в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата.
19
Задание 19. Теория игр (Задания 19)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20
Задание 20. Теория игр (Задания 20)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21
Задание 21. Теория игр (Задания 21)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Сколько существует значений S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22
Задание 22. Параллельные процессы
В файле 22d-3 содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Найдите время завершения процессов 5 из проектов P1 и P2. В ответ укажите их сумму.
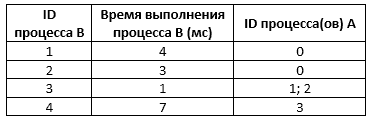
Типовой пример организации данных в файле:
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23
Задание 23. Одномерное динамическое программирование
Исполнитель Шахматный Король преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавь 2
2. Прибавь 3
3. Умножь на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 20 и при этом не содержат двух команд умножения подряд?
24
Задание 24. строковая обработка
Текстовый файл 24-d12.txt содержит заглавные латинские буквы и телефонные номера, всего не более чем 106 символов. Телефонный номер – это последовательность цифр, расположенных между буквами. В некоторой стране Z номер телефона состоит из 11 цифр, начинается на 8 и при этом его вторая слева цифра равна предпоследней. Определите количество телефонных номеров страны Z, содержащихся в файле.
25
Задание 25. Поиск делителей
Найдите наименьшее натуральное число, которое имеет ровно 1024 делителя. В ответе запишите сначала само число и затем его наибольший простой делитель. Подсказка: используйте основную теорему арифметики.
26
Задание 26. Сортировки
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 640 на 480 точек. При попадании очередной частицы на экран в файл записываются координаты чувствительного элемента: номер строки (целое число от 1 до 640) и номер позиции в строке (целое число от 1 до 480). Точка экрана, в которую попала хотя бы одна частица, считается светлой, точка, в которую ни одна частица не попала, – тёмной.
Вам нужно определить наибольшую длину цепочки в одной строке, состоящей только из светлых точек, и строку, в котором она находится. Если таких строк несколько, укажите максимальный из их номеров.
Входные данные представлены в файле 26-73.txt следующим образом. В первой строке входного файла записано целое число N – количество частиц, попавших на экран. В каждой из следующих N строк записаны по два числа, разделённые пробелом: номер строки и номер позиции в строке.
Запишите в ответе два числа: сначала наибольшую длину цепочки из светлых точек, затем – номер строки, в которой находится эта цепочка (если таких строк несколько, запишите максимальный из их номеров).
Пример входного файла:
7
1 2
2 3
3 6
2 4
1 3
2 5
2 4
При таких исходных данных имеется три цепочки светлых точек: в позициях 2 и 3 строки 1, в позициях 4, 5 и 6 строки 2 (это самая длинная цепочка!) и точка в позиции 6 строки 3. Ответ: 3 2.
27
Задание 27. Кратность произведения пары
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов не кратно 10 и 7.
Отличная работа!
Так держать!
Если остались вопросы, напиши своему куратору.
Нужно авторизоваться
Нужно авторизоваться
Введите больше 6 символов
На почту 12345@mail.ru отправлена ссылка для сброса пароля.
Пожалуйста, подтвердите ваш номер телефона
Курс заблокирован
К сожалению, данный курс заблокирован. Необходимо внести доплату
Вывод
средств
Ваше задание
подтверждено!
успешно
Теперь вы можете приступить
к следующему уроку
курса по математике
Перейти к уроку
Подтверждение
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Подтвердить
Ты включаешь автопродление — 25-го числа каждого месяца доступ к купленным курсам будет автоматически продлеваться. Деньги будут списываться с одной из привязанных к учетной записи банковских карт. Управлять автопродлением можно из раздела «Финансы»
Для активации регулярного платежа мы спишем небольшую сумму с карты и сразу её вернем
Вы дествительно хотите отменить автопродление?
Благодарим за покупку!
В ближайшее время курс будет доступен в разделе Моё обучение
Материалы будут доступны за сутки до начала урока
Чат будет доступен после выдачи домашнего задания
Укажите вашу электронную почту
Содержание:
- Решение 8 задания
- Сколько вариантов шифра или кодовых слов
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий
8-е задание: «Измерение количества информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Знание о методах измерения количества информации
До ЕГЭ 2021 года — это было задание № 10 ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Сколько вариантов шифра или кодовых слов
8_1:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.
Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
Ответ: 3125
✍ Показать решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Длина сообщения (L) = 5 символов
- Мощность алфавита (N) = 6 (цифры от 1 до 6).
- Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1).
Найдем количество вариантов для одного случая, а именно: когда единица стоит на первом месте, а остальные 5 цифр размещаем на четыре позиции:
Q = NL
1 5 5 5 5 - 1 * Q = 54 = 625
Найдем количество вариантов двумя разными способами (можно выбрать любой из них):
✎ 1 способ. Найдем количество вариантов методом перебора:
1 5 5 5 5 -1 * Q=54= 625 5 1 5 5 5 -1 * Q=54= 625 5 5 1 5 5 -1 * Q=54= 625 5 5 5 1 5 -1 * Q=54= 625 5 5 5 5 1 -1 * Q=54= 625
✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:
[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]
625 * 5 = 3125
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_2:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).
Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?
Ответ: 810
✍ Показать решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:
Q = NL
Q = 2 * 34 = 162
AB 123 123 123 123 = 162
"2" означает одна из двух букв: А или B, "3" - одна из трех цифр: 2 3 3 3 3 -> Q = 2 * 34 = 162 3 2 3 3 3 -> Q = 2 * 34 = 162 3 3 2 3 3 -> Q = 2 * 34 = 162 3 3 3 2 3 -> Q = 2 * 34 = 162 3 3 3 3 2 -> Q = 2 * 34 = 162
5 * 162 = 810
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_3:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
Ответ: 250
✍ Показать решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:
N = n1 * n2 * n3 * … * nL = nL
Г ? ? ? = 1 * 5 * 5 * 5 = 53 = 125 ? ? ? Г = 5 * 5 * 5 * 1 = 53 = 125
125 + 125 = 250
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_4:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.
Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
Ответ: 80
✍ Показать решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:
Q = NL
N = 3 - 1 = 2 (Y и Z)
(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)
X X ? ? ? -> 12 * Q = 23 = 8
✎1 способ. Перебор всех вариантов:
X X ? ? ? - 12 * Q = 23 = 8 X ? X ? ? - 12 * Q = 23 = 8 X ? ? X ? - 12 * Q = 23 = 8 X ? ? ? X - 12 * Q = 23 = 8 ? X X ? ? - 12 * Q = 23 = 8 ? X ? X ? - 12 * Q = 23 = 8 ? X ? ? X - 12 * Q = 23 = 8 ? ? X X ? - 12 * Q = 23 = 8 ? ? X ? X - 12 * Q = 23 = 8 ? ? ? X X - 12 * Q = 23 = 8
✎ 2 способ. При помощи формулы поиска числа сочетаний:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
Число сочетаний из n элементов по k элементов:
[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]
* Факториал числа: n! = 0 * 1 * 2 * 3 * .. * n
8 * 10 = 80
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_5:
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Типовые задания для тренировки
Ответ: 500
✍ Показать решение:
-
✎ Решение теоретическое:
- Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
- Подсчитаем количество букв на каждой из 5 позиций:
2 5 5 5 2 СН все все все ОЕ
N = n1 * n2 * n3 * … * nL = nL
N = 2 * 5 * 5 * 5 * 2 = 500
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_6:
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
Ответ: 175
✍ Показать решение:
-
✎ Решение теоретическое:
- Количество вариантов различных слов вычислим по формуле:
- n1 — количество вариантов выбора первой буквы и т.п.
- Рассмотрим все варианты расположения буквы Е:
✎ 1 способ:
N = n1 * n2 * n3 * …
где
1. Е ? ? ? или 2. ? Е ? ? или 3. ? ? Е ? или 4. ? ? ? Е Где вопросительный знак означает любую букву из Л, Е, Т, О.
Е ? ? ? = 1 * 4 * 4 * 4 = 64 т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.
? Е ? ? = 3 * 1 * 4 * 4 = 48
? ? Е ? = 3 * 3 * 1 * 4 = 36
? ? ? Е = 3 * 3 * 3 * 1 = 27
64 + 48 + 36 + 27 = 175
Результат: 175
✎ 2 способ:
- Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
- Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:
1. Буква Е используется 4 раза (т.е. на всех позициях): 4 * 4 * 4 * 4 = 256 2. Буква Е не используется совсем (т.е. только 3 буквы): 3 * 3 * 3 * 3 = 81
256 - 81 = 175
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
## var d:='лето'.Cartesian(4).where(w->w.countOf('е')>=1).count.print Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_7:
Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
Ответ: 113
✍ Показать решение:
-
✎ Решение теоретическое:
- Количество возможных вариантов слов вычислим по формуле:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:
N = n1 * n2 * n3 * … * nL = nL
5 * 5 * 5 * 5 = 54 = 625
4 * 4 * 4 * 4 = 44 = 256
р ? ? ? = 1 * 4 * 4 * 4 = 43 ? р ? ? = 4 * 1 * 4 * 4 = 43 ? ? р ? = 4 * 4 * 1 * 4 = 43 ? ? ? р = 4 * 4 * 4 * 1 = 43 Получим 43 * 4 = 256
625 - 256 - 256 = 113
✎ Решение с использованием программирования:
PascalABC.net (традиционный):
|
||
PascalABC.net (LINQ):
|
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_8:
Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Ответ: 624
✍ Показать решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
- 1. Буква А используется 3 раза:
N = n1 * n2 * n3 * … * nL = nL
А А А _ -> 1 * 1 * 1 * 4 = 4 А А _ А -> 1 * 1 * 4 * А = 4 А _ А А -> 1 * 4 * 1 * 1 = 4 _ А А А -> 4 * 1 * 1 * 1 = 4
_ может быть любая из 4 букв: К О М Р. Значит, имеем:4 * 4 = 16 вариантов
А А _ _ -> 1 * 1 * 4 * 4 = 16 А _ А _ -> 1 * 4 * 1 * 4 = 16 А _ _ А -> 1 * 4 * 4 * 1 = 16 _ А А _ -> 4 * 1 * 1 * 4 = 16 _ А _ А -> 4 * 1 * 4 * 1 = 16 _ _ А А -> 4 * 4 * 1 * 1 = 16
_ может быть любая из 4 букв: К О М Р. Значит имеем:16 * 6 = 96 вариантов
А _ _ _ -> 1 * 4 * 4 * 4 = 64 _ А _ _ -> = 64 _ _ А _ -> = 64 _ _ _ А -> = 64
64 * 4 = 256 вариантов
_ _ _ _ -> 44 = 256
16 + 96 + 256 + 256 = 624
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_10:
Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?
Ответ: 29
✍ Показать решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:
N = n1 * n2 * n3 * … * nL = nL
Начинаем с A: A D 4ABCD = 1 * 1 * 4 = 4 Начинаем с B: B A D, B B 2BD, B D 4ABCD = 7 Начинаем с C: C A D, C C 2CD, C D 4ABCD = 7 Начинаем с D: D A 3BCD, D B 2BD, D C 2CD, D D 4ABCD = 11
4 + 7 + 7 + 11 = 29
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_22:
Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.
Сколько слов может составить Лена?
Ответ: 6860
✍ Показать решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
| Python: | ||
| С++: |
Результат: 6860
- Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.
- Подсчитаем общее количество вариантов:
- Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
- Всего в слове 4 гласных, но поскольку две буквы
И, то необходимо считать только 3 гласных. - Всего в слове 5 согласных, однако две из них — буквы
К, поэтому считать следует 4 согласных. - Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:
- Количество слов вычисляется как произведение полученных чисел:
- Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:
- Получили 10 вариантов, и в каждом из них можно составить по 24 слова.
- Таким образом, получим общее количество слов:
- Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.
- Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):
- Посчитаем варианты, которые необходимо исключить. Их будет несколько:
- а) буква ь — на последнем месте:
- б) буква ь — между гласными:
- Посчитаем количество слов, согласно условию задачи:
- Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:
- Рассмотрим два случая построения числа по заданию: 1) начиная с четной цифры и 2) начиная с нечетной цифры. Изобразим схематично числа, указывая сверху возможное количество цифр на разряд:
- Сложим количество вариантов в обеих случаях:
- Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):
- Видим, что каждая последующее число получается путем прибавления в столбик единицы к предыдущему числу. В троичной системе счисления! Т.к. цифр всего три.
- Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в троичной системе счисления.
- Значит, пункту под номером 242 будет соответствовать число 241 в троичной системе счисления.
- Переведем 241 в 3-ю систему делением на 3:
- Перепишем остатки снизу вверх: 22221, им соответствуют буквы УУУУО
- Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):
- Видим, что каждое последующее число получается путем прибавления единицы в столбик к предыдущему (в пятеричной системе счисления! т.к. цифр всего пять).
- Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в пятеричной системе счисления.
- Определим число, которое получится, если мы в начале слова поставим букву К (остальные должны остаться нулями, т.к. числа идут по порядку, а нам необходимо первое, начинающееся с К):
- Полученное число — 2000 — необходимо перевести из пятеричной системы счисления в десятичную, чтобы узнать порядковый номер:
- Поскольку порядковый номер числа всегда на единицу больше самого числа, то имеем 251.
- Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:
- Такой список представляет из себя увеличивающиеся числа 5-й системы счисления.
- Так как букве А соответствует 0, то первое (самое младшее) четырехзначное число без нуля — это 1111.
- Чтобы вычислить под каким номером стоит данное число, переведем его в 10-ю систему и прибавим к результату единицу (так как порядковые номера в списке на единицу больше самих чисел):
- Для решения данного задания необходимо вспомнить две формулы:
- Подставим в первую формулу известное значение — вероятность того, что Василий получил четверку:
- Затем подставим известное по условию значение в формулу вероятности случайного события:
- Поскольку p мы уже нашли, подставим найденное значение и найдем искомое число — количество четверок за четверть:
8_11:
Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.
Например, комбинации ААР или ЕСС не являются допустимыми.
Сколько всего комбинаций можно составить, используя это правило?
Ответ: 66
✍ Показать решение:
-
✎ Решение теоретическое:
1. С гласной:
1.1 2 3 2 = 2 * 3 * 2 = 12 гл с с 1.2 2 3 2 = 2 * 3 * 2 = 12 гл с гл
2. С согласной:
2.1 3 2 2 = 3 * 2 * 2 = 12 с с с 2.2 3 2 3 = 3 * 2 * 3 = 18 с гл с 2.3 3 2 2 = 3 * 2 * 2 = 12 с с гл
12 + 12 + 12 + 18 + 12 = 66
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
Python:
|
||
| С++: |
8_12:
Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.
Ответ: 72
✍ Показать решение:
-
✎ Решение теоретическое:
гл с гл с гл 3 4 2 3 1 оаи крбл оа крб и
3 * 4 * 2 * 3 * 1 = 72
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Результат: 72
8_21:
Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?
Ответ: 3360
Показать решение:
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (программный способ)
📹 Видеорешение на RuTube здесь (программное решение)
8_19:
Петя составляет шестибуквенные слова
перестановкой букв
слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Типовые задания для тренировки
Ответ: 240
✍ Показать решение:
-
✎ Решение теоретическое:
А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. А**А** = 4*3*2*1 = 24 А***А* = 4*3*2*1 А****А = ... *А*А** *А**А* *А***А **А*А* **А**А ***А*А
10 * 24 = 240
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа — множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
8_20:
Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать
ровно 1 раз
, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?
Типовые задания для тренировки
Ответ: 4080
Показать решение:
✎ Решение теоретическое:
7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях ИТОГО: 7! = 5040 слов
6 5 4 3 2 1 Ь = 6! = 720
И Ь Е 4 3 2 1 = 24 варианта Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...): 24 * 5 = 120 Е Ь И 4 3 2 1 = 24 варианта 24 * 5 = 120
5040 - 720 - 120 - 120 = 4080
✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
8_23:
Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?
Ответ: 72
✍ Показать решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, спортивное прогр-е):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 72
Сколько существует n-значных чисел, записанных в m-ной системе счисления
Разбор 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):
Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?
Типовые задания для тренировки
Ответ: 1008
✍ Показать решение:
-
✎ Решение теоретическое:
четные: 0, 2, 4, 6 - итого 4 цифры нечетные: 1, 3, 5, 7 - итого 4 цифры
1) с четной цифры: 3 4 3 3 2 2 1 1 = 3*4*3*3*2*2*1*1 = 432 ч н ч н ч н ч н
Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
2) с нечетной цифры: 4 4 3 3 2 2 1 1 = 4*4*3*3*2*2*1*1 = 576 н ч н ч н ч н ч
Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
432 + 576 = 1008
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Список в алфавитном порядке
8_13:
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…
Запишите слово, которое стоит под номером 242 от начала списка.
Ответ: УУУУО
✍ Показать решение:
-
✎ Решение теоретическое:
1. 00000 2. 00001 3. 00002 4. 00010 ...
остатки 241 | 3 | 1 80 | 3 | 2 26 | 3 | 2 8 | 3 | 2 2 | |
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
Смотрим слова и находим по номеру нужное слово: … (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (теоретический способ)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8 (10) задание. Демоверсия ЕГЭ 2018 информатика:
Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ДДДД 2. ДДДЕ 3. ДДДК 4. ДДДО 5. ДДДР 6. ДДЕД …
Под каким номером в списке идёт первое слово, которое начинается с буквы K?
Ответ: 251
✍ Показать решение:
-
✎ Решение теоретическое:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010 ...
K -> 2 -> 2000
По формуле разложения числа по степеням основания: 20005 = 2 * 53 + 0 * 22 + 0 + 0 = 2 * 125 = 25010
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_15:
Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:
1. ПППП 2. ПППР 3. ПППС 4. ПППТ 5. ППРП ... ...
Ответ: 65
📹 Видео
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_16:
Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:
1. АААА 2. АААВ 3. АААГ 4. АААЕ 5. АААН 6. ААВА …
Под каким номером в списке идёт первое слово, в котором нет буквы А?
Ответ: 157
✍ Показать решение:
-
✎ Решение теоретическое:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010
11115 = 1 * 53 + 1 * 52 + 1 * 51 + 1 * 50 = 156
156 + 1 = 157
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
Вероятность событий
8_17:
За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.
Сколько четверок получил Василий за четверть?
Ответ: 5
✍ Показать решение:
1. Формула Шеннона:
x = log2(1/p)
x - количество информации в сообщении о событии p - вероятность события
2. Формула вероятности случайного события:
p(A) = m/n
m - число случаев, способствующих событию А n - общее число равновозможных случаев
2 = log2(1/p);
=>
1/p = 4;
=>
p = 1/4
p = ?/20
1/4 = ?/20
? = 1/4 * 20 = 5
📹 Видео
📹 Видеорешение на RuTube здесь (теоретическое решение)
Продолжаем решать демоверсию ЕГЭ по информатике 2023.
Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
В этой статье разберём задания 16-21 из демоверсии ЕГЭ по информатике 2023.
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Задание 16
Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?
Решение:
Если мы просто перепечатаем функцию, как мы делали на экзамене в 2022 году, то программа откажится это вычислять. Здесь слишком большая глубина рекурсии.
Тогда посмотрим внимательно на функцию. Оказывается это функция факториала. Это действие означает n! = 1*2*3*…*n.
F(2023) / F(2020) = (2023 * 2022 * 2021 * 2020!) / 2020! = 2023 * 2022 * 2021
Выражение 2020! просто сокращается. В ответе напишем 2023 * 2022 * 2021 = 8266912626.
Ответ: 8266912626
Задание 17
В файле содержится последовательность целых чисел. Элементы
последовательности могут принимать целые значения от –10 000 до 10 000
включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары
не меньше квадрата максимального элемента последовательности,
оканчивающегося на 3. В ответе запишите два числа: сначала количество
найденных пар, затем максимальную из сумм квадратов элементов таких
пар. В данной задаче под парой подразумевается два идущих подряд
элемента последовательности.
Решение:
В начале нужно найти максимальное число последовательности, оканчивающегося на 3.
f=open('17.txt') mx=-10000 for s in f.readlines(): x=int(s) if abs(x)%10==3: mx = max(mx, x) print(mx)
Получается число 9973.
Напишем основную программу:
f=open('17.txt') k=0 mx=0 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if ((abs(n1)%10==3) != (abs(n2)%10==3)) and (n1**2 + n2**2 >= 9973**2): k=k+1 mx = max(mx, n1**2 + n2**2) n1=n2 print(k, mx)
Как решать подобные задачи было рассказано в видеокурсе.
Здесь нужно помнить, что числа отрицательные. Поэтому при нахождении последней цифры, нужно использовать функцию модуля abs.
Так же здесь интересное логическое выражение «в которых только одно число оканчивается на 3». Это операция xor — отрицание равносильности.
Ответ:
Задание 18
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Решение:
Открываем файл в программе Excel.
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
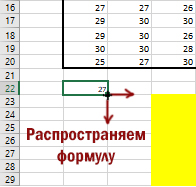
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
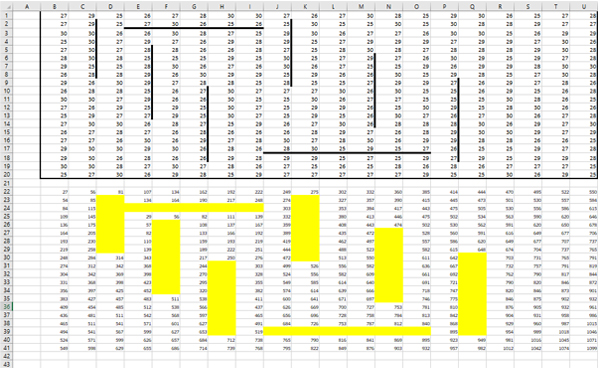
Распространим формулу на всё пространство, не трогая закрашенные клетки.
Получается такая картина:
Для вертикальных подкрашенных полосок, Робот может попасть только сверху! Поэтому пишем формулу для ячейки, к примеру, для D23:
=D22+D2
Распространяем формулу по всему закрашенному столбцу. Аналогично делаем для всех вертикальны подкрашенных полосок.
В ячейки для горизонтально подкрашенных полосок, Робот может попасть только слева! Поэтому пишем формулу, к примеру, для ячейки E24:
=D24+E3
Распространяем формулу по всей закрашенной строчке. Алагоично делаем со всеми горизонтальными полосками.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 1099.
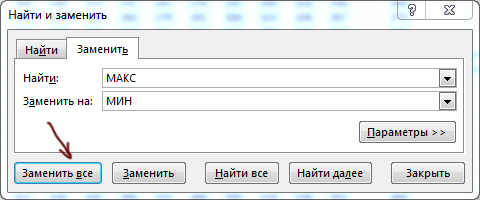
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 1026.
Ответ:
Задание 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит
куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход
игрок может добавить в кучу один камень или увеличить количество камней
в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть
неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится
не менее 129. Победителем считается игрок, сделавший последний ход,
т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может
выиграть при любых ходах противника. Описать стратегию игрока – значит
описать, какой ход он должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника. В описание выигрышной
стратегии не следует включать ходы играющего по этой стратегии игрока,
не являющиеся для него безусловно выигрышными, т.е. не являющиеся
выигрышными независимо от игры противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход,
но при любом ходе Пети Ваня может выиграть своим первым ходом.
Решение:
Решим задачу с помощью шаблона на языке программирования Python. Если хотите ознакомится с аналитическим решением задач на теорию игр, можете посмотреть мои статьи по 19 Заданию, 20 Заданию, 21 Заданию. Но с помощью шаблонов на экзамене решать быстрее и легче. Об этом подходе можете найти в видеокурсе.
Введём параметр p, который будет олицетворять позицию игры (ход).
| Начальная позиция | Ход Пети | Ход Вани | Ход Пети | Ход Вани | Ход Пети | |
| p | 1 | 2 | 3 | 4 | 5 | 6 |
def F(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Заводим функцию F. Т.к. у нас одна куча, то она принимает параметры: x — количество камней в куче, p-позиция игры.
Дальше описываем победу. Если x>=29 и позиция равна 3 (1 Ход Вани), то возвращаем True, что означает победу.
Если, позиция уже равна 3, но камней меньше, чем должно быть для победы, то возвращаем False (проигрыш).
Третье условие. Если кто-то выиграл, но на первых двух условиях мы не вышли из функции, то, значит, выиграл не тот, кто нам нужен, следовательно, возвращаем Fasle.
Если мы не вышли на первых трёх условиях, то, значит, продолжаем прокручивать ходы, рекурсивно запускаем функцию F.
Для нечётных p (это ходы Вани), возвращаем разные ходы через and, т.к. он должен побеждать в любом случае. При этом увеличиваем на 1 значение p.
Для чётных p (это ходы Пети), возвращаем ходы через or.
В конце перебираем все возможные значения для s через цикл for, ищём те значения, которые подходят по условию задачи.
Ответ: 64
Задание 20
Для игры, описанной в задании 19, найдите два наименьших таких значения S, при
которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как
будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение:
Задача точно такая же, как и в 19 задании, только теперь обязательно должен побежать Петя на своём втором ходу (p=4), при любой игре Вани.
Пишем тот же шаблон, немного отредактировав его.
def F(x, p): if x>=129 and p==4: return True if x<129 and p==4: return False if x>=129: return False if p%2==0: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Получается 32 и 63.
Ответ:
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором
одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Решение:
Опять используем прошлый шаблон, но немного модернизируем.
def F(x, p): if x>=129 and (p==3 or p==5): return True if x<129 and p==5: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) def F1(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F1(x+1, p+1) and F1(x*2, p+1) else: return F1(x+1, p+1) or F1(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s) print() for s in range(1, 129): if F1(s, 1): print(s)
Здесь Ваня должен выигрывать либо на первом своём ходе (p=3), либо на втором своём ходе (p=5).
Т.к. Ваня не должен гарантированно выиграть своим первым ходом, то мы создаём ещё одну функцию F1, похожую на основную функцию F, которая вычисляет, когда Ваня именно гарантированно выигрывает на своём первом ходе (p=3). И, затем, мы из тех чисел, которые получились в первой функции F, исключаем числа, которые получились во второй функции F1.
В первой функции получилось 62,64, а во второй 64. Получается ответ 62.
Ответ: 62
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
3 новых тренировочных варианта к ЕГЭ 2023 по информатике 11 класс по новому формату с ответами и видео решением варианта. Данные пробные варианты вы можете также решать онлайн на сайте. Ответы, файлы для заданий опубликованы в самих вариантах.
посмотреть предыдущие варианты
3 тренировочный вариант ЕГЭ 2023 по информатике 11 класс
3вариант-егэ2023-информатика-тренировочный
4 тренировочный вариант ЕГЭ 2023 по информатике 11 класс
4вариант-егэ2023-информатика-тренировочный
5 тренировочный вариант ЕГЭ 2023 по информатике 11 класс
5вариант-егэ2023-информатика-тренировочный
Пробный вариант №3
1.На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги между пунктами Е и Ж. Передвигаться можно только по указанным дорогам.
Ответ: 14
2.Логическая функция F задаётся выражением ((¬x ˄ y) ≡ z) ˄ w. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z,w. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
Ответ: yzwx
3.В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
Ответ: 1509
4.По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 00, Г — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ? Примечание: условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Ответ: 15
5.Автомат получает на вход четырехзначное число. По этому числу строится новое число по следующим правилам. 1. Умножаются первая и вторая, а также третья и четвертая цифры исходного числа. 2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей). Пример. Исходное число: 5431. Произведения: 5 * 4 = 20; 3 * 1 = 3. Результат: 320. Укажите максимальное число, в результате обработки которого, автомат выдаст число 1214.
Ответ: 7262
6.Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Повтори 10 [Вперёд 15 Направо 60]. Сколько существует точек с целочисленными координатами, лежащими на получившемся контуре?
Ответ: 16
7.Музыкальный фрагмент длительностью 2 минуты записали в формате стерео. Размер полученного файла составил 20 Мбайт. После чего музыкальный фрагмент перевели в формат моно, при этом уменьшив частоту дискретизации вдвое и удалив из фрагмента 24 секунды записи. Полученный фрагмент также сохранили в виде файла. Методы сжатия в обоих случаях не применялись. Найдите размер полученного после преобразования файла в МБайт.
Ответ: 4
8.Вася составляет 3-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Ответ: 13
9.Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел. Определите количество строк таблицы, в которых среднее значение элементов меньше среднего значения между максимальным и минимальным значениями. В ответе запишите только число.
Ответ: 2203
10.С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «Кругом», написанное с заглавной буквы, в тексте поэмы А.С.Пушкина «Руслан и Людмила». В ответе укажите только число.
Ответ: 6
11.При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайт
Ответ: 1388
12.Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. заменить (v, w) нашлось (v) Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Ответ: 205
13.На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через Г?
Ответ: 16
14.Значение арифметического выражения 5 · 2163031 + 4 · 363042 — 3 · 63053 — 3064 записали в системе счисления с основанием 6. Определите сумму цифр в записи этого числа.
Ответ: 30417
15.Для какого наибольшего целого неотрицательного числа А выражение (x + y ≤ 22) ∨ (y ≤ x — 6) ∨ (y ≥ A) тождественно истинна (т.е. принимает значение 1) при любых целых положительных х и у?
Ответ: 9
16.Алгоритм вычисления функции F(n) задан следующими соотношениями: F(n) = –n при n < 0 F(n) = 2n + 1 + F(n–3), если n чётно, F(n) = 4n + 2·F(n–4), если n нечётно. Чему равно значение функции F(33)?
Ответ: 11612
17.В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10 000 включительно. Определите пары, среднее арифметическое в которых больше, чем количество чисел в последовательности, абсолютное значение которых меньше 100. В ответе запишите два числа: сначала количество найденных пар, а затем – максимальную сумму элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Ответ: 385 1990
18.Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записано число от 10 до 99. Посетив клетку с нечетным значением, Робот увеличивает счет на 1; иначе на 2. Определите максимальное и минимальное значение счета, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала минимальную сумму, затем максимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Ответ: 23 32
19.Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. Игрокам доступны следующие ходы: · Уменьшить количество камней в три раза, · Убрать из кучи 10 камней Например, из кучи из 25 камней можно получить кучу из 8 или 15 камней. В таком случае результат кратного уменьшения округляется вниз (берется целая часть). Игра завершается в тот момент, когда количество камней в куче становится не более 10. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Известно, что Ваня выиграл своим первым ходом после неудачного хода Пети. При каком максимальном значении S такое возможно?
Ответ: 98
20.Для условия из задачи 19 известно, что Петя имеет выигрышную стратегию. Укажите минимальное и максимальное значения при которых: · Петя не может победить первым ходом · при любом ходе Вани Петя побеждает своим вторым ходом.
Ответ: 43 128
21.Для условия из задачи 19 известно, что Ваня имеет выигрышную стратегию за один или два хода, при этом не имеет выигрышной стратегии в один ход. Сколько существует значений s при которых такая стратегия может быть реализована.
Ответ: 20
22.В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Ответ: 36
23.Исполнитель Простачок преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 2 2. Прибавить предыдущее 3. Прибавить следующее Первая команда увеличивает число на 2, вторая – на предыдущее (например, число 5 будет преобразовано по правилу 5 + 4), третья – на следующее (аналогично, 5 по правилу 5 + 6 = 11) Сколько существует таких программ, которые исходное число 7 преобразуют в число 63, при этом траектория вычислений не содержит число 43?
Ответ: 116
24.Текстовый файл состоит не более чем из 106 символов X, Y, Z. Определите максимальное количество идущих подряд символов, расположенных в алфавитном порядке (возможно с повторением символов). Для выполнения этого задания следует написать программу.
Ответ: 15
25.Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:– символ «?» означает ровно одну произвольную цифру; – символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность. Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 109, найдите все числа, соответствующие маске 12345?7?8, делящиеся на число 23 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 23.
26.В лесополосе осуществляется посадка плодовых деревьев. Причем саженцы высаживают рядами на одинаковом расстоянии. Между соседними саженцами в одном ряду расстояние 10 метров. В каждом ряду сидят разные виды плодовых деревьев. Через какое-то время осуществляется аэросъемка, в результате которой определяется, какие саженцы прижились. Для успешного перекрестного опыления необходимо, чтобы дерево было на расстоянии не более 20 метров от прижившегося дерева того же вида, иначе оно не будет плодоносить. Определите, какое минимальное количество деревьев нужно посадить, чтобы все деревья могли плодоносить. И минимальный номер ряда, в котором необходимо посадить максимальное количество деревьев. Входные данные: В первой строке входного файла 26.txt находится число N — количество занятых мест(натуральное число, не превышающее 10 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 100 000: номер ряда и номер занятого места. Выходные данные: Два целых неотрицательных числа: минимальное количество деревьев, необходимое к посадке в лесополосе, и минимальный номер ряда, где нужно посадить максимальное количество деревьев.
27.На вход программы поступает последовательность из N целых положительных чисел. Рассматриваются все пары различных элементов последовательности. Необходимо определить количество пар чисел, сумма которых кратна 131. Входные данные. Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 10000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 100 000. Программа должна вывести в первой строке одно число: количество пар чисел, сумма которых кратна 131.
Пробный вариант №4
1)На рисунке справа схема дорог между некоторыми объектами изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация объектов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути между пунктами В и Е. Передвигаться можно только по указанным дорогам.
Ответ: 25
2)Логическая функция F задаётся выражением (¬𝑎⋀¬𝑏) ∨ (𝑏 ≡ 𝑐) ∨ 𝑑. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d. В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Ответ: cdba
3)В файле приведён фрагмент базы данных «Фильмы», содержащий информацию о ряде фильмов. К каждому фильму привязан свой ID. Таблица «Фильмы» содержит информацию о названии фильма, продолжительности фильма в секундах, бюджете фильма в $ (долларах) и о сборах с его показа в $ (долларах).
Ответ: 92
4)В сообщении встречается 50 букв А, 30 букв Б, 20 букв В и 5 букв Г. При его передаче использован неравномерный двоичный префиксный код, который позволил получить минимальную длину закодированного сообщения. Какова она в битах?
Ответ: 185
5)На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. Далее эта запись обрабатывается по следующему правилу: а) если число чётное, то к двоичной записи числа слева дописывается 1, а справа 0. Например, если для исходного числа 100 результатом будет являться число 11000; б) если число нечётное, то к двоичной записи числа слева дописывается 11 и справа дописывается 10. Полученная таким образом запись является двоичной записью искомого числа R. Например, при обработке числа 14 алгоритм работает следующим образом. 1. 11102 2. 14 — четное, R2 = 111100 R10 = 60. Сумма цифр — 6. 610 = 1102 Укажите минимальное число R сумма всех цифр которого в десятичной системе счисления больше 17 и которое может являться результатом работы алгоритма. В ответе запишите сумму всех цифр этого числа в двоичной системе счисления.
Ответ: 10011
6)Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Повтори 151 [Вперёд 10 Направо 300 Вперёд 20 Направо 300]. Сколько раз черепаха пройдет через начало координат? Факт положения черепахи в начале координат перед выполнением алгоритма за прохождение не считать.
Ответ: 50
7)Для хранения в информационной системе документы сканируются с разрешением 400 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 2 Мбайт. В целях экономии было решено перейти на разрешение 100 ppi и цветовую систему, содержащую 64 цвета. Средний размер документа, отсканированного с изменёнными параметрами, составляет 96 Кбайт. Определите количество цветов в палитре до оптимизации.
Ответ: 256
8)Определите количество пятизначных чисел, записанных в девятеричной системе счисления, которые не начинаются с нечетных цифр, не оканчиваются цифрами 1 или 8, а также содержат в своей записи не более одной цифры 3.
Ответ: 18944
9)Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел. Определите количество строк таблицы, в которых хотя бы 3 числа больше среднего арифметического всех чисел в строке. В ответе запишите только число.
Ответ: 1035
10)Текст романа Александра Пушкина «Евгений Онегин» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречаются в тексте слова с сочетанием букв «свет», например «светлый», «света». Отдельные слова «свет» и «Свет» учитывать не следует. В ответе запишите только число.
Ответ: 6
11)При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только десятичные цифры и символы из 12-символьного набора: А, В, C, D, Е, F, G, H, K, L, M, N. В базе данных для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя. Определите объём памяти (в байтах), необходимый для хранения данных о 40 пользователях. В ответе запишите только целое число – количество байт.
Ответ: 880
12)Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. заменить (v, w) нашлось (v) Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Ответ: 17
13)На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Ответ: 18
14)Значение выражения 277 – 3 11 + 36 – x записали в троичной системе счисления, при этом сумма цифр в записи оказалась равной 22. При каком минимальном натуральном x это возможно?
Ответ: 6
15)Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 90) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 80
16)Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n < 3; F(n) = 2 × F(n – 1) – F(n – 2), если n > 2 и при этом n чётно; F(n) = F(n − 1) – 2 × F(n – 2) – 3, если n > 2 и при этом n нечётно. Чему равно значение функции F(15)?
Ответ: 6
17)В файле содержится последовательность натуральных чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых остаток от деления хотя бы одного из элементов на 117 равен минимальному элементу последовательности. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности.
Ответ: 175, 173738
18)Исходные данные для Робота записаны в файле в виде электронной таблицы прямоугольной формы. Робот может двигаться только вверх на соседнюю клетку и вправо на соседнюю клетку. Робот может брать монеты только с тех клеток, где количество монет чётно. Если количество монет нечётно, то Робот не берёт в этой клетке ни одной монеты. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Ответ: 974, 306
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом удвоение разрешено выполнять, только если в куче в данный момент нечётное число камней. Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 4 камней (добавил один камень), то следующим ходом Ваня может получить 5 или 6 камней. Получить 8 камней Ваня не может, так как нельзя удваивать кучу с чётным числом камней. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается, когда количество камней в куче становится не менее 26. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 26 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 25 Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
Ответ: 18
20)Для игры, описанной в задании 19, укажите два значения S, при которых Петя не может выиграть за один ход, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом. В ответе запишите найденные значения в порядке возрастания: сначала меньшее, затем большее.
Ответ: 11, 20
21)Для игры, описанной в задании 19, найдите наименьшее значение S, при котором у Пети есть выигрышная стратегия, позволяющая ему выиграть третьим ходом при любой игре Вани, но у Пети нет стратегии, которая позволяла бы ему гарантированно выиграть первым или вторым ходом.
Ответ: 9
22)В файле содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться только последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Ответ: 35
23)Исполнитель Счётчик преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: 1. Прибавить 5 2. Умножить на 5 Первая команда увеличивает число на экране на 5, вторая умножает его на 5. Программа для исполнителя Счётчик — это последовательность команд. Сколько существует программ, для которых при исходном числе 5 результатом является число 280 и при этом траектория вычислений содержит число 30 и не содержит числа 60? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 5 траектория будет состоять из чисел 10, 50, 55.
Ответ: 12
24)Текстовый файл содержит только заглавные буквы латинского алфавита(ABC…Z). Определите максимальное количество идущих подряд символов, среди которых не более двух букв D. Для выполнения этого задания следует написать программу.
Ответ: 373
25)Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: — символ «?» означает ровно одну произвольную цифру; — символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность. Напишите программу, которая ищет среди целых чисел, превышающих 320400, первые пять чисел, которые делятся на все чётные числа, соответствующие маске 1?. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце — соответствующие им частные от деления на максимальное из чисел, соответствующие маске 1?.
26)В магазине сотовой связи представлены смартфоны различной стоимости. Считается, что K самых дешёвых смартфонов относятся к бюджетному сегменту, а M самых дорогих – к премиум сегменту. По заданной информации о цене каждого из смартфонов определите цену самого дешёвого смартфона премиум сегмента, а также целую часть средней цены телефона из бюджетного сегмента. Входные и выходные данные. В первой строке входного файла находятся три числа, записанные через пробел: N – общее количество смартфонов (натуральное число, не превышающее 10 000), K – количество смартфонов в бюджетном сегменте, M – количество смартфонов в премиум сегменте. В следующих N строках находятся стоимости каждого из смартфонов (все числа натуральные, не превышающие 30000), каждое в отдельной строке. Запишите в ответе два числа: сначала цену самого дешёвого смартфона премиум сегмента, а затем целую часть средней цены телефона из бюджетного сегмента.
27)Дана последовательность, состоящая из N целых неотрицательных чисел. Рассматриваются подпоследовательности исходной последовательности, состоящие из K элементов и содержащие в себе хотя бы один нуль. Гарантируется, что K — нечётное. Среди этих подпоследовательностей найти такие, в которых суммы элементов, расположенных по разные стороны от центра, равны. Центральное число в суммы не учитывается. Найти количество подходящих подпоследовательностей. Входные данные. Даны два входных файла (файл A и файл B). В каждом файле на вход подаётся два числа: N и K. Следом N чисел. При этом (2 ≤ N ≤ 5 000 000).
Демоверсия ЕГЭ 2023 по информатике 11 класс ФИПИ
Демоверсия ЕГЭ 2023 по информатике 11 класс ФИПИ вариант с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
В курсе полностью разобраны программные способы решения задач № 2, 5, 8, 12, 14, 15, 17, 22 в Python.
Теория, видеоразборы, задачи для самостоятельного решения.
Изучение Python с нуля для решения задач ЕГЭ.
What you will learn
- Получите все необходимые знания по Python для успешной сдачи КЕГЭ 2023 по информатике
- Научитесь решать № 2, 5, 8, 12, 14, 15, 17, 22 из КЕГЭ 2023
- Изучите условия, циклы, строки, работу с файлами, списки, множества, кортежи, функции и многое другое
- Овладеете базовыми алгоритмами в программировании
About this course
Данный курс является второй ступенью полной подготовки к КЕГЭ 2023 по информатике.
✅ В курсе изучается вся необходимая теория по программированию на языке Python для ЕГЭ по информатике. Особенностью курса является изучение программирования на языке Python именно на задачах КЕГЭ. Курс будет полезен и тем, кто имеет опыт написания программ на Python, и тем, кто совсем не знаком с программированием.
✅ Приведены эффективные способы решения заданий ЕГЭ с помощью написания программы в Python. Разобраны все нюансы и хитрости решения задач ЕГЭ по информатике в Python.
✅ В курсе полностью разобраны программные способы решения задач № 2, 5, 8, 12, 14, 15, 17, 22 на языке программирования Python.
❗ После покупки курса вы можете начать его прохождение в любое время. Доступ к курсу останется у вас навсегда
❗ Некоторые уроки открыты для свободного прохождения, вы можете попробовать учиться с нами бесплатно.
Данный курс является частью курсов:
- Информатика ЕГЭ 2023. Путь к 100 баллам. № 1 — 23
- Информатика ЕГЭ 2023. Путь к 100 баллам. № 1 — 27
Whom this course is for
Для тех, кто сдаёт ЕГЭ по информатике в 2023 году или в ближайшие года.
Для всех желающих, кто интересуется программированием.
Initial requirements
Курс подходит для учеников с любым уровнем начальных знаний.
Meet the Instructors
How you will learn
Курс разбит по темам на модули. Каждый модуль состоит из уроков. А каждый урок из коротких видеоразборов теории и задач, а также задач с автоматической проверкой для закрепления материала.
Course content
Certificate
Stepik certificate
Price
FAQ
Share this course
https://stepik.org/course/100936/promo
- 10.12.2022
Четвертый тестовый вариант по информатике в формате ЕГЭ 2023 года для 11 класса. Данный тест составлен на основе демоверсии ФИПИ ЕГЭ 2023, с учетом кодификатора и спецификации текущего года. Вариант составлен волонтерским проектом ЕГЭ100БАЛЛОВ https://vk.com/ege100ballov
Скачать PDF вариант вы можете по ссылке ниже. В конце документа содержатся ответы к первой части и подробный разбор и решение с критериями проверки для второй части теста.
- Другие тестовые варианты ЕГЭ по информатике
Работа проводилась 10 октября 2022 года.
- Дополнительные файлы к варианту 4
Есть вопросы? Задавайте их ниже в комментариях!
Некоторые задания из варианта №4
Задание 4
Для кодирования некоторой последовательности, состоящей из букв А, К, Л, О, C, Т решили использовать неравномерный двоичный код, для которого выполняется условие Фано. Для букв А и К использовали соответственно кодовые слова 10, 111. Найдите кодовую последовательность наименьшей длины для кодирования слова КОЛОКОЛ и запишите полученный результат в восьмеричном коде. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Задание 7
Изображение размером 1200х1600 пикселей кодируется с использованием палитры из 2000 цветов. После кодирования пикселей изображение сжимается. Сжатый размер закодированного фрагмента меньше исходного на 21%. К сжатому фрагменту дописывается информация о заголовке и дополнительная информация, которая суммарно занимает 20 Кбайт. Какое минимальное количество Мбайт памяти зарезервировать для хранения полученного файла?
Задание 8
Даша составляет слова из букв слова АТТЕСТАТ. Код должен состоять из 8 букв, и каждая буква в нём должна встречаться столько же раз, сколько в заданном слове. Кроме того, в коде должны стоять рядом две гласные или две согласные буквы. Сколько различных слов может составить Даша?
Задание 11
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 294 символов и содержащий только десятичные цифры и символы из 4550-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 131072 идентификаторов. В ответе запишите только целое число – количество Кбайт.
Задание 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 12) → ¬ДЕЛ(x, 90)) ∨ (x + 2A ≥ 512) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.