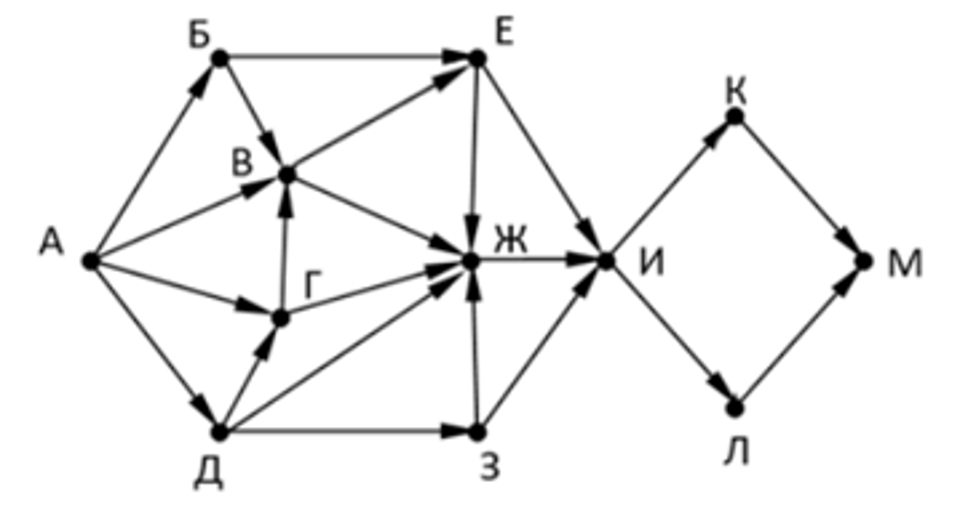
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих через город Ж, но не проходящих через город К?
Решение.
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом если путь должен не проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город наоборот обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
А = 1
Б = А = 1
Д = А = 1
Г = А + Д = 1 + 1 = 2
В = А + Б + Г = 1 + 1 + 2 = 4
Е = Б + В = 1 + 4 = 5
З = В + Г + Д = 4 + 2 + 1 = 7
Ж = В + Е + З = 4 + 5 + 7 = 16
И = Ж = 16
К = И = 16
Л = И = 16
Таким образом, путей, проходящих через город Ж, но не проходящих через город К: М = Л = 16.
Ответ: 16.
1
Задание 1. Однозначное соотнесение графа и таблицы
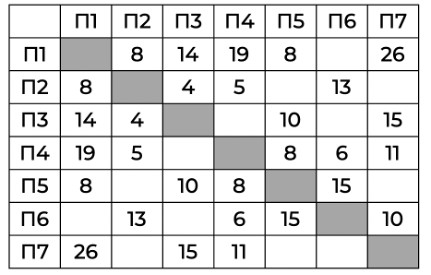
Между населёнными пунктами П1, П2, П3, П4, П5, П6, П7 построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
Определите длину кратчайшего пути между пунктами П1 и П7, проходящего через пункт П6, минуя пункт П2 (при условии, что передвигаться можно только по построенным дорогам).
2
Задание 2. Заполнение таблицы истинности
Логическая функция F задается выражением ((x→w) ≡ (y→z)) / ¬ (w≡y) / ¬ (k→z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F,содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w, k.
| ? | ? | ? | ? | F | |
| 1 | 1 | 1 | |||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 1 |
В ответе напишите буквы x, y, z, w, k в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3
Задание 3. Фильтры и таблицы
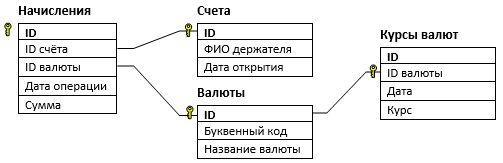
В файле 3-dv.xls приведён фрагмент базы данных «Инвестиционные счета». Таблица «Счета» содержит информацию о владельце счёта и дате его открытия. Таблица «Валюты» содержит информацию о наименованиях валют, которые могут храниться на счетах. Таблица «Курс валют» содержит информацию о курсах валют по отношению к рублю курс валют за период с 24 по 30 декабря 2021 года. Таблица «Начисления» содержит информацию о всех операциях со счетом: код счёта, код валюты, дату операции и сумму начисления (она может быть отрицательной). На рисунке приведена схема указанной базы данных.
Даня и Ваня решили подзаработать, чтобы купить курсы по информатике в лучшей школе 99 баллов. Для этого они хотят найти валюту, которая больше всего прибавила в цене в период с 24 по 30 декабря. Используя информацию из приведённой базы данных, определите буквенное обозначение валюты, которая больше всего прибавила в цене с 24 по 30 декабря. В ответе укажите только 3 заглавные буквы.
4
Задание 4. Минимальная длина кода
По каналу связи передаются сообщения, содержащие девять букв: Х, Д, Б, Р, А, С, Ю, Е, З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Х — 011, Б-000, Р-111, Ю — 010, З — 001, Е — 110. Какое наименьшее количество символов потребуется, чтобы закодировать сообщение ХАРДБАСС?
5
Задание 5. Двоичные алгоритмы
Автомат получает на вход натуральное число N и строит по нему новое число R по следующему алгоритму:
1) Исходное число переводится в двоичную систему счисления
2) Подсчитывается количество значащих 0. Если их кол-во чётно — из числа убирается последняя цифра, иначе справа дописывается ‘1’.
3) Второй шаг повторяется еще один раз
4) Результат переводится в десятичную систему счисления.
Укажите сколько получится различных R, которые можно получить при исходном N на отрезке [200, 300].
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a,b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x+a, y+b). Если числа a, b положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2,-3) переместит Чертёжника в точку (6,-1). Запись
Повтори k раз
Команда1 Команда2 Команда3
конец
означает, что последовательность Команда1 Команда2 Команда3 повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 раз
Сместиться на (4, 6)
Сместиться на (-4, 6)
Сместиться на (-4, -6)
Сместиться на (4, -6)
конец
Найдите площадь полученной фигуры.
7
Задание 7. Кодирование изображений
Danny Golds делает фотоснимки размером 1920×2550 пикселей. На хранение одного кадра отводится 15600 Кбайт. Определите максимальную глубину цвета (в битах на пиксель), которую можно использовать при фотосъёмке.
8
Задание 8. Составление комбинаций
Вероника составляет 13-буквенные слова из букв М, А, Й, К, О, В, выбирая такие, в которых содержится комбинация МАЙКОВА. Сколько слов сможет составить Вероника?
Откройте файл электронной таблицы 9-107.xls, содержащий в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов прямоугольного треугольника, выраженных в градусах. В ответе запишите только число.
С помощью текстового редактора определите, сколько различных чисел встречается в тексте рассказа Валентина Распутина «Уроки французского» (10-d1.docx). Одинаковые числа повторно не считать. В ответе укажите только количество чисел.
11
Задание 11. Пароли с дополнительной информацией
Датчик считывает значения интенсивности поступающего света, которые округляются до одного из 2000 возможных. Каждое считанное значение кодируется одинаковым минимально возможным количеством бит. Известно, что значения считываются сериями по 50 измерений, все серии сохраняются в одном файле. Каждая серия занимает целое количество байт. Если последняя серия содержит меньше 50 значений, она сохраняется в файле с помощью минимально возможного целого количества байт. За время своей работы датчик считал 12312 значений. Какое минимальное целое количество килобайт нужно выделить для хранения файла?
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 223>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 11>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 30 цифр 1, 20 цифр 2 и 10 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
13
Задание 13. Поиск числа путей
Ваня спешит на пересдачу из общежития (Пункт А) в Иннополис (Пункт М). Чтобы он смог выбрать самый оптимальный маршрут и успеть вовремя, ему нужно знать все возможные варианты добраться до ВУЗа. На рисунке представлена схема дорог, связывающих здания А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из общежития до Иннополиса и не проходящих через военкомат (Пункт В)?
14
Задание 14. Системы счисления (прямое сложение)
Сколько различных цифр в шестнадцатеричной записи числа 2^51 + 2^45 + 2^30 + 4^7 – 2^5
15
Задание 15. Поразрядная коъюнкция
Определите количество натуральных чисел A из интервала [80, 300] таких, что выражение
((X & 55 ≠ 0) (X & 23 ≠ 0)) → (X & A ≠ 0)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?
16
Задание 16. Рекурсивные алгоритмы
Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1
F(n) = F(n–1) + F(n–2), при чётном n > 0
F(n) = 1,5*F(n–1), при нечётном n > 0
Сколько различных цифр встречается в целой части значения функции F(35)?
17
Задание 17. Числовая последовательность
В файле 17-d5.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 1000. Определите сначала количество пар, в которых оба элемента больше, чем сумма всех цифр «3» в шестеричной записи всех чисел в файле, кратных 15, а затем максимальную из сумм таких пар. Под парой подразумевается два идущих подряд элемента последовательности.
18
Задание 18. Двумерное динамическое программирование
Квадрат разлинован на N×N клеток (1 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трёх команд: вправо, вверх или вправо-вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю, а по команде вправо-вверх – на одну клетку вправо и вверх по диагонали. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записана величина вознаграждения от 1 до 100. Попав в клетку после хода вправо или вверх, Робот получает указанное в ней вознаграждение, а если он попал в клетку после выполнения команды вправо-вверх, вознаграждение удваивается. Это также относится к начальной и конечной клетке маршрута Робота. Определите максимальное и минимальное вознаграждение, которое может получить Робот, пройдя из левой нижней клетки в правую верхнюю. В ответе укажите два числа без пробелов – сначала максимальное вознаграждение, затем минимальное. Исходные данные записаны в файле 18-5.xls в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата.
19
Задание 19. Теория игр (Задания 19)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20
Задание 20. Теория игр (Задания 20)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21
Задание 21. Теория игр (Задания 21)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Сколько существует значений S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22
Задание 22. Параллельные процессы
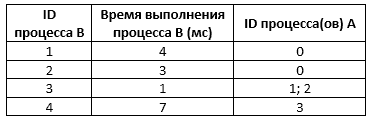
В файле 22d-3 содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Найдите время завершения процессов 5 из проектов P1 и P2. В ответ укажите их сумму.
Типовой пример организации данных в файле:
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23
Задание 23. Одномерное динамическое программирование
Исполнитель Шахматный Король преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавь 2
2. Прибавь 3
3. Умножь на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 20 и при этом не содержат двух команд умножения подряд?
24
Задание 24. строковая обработка
Текстовый файл 24-d12.txt содержит заглавные латинские буквы и телефонные номера, всего не более чем 106 символов. Телефонный номер – это последовательность цифр, расположенных между буквами. В некоторой стране Z номер телефона состоит из 11 цифр, начинается на 8 и при этом его вторая слева цифра равна предпоследней. Определите количество телефонных номеров страны Z, содержащихся в файле.
25
Задание 25. Поиск делителей
Найдите наименьшее натуральное число, которое имеет ровно 1024 делителя. В ответе запишите сначала само число и затем его наибольший простой делитель. Подсказка: используйте основную теорему арифметики.
26
Задание 26. Сортировки
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 640 на 480 точек. При попадании очередной частицы на экран в файл записываются координаты чувствительного элемента: номер строки (целое число от 1 до 640) и номер позиции в строке (целое число от 1 до 480). Точка экрана, в которую попала хотя бы одна частица, считается светлой, точка, в которую ни одна частица не попала, – тёмной.
Вам нужно определить наибольшую длину цепочки в одной строке, состоящей только из светлых точек, и строку, в котором она находится. Если таких строк несколько, укажите максимальный из их номеров.
Входные данные представлены в файле 26-73.txt следующим образом. В первой строке входного файла записано целое число N – количество частиц, попавших на экран. В каждой из следующих N строк записаны по два числа, разделённые пробелом: номер строки и номер позиции в строке.
Запишите в ответе два числа: сначала наибольшую длину цепочки из светлых точек, затем – номер строки, в которой находится эта цепочка (если таких строк несколько, запишите максимальный из их номеров).
Пример входного файла:
7
1 2
2 3
3 6
2 4
1 3
2 5
2 4
При таких исходных данных имеется три цепочки светлых точек: в позициях 2 и 3 строки 1, в позициях 4, 5 и 6 строки 2 (это самая длинная цепочка!) и точка в позиции 6 строки 3. Ответ: 3 2.
27
Задание 27. Кратность произведения пары
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов не кратно 10 и 7.
Отличная работа!
Так держать!
Если остались вопросы, напиши своему куратору.
Нужно авторизоваться
Нужно авторизоваться
Введите больше 6 символов
На почту 12345@mail.ru отправлена ссылка для сброса пароля.
Пожалуйста, подтвердите ваш номер телефона
Курс заблокирован
К сожалению, данный курс заблокирован. Необходимо внести доплату
Вывод
средств
Ваше задание
подтверждено!
успешно
Теперь вы можете приступить
к следующему уроку
курса по математике
Перейти к уроку
Подтверждение
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Подтвердить
Ты включаешь автопродление — 25-го числа каждого месяца доступ к купленным курсам будет автоматически продлеваться. Деньги будут списываться с одной из привязанных к учетной записи банковских карт. Управлять автопродлением можно из раздела «Финансы»
Для активации регулярного платежа мы спишем небольшую сумму с карты и сразу её вернем
Вы дествительно хотите отменить автопродление?
Благодарим за покупку!
В ближайшее время курс будет доступен в разделе Моё обучение
Материалы будут доступны за сутки до начала урока
Чат будет доступен после выдачи домашнего задания
Укажите вашу электронную почту
- 10.03.2023
Шестой тренировочный вариант, составленный на основе демоверсии ЕГЭ 2023 года по информатике от ФИПИ. Вариант включает все задания кодификатора 2023 года и учитывает все изменения, которые произошли в 2023 году (полный список изменений). Вариант содержит правильные ответы и подробные разборы для второй части теста — задания повышенной сложности. Ответы сохранены в конце варианта.
- Другие тренировочные варианты по информатике
Тест может содержать вопросы на различные темы, включая алгоритмы, программирование, базы данных, сети, компьютерную архитектуру и технологии. Вопросы могут быть представлены в различных форматах, таких как выбор одного или нескольких правильных ответов, соответствие, заполнение пропусков, короткий или развернутый ответы. В тесте могут также содержаться задания, требующие написания кода на языке программирования, анализа программного кода, использования различных программных инструментов и знание основных терминов и определений в области информатики.
- Дополнительные файлы для варианта 6
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
ГВЭ 2023 г. Информатика 11 класс демоверсия с ответами. Информатика ГВЭ-11 2023 г. ГВЭ 2023 по информатике 11 класс ФИПИ Официальные демоверсии государственного выпускного экзамена.
Примеры некоторых заданий из варианта
Информатика (письменная форма) ГВЭ-11 2023 г.
spec_INF_pism_gve-11_2023
скачать
Информатика (устная форма) ГВЭ-11 2023 г.
spec_INF_ustn_gve-11_2023
скачать
Смотрите также:
ГВЭ 2022 г. Информатика 11 класс демоверсия с ответами
ЕГЭ информатика 8 задание разбор, теория, как решать.
Перебор слов и комбинаторика, (Б) — 1 балл
Е8.45 в восьмеричной системе счисления требуется ровно 11 цифр, ровно 3 из которых — нечётные
Определите количество чисел, для записи которых в восьмеричной системе счисления требуется ровно 11 цифр, ровно 3 из которых – нечётные, и никакие две нечётные цифры не стоят рядом. Ответ: СтатГрад Вариант ИН22110301 14.02.2023 – задание №8
Читать далее
Е8.44 Определите количество пятизначных чисел, записанных в восьмеричной
Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. Ответ: Демонстрационный вариант ЕГЭ 2023 г. – задание №8
Читать далее
Е8.43 Леонид составляет коды из букв слова ЛЕОНИД.
Леонид составляет коды из букв слова ЛЕОНИД. Код должен состоять из 6 букв, буква Л должна встречаться в нём ровно два раза, буква О – как минимум один раз. Сколько различных кодов может составить Леонид? Ответ: СтатГрад Вариант ИН2110402 30.03.2022 – задание №8
Читать далее
Е8.42 Определите количество семизначных чисел, записанных в семеричной системе счисления
Определите количество семизначных чисел, записанных в семеричной системе счисления, учитывая, что числа не могут начинаться с цифр 3 и 5 и не должны содержать сочетания цифр 22 и 44 одновременно. Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №8 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме
Читать далее
Е8.41 Светлана составляет коды из букв слова РОСОМАХА
Светлана составляет коды из букв слова РОСОМАХА. Код должен состоять из 8 букв, и каждая буква в нём должна встречаться столько же раз, сколько в заданном слове. Кроме того, в коде не должны стоять рядом две гласные и две согласные буквы. Сколько кодов может составить Светлана? Ответ: СтатГрад Вариант ИН2110301 08.02.2022 – задание №8
Читать далее
Е8.40 согласная буква не может стоять в начале слова
Федя составляет 7-буквенные слова из букв П, Л, Ю, С, Ё, Н, О, К, причём согласная буква не может стоять в начале слова, а также рядом с буквой Ё. Буквы в слове могут повторяться. Сколько таких слов может составить Федя? Ответ: «Некрыловские варианты» от Евгения Джобса (И. Женецкий) — Вариант 6
Читать далее
Е8.39 никакие две четные или две нечетные цифры не должны стоять рядом
Аня составляет шестизначные числа в десятичной системе счисления. Цифры в числе не должны повторяться, и никакие две четные или две нечетные цифры не должны стоять рядом. Сколько чисел может составить Аня? Ответ: «Некрыловские варианты» от Евгения Джобса (А. Куканова) — Вариант 5
Читать далее
Е8.38 каждая буква в нём должна встречаться столько же раз, сколько в имени
Светлана составляет коды из букв своего имени. Код должен состоять из 8 букв, и каждая буква в нём должна встречаться столько же раз, сколько в имени Светлана. Кроме того, одинаковые буквы в коде не должны стоять рядом. Сколько кодов может составить Светлана? Ответ: Источник: СтатГрад 17 декабря 2021 года Вариант ИН2110201
Читать далее
Е8.37 Валерия составляет 3-буквенные коды и букв В, А, Л, Е, Р, И, Я, причём буква В
Валерия составляет 3-буквенные коды и букв В, А, Л, Е, Р, И, Я, причём буква В должна входить в код ровно один раз. Все полученные коды Валерия записала в алфавитном порядке и пронумеровала. Начало списка выглядит так: 1. ААВ 2. АВА 3. АВЕ … На каком месте будет записан первый код, не содержащий ни одной …
Читать далее
Е8.36 Настя составляет 6-буквенные коды из букв Н, А, С, Т, Я
Настя составляет 6-буквенные коды из букв Н, А, С, Т, Я. Каждая допустимая гласная буква может входить в код не более одного раза. Сколько кодов может составить Настя? Ответ: СтатГрад Вариант ИН2010501 26.04.2021– задание №8
Читать далее
Подготовка к ЕГЭ. Разбор заданий № 17 «Проверка делимости чисел.» (раздел Программирование).
Автор: Окунева Надежда Евгеньевна
Проверяемые элементы содержания: Умение составить алгоритм обработки числовой последовательности и записать его в виде простой программы (10– 15 строк) на языке программирования
Проверяемые умения или способы действий: Проверяет умение написать простую переборную программу, на языке программирования, содержащую цикл и ветвление. (повышенный уровень, время – 15 мин)
→ скачать материал
Что нужно знать:
Цикл — разновидность управляющей конструкции в высокоуровневых языках программирования, предназначенная для организации многократного исполнения набора инструкций. Последовательность инструкций, предназначенная для многократного исполнения, называется телом цикла. Единичное выполнение тела цикла называется итерацией. Выражение, определяющее, будет в очередной раз выполняться итерация или цикл завершится, называется условием выхода или условием окончания цикла. Переменная, хранящая текущий номер итерации, называется счётчиком цикла.2
Ветвление – (условный оператор) — оператор, конструкция языка программирования, обеспечивающая выполнение определённой команды (набора команд) только при условии истинности некоторого логического выражения, либо выполнение одной из нескольких команд (наборов команд) в зависимости от значения некоторого выражения.
Алгоритм решения:
1. Определить начальные значения входных переменных: k, m, где k – искомое количество чисел из заданного диапазона [a, b], удовлетворяющих заданному условию; k = 0 m – minimax, т.е. если осуществляется поиск минимального значения, то m < a, иначе, при поиске максимального значения m > b.
2. Организовать внешний цикл for, где i изменяется в диапазоне от a до b.
3. Организовать каскад вложенных ветвлений if для осуществления проверки заданных условий:
a. проверка делимости (возможны логические операции or и and);
b. проверка неделимости (применяется логическая операция and);
c. проверка minimaxа.
Примеры заданий:
Вариант № 1
Рассматривается множество целых чисел, принадлежащих числовому отрезку [800; 5900], которые делятся на 17 и не делятся на 2, 3, 5. Найдите количество таких чисел и максимальное из них. В ответе запишите два целых числа: сначала количество, затем максимальное число.
Вариант № 2
Рассматривается множество целых чисел, принадлежащих числовому отрезку [4197; 9182], которые делятся на 5 и не делятся на 6, 10, 13, 16. Найдите количество таких чисел и максимальное из них. В ответе запишите два целых числа: сначала количество, затем максимальное число.
Связанные страницы:
На уроке рассматривается разбор 8 задания ЕГЭ по информатике про измерение количества информации
8-е задание: «Измерение количества информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Знание о методах измерения количества информации
До ЕГЭ 2021 года — это было задание № 10 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«При использовании способа решения со системой счисления с основанием N следует помнить, что слова в списке нумеруются с единицы, поэтому числу 0 будет соответствовать первое слово»
ФГБНУ «Федеральный институт педагогических измерений»
Содержание:
- Объяснение темы
- Измерение количества информации
- Двоичное кодирование сообщений (равновероятностные события)
- Количество различных сообщений в алфавите разной мощности
- Количество сообщений при различном вхождении (встречаемости) букв
- Дополнительные формулы
- Тренировочные задания 8 ЕГЭ по информатике и их решение
- Сколько вариантов шифра или кодовых слов
- Перестановка букв в слове (каждая буква 1 раз)
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий
Объяснение темы
Рассмотрим кратко необходимые для решения 8 задания ЕГЭ понятия и формулы.
Измерение количества информации
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- 1 бит – это количество информации, которое можно передать с помощью одного знака в двоичном коде (0 или 1).
- Алфавит — это набор знаков, используемый в том или ином языке.
- Мощность алфавита — это количество используемых в алфавите знаков.
- Сообщение — это любая последовательность символов какого-либо алфавита.
1 байт (bytе) = 8 бит
1 Кб (килобайт) = 1024 байта
1 Мб (мегабайт) = 1024 Кб
1 Гб (гигабайт) = 1024 Мб
1 Тб (терабайт) = 1024 Гб
1 Пб (петабайт) = 1024 Тб
8 = 23
1024 = 210
Рассмотрим еще несколько определений:
Мощность алфавита
Для вычисления количества информации применяются несколько различных формул в зависимости от ситуации:
Двоичное кодирование сообщений (равновероятностные события)
При вычислении количества информации в сообщении для равновероятностных событий, общее количество которых равно N, используется формула:
N = 2L
* следует иметь в виду, что также приняты следующие обозначения: Q = 2k
Пример 2: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:

Решение:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодовых слов (L = 2).
Количество сообщений длиной L битов:
N = 2L
Т.е. количество сообщений длиной 2 бита, как в примере с нашими буквами, будет равно N = 22 = 4
Ответ: 4
Количество различных сообщений в алфавите разной мощности
Рассмотрим вариант с 5 буквами (мощность алфавита = 5), которые надо разместить в сообщении длиной 2 символа:
Найдем формулу для нахождения количества различных сообщений в алфавите различной мощности:
Если мощность некоторого алфавита составляет N, то количество различных сообщений длиной L знаков:
- N – мощность алфавита
- L – длина сообщения
- Q – количество различных сообщений
Пример: Сколько существует всевозможных трехбуквенных слов в английском языке?
Решение:
В английском алфавите 26 букв. Значит, мощность алфавита = 26. Длина сообщения = 3. Найдем по формуле количество трехбуквенных слов:
Q = 263
или
26
*
26
*
26
= 17576
Ответ: 17576
N = n1 * n2 * … * nL
Количество сообщений при различном вхождении (встречаемости) букв
В таком случае можно использовать формулу для вычисления числа перестановок с повторениями; для двух разных символов она выглядит так:
[ P = frac{na+n*!}{na!n*!} ]
na – количество букв a n* — количество звёздочек или кол-во вариантов
Иногда в заданиях 8 можно использовать формулу комбинаторики для проверки полученных результатов перебора. Число сочетаний из n элементов по k элементов:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
n! = 1 * 2 * 3 * … * n
Пример: Сколько существует всевозможных четырехбуквенных слов в алфавите из 4 букв: А, Б, В, Г, если известно, что буква А встречается ровно два раза?
Решение:
- Длина сообщения = 4. Мощность алфавита = 4. Но мешает условие: буква А встречается ровно два раза.
- В таких заданиях можно использовать способ перебора всевозможных вариантов:
два раза буква А, на остальных местах - одна из трех оставшихся букв: А А 3 3 = 3 * 3 = 32 = 9 А 3 А 3 = 9 А 3 3 А = 9 3 А А 3 = 9 3 А 3 А = 9 3 3 А А = 9
Число сочетаний из n элементов по k элементов:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
[ C{binom{2}{4}}= frac{4!}{2!(4-2)!} = frac{24}{2*2} = 6 ]
* Факториал числа n! = 1 * 2 * 3 *..* n
6 * 9 = 54
Дополнительные формулы
Количество информации и равновероятные события
При определении количества информации для равновероятностных событий могут понадобиться две формулы:
x = log2(1/p)
p(A) = m / n
Количество информации и неравновероятные события
При использовании неравновероятного события, вероятность которого равна p, для вычисления количества информации используется формула:
i = -[log2p]
*квадратные скобки означают ближайшее целое, меньшее или равное значению выражения в скобках
Формула Хартли:
Формула Хартли
Алфавитный подход:
Информационный объем сообщения длиной L:
Алфавитный подход
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Сколько вариантов шифра или кодовых слов
Cartesian(n) — метод расширения последовательности, возвращающий декартову степень множества символов |
Когда применяется: Если требуется полный перебор вариантов букв для каждой позиции (каждая буква может встречаться в кодовом слове любое количество раз) |
||||||
|---|---|---|---|---|---|---|---|
| Пример: Сравним полный перебор букв слова «школа», размещенных на две позиции: |
|||||||
| Pascal | PascalABC.NET | ||||||
|
|
||||||
| Результат: | |||||||
|
[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о] Итого 25 штук (5*5) |
[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о] [к,л] [к,а] [о,ш] [о,к] [о,о] [о,л] [о,а] [л,ш] [л,к] [л,о] [л,л] [л,а] [а,ш] [а,к] [а,о] [а,л] [а,а] |
||||||
Permutations — метод возвращает все перестановки множества элементов, заданного массивом или последовательностью |
Когда применяется: Если требуется перестановка букв в слове. То есть количество каждой буквы в словах сохраняется, и каждая буква встречается только 1 раз |
||||||
| Пример: Сравним перестановку букв слова «мимикрия»: |
|||||||
| Pascal | PascalABC.NET | ||||||
|
|
|
||||||
| Результат: | |||||||
|
[М,И,М,И,К,Р,И,Я] [М,И,М,И,К,Р,Я,И] [М,И,М,И,К,И,Р,Я] [М,И,М,И,К,И,Я,Р] [М,И,М,И,К,Я,Р,И] [М,И,М,И,К,Я,И,Р] [М,И,М,И,Р,К,И,Я] [М,И,М,И,Р,К,Я,И] … |
Используются также следующие запросы и методы LINQ:
Фильтрация последовательностей (Where)
Метод Count([Type -> boolean]) Вычисление скаляра
Метод CountOf(s: Type) — Возвращает количество элементов, равных указанному значению
Метод First() — Возвращает первый элемент последовательности.
Метод Last() — Возвращает последний элемент последовательности.
Метод Pairwise(Self: sequence of T; func: (T,T)->Res) — Превращает последовательность в последовательность пар соседних элементов, применяет func к каждой паре полученных элементов и получает новую последовательность
8_1:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.
Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
✍ Решение:
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Длина сообщения (L) = 5 символов
- Мощность алфавита (N) = 6 (цифры от 1 до 6).
- Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1). Т.е. возьмем вариант, когда 1 стоит на первом месте, а остальные 5 цифр размещаем на 4 позиции:
Q = NL
1 5 5 5 5 - 1 * Q = 54 = 625
✎ 1 способ. Найдем количество вариантов методом перебора:
1 5 5 5 5 -1 * Q=54= 625 5 1 5 5 5 -1 * Q=54= 625 5 5 1 5 5 -1 * Q=54= 625 5 5 5 1 5 -1 * Q=54= 625 5 5 5 5 1 -1 * Q=54= 625
✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:
[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]
625 * 5 = 3125
Результат: 3125
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Детальный теоретический разбор задания 8 ЕГЭ по информатике предлагаем посмотреть в видеоуроке:
📹 YouTube здесьздесь (теоретическое решение)
8_2:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).
Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?
✍ Решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:
Q = NL
Q = 2 * 34 = 162
AB 123 123 123 123 = 162
"2" означает одна из двух букв: А или B, "3" - одна из трех цифр: 2 3 3 3 3 -> Q = 2 * 34 = 162 3 2 3 3 3 -> Q = 2 * 34 = 162 3 3 2 3 3 -> Q = 2 * 34 = 162 3 3 3 2 3 -> Q = 2 * 34 = 162 3 3 3 3 2 -> Q = 2 * 34 = 162
5 * 162 = 810
Результат: 810
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Подробное теоретическое решение данного задания предлагаем посмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_3:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:
N = n1 * n2 * n3 * … * nL = nL
Г ? ? ? = 1 * 5 * 5 * 5 = 53 = 125 ? ? ? Г = 5 * 5 * 5 * 1 = 53 = 125
125 + 125 = 250
Результат: 250
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Видеоразбор данного задания (теоретический способ):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_4:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.
Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:
Q = NL
N = 3 - 1 = 2 (Y и Z)
(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)
X X ? ? ? -> 12 * Q = 23 = 8
✎1 способ. Перебор всех вариантов:
X X ? ? ? - 12 * Q = 23 = 8 X ? X ? ? - 12 * Q = 23 = 8 X ? ? X ? - 12 * Q = 23 = 8 X ? ? ? X - 12 * Q = 23 = 8 ? X X ? ? - 12 * Q = 23 = 8 ? X ? X ? - 12 * Q = 23 = 8 ? X ? ? X - 12 * Q = 23 = 8 ? ? X X ? - 12 * Q = 23 = 8 ? ? X ? X - 12 * Q = 23 = 8 ? ? ? X X - 12 * Q = 23 = 8
✎ 2 способ. При помощи формулы поиска числа сочетаний:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
Число сочетаний из n элементов по k элементов:
[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]
* Факториал числа: n! = 1 * 2 * 3 * .. * n
8 * 10 = 80
* задание достаточно решить одним из способов!
Результат: 80
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Детальный теоретический разбор задания 8 ЕГЭ по информатике теоретическим способом предлагаем посмотреть в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_5:
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
- Подсчитаем количество букв на каждой из 5 позиций:
2 5 5 5 2 СН все все все ОЕ
N = n1 * n2 * n3 * … * nL = nL
N = 2 * 5 * 5 * 5 * 2 = 500
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Результат: 500
Разбор можно также посмотреть на видео (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_6:
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
✍ Решение:
-
✎ Решение теоретическое:
- Количество вариантов различных слов вычислим по формуле:
- n1 — количество вариантов выбора первой буквы и т.п.
- Рассмотрим все варианты расположения буквы Е:
✎ 1 способ:
N = n1 * n2 * n3 * …
где
1. Е ? ? ? или 2. ? Е ? ? или 3. ? ? Е ? или 4. ? ? ? Е Где вопросительный знак означает любую букву из Л, Е, Т, О.
Е ? ? ? = 1 * 4 * 4 * 4 = 64 т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.
? Е ? ? = 3 * 1 * 4 * 4 = 48
? ? Е ? = 3 * 3 * 1 * 4 = 36
? ? ? Е = 3 * 3 * 3 * 1 = 27
64 + 48 + 36 + 27 = 175
Результат: 175
✎ 2 способ:
- Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
- Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:
1. Буква Е используется 4 раза (т.е. на всех позициях): 4 * 4 * 4 * 4 = 256 2. Буква Е не используется совсем (т.е. только 3 буквы): 3 * 3 * 3 * 3 = 81
256 - 81 = 175
Результат: 175
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Теоретическое решение задания 8 смотрите в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_7:
Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
✍ Решение:
-
✎ Решение теоретическое:
- Количество возможных вариантов слов вычислим по формуле:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:
N = n1 * n2 * n3 * … * nL = nL
5 * 5 * 5 * 5 = 54 = 625
4 * 4 * 4 * 4 = 44 = 256
р ? ? ? = 1 * 4 * 4 * 4 = 43 ? р ? ? = 4 * 1 * 4 * 4 = 43 ? ? р ? = 4 * 4 * 1 * 4 = 43 ? ? ? р = 4 * 4 * 4 * 1 = 43 Получим 43 * 4 = 256
625 - 256 - 256 = 113
✎ Решение с использованием программирования:
PascalABC.net (традиционный):
|
||
PascalABC.net (LINQ):
|
||
Python:
|
||
| С++: |
Результат: 113
Теоретическое решение 8 задания предлагаем посмотреть в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_8:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 5-буквенные слова, в которых есть только буквы A, Б, В, и Г, причём буква Г появляется не более одного раза и только на последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква Г появляется не более одного раза и только на последнем месте, значит, она может либо появиться 1 раз на последнем месте, либо не появиться совсем.
- Рассмотрим варианты, когда буква Г встречается 1 раз на последнем месте и встречается 0 раз:
N = n1 * n2 * n3 * … * nL = nL
1 раз: ? ? ? ? Г = 3 * 3 * 3 * 3 * 1 = 34 = 81 0 раз: ? ? ? ? ? = 3 * 3 * 3 * 3 * 3 = 35 = 243
81 + 243 = 324
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 324
8_9:
Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
- 1. Буква А используется 3 раза:
N = n1 * n2 * n3 * … * nL = nL
А А А _ -> 1 * 1 * 1 * 4 = 4 А А _ А -> 1 * 1 * 4 * А = 4 А _ А А -> 1 * 4 * 1 * 1 = 4 _ А А А -> 4 * 1 * 1 * 1 = 4
_ может быть любая из 4 букв: К О М Р. Значит, имеем:4 * 4 = 16 вариантов
А А _ _ -> 1 * 1 * 4 * 4 = 16 А _ А _ -> 1 * 4 * 1 * 4 = 16 А _ _ А -> 1 * 4 * 4 * 1 = 16 _ А А _ -> 4 * 1 * 1 * 4 = 16 _ А _ А -> 4 * 1 * 4 * 1 = 16 _ _ А А -> 4 * 4 * 1 * 1 = 16
_ может быть любая из 4 букв: К О М Р. Значит имеем:16 * 6 = 96 вариантов
А _ _ _ -> 1 * 4 * 4 * 4 = 64 _ А _ _ -> = 64 _ _ А _ -> = 64 _ _ _ А -> = 64
64 * 4 = 256 вариантов
_ _ _ _ -> 44 = 256
16 + 96 + 256 + 256 = 624
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Результат: 624
Теоретическое решение смотрите также на видео:
📹 YouTube здесьздесь (теоретическое решение)
8_10:
Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?
✍ Решение:
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:
N = n1 * n2 * n3 * … * nL = nL
Начинаем с A: A D 4ABCD = 1 * 1 * 4 = 4 Начинаем с B: B A D, B B 2BD, B D 4ABCD = 7 Начинаем с C: C A D, C C 2CD, C D 4ABCD = 7 Начинаем с D: D A 3BCD, D B 2BD, D C 2CD, D D 4ABCD = 11
4 + 7 + 7 + 11 = 29
Результат: 29
Видеоурок демонстрирует подробное теоретическое решение задания:
📹 YouTube здесьздесь (теоретическое решение)
8_22:
Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.
Сколько слов может составить Лена?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
| Python: | ||
| С++: |
Результат: 6860
Использование метода Pairwise()
8_11:
Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.
Например, комбинации ААР или ЕСС не являются допустимыми.
Сколько всего комбинаций можно составить, используя это правило?
✍ Решение:
-
✎ Решение теоретическое:
- Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.
1. С гласной:
1.1 2 3 2 = 2 * 3 * 2 = 12 гл с с 1.2 2 3 2 = 2 * 3 * 2 = 12 гл с гл
2. С согласной:
2.1 3 2 2 = 3 * 2 * 2 = 12 с с с 2.2 3 2 3 = 3 * 2 * 3 = 18 с гл с 2.3 3 2 2 = 3 * 2 * 2 = 12 с с гл
12 + 12 + 12 + 18 + 12 = 66
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
Python:
|
||
| С++: |
Результат: 66
Перестановка букв в слове (каждая буква 1 раз)
8_12:
Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.
✍ Решение:
-
✎ Решение теоретическое:
- Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
- Всего в слове 4 гласных, но поскольку две буквы
И, то необходимо считать только 3 гласных. - Всего в слове 5 согласных, однако две из них — буквы
К, поэтому считать следует 4 согласных. - Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:
гл с гл с гл 3 4 2 3 1 оаи крбл оа крб и
3 * 4 * 2 * 3 * 1 = 72
Результат: 72
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Результат: 72
8_21:
Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?
✍ Решение:
-
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 3360
Подробное решение программным способом смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (программное решение)
8_19:
Петя составляет шестибуквенные слова
перестановкой букв
слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:
А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. А**А** = 4*3*2*1 = 24 А***А* = 4*3*2*1 А****А = ... *А*А** *А**А* *А***А **А*А* **А**А ***А*А
10 * 24 = 240
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа — множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Ответ: 240
8_20:
Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать
ровно 1 раз
, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.
- Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):
7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях ИТОГО: 7! = 5040 слов
6 5 4 3 2 1 Ь = 6! = 720
И Ь Е 4 3 2 1 = 24 варианта Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...): 24 * 5 = 120 Е Ь И 4 3 2 1 = 24 варианта 24 * 5 = 120
5040 - 720 - 120 - 120 = 4080
✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Ответ: 4080
8_23:
Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, спортивное прогр-е):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 72
Сколько существует n-значных чисел, записанных в m-ной системе счисления
8_18: Объяснение 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):
Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:
четные: 0, 2, 4, 6 - итого 4 цифры нечетные: 1, 3, 5, 7 - итого 4 цифры
1) с четной цифры: 3 4 3 3 2 2 1 1 = 3*4*3*3*2*2*1*1 = 432 ч н ч н ч н ч н
Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
2) с нечетной цифры: 4 4 3 3 2 2 1 1 = 4*4*3*3*2*2*1*1 = 576 н ч н ч н ч н ч
Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
432 + 576 = 1008
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 1008
Список в алфавитном порядке
8_13:
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…
Запишите слово, которое стоит под номером 242 от начала списка.
✍ Решение:
-
✎ Решение теоретическое:
- Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):
1. 00000 2. 00001 3. 00002 4. 00010 ...
остатки 241 | 3 | 1 80 | 3 | 2 26 | 3 | 2 8 | 3 | 2 2 | |
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
Смотрим слова и находим по номеру нужное слово: … (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: УУУУО
Подробное решение теоретическим способом смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_14: 8 задание. Демоверсия ЕГЭ 2018 информатика:
Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ДДДД 2. ДДДЕ 3. ДДДК 4. ДДДО 5. ДДДР 6. ДДЕД …
Под каким номером в списке идёт первое слово, которое начинается с буквы K?
✍ Решение:
-
✎ Решение теоретическое:
- Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010 ...
K -> 2 -> 2000
По формуле разложения числа по степеням основания: 20005 = 2 * 53 + 0 * 22 + 0 + 0 = 2 * 125 = 25010
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 251
Подробное решение 8 (10) задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_15:
Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:
1. ПППП 2. ПППР 3. ПППС 4. ПППТ 5. ППРП ... ...
✍ Решение:
Результат: 65
Видеоразбор задания смотрите ниже:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_16:
Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:
1. АААА 2. АААВ 3. АААГ 4. АААЕ 5. АААН 6. ААВА …
Под каким номером в списке идёт первое слово, в котором нет буквы А?
✍ Решение:
- ✎ Решение теоретическое:
- Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010
11115 = 1 * 53 + 1 * 52 + 1 * 51 + 1 * 50 = 156
156 + 1 = 157
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 157
Видеорешение задания (теоретическое):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
Вероятность событий
8_17:
За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.
Сколько четверок получил Василий за четверть?
✍ Решение:
- Для решения данного задания необходимо вспомнить две формулы:
1. Формула Шеннона:
x = log2(1/p)
x - количество информации в сообщении о событии p - вероятность события
2. Формула вероятности случайного события:
p(A) = m/n
m - число случаев, способствующих событию А n - общее число равновозможных случаев
2 = log2(1/p);
=>
1/p = 4;
=>
p = 1/4
p = ?/20
1/4 = ?/20
? = 1/4 * 20 = 5
Результат: 5
Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)