Решу егэ логарифмические функции - Помощь в подготовке к экзаменам и поступлению

Поиск

Всего: 27 1–20 | 21–27

Добавить в вариант

Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.

Найдите наименьшее значение функции

Найдите наибольшее значение функции

Найдите наименьшее значение функции

Найдите точку максимума функции

Найдите наибольшее значение функции

Найдите наименьшее значение функции

Найдите наибольшее значение функции на отрезке

Найдите наименьшее значение функции

Найдите точку максимума функции

Всего: 27 1–20 | 21–27

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Исследование показательных и логарифмических функций

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 11 № 26714

Найдите наименьшее значение функции на отрезке [−2,5; 0].

Аналоги к заданию № 26714: 3847 71037 3849 3851 3853 3855 3857 3859 3861 3863 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 26715

Найдите наибольшее значение функции на отрезке [−4,5; 0].

Аналоги к заданию № 26715: 3865 71087 3867 3869 3871 3873 3875 3877 3879 3881 … Все

Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 19.03.2019. Вариант 2

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 26716

Найдите наименьшее значение функции на отрезке

Аналоги к заданию № 26716: 3885 71137 549375 3887 3889 3891 3893 3895 3897 3899 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 26717

Найдите наибольшее значение функции на отрезке

Аналоги к заданию № 26717: 3905 71187 3907 3909 3911 3913 3915 3917 3919 3921 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 26718

Найдите наименьшее значение функции на отрезке

Аналоги к заданию № 26718: 3925 71217 513682 3927 3929 3931 3933 3935 3937 3939 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №10. Логарифмическая и показательная функции

ЕГЭ Профиль №10. Логарифмическая и показательная функцииadmin2023-01-15T10:24:14+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №10. Логарифмическая и показательная функции

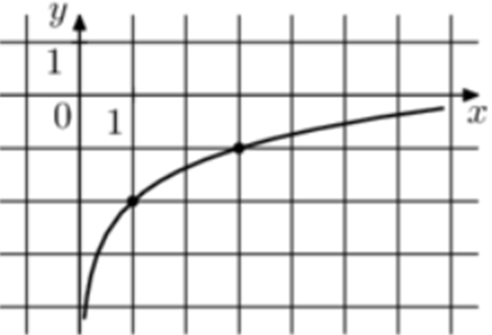
Задача 1. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {27} right).) Ответ ОТВЕТ: 1.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {1; — 2} right)) и (left( {3; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = b + {{log }_a}1}\{ — 1 = b + {{log }_a}3}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{b = — 2,,,,,,,,,,,,,,,,,}\{ — 1 = b + {{log }_a}3}end{array}} right.} right.,,,,,,,, Leftrightarrow ,,,,,,, — 1 = — 2 + {log _a}3,,,,,,, Leftrightarrow ,,,,,,a = 3.) Таким образом: (fleft( x right) = — 2 + {log _3}x) и (fleft( {27} right) = — 2 + {log _3}27 = 1.) Ответ: 1.
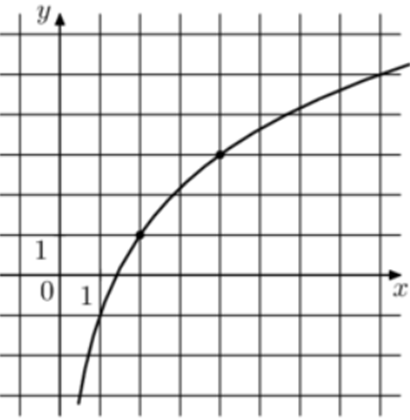
Задача 2. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {16} right).) Ответ ОТВЕТ: 7.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {2;1} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = b + {{log }_a}2}\{3 = b + {{log }_a}4}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = {log _a}2 — {log _a}4,,,,,, Leftrightarrow ,,,,,,,,{log _a}frac{1}{2} = — 2,,,,,,,, Leftrightarrow ,,,,,,,{a^2} = 2,,,,,,, Leftrightarrow ,,,,,,,a = sqrt 2 .) Тогда: (1 = b + {log _{sqrt 2 }}2,,,,,,, Leftrightarrow ,,,,,,1 = b + 2,,,,,,, Leftrightarrow ,,,,,,,,b = — 1.) Следовательно: (fleft( x right) = — 1 + {log _{sqrt 2 }}x) и (fleft( {16} right) = — 1 + {log _{sqrt 2 }}16 = — 1 + 8 = 7.) Ответ: 7.
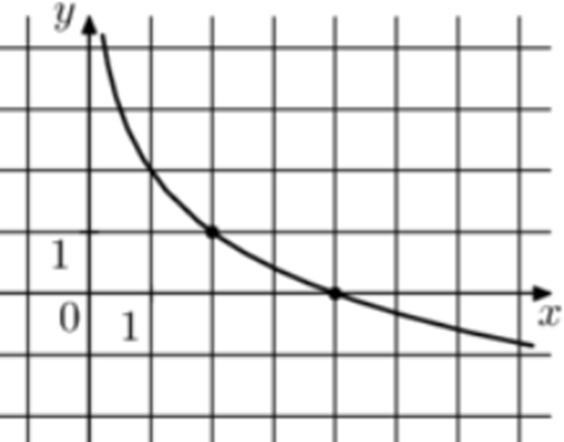
Задача 3. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {128} right).) Ответ ОТВЕТ: — 5.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {2;1} right)) и (left( {4;0} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = b + {{log }_a}2}\{0 = b + {{log }_a}4}end{array}} right.) Вычтем из первого уравнения второе: (1 = {log _a}2 — {log _a}4,,,,,,,, Leftrightarrow ,,,,,,,,{log _a}frac{1}{2} = 1,,,,,,,, Leftrightarrow ,,,,,,,a = frac{1}{2}.) Тогда: (1 = b + {log _{frac{1}{2}}}2,,,,,,, Leftrightarrow ,,,,,,1 = b — 1,,,,,,, Leftrightarrow ,,,,,,,,b = 2.) Следовательно: (fleft( x right) = 2 + {log _{frac{1}{2}}}x) и (fleft( {128} right) = 2 + {log _{frac{1}{2}}}128 = 2 — 7 = — 5.) Ответ: – 5.
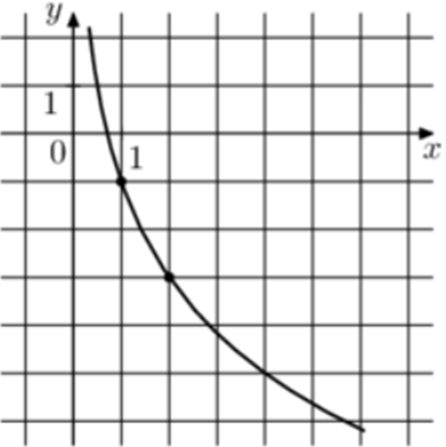
Задача 4. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {0,125} right).) Ответ ОТВЕТ: 5.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {1; — 1} right)) и (left( {2; — 3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = b + {{log }_a}1,}\{ — 3 = b + {{log }_a}2}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{b = — 1,,,,,,,,,,,,,,,,,}\{ — 3 = b + {{log }_a}2}end{array}} right.} right.,,,,,,,, Leftrightarrow ,,,,,,, — 3 = — 1 + {log _a}2,,,,,,, Leftrightarrow ,,,,,,a = frac{1}{{sqrt 2 }}.) Таким образом: (fleft( x right) = — 1 + {log _{_{frac{1}{{sqrt 2 }}}}}x) и (fleft( {frac{1}{8}} right) = — 1 + {log _{_{frac{1}{{sqrt 2 }}}}}frac{1}{8} = — 1 + 6 = 5.) Ответ: 5.
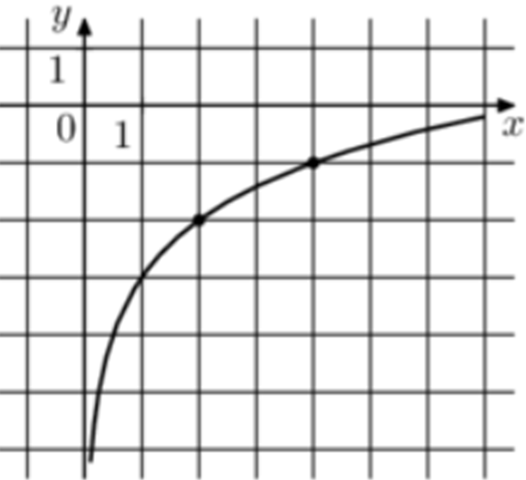
Задача 5. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 3.) Ответ ОТВЕТ: 64.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {1; — 3} right)) и (left( {2; — 2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 3 = b + {{log }_a}1}\{ — 2 = b + {{log }_a}2}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{b = — 3,,,,,,,,,,,,,,,,,}\{ — 2 = b + {{log }_a}2}end{array}} right.} right.,,,,,,,, Leftrightarrow ,,,,,,, — 2 = — 3 + {log _a}2,,,,,,, Leftrightarrow ,,,,,,a = 2.) Таким образом: (fleft( x right) = — 3 + {log _2}x) и ( — 3 + {log _2}x = 3,,,,,,, Leftrightarrow ,,,,,,,,x = 64.) Ответ: 64.
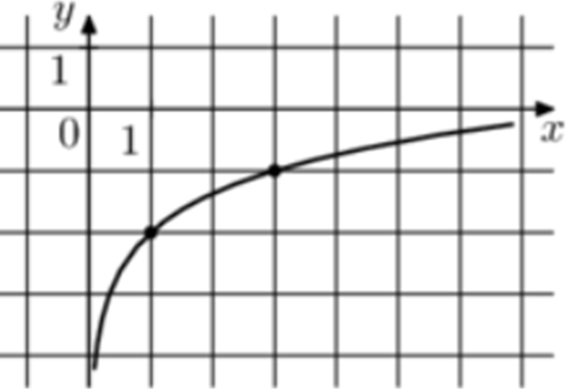
Задача 6. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 2.) Ответ ОТВЕТ: 81.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {1; — 2} right)) и (left( {3; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = b + {{log }_a}1}\{ — 1 = b + {{log }_a}3}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{b = — 2,,,,,,,,,,,,,,,,,}\{ — 1 = b + {{log }_a}3}end{array}} right.} right.,,,,,,,, Leftrightarrow ,,,,,,, — 1 = — 2 + {log _a}3,,,,,,, Leftrightarrow ,,,,,,a = 3.) Таким образом: (fleft( x right) = — 2 + {log _3}x) и ( — 2 + {log _3}x = 2,,,,,,, Leftrightarrow ,,,,,,,,x = 81.) Ответ: 81.
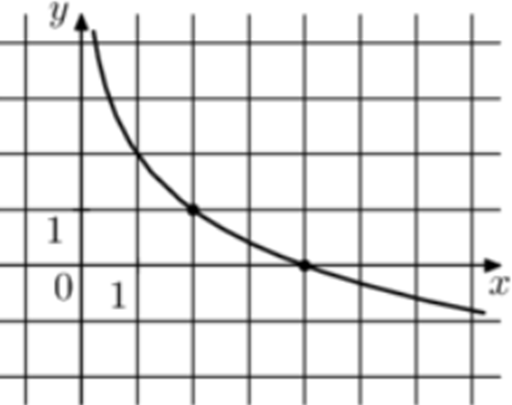
Задача 7. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = — 3.) Ответ ОТВЕТ: 32.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {2;1} right)) и (left( {4;0} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = b + {{log }_a}2}\{0 = b + {{log }_a}4}end{array}} right.) Вычтем из первого уравнения второе: (1 = {log _a}2 — {log _a}4,,,,,,,, Leftrightarrow ,,,,,,,,1 = {log _a}frac{1}{2},,,,,,,, Leftrightarrow ,,,,,,,a = frac{1}{2}.) Тогда: (1 = b + {log _{frac{1}{2}}}2,,,,,,, Leftrightarrow ,,,,,,1 = b — 1,,,,,,, Leftrightarrow ,,,,,,,,b = 2.) Следовательно: (fleft( x right) = 2 + {log _{frac{1}{2}}}x) и (2 + {log _{frac{1}{2}}}x = — 3,,,,,, Leftrightarrow ,,,,,,,,x = 32.) Ответ: 32.
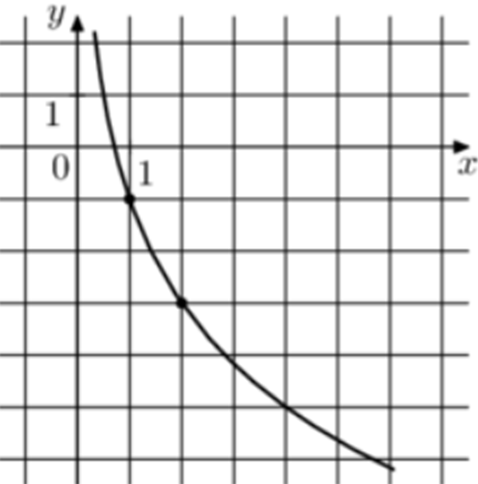
Задача 8. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 3.) Ответ ОТВЕТ: 0,25.
Решение График логарифмический функции (fleft( x right) = b + {log _a}x) проходит через точки (left( {1; — 1} right)) и (left( {2; — 3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = b + {{log }_a}1}\{ — 3 = b + {{log }_a}2}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{b = — 1,,,,,,,,,,,,,,,,,}\{ — 3 = b + {{log }_a}3}end{array}} right.} right.,,,,,,,, Leftrightarrow ,,,,,,, — 3 = — 1 + {log _a}2,,,,,,, Leftrightarrow ,,,,,,a = frac{1}{{sqrt 2 }}.) Таким образом: (fleft( x right) = — 1 + {log _{frac{1}{{sqrt 2 }}}}x) и ( — 1 + {log _{frac{1}{{sqrt 2 }}}}x = 3,,,,,,, Leftrightarrow ,,,,,,,,x = 0,25.) Ответ: 0,25.
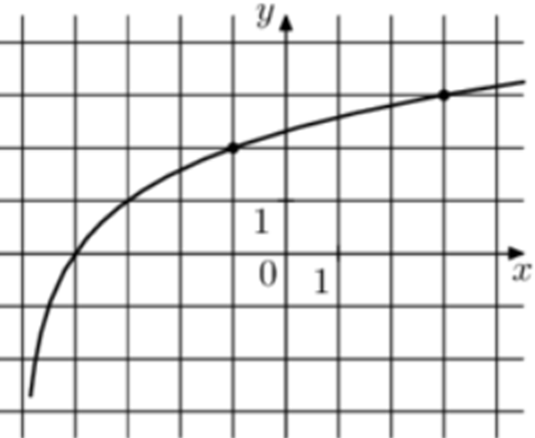
Задача 9. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {27} right).) Ответ ОТВЕТ: 5.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( { — 1;2} right)) и (left( { — 4;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = {{log }_a}left( { — 1 + b} right)}\{0 = {{log }_a}left( { — 4 + b} right)}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{ — 1 + b = {a^2}}\{ — 4 + b = 1}end{array}} right. Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{{a^2} = b — 1}\{b = 5,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,a = 2.) Таким образом: (fleft( x right) = {log _2}left( {x + 5} right)) и (fleft( {27} right) = {log _2}left( {27 + 5} right) = 5.) Ответ: 5.
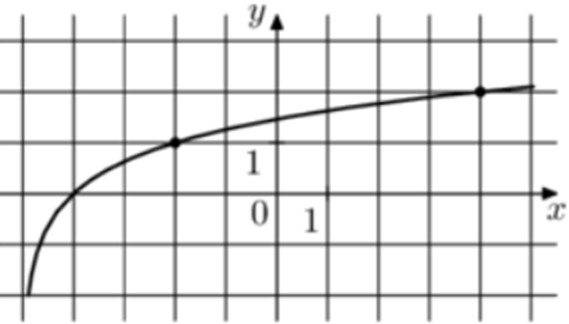
Задача 10. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {238} right).) Ответ ОТВЕТ: 5.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( { — 2;1} right)) и (left( { — 4;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = {{log }_a}left( { — 2 + b} right)}\{0 = {{log }_a}left( { — 4 + b} right)}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{a = — 2 + b}\{ — 4 + b = 1}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 5,,,,,,,a = 3.) Таким образом: (fleft( x right) = {log _3}left( {x + 5} right)) и (fleft( {238} right) = {log _3}left( {238 + 5} right) = 5.) Ответ: 5.
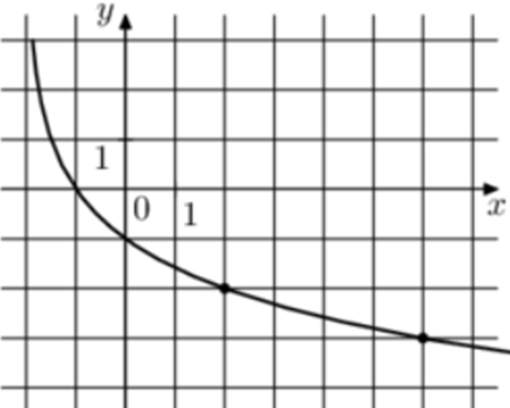
Задача 11. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {30} right).) Ответ ОТВЕТ: — 5.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( {2; — 2} right)) и (left( { — 1;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = {{log }_a}left( {2 + b} right)}\{0 = {{log }_a}left( { — 1 + b} right)}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,left{ {begin{array}{{20}{c}}{{a^{ — 2}} = 2 + b}\{ — 1 + b = 1}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{frac{1}{{{a^2}}} = 2 + b}\{b = 2,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,,,a = frac{1}{2}.) Таким образом: (fleft( x right) = {log _{frac{1}{2}}}left( {x + 2} right)) и (fleft( {30} right) = {log _{frac{1}{2}}}left( {30 + 2} right) = — 5.) Ответ: – 5.
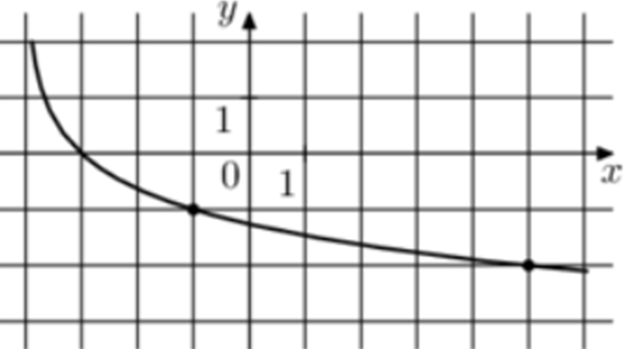
Задача 12. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {77} right).) Ответ ОТВЕТ: — 4.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( { — 1; — 1} right)) и (left( { — 3;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = {{log }_a}left( { — 1 + b} right)}\{0 = {{log }_a}left( { — 3 + b} right)}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,left{ {begin{array}{{20}{c}}{frac{1}{a} = — 1 + b}\{ — 3 + b = 1}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{a = frac{1}{{b — 1}}}\{b = 4,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,,,a = frac{1}{3}.) Таким образом: (fleft( x right) = {log _{frac{1}{3}}}left( {x + 4} right)) и (fleft( {77} right) = {log _{frac{1}{3}}}left( {77 + 4} right) = — 4.) Ответ: – 4.
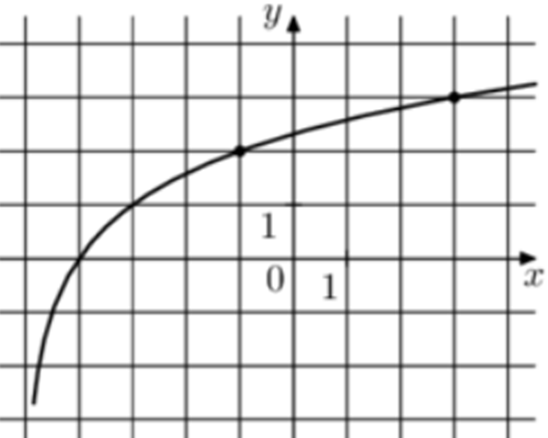
Задача 13. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = 6.) Ответ ОТВЕТ: 59.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( { — 1;2} right)) и (left( { — 4;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = {{log }_a}left( { — 1 + b} right)}\{0 = {{log }_a}left( { — 4 + b} right)}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,left{ {begin{array}{{20}{c}}{{a^2} = — 1 + b}\{ — 4 + b = 1}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{{a^2} = — 1 + b}\{b = 5,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,,,a = 2.) Таким образом: (fleft( x right) = {log _2}left( {x + 5} right)) и ({log _2}left( {x + 5} right) = 6,,,,,,,, Leftrightarrow ,,,,,,,x + 5 = 64,,,,,,,, Leftrightarrow ,,,,,,,,,x = 59.) Ответ: 59.
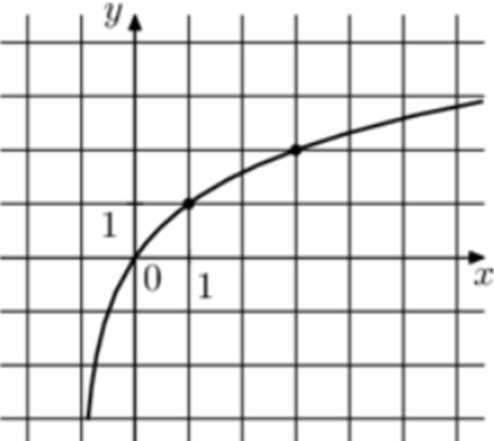
Задача 14. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = 5.) Ответ ОТВЕТ: 31.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( {1;1} right)) и (left( {0;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = {{log }_a}left( {1 + b} right)}\{0 = {{log }_a}b,,,,,,,,,,,,}end{array}} right.,,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{1 + b = a}\{b = 1,,,,,}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 2.) Таким образом: (fleft( x right) = {log _2}left( {x + 1} right)) и ({log _2}left( {x + 1} right) = 5,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 32,,,,,,,, Leftrightarrow ,,,,,,,,,x = 31.) Ответ: 31.
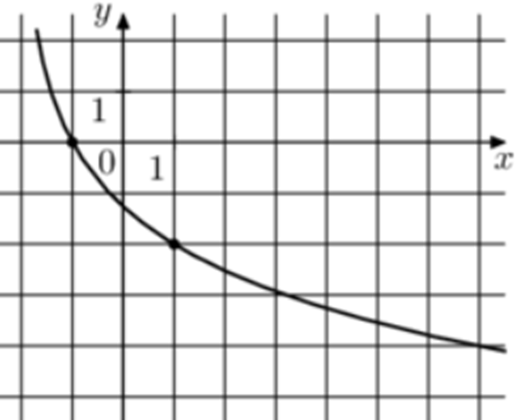
Задача 15. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = — 8.) Ответ ОТВЕТ: 79.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( {1; — 2} right)) и (left( { — 1;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = {{log }_a}left( {1 + b} right)}\{0 = {{log }_a}left( { — 1 + b} right)}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,left{ {begin{array}{{20}{c}}{{a^{ — 2}} = 1 + b}\{ — 1 + b = 1}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{frac{1}{{{a^2}}} = 1 + b}\{b = 2,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,,,b = frac{1}{{sqrt 3 }}.) Таким образом: (fleft( x right) = {log _{frac{1}{{sqrt 3 }}}}left( {x + 2} right)) и ({log _{frac{1}{{sqrt 3 }}}}left( {x + 2} right) = — 8,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 81,,,,,,,, Leftrightarrow ,,,,,,,,,x = 79.) Ответ: 79.
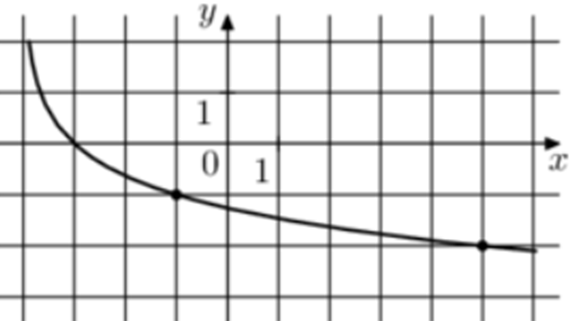
Задача 16. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = — 5.) Ответ ОТВЕТ: 239.
Решение График логарифмический функции (fleft( x right) = {log _a}left( {x + b} right)) проходит через точки (left( { — 1; — 1} right)) и (left( { — 3;0} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = {{log }_a}left( { — 1 + b} right)}\{0 = {{log }_a}left( { — 3 + b} right)}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,left{ {begin{array}{{20}{c}}{{a^{ — 1}} = b — 1}\{ — 3 + b = 1}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{a = frac{1}{{b — 1}}}\{b = 4,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,,,a = frac{1}{3}.) Таким образом: (fleft( x right) = {log _{frac{1}{3}}}left( {x + 4} right)) и ({log _{frac{1}{3}}}left( {x + 4} right) = — 5,,,,,,,, Leftrightarrow ,,,,,,,x + 4 = 243,,,,,,,, Leftrightarrow ,,,,,,,,,x = 239.) Ответ: 239.

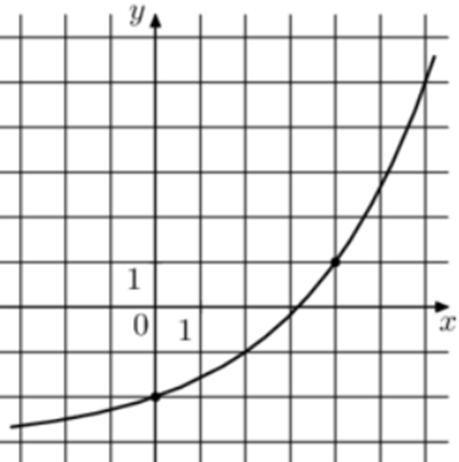
Задача 17. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( {10} right).) Ответ ОТВЕТ: 29.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 2} right)) и (left( {4;1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = {a^0} + b}\{1 = {a^4} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 3,,,,,,}\{1 = {a^4} + b}end{array}} right.,,,,,, Leftrightarrow ,,,,,,,,{a^4} = 4,,,,,,,, Leftrightarrow ,,,,,,,,a = sqrt 2 .) Таким образом: (fleft( x right) = {sqrt 2 ^x} — 3) и (fleft( {10} right) = {sqrt 2 ^{10}} — 3 = 29.) Ответ: 29.
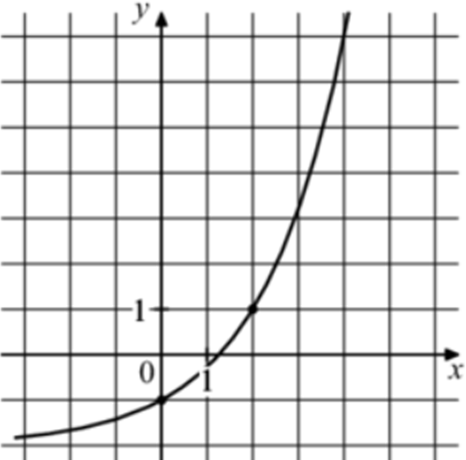
Задача 18. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( 8 right).) Ответ ОТВЕТ: 79.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 1} right)) и (left( {2;1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = {a^0} + b}\{1 = {a^2} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 2,,,,,,}\{1 = {a^2} + b}end{array}} right.,,,,,, Leftrightarrow ,,,,,,,,{a^2} = 3,,,,,,,, Leftrightarrow ,,,,,,,,a = sqrt 3 .) Таким образом: (fleft( x right) = {sqrt 3 ^x} — 2) и (fleft( 8 right) = {sqrt 3 ^8} — 2 = 79.) Ответ: 79.
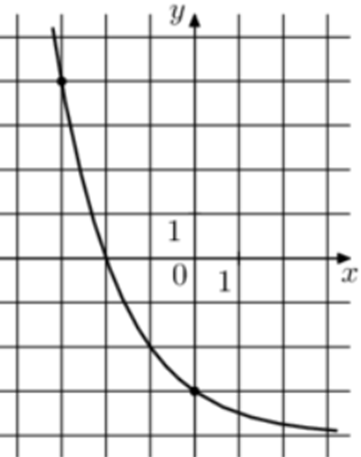
Задача 19. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 28.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 3} right)) и (left( { — 1; — 2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 3 = {a^0} + b}\{ — 2 = {a^{ — 1}} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 4,,,,,,}\{ — 2 = frac{1}{a} + b}end{array}} right.,,,,,, Leftrightarrow ,,,,,,,,a = frac{1}{2}.) Таким образом: (fleft( x right) = {left( {frac{1}{2}} right)^x} — 4) и (fleft( { — 5} right) = {left( {frac{1}{2}} right)^{ — 5}} — 4 = 32 — 4 = 28.) Ответ: 28.
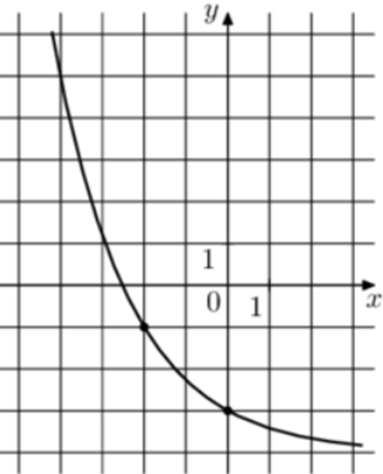
Задача 20. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( { — 8} right).) Ответ ОТВЕТ: 77.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 3} right)) и (left( { — 2; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 3 = {a^0} + b}\{ — 1 = {a^{ — 2}} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 4,,,,,,}\{ — 1 = frac{1}{{{a^2}}} + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,,,frac{1}{{{a^2}}} = 3,,,,,,,, Leftrightarrow ,,,,,,,,a = frac{1}{{sqrt 3 }}.) Таким образом: (fleft( x right) = {left( {frac{1}{{sqrt 3 }}} right)^x} — 4) и (fleft( { — 8} right) = {left( {frac{1}{{sqrt 3 }}} right)^{ — 8}} — 4 = 81 — 4 = 77.) Ответ: 77.
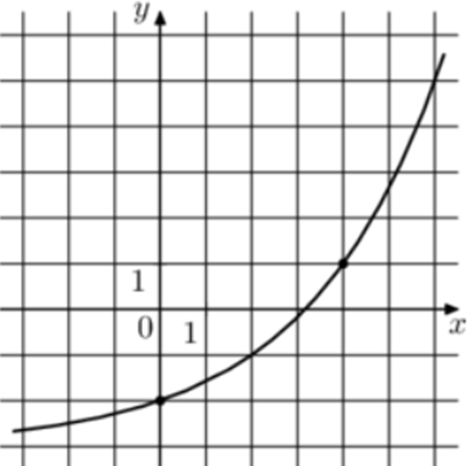
Задача 21. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 13.) Ответ ОТВЕТ: 8.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 2} right)) и (left( {4;1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = {a^0} + b}\{1 = {a^4} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 3,,,,,,}\{1 = {a^4} + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,,,{a^4} = 4,,,,,,,, Leftrightarrow ,,,,,,,,a = sqrt 2 .) Таким образом: (fleft( x right) = {sqrt 2 ^x} — 3) и ({left( {sqrt 2 } right)^x} — 3 = 13,,,,,,, Leftrightarrow ,,,,,,,,{2^{frac{x}{2}}} = 16,,,,,,,,, Leftrightarrow ,,,,,,,,,,x = 8.) Ответ: 8.
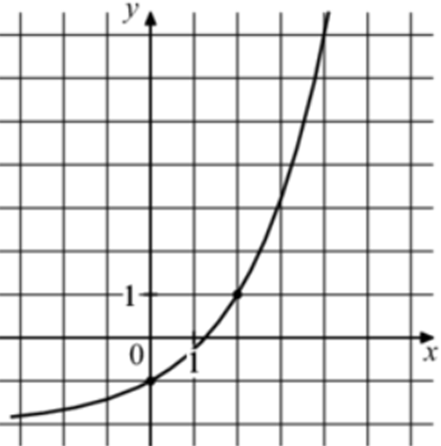
Задача 22. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 25.) Ответ ОТВЕТ: 6.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 1} right)) и (left( {2;1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = {a^0} + b}\{1 = {a^2} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 2,,,,,,}\{1 = {a^2} + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,,,{a^2} = 3,,,,,,,, Leftrightarrow ,,,,,,,,a = sqrt 3 .) Таким образом: (fleft( x right) = {sqrt 3 ^x} — 2) и ({sqrt 3 ^x} — 2 = 25,,,,,,, Leftrightarrow ,,,,,,,,{3^{frac{x}{2}}} = 27,,,,,,,,, Leftrightarrow ,,,,,,,,,,x = 6.) Ответ: 6.
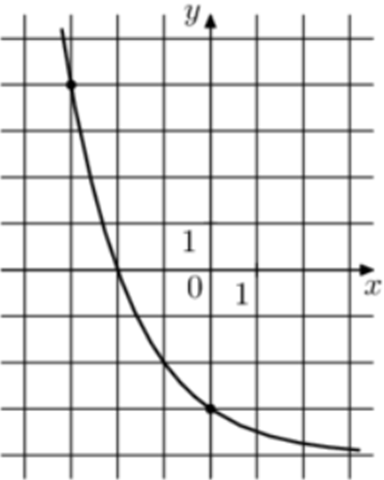
Задача 23. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 12.) Ответ ОТВЕТ: — 4.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 3} right)) и (left( { — 1; — 2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 3 = {a^0} + b}\{ — 2 = {a^{ — 1}} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 4,,,,,,}\{ — 2 = frac{1}{a} + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,,,frac{1}{a} = 2,,,,,,,, Leftrightarrow ,,,,,,,,a = frac{1}{2}.) Таким образом: (fleft( x right) = {left( {frac{1}{2}} right)^x} — 4) и ({left( {frac{1}{2}} right)^x} — 4 = 12,,,,,,, Leftrightarrow ,,,,,,,,{2^{ — x}} = 16,,,,,,,,, Leftrightarrow ,,,,,,,,,,x = — 4.) Ответ: – 4.
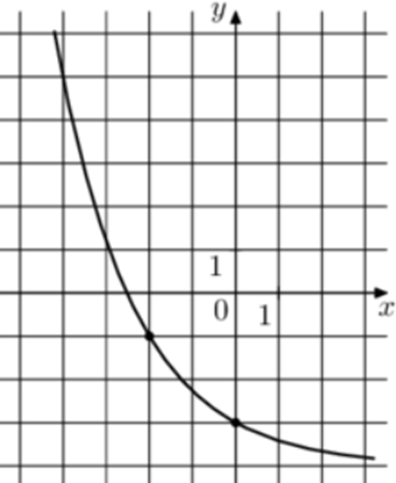
Задача 24. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 23.) Ответ ОТВЕТ: — 6.
Решение График показательной функции (fleft( x right) = {a^x} + b) проходит через точки (left( {0; — 3} right)) и (left( { — 2; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 3 = {a^0} + b}\{ — 1 = {a^{ — 2}} + b}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{{20}{c}}{b = — 4,,,,,,}\{ — 1 = frac{1}{{{a^2}}} + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,,,frac{1}{{{a^2}}} = 3,,,,,,,, Leftrightarrow ,,,,,,,,a = frac{1}{{sqrt 3 }}.) Таким образом: (fleft( x right) = {left( {frac{1}{{sqrt 3 }}} right)^x} — 4) и ({left( {frac{1}{{sqrt 3 }}} right)^x} — 4 = 23,,,,,,, Leftrightarrow ,,,,,,,,{3^{ — frac{x}{2}}} = {3^3},,,,,,,,, Leftrightarrow ,,,,,,,,,,x = — 6.) Ответ: – 6.
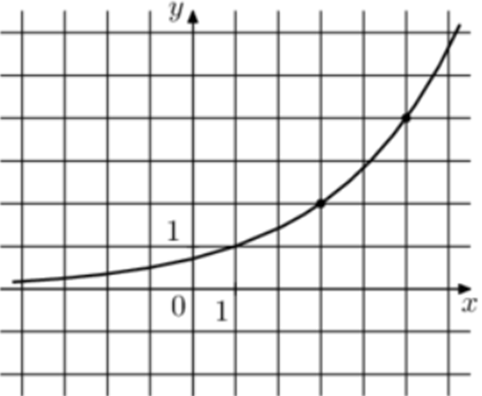
Задача 25. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 0,125.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( {3;2} right)) и (left( {5;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = {a^{3 + b}}}\{4 = {a^{5 + b}}}end{array}} right.) Разделим второе уравнение на первое: (frac{{{a^{5 + b}}}}{{{a^{3 + b}}}} = frac{4}{2},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^2} = 2,,,,,,,,, Leftrightarrow ,,,,,,,,,a = sqrt 2 .) Тогда: ({sqrt 2 ^{3 + b}} = 2,,,,,,,,, Leftrightarrow ,,,,,,,,,{2^{frac{{3 + b}}{2}}} = {2^1},,,,,,, Leftrightarrow ,,,,,,,,frac{{3 + b}}{2} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,b = — 1.) Таким образом: (fleft( x right) = {sqrt 2 ^{,x — 1}}) и (fleft( { — 5} right) = {sqrt 2 ^{ ,- 5 — 1}} = {2^{frac{1}{2} cdot left( { — 6} right)}} = {2^{ — 3}} = frac{1}{8} = 0,125.) Ответ: 0,125.
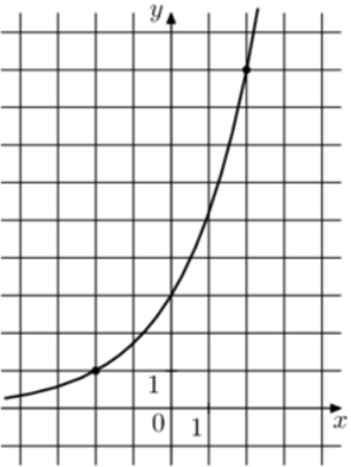
Задача 26. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( 6 right).) Ответ ОТВЕТ: 81.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( { — 2;1} right)) и (left( {2;9} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = {a^{ — 2 + b}}}\{9 = {a^{2 + b}}}end{array}} right.) Разделим второе уравнение на первое: (frac{{{a^{2 + b}}}}{{{a^{ — 2 + b}}}} = frac{9}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^4} = 9,,,,,,,,, Leftrightarrow ,,,,,,,,,a = sqrt 3 .) Тогда: ({sqrt 3 ^{ ,- 2 + b}} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,,{sqrt 3 ^{ ,- 2 + b}} = {sqrt 3 ^0},,,,,,, Leftrightarrow ,,,,,,,, — 2 + b = 0,,,,,,,,, Leftrightarrow ,,,,,,,,b = 2.) Таким образом: (fleft( x right) = {sqrt 3 ^{,x + 2}}) и (fleft( 6 right) = {sqrt 3 ^{,6 + 2}} = {sqrt 3 ^8} = {3^4} = 81.) Ответ: 81.
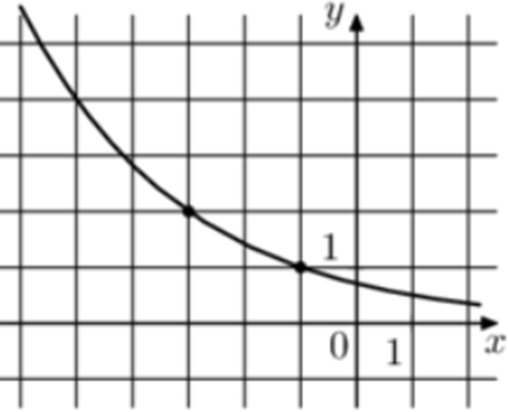
Задача 27. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 9} right).) Ответ ОТВЕТ: 16.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( { — 1;1} right)) и (left( { — 3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = {a^{ — 1 + b}}}\{2 = {a^{ — 3 + b}}}end{array}} right.) Разделим первое уравнение на второе: (frac{{{a^{, — 1 + b}}}}{{{a^{, — 3 + b}}}} = frac{1}{2},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^2} = frac{1}{2},,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{{sqrt 2 }}.) Тогда: ({left( {frac{1}{{sqrt 2 }}} right)^{, — 1 + b}} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,,{left( {frac{1}{{sqrt 2 }}} right)^{, — 1 + b}} = {left( {frac{1}{{sqrt 2 }}} right)^0},,,,,,, Leftrightarrow ,,,,,,,, — 1 + b = 0,,,,,,,,, Leftrightarrow ,,,,,,,,b = 1.) Таким образом: (fleft( x right) = {left( {frac{1}{{sqrt 2 }}} right)^{,x + 1}}) и (fleft( { — 9} right) = {left( {frac{1}{{sqrt 2 }}} right)^{, — 9 + 1}} = {left( {frac{1}{{sqrt 2 }}} right)^{, — 8}} = {2^4} = 16.) Ответ: 16.
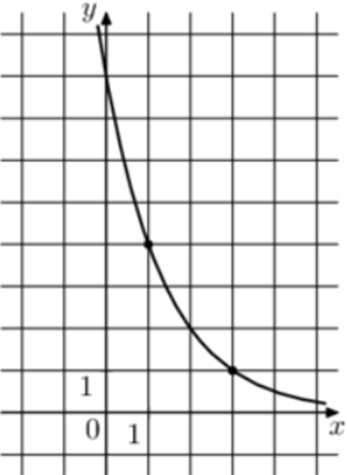
Задача 28. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 2} right).) Ответ ОТВЕТ: 32.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( {1;4} right)) и (left( {3;1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = {a^{1 + b}}}\{1 = {a^{3 + b}}}end{array}} right.) Разделим второе уравнение на первое: (frac{{{a^{3 + b}}}}{{{a^{1 + b}}}} = frac{1}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^2} = frac{1}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ({left( {frac{1}{2}} right)^{3 + b}} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,,{left( {frac{1}{2}} right)^{3 + b}} = {left( {frac{1}{2}} right)^0},,,,,,, Leftrightarrow ,,,,,,,,3 + b = 0,,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3.) Таким образом: (fleft( x right) = {left( {frac{1}{2}} right)^{x — 3}}) и (fleft( { — 2} right) = {left( {frac{1}{2}} right)^{ — 2 — 3}} = {2^5} = 32.) Ответ: 32.
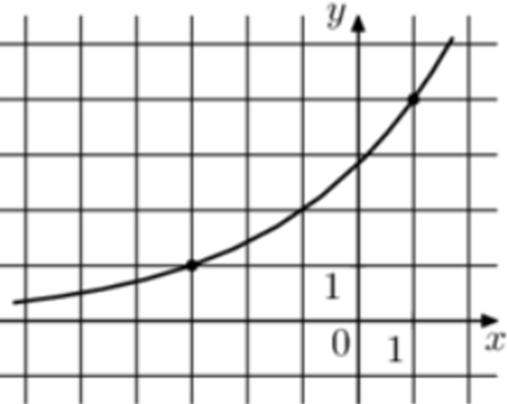
Задача 29. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 16.) Ответ ОТВЕТ: 5.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( {1;4} right)) и (left( { — 3;1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = {a^{1 + b}}}\{1 = {a^{ — 3 + b}}}end{array}} right.) Разделим первое уравнение на второе: (frac{{{a^{1 + b}}}}{{{a^{ — 3 + b}}}} = frac{4}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^4} = 4,,,,,,,,, Leftrightarrow ,,,,,,,,,a = sqrt 2 .) Тогда: ({left( {sqrt 2 } right)^{ — 3 + b}} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,,{left( {sqrt 2 } right)^{ — 3 + b}} = {sqrt 2 ^0},,,,,,, Leftrightarrow ,,,,,,,, — 3 + b = 0,,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Таким образом: (fleft( x right) = {sqrt 2 ^{,x + 3}}) и ({sqrt 2 ^{,x + 3}} = 16,,,,,, Leftrightarrow ,,,,,,,{2^{frac{{x + 3}}{2}}} = {2^4},,,,,, Leftrightarrow ,,,,,,,,frac{{x + 3}}{2} = 4,,,,,,, Leftrightarrow ,,,,,,,,,x = 5.) Ответ: 5.
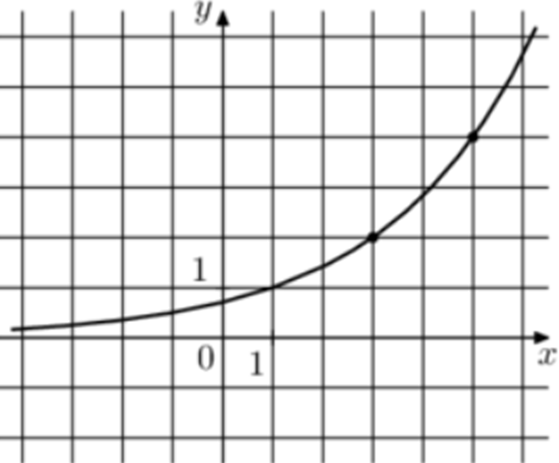
Задача 30. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 0,125.) Ответ ОТВЕТ: — 5.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( {3;2} right)) и (left( {5;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = {a^{3 + b}}}\{4 = {a^{5 + b}}}end{array}} right.) Разделим второе уравнение на первое: (frac{{{a^{5 + b}}}}{{{a^{3 + b}}}} = frac{4}{2},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^2} = 2,,,,,,,,, Leftrightarrow ,,,,,,,,,a = sqrt 2 .) Тогда: ({sqrt 2 ^{,3 + b}} = 2,,,,,,,,, Leftrightarrow ,,,,,,,,,{sqrt 2 ^{,3 + b}} = {sqrt 2 ^{,2}},,,,,,, Leftrightarrow ,,,,,,,,3 + b = 2,,,,,,,,, Leftrightarrow ,,,,,,,,b = — 1.) Таким образом: (fleft( x right) = {sqrt 2 ^{,x — 1}}) и ({sqrt 2 ^{,x — 1}} = frac{1}{8},,,,,,,,, Leftrightarrow ,,,,,,,,{2^{frac{{x — 1}}{2}}} = {2^{ — 3}},,,,,,, Leftrightarrow ,,,,,,,,,x = — 5.) Ответ: – 5.
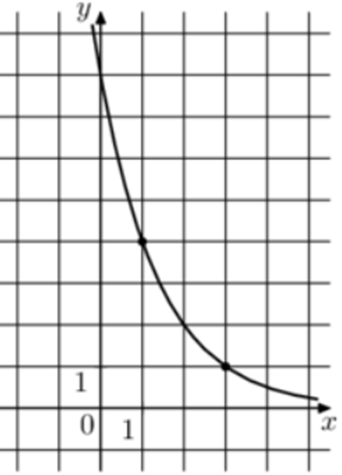
Задача 31. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 64.) Ответ ОТВЕТ: — 3.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( {3;1} right)) и (left( {1;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = {a^{3 + b}}}\{4 = {a^{1 + b}}}end{array}} right.) Разделим первое уравнение на второе: (frac{{{a^{3 + b}}}}{{{a^{1 + b}}}} = frac{1}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^2} = frac{1}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ({left( {frac{1}{2}} right)^{3 + b}} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,,{left( {frac{1}{2}} right)^{3 + b}} = {left( {frac{1}{2}} right)^0},,,,,,, Leftrightarrow ,,,,,,,,3 + b = 0,,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3.) Таким образом: (fleft( x right) = {left( {frac{1}{2}} right)^{x — 3}}) и ({left( {frac{1}{2}} right)^{x — 3}} = 64,,,,,, Leftrightarrow ,,,,,,,{left( {frac{1}{2}} right)^{x — 3}} = {left( {frac{1}{2}} right)^{ — 6}},,,,,, Leftrightarrow ,,,,,,,,x — 3 = — 6,,,,,,, Leftrightarrow ,,,,,,,,,x = — 3.) Ответ: – 3.
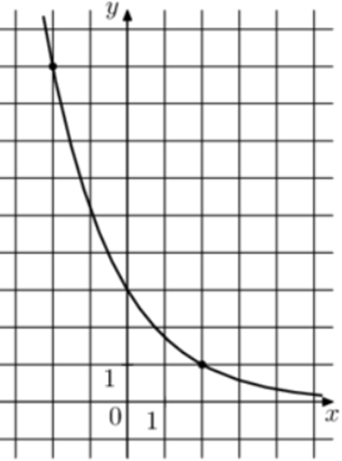
Задача 32. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 81.) Ответ ОТВЕТ: — 6.
Решение График показательной функции (fleft( x right) = {a^{x + b}}) проходит через точки (left( { — 2;9} right)) и (left( {2;1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{9 = {a^{ — 2 + b}}}\{1 = {a^{2 + b}}}end{array}} right.) Разделим второе уравнение на первое: (frac{{{a^{2 + b}}}}{{{a^{ — 2 + b}}}} = frac{1}{9},,,,,,,,, Leftrightarrow ,,,,,,,,,{a^4} = frac{1}{9},,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{{sqrt 3 }}.) Тогда: ({left( {frac{1}{{sqrt 3 }}} right)^{2 + b}} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,,{left( {frac{1}{{sqrt 3 }}} right)^{2 + b}} = {left( {frac{1}{{sqrt 3 }}} right)^0},,,,,,, Leftrightarrow ,,,,,,,,2 + b = 0,,,,,,,,, Leftrightarrow ,,,,,,,,b = — 2.) Таким образом: (fleft( x right) = {left( {frac{1}{{sqrt 3 }}} right)^{x — 2}}) и ({left( {frac{1}{{sqrt 3 }}} right)^{x — 2}} = 81,,,,,,,,, Leftrightarrow ,,,,,,,,{3^{ — ,frac{{x — 2}}{2}}} = {2^4},,,,,,, Leftrightarrow ,,,,,,,,,,, — ,,frac{{x — 2}}{2} = 4,,,,,,,,, Leftrightarrow ,,,,,,,,,x = — 6.) Ответ: – 6.

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Логарифмические функции»

Открытый банк заданий по теме логарифмические функции. Задания B12 из ЕГЭ по математике (профильный уровень)

Тригонометрические уравнения

Задание №1132

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=5x^2-12x+2ln x+37 на отрезке left[frac35; frac75right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 10x-12+frac{2}{x}= frac{10x^2-12x+2}{x}.

Определим нули производной: y'(x)=0;

frac{10x^2-12x+2}{x}=0,

5x^2-6x+1=0,

x_{1,2}= frac{3pmsqrt{3^2-5cdot1}}{5}= frac{3pm2}{5},

x_1=frac15notinleft[frac35; frac75right],

x_2=1inleft[frac35; frac75right].

Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом промежутке.

Из рисунка видно, что на отрезке left[frac35; 1right]исходная функция убывает, а на отрезке left[1; frac75right]возрастает. Таким образом, наименьшее значение на отрезке left[frac35; frac75right]достигается при x=1 и равно y(1)= 5cdot 1^2-12cdot 1+2 ln 1+37= 30.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1124

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=4x^2-19x+11ln x+715 на отрезке left[frac34; frac54right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 8x-19+frac{11}{x}= frac{8x^2-19x+11}{x}.

Определим нули производной: y'(x)=0;

frac{8x^2-19x+11}{x}=0,

8x^2-19x+11=0,

x_{1,2}= frac{19pmsqrt{19^2-4cdot8cdot11}}{2cdot8}= frac{19pm3}{16},

x_1=1,

x_1in left[frac34; frac54right],

x_2=frac{22}{16}=frac{11}{8}>frac{10}{8}=frac{5}{4},

x_2notin left[frac34; frac54right].

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что на отрезке left[frac34; 1right] исходная функция возрастает, а на отрезке left[1; frac54right] убывает. Таким образом, наибольшее значение на отрезке left[frac34; frac54right] достигается при x=1 и равно y(1)= 4cdot 1^2-19cdot 1+11 ln 1+715= 700.

Ответ

700

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1116

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=7x-ln(x+11)^7 на отрезке [-10,5;,,0].

Показать решение

Решение

ОДЗ: (x+11)^7>0, x+11>0, x>-11. На ОДЗ исходная функция примет вид:y=7x-7 ln (x+11).

Найдём производную: y’=7-frac{7}{x+11}. Определим нули производной: 7-frac{7}{x+11}=0,

frac{1}{x+11}=1,

x=-10.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что на отрезке [-10,5; -10] исходная функция убывает, а на отрезке [-10; 0] возрастает. Таким образом, наименьшее значение на отрезке [-10,5; 0] достигается при x=-10 и равно y(-10)= 7cdot (-10)-ln (-10+11)^7= -70.

Ответ

-70

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №952

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+7)^9-9x на отрезке [-6,5; 0].

Показать решение

Решение

ОДЗ. (x+7)^9>0, x+7>0, x>-7.

Так как на ОДЗ ln(x+7)^9=9ln(x+7), то исходная функция примет вид: y=9ln(x+7)-9x. Найдём производную: y’=frac{9}{x+7}-9.

Определим нули производной

frac{9}{x+7}-9=0,

frac{1}{x+7}=1,

x=-6.

Расставим знаки производной и определим промежутки монотонности исходной функции

Из рисунка видно, что на отрезке [-6,5; -6] исходная функция возрастает, а на отрезке [-6; 0] — убывает. Таким образом, наибольшее значение на отрезке [-6,5; 0] достигается при x=-6 и равно y(-6)=ln(-6+7)^9-9cdot(-6)=54.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №336

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=12x-ln(12x)+100 на отрезке left [frac{1}{36}; frac34 right ].

Показать решение

Решение

y’=(12x-ln(12x)+100)’=12-frac{12}{12x}=frac{12x-1}{x}.

y’=0 при x=frac{1}{12}, причем y’ меняет знак в этой точке с «−» на «+». Это означает, что x=frac{1}{12} является точкой минимума.

yleft ( frac{1}{12} right )=12cdotfrac{1}{12}-lnleft ( 12cdotfrac{1}{12} right )+100=1-0+100=101.

Ответ

101

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №125

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+8)^3-3x на отрезке [−7,5; 0]

Показать решение

Решение

Выполним преобразования и вычислим производную.

y=3ln(x+8)-3x

y’=frac{3}{x+8}-3

Найдем точки экстремума, в которых производная функции обращается в нуль.

frac{3}{x+8}=3

x+8=1

x=-7

На числовой оси расставим знаки производной и посмотрим как ведет себя функция.

При переходе через точку x = −7 производная меняет знак с плюса на минус. Значит x = −7 – точка максимума функции.

Найдем наибольшее значение функции в точке x = −7.

y(-7)=3ln1+21=21

Наибольшее значение функции равно 21.

Ответ

Задание №124

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите точку максимума функции y=log_2(4+10x-x^2)-71.

Показать решение

Решение

Определим область допустимых значений функции.

4+10x-x^2>0

x^2-10x-4<0

5-sqrt{29}<x<5+sqrt{29}

Вычислим производную функции.

y’=frac{10-2x}{(4+10x-x^2)ln2}

Найдем точки экстремума, в которых производная функции обращается в нуль.

10-2x=0

x = 5

На числовой оси отложим граничные точки ОДЗ и точку экстремума и посмотрим как ведет себя функция.

При переходе через точку x = 5 производная меняет знак с плюса на минус. Значит x = 5 – точка максимума функции.

Ответ

Задание №123

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+5)^4-4x на отрезке [−4,5; 0].

Показать решение

Решение

Выполним преобразования и вычислим производную.

y=4ln(x+5)-4x

y’=frac{4}{x+5}-4

Найдем точки экстремума, в которых производная функции обращается в нуль.

frac{4}{x+5}=4

x+5=1

x=-4

На числовой оси отложим граничные точки отрезка и точку экстремума и посмотрим как ведет себя функция.

При переходе через точку x = −4 производная меняет знак с плюса на минус. Значит x = −4 – точка максимума функции.

Найдем наибольшее значение функции в точке x = −4.

y(-4)=ln(-4+5)^4-4cdot(-4)=16

Наибольшее значение функции равно 16.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

14 января 2018

В закладки

Обсудить

Жалоба

Логарифмы в заданиях ЕГЭ

Большая часть заданий, включенных в ЕГЭ, представляет собой задания на вычисление значений числовых логарифмических выражений.

При подготовке следует обратить внимание на формулу перехода к новому основанию логарифма и следствия из нее. Задачи на использование этих формул в школьных учебниках практически не встречаются.

Материал для проведения самостоятельных работ. 15 вариантов по 28 заданий. Ответы прилагаются.

log-sm.docx

Источник