Решу егэ логические высказывания - Помощь в подготовке к экзаменам и поступлению

Каталог заданий
Задания Д15. Преобразование логических выражений. Логические высказывания

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д15 № 701

Для какого имени ложно высказывание:

(Первая буква имени гласная → Четвертая буква имени согласная).

1)  ЕЛЕНА

2)  ВАДИМ

3)  АНТОН

4)  ФЕДОР

Задания Д15 № 723

Для какого имени истинно высказывание:

Третья буква гласная → ¬ (Первая буква согласная / В слове 4 гласных буквы)?

1)  Римма

2)  Анатолий

3)  Светлана

4)  Дмитрий

Задания Д15 № 710

Логическое выражение ¬Y / ¬((Х V Y) Λ ¬Y) Λ Х Λ ¬Y максимально упpощаетcя до выражения

1)  Х Λ Y

2)  ¬Y

3)  Х

4)  1

Задания Д15 № 801

Какое логическое выражение равносильно выражению ¬ (А / ¬B)?

1)  A / B

2)  A / B

3)  ¬A / ¬B

4)  ¬A / B

Задания Д15 № 802

Какое логическое выражение равносильно выражению ¬ (¬A / ¬B) / C

1)  ¬A / B / ¬C

2)  А / B / C

3)  (A / B) / C

4)  (¬A / ¬B) / ¬C

Пройти тестирование по этим заданиям

Источник

Всего: 191 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.

Так, например, 14&5  =  1110₂&0101₂  =  0100₂  =  4.

Для какого наибольшего целого числа А формула

x&51 = 0 ∨ (x&41 = 0 → x&А = 0)

тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.

Так, например, 14&5  =  1110₂&0101₂  =  0100₂  =  4.

Для какого наименьшего неотрицательного целого числа А формула

x&51 = 0 ∨ (x&41 = 0 → x&А = 0)

тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?

На числовой прямой даны два отрезка: P = [17, 46] и Q = [22, 57]. Отрезок A таков, что приведённая ниже формула истинна при любом значении переменной х:

¬(x ∈ A) →(((x ∈ P) ⋀ (x ∈ Q)) → (x ∈ A))

Какова наименьшая возможная длина отрезка A?

На числовой прямой даны два отрезка: Р = [30, 45] и Q = [40, 55]. Какова наименьшая возможная длина интервала A, что обе приведённые ниже формулы истинны при любом значении переменной х:

( ¬(x ∈ A) → (¬(x ∈ P)) )

((x ∈ Q)→ (x ∈ A))

На числовой прямой даны два отрезка: Р = [3, 38] и Q = [21, 57]. Какова наибольшая возможная длина интервала A, что логическое выражение

((х ∈ Q) → (х ∈ Р)) → ¬(х ∈ A)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [1, 39] и Q = [23, 58]. Какова наибольшая возможная длина интервала A, что логическое выражение

((x ∈ P) → ¬(x ∈ Q)) → ¬(x ∈ А)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: D  =  [17; 58] и C  =  [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение

(x ∈ D) → ((¬(x ∈ C)∧ ¬(x ∈ A)) → ¬(x ∈ D))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Источник: Демонстрационная версия ЕГЭ−2022 по информатике

На числовой прямой даны два отрезка: P = [4, 15] и Q = [12, 20].

Укажите наименьшую возможную длину отрезка A, для которого выражение

((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [20, 50] и Q = [30,65]. Отрезок A таков, что формул

¬(x ∈ A) → ((x ∈ P) →¬ (x ∈ Q))

истинна при любом значении переменной x. Какова наименьшая возможная длина отрезка A?

Источник: ЕГЭ по информатике 23.03.2016. Досрочная волна

На числовой прямой задан отрезок A. Известно, что формула

((x ∈ A) → (x² ≤ 100)) ∧ ((x² ≤ 64) → (x ∈ A))

тождественно истинна при любом вещественном x. Какую наименьшую длину может иметь отрезок A?

На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Какова наибольшая возможная длина интервала A, что формула

( (x ∈ А) → (x ∈ P) ) ∨ (x ∈ Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны три отрезка: P = [10, 40], Q = [5, 15] и R = [35, 50]. Какова наименьшая возможная длина промежутка A, что формула

( (x ∈ А) ∨ (x ∈ P) ) ∨ ((x ∈ Q)→ (x ∈ R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [12, 62] и Q = [32, 92].

Какова наименьшая возможная длина интервала A, что формула

(¬(x ∈ А) ∧ (x ∈ Q)) → (x ∈ P)

тождественно истинна, т. е. принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [8, 39] и Q = [23, 58].

Какова наименьшая возможная длина интервала A, при которой выражение

((x ∈ P) ∨ (x ∈ А)) → ((x ∈ Q) ∨ (x ∈ А))

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P  =  [17, 54] и Q  =  [37, 83]. Какова наименьшая возможная длина интервала A, что формула

(x ∈ P) → (((x ∈ Q) ∧ ¬(x ∈ A)) → ¬(x ∈ P))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Источник: ЕГЭ по информатике 2021. Досрочная волна

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {4, 8, 12, 16}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))

На числовой прямой даны два отрезка: Р = [22, 72] и Q = [42, 102]. Какова наименьшая возможная длина интервала A, что логическое выражение

¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: Р = [12, 62] и Q = [52, 92]. Какова наименьшая возможная длина интервала A, что логическое выражение

¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [3, 13] и Q = [12, 22]. Какова наибольшая возможная длина интервала A, что формула

((х ∈ A) → (х ∈ Р)) ∨ (х ∈ Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Всего: 191 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Всего: 191 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.

Так, например, 14&5  =  1110₂&0101₂  =  0100₂  =  4.

Для какого наибольшего целого числа А формула

x&51 = 0 ∨ (x&41 = 0 → x&А = 0)

тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.

Так, например, 14&5  =  1110₂&0101₂  =  0100₂  =  4.

Для какого наименьшего неотрицательного целого числа А формула

x&51 = 0 ∨ (x&41 = 0 → x&А = 0)

тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?

¬(x ∈ A) →(((x ∈ P) ⋀ (x ∈ Q)) → (x ∈ A))

Какова наименьшая возможная длина отрезка A?

( ¬(x ∈ A) → (¬(x ∈ P)) )

((x ∈ Q)→ (x ∈ A))

((х ∈ Q) → (х ∈ Р)) → ¬(х ∈ A)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

((x ∈ P) → ¬(x ∈ Q)) → ¬(x ∈ А)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

(x ∈ D) → ((¬(x ∈ C)∧ ¬(x ∈ A)) → ¬(x ∈ D))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Источник: Демонстрационная версия ЕГЭ−2022 по информатике

На числовой прямой даны два отрезка: P = [4, 15] и Q = [12, 20].

Укажите наименьшую возможную длину отрезка A, для которого выражение

((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [20, 50] и Q = [30,65]. Отрезок A таков, что формул

¬(x ∈ A) → ((x ∈ P) →¬ (x ∈ Q))

истинна при любом значении переменной x. Какова наименьшая возможная длина отрезка A?

Источник: ЕГЭ по информатике 23.03.2016. Досрочная волна

На числовой прямой задан отрезок A. Известно, что формула

((x ∈ A) → (x² ≤ 100)) ∧ ((x² ≤ 64) → (x ∈ A))

тождественно истинна при любом вещественном x. Какую наименьшую длину может иметь отрезок A?

( (x ∈ А) → (x ∈ P) ) ∨ (x ∈ Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

( (x ∈ А) ∨ (x ∈ P) ) ∨ ((x ∈ Q)→ (x ∈ R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [12, 62] и Q = [32, 92].

Какова наименьшая возможная длина интервала A, что формула

(¬(x ∈ А) ∧ (x ∈ Q)) → (x ∈ P)

тождественно истинна, т. е. принимает значение 1 при любом значении переменной х.

На числовой прямой даны два отрезка: P = [8, 39] и Q = [23, 58].

Какова наименьшая возможная длина интервала A, при которой выражение

((x ∈ P) ∨ (x ∈ А)) → ((x ∈ Q) ∨ (x ∈ А))

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

(x ∈ P) → (((x ∈ Q) ∧ ¬(x ∈ A)) → ¬(x ∈ P))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Источник: ЕГЭ по информатике 2021. Досрочная волна

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {4, 8, 12, 16}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))

¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

((х ∈ A) → (х ∈ Р)) ∨ (х ∈ Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Всего: 191 1–20 | 21–40 | 41–60 | 61–80 …

Источник

ЕГЭ по информатике выбирают будущие работники ИТ-сферы. Но для сдачи экзамена нужно не только уметь программировать. Многие задачи связаны с математикой, анализом данных, логикой. Чтобы без проблем решить их на экзамене, необходимо много практиковаться. Вы можете учиться самостоятельно, а можете записаться на курсы подготовки к ЕГЭ и ОГЭ, где преподаватели будут объяснять все сложные моменты. В статье мы разберем тему «Логические выражения». Она встречается в 23 номере ЕГЭ по информатике.

Алгебра логики

Прежде чем приступить к разбору заданий, нужно изучить теорию. Алгеброй логики называют один из разделов математической логики. Его особенность в том, что логические выражения анализируются с использованием алгебраических законов и правил. Создание науки связано с именем Дж. Буля (1815-1864). Ученый разработал собственный математический язык, записывал с его помощью уравнений. Истинность и ложность выражений доказывал с помощью алгебраических операций. Несмотря на то, что алгебра логики продолжает развиваться, принцип остается прежним.

Основой алгебры логики (и 23 задания ЕГЭ) являются логические высказывания — не вопросительные предложения, по поводу которых можно однозначно сказать, являются они истинными или ложными. Например, высказывание «снег белый» истинно, «солнце светит ночью» — ложно. Предложение «мороженое вкусное» не является логическим высказыванием, нельзя однозначно сказать о его правдивости. Если заменить его на «я люблю мороженое», то оно может принимать как истинное, так и ложное значение, это зависит от предпочтений человека.

В 23 задании по информатике встречаются двузначные высказывания, принимающие значения «правда» и «неправда». Но алгебра логики рассматривает также многозначные, имеющие значения «вероятно», «невозможно», «возможно». Элементарные высказывания обозначают латинскими буквами (например, A = «осенью деревья сбрасывают листву»). Сложные высказывания составляются из элементарных с использованием частиц «и», «или», «тогда и только тогда», «если.. то» (например, А и В = «осенью деревья сбрасывают листву и некоторые птицы улетают на юг»). В цифровом представлении истине соответствует число 1, а лжи число 0. Для вычисления примеров обычно используются таблицы истинности.

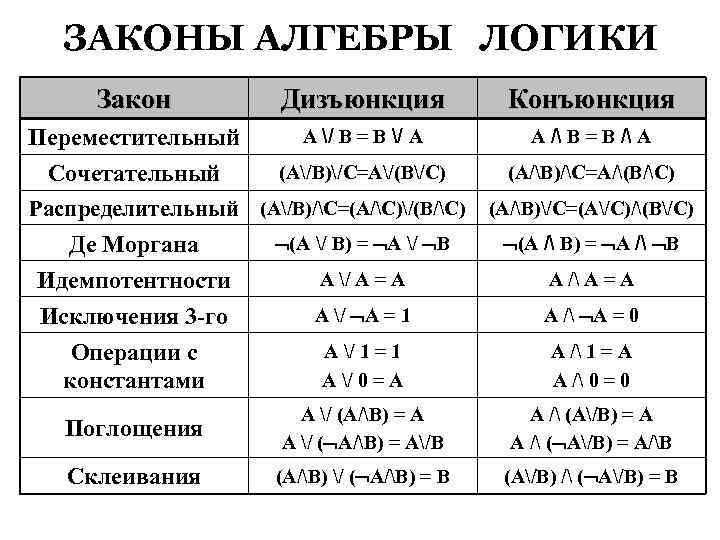
Основные операции алгебры логики

Для решения номера 23 по информатике нужно знать основные операции:

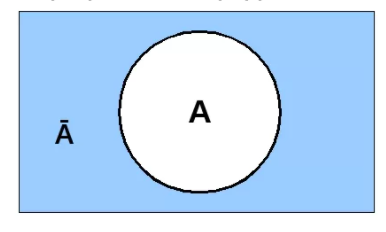
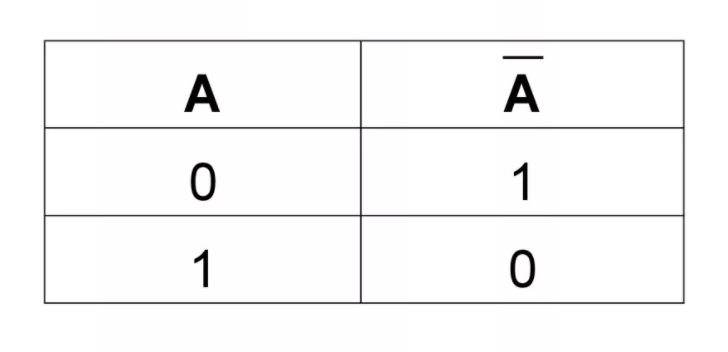
инверсия (отрицание). Операция называется унарной, так как преобразует одну величину: «переворачивает» выражение, меняет истину на ложь и наоборот. Обозначается чертой над буквой, символом ᆨ, словом «not». В результате преобразования числа A получается высказывание ᆨA. Читается «не А», «отрицание А», «А ложно». Пример: A = 1 больше 0; Ā = 1 не больше 0. На рисунке А — множество точек, Ā — все точки, не принадлежащие множеству;

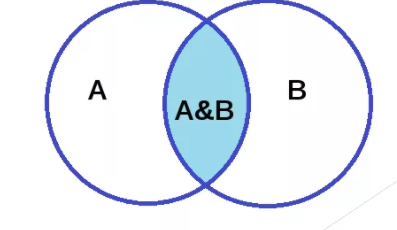
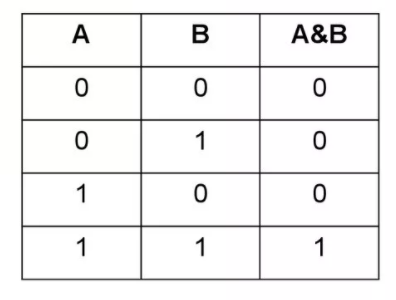
конъюнкция (умножение). Обозначает величины (2 или больше), объединенные союзом И. Для математической записи используются знаки ∧, •, &, and. Иногда знак опускают, по аналогии с математикой. Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;

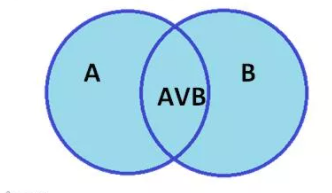
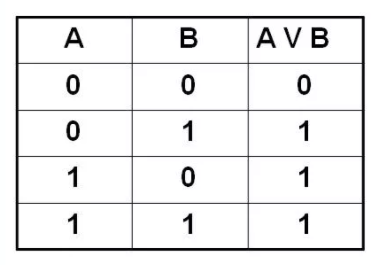
дизъюнкция (сложение). Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;

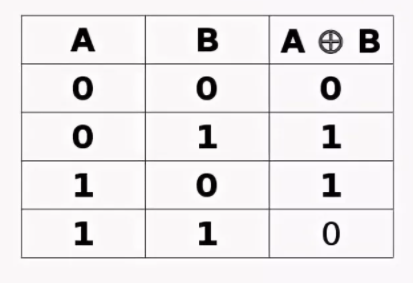
строго-разделительная (исключающая) дизъюнкция. Связывает высказывания союзом ИЛИ. Особенность в том, что союз является исключающим, то есть выражение истинно, когда правдива одна из его частей. Обозначают через ∨∨, ⊕, а читают «либо А, либо В». Пример: А⊕В = «валентность серы II или IV»;

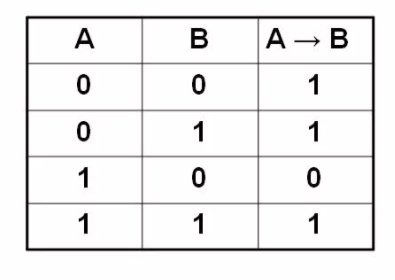
импликация. Соединяет выражения, указывающие на причину и следствие. Обозначается ⟶, ⊃, читается «из А следует В», «если А, то В», «А влечет В». Пример является ложью, когда причина правдива, а следствие — неправда. Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное».

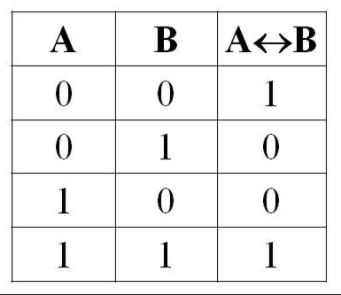
эквивалентность. Операция объединяет высказывания связками ТОГДА И ТОЛЬКО ТОГДА, РАВНОСИЛЬНО, НЕОБХОДИМО И ДОСТАТОЧНО. Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.

На самом деле, для решения номеров достаточно трех операций: сложения, умножения, отрицания. Строго-разделительную дизъюнкцию можно представить как (ᆨА∧B)∧(А∧ᆨВ), импликацию — ᆨА∨B, эквивалентность (ᆨA∧ᆨB)∨(A∧B). Порядок выполнения действий при вычислении:

инверсия;
конъюнкция;
дизъюнкция;
остальные.

Примеры решения задач

Переходим к разбору 23 задания по информатике. Решим несколько задач.

Задача 1. Вычислите логическое значение: (ᆨ(15 < 3))∧(10 > 20).

Решение: Составим таблицу.

15 < 3	10 > 20	ᆨ(15 < 3)	ᆨ(15 < 3)∧(10 > 20)
0	1	1	0

Ответ: ложь.

Задача 2. Запишите высказывание с помощью логических операций, определите его значение: «если часы неправильно показывают время, то вы не успеете на занятия».

Решение: Пусть «часы неправильно показывают время» = А, «успеете на занятия» = В, а «не успеете на занятия» = ᆨВ. Логическое выражение: А⟶ᆨВ. Из причины сделал верный вывод, поэтому выражение является истинным.

Ответ: истина.

Задача 3. Определить значение ((х > 10) ∨ (х < 15)) → (х < 5) для 1) x = 9 и 2) х = 4.

Решение: Для х = 9: ((9 > 10) ∨ (9 < 15)) → (9 < 5) = ложь ∨ истина → ложь = истина → ложь = ложь.

Введите ответ в поле ввода

Решение
→

Задание 7707

Внимательно прочитайте текст задания и выберите верный ответ из списка

Решение
→

Источник

На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи

Содержание:

Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки

2-е задание: «Таблицы истинности»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 3 минуты.

Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы

Типичные ошибки и рекомендации по их предотвращению:

«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»

ФГБНУ «Федеральный институт педагогических измерений»

Таблицы истинности и порядок выполнения логических операций

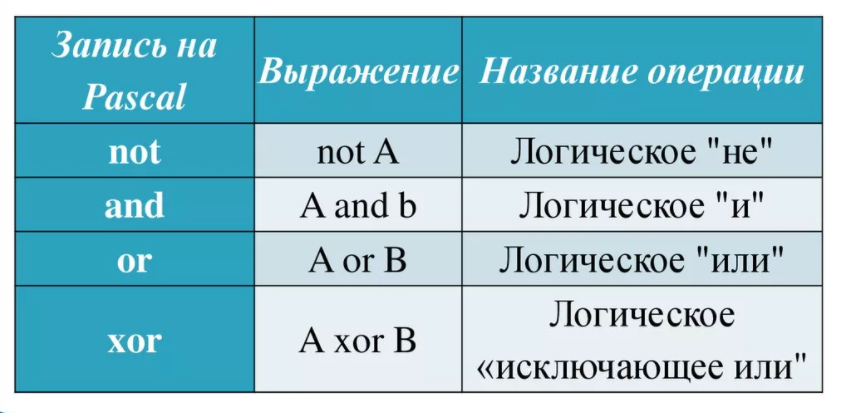
Для логических операций приняты следующие обозначения:

операция	пояснение	в программировании
¬ A, A	не A (отрицание, инверсия)	not(A)
A ∧ B, A ⋅ B	A и B (логическое умножение, конъюнкция)	A and B
A ∨ B, A + B	A или B (логическое сложение, дизъюнкция)	A or B
A → B	импликация (следование)	A <= B
A ↔ B, A ≡ B, A ∼ B	эквиваленция (эквивалентность, равносильность)	A==B (python) A=B(pascal)
A ⊕ B	строгая дизъюнкция	A != B (python) A <> B (pascal)

Егифка ©:

Отрицание (НЕ):

Таблица истинности операции НЕ

Конъюнкция (И):

Таблица истинности операции И (конъюнкция)

Дизъюнкция (ИЛИ):

Таблица истинности операции ИЛИ (дизъюнкция)

Импликация (если…, то…):

Таблица истинности операции Импликация (если…, то…)

Эквивалентность (тогда и только тогда, …):

Таблица истинности операции Эквивалентность (тогда и только тогда, …)

Сложение по модулю 2 (XOR):

A	B	A ⊕ B
0	0	0
0	1	1
1	0	1
1	1	0

Порядок выполнения операций:

если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность

Еще о логических операциях:

логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)

О преобразованиях логических операций читайте здесь.

Егифка ©:

Решение заданий 2 ЕГЭ по информатике

Задание 2_11: Решение 2 задания ЕГЭ по информатике:

Логическая функция F задается выражением

(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

✎ Способ 1. Электронные таблицы Excel + Логические размышления:

Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 2⁴=16:

Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

Выделите таблицу и отсортируйте строки по столбцу с результатом функции. Для этого в меню Главная => Настраиваемая сортировка =>:

Получили верхние строки таблицы — с которыми сравним исходную таблицу и найдем результат:

Получаем следующий порядок переменных:

xwzy

✎ Способ 2. Программирование:

Язык python:

print('x y z w')
for x in 0, 1:
  for y in 0, 1:
    for z in 0, 1:
      for w in 0, 1:
        F = (not(x) or y or z) and (x or not(z) or not(w))
        if not(F):
          print(x, y, z, w)

В результате будут выведены значения для F=0:

Сопоставив их с исходной таблицей, получим результат:

xwzy

Язык pascalAbc.net:

begin
  writeln('x':7, 'y':7, 'z':7,'w':7);
  for var x:=false to true do
    for var y:=false to true do
      for var z:=false to true do
        for var w:=false to true do
          if not((not x or y or z) and (x or not z or not w)) then
            writeln(x:7, y:7, z:7,w:7);
end.

В результате будут выведены значения для F=0:

      x      y      z      w
  False  False   True   True
  False   True   True   True
   True  False  False  False
   True  False  False   True

Где false = 0, True = 1
Сопоставив их с исходной таблицей, получим результат:

Ответ:

xwzy

✎ Способ 3. Логические размышления:

Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:

(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда:
1. (¬x ∨ y ∨ z) = 1 
И 
2. (x ∨ ¬z ∨ ¬w) = 1

Общая идея дальнейшего решения такова: поскольку внешняя операция — конъюнкция, и результат ее истинен, когда оба сомножителя в скобках будут истинны (=1), то нам необходимо сначала составить все наборы таблицы истинности для обоих сомножителей в скобках. Затем, так как конъюнкция подразумевает пересечение, необходимо сопоставить обе таблицы истинности и выбрать для каждого подходящего набора первого сомножителя подходящий (подходящие) набор (наборы) второго сомножителя. НО! так как у нас в задании известны только наборы для F = 0, то мы сопоставлять будем наборы, которые возвращают ложь. Теперь подробно.
Разобьём исходное выражение на две части и составим таблицу истинности отдельно для двух частей.
Для сомножителя (¬x ∨ y ∨ z):

x	y	z	результат
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Получили ложь в одном наборе, так как дизъюнкция (∨) ложна только тогда, когда ложны все операнды.
Для сомножителя (x ∨ ¬z ∨ ¬w):

x	z	w	результат
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Соответственно, опять получили ложь в одном наборе, когда ложны все операнды.
Учтем, что нам нужно выбрать и «пересечь» (так как внешняя операция ∧) из всех наборов только те, которые возвращают ложь (так как по заданию известны только строки, где F = 0):

Выпишем только пересеченные наборы:

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

Сравнив вторую строку заданной таблицы и вторую строку получившейся таблицы, находим, что x находится в первом столбце.

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

x	???	???	???	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Сравнив первую и четвертую одинаковые строки получившейся таблицы, находим, что y в обоих случаях равен 0. Значит он находится в 4-м столбце.

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

x	???	???	y	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Сравнив предпоследнюю и последнюю строки получившейся таблицы, там где x = 1, находим, что z в обоих случаях равен 0, тогда как w принимает значение и 1 и 0. Значит z находится в 3-м столбце.

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

Для w остается второй столбец:

x	w	z	y	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Результат: xwzy

🎦 Видеорешение (бескомпьютерный вариант):

📹 здесь
📹 Видеорешение на RuTube здесь

Задание 2_12: Разбор 2 задания ЕГЭ:

Миша заполнял таблицу истинности функции:

(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)

но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
1	1			0
1		0		0
	1	1	0	0

Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.

Подобные задания для тренировки

✍ Решение:

✎ Способ 1. Логические размышления (бескомпьютерный вариант):

Решим задание методом построения полной таблицы истинности.
Посчитаем общее количество строк в таблице истинности и построим ее:

4 переменных -> 2⁴ = 16 строк

Для начала упростим выражение и выделим в нем две основные части относительно внешней операции (операция, которая выполняется последней).

(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
1. Избавимся от импликации:
¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w)
2. Внесем знак отрицания в скобки (закон Де Моргана):
(z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0
   ^{1 часть = 0     2 часть = 0}

* Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.

Разбили исходное выражение на две части, теперь добавим столбцы для двух частей в таблицу истинности:

Поясним: в первой части внешняя операция — дизъюнкция (ложна, когда оба операнда ложны). Во второй части внешняя операция — конъюнкция — ложна во всех случаях кроме того, когда оба операнда истинны:

(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0

¬y ∧ ¬w = 0 когда:
1. ¬y = 0  ¬w = 0
2. ¬y = 1  ¬w = 0
3. ¬y = 0  ¬w = 1

В результирующей таблице истинности получили только три набора значений переменных при которых выражение возвратит ложь.

x	y	w	z	F
0	1	0	0	0
0	1	1	0	0
1	0	1	0	0

Сравнив их с исходной таблицей истинности, имеем:

y	w	x	z	F
1	1	0	0	0
1	0	0	0	0
0	1	1	0	0

Таким образом, ответ: ywxz

Результат: ywxz

✎ Способ 2. Программирование:

Язык PascalAbc.net:

begin
  writeln('x':7, 'y':7, 'z':7,'w':7);
  for var x:=false to true do
    for var y:=false to true do
      for var z:=false to true do
        for var w:=false to true do
          if not((not z and (x xor y)) <= not(y or w)) then
            writeln(x:7, y:7, z:7,w:7);
end.

В результате будут выведены значения для F=0:

      x      y      z      w
  False   True  False  False
  False   True  False   True
   True  False  False   True

Где false = 0, True = 1

Сопоставив их с исходной таблицей, получим результат: ywxz

Язык Python:

print ('x y z w')
for x in 0,1:
    for y in 0,1:
        for z in 0,1:
            for w in 0,1:
                F=(not z and not(x==y))<=(not(y or w))
                if not F:
                    print (x,y,z,w)

В результате будут выведены значения для F=0:

Сопоставив их с исходной таблицей, получим результат:

Результат: ywxz

🎦 Доступно видео решения этого задания (бескомпьютерный вариант):

📹 здесь
📹 Видеорешение на RuTube здесь

🎦 Видео (решение 2 ЕГЭ в Excel):

📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)

Задание 2_10: Решение 2 задания ЕГЭ по информатике:

Логическая функция F задается выражением

¬a ∧ b ∧ (c ∨ ¬d)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
0	1	0	0	1
1	1	0	0	1
1	1	0	1	1

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:

📹 здесь
📹 Видеорешение на RuTube здесь

Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:

Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
???	???	???	???	F
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Подобные задания для тренировки

✍ Решение:

✎ Логические размышления (бескомпьютерный вариант):

Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:

¬x ∨ y ∨ (¬z ∧ w)

Вспомним таб. ист-ти для дизъюнкции (логическое сложение):

x1	x2	F
0	0	0
0	1	1
1	0	1
1	1	1

Чтобы исходное выражение было истинным, нужно, чтобы хотя бы один из операндов равнялся единице. Т.е. нельзя наверняка сказать, где будет 1, а где 0 (¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).
Функция же ложна только в одном случае, — когда все операнды ложны. Поэтому будем искать по признаку лжи.
В исходной таблице истинности во всех строках функция ложна. Чтобы понять в каком столбце должна находиться та или иная переменная, возьмем за основу строку, в которой только одна единица или только один нуль.
Строка №1: в ней одна единица — первый столбец. В исходной формуле, чтобы функция была ложна, необходимо, чтобы ¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
x	???	???	???	F
1	0	0	0	0

Строка №3: в ней один нуль — четвертый столбец. В исходной формуле, чтобы функция была ложна, необходимо, чтобы y = 0. Значит четвертый столбец соответствует переменной y.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
x	???	???	y	F
1	1	1	0	0

Строка №2: в ней второй столбец равен единице, а третий — нулю. В исходном выражении ¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w.

x	z	w	y	F
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0

Результат: xzwy

✎ Способ 2. Программирование:
Язык pascalABC.NET:

begin
  writeln('x  ','y  ','z  ','w  ');
  for var x:=false to true do
    for var y:=false to true do
      for var z:=false to true do
        for var w:=false to true do
          if not(not x or y or(not z and w)) then
            writeln(x:7,y:7,z:7,w:7);
end.

🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 здесь
📹 Видеорешение на RuTube здесь

Задание 2_13: Разбор досрочного егэ по информатике 2019

Логическая функция F задаётся выражением

(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
0			0	0
0	1	0	1	0
	1	0		0

✍ Решение:

🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь

Задания для тренировки

Задание 2_2: Задание 2 ЕГЭ по информатике:

Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.

Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?

Подобные задания для тренировки

✍ Решение:

Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 2⁵=32, т.е. 32 строки.
Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:

№	F	G	F ∨ G
1	0	0	0
2	0	1	1
…	…	…	1
32	…	…	1

Соответственно, истинными будут все остальные строки:

32 - 1 = 31

Результат: 31

Подробное объяснение данного задания смотрите на видео:

📹 здесь

Задание 2_6: Решение 2 задания ЕГЭ по информатике:

Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.

Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?

✍ Решение:

Полная таблица истинности для каждого из выражений A и B состоит из 2⁷ = 128 строк.
В четырех из них результат равен единице, значит в остальных — 0.
A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:

A	B
1	0
1	0
1	0
1	0
0	1
0	1
0	1
0	1
0	0
…	…

Итого получаем 8 строк.
Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.

Результат: 8

Задание 2_7: Решение 2 задания ЕГЭ по информатике:

Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.

Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?

✍ Решение:

Полная таблица истинности для каждого из выражений A и B состоит из 2⁸ = 256 строк.
В шести из них результат равен единице, значит в остальных — 0.

A ∧ B ложно в том случае, когда:

A ∧ B = 0 если:

1. A = 0, B = 1 
2. B = 0, A = 1
3. A = 0 и B = 0

Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0

A	B	F
1	0	0
1	0	0
1	0	0
1	0	0
0	1	0
0	1	0
0	1	0
0	1	0
0	0	0
…	…	…

Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0

Результат: 256

Задание 2_4: 2 задание:

Дан фрагмент таблицы истинности выражения F.

x1	x2	x3	x4	x5	x6	x7	F
1	0	0	1	1	1	1	0
0	1	0	0	1	0	1	1
0	1	0	1	1	0	1	0

Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7

✍ Решение:

В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:

Но проверим на всякий случай остальные.
Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:

Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:

Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:

Таким образом, ответ равен 1.

Результат: 1

Решение 2 задания ГВЭ по информатике смотрите на видео:

📹 здесь

Задание 2_8: Решение 2 задания ЕГЭ по информатике:

Дано логическое выражение, зависящее от 5 логических переменных:

(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)

Сколько существует различных наборов значений переменных, при которых выражение истинно?

1) 0
2) 30
3) 31
4) 32

Подобные задания для тренировки

✍ Решение:

Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 2⁵ = 32 строк.
Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
Найдем сколько нулей существует для таб. истинности:

Теперь рассмотрим каждый случай отдельно:

1 случай. 0 0 : A = 0 и B = 0, то есть:

¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.

Обратим внимание, что во вторых скобках везде стоит инверсия переменных, которые находятся в первых скобках. Таким образом, это невозможно, так как дизъюнкция равна нулю, когда все операнды равны нулю. А если в первых скобках все 0, то из-за инверсий во вторых скобках все 1. То есть этот случай нам не подходит.
2 случай. 0 1 : нам он подходит, так как если первая скобка возвратит 0, то вторая вернет 1.
3 случай. 1 0 : нам он подходит, так как если вторая скобка возвратит 0, то первая вернет 1.
Итого получаем два случая, когда исходное выражение вернет 0, т.е. две строки таблицы истинности.
Тогда получим количество строк, с результатом равным 1:

32 - 2 = 30, что соответствует номеру 2

Результат: 2

Подробное решение задания смотрите в видеоуроке:

📹 здесь

Задание 2_5: Решение 2 задания ЕГЭ по информатике:

Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	x6	F
0	0	1	1	0	0	1
0	0	0	0	1	1	1
1	0	1	0	1	1	1
0	1	1	1	0	1	0

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.

Подобные задания для тренировки

✍ Решение:

Полная таблица истинности будет иметь 2⁶ = 64 строк (т.к. 6 переменных).
4 из них нам известны: в них x3 два раза не совпадает с F.
Неизвестных строк:

 
64 - 4 = 60

В неизвестных x3 может не совпадать с F, кроме того, в двух известных x3 не совпадает с F. Соответственно максимально возможное число строк с несовпадающими x3 и F, будет:

60 + 2 = 62

Результат: 62

Задание 2_9: Решение 2 задания ЕГЭ по информатике:

Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	x6	x7	F
			0		0		0
			0			0	1
1			1				1

Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7

✍ Решение:

Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).

1 пункт:

(((x1 ∧ (x2 → x3) ∧  ¬x4) ∧ x5) ∧ x6)  ∧ ¬x7

Внешняя операция — конъюнкция. Ее проще проверять по строке, в которой F = 1 (значит все сомножители должны быть равны 1).
Возьмем 3-ю строку, в ней x4=1. В нашем выражении х4 с отрицанием, т.е. = 0. Для конъюнкции, когда хоть один из сомножителей равен нулю, выражение вернет в результате 0, а у нас в строке 1. Т.е. этот пункт не подходит:

2 пункт:

(((x1 ∨ (¬x2 → x3) ∨  ¬x4) ∨ ¬x5) ∨ x6)  ∨ ¬x7

Последняя выполняющаяся операция (внешняя) — дизъюнкция. Ее легче проверять по строке, в которой F = 0 (значит все слагаемые должны быть равны 0).
Смотрим по первой строке: х4 = 0, в рассматриваемом пункте он с отрицанием, т.е. = 1. Соответственно все выражение вернет единицу, а в таблице в строке 0. Т.е. этот пункт не подходит:

3 пункт:

(((¬x1 ∧ (x2 → ¬x3) ∧  x4) ∧ ¬x5) ∧ x6) ∧ x7

Последняя операция — конъюнкция. Ее проще проверять по строке, в которой F = 1 (значит все сомножители должны быть равны 1).
Возьмем 2-ю строку: в ней х7 = 0, в рассматриваем пункте х7 без отрицания, т.е. так и остается равным нулю. При умножении выражение вернет в результате 0. В таблице — 1. Т.е. пункт тоже не подходит:

Единственным подходящим вариантом остался пункт под номером 4 (на всякий случай всегда стоит проверить и его).

Результат: 4

В видеоуроке рассмотрено подробное решение 2 задания:

📹 здесь

Задание 2_1: Задание 2 ЕГЭ по информатике:

Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

№	Перем. 1	Перем. 2	Перем. 3	F
	???	???	???	F
1	0	0	0	0
2	0	0	1	0
3	0	1	0	1
4	0	1	1	1
5	1	0	0	0
6	1	0	1	0
7	1	1	0	0
8	1	1	1	1

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:

(y → x) ∧ (y → z) ∧ z

Конъюнкцию легче рассматривать по тем строкам таб. ист-ти, в которых F = 1, т.е. №3, №4, и №8
Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная z тоже была истинной (=1)

(y → x) ∧ (y → z) ∧ z = 1
   если: 
1. (y → x) = 1
2. (y → z) = 1
3. z = 1

Поскольку с выражениями в скобках сложней работать, определим сначала какому столбцу соответствует z. Для этого выберем строку (№3), где F = 1, а в остальных ячейках только одна единица, остальные — нули.

№	Перем. 1	Перем. 2	Перем. 3	F
3	0	1	0	1

Таким образом, делаем вывод, что z находится во втором столбце (отсчет ведем слева):

№	Перем. 1	Перем. 2	Перем. 3	F
_	???	z	???	F

Дальше нам необходимо рассмотреть две скобки, в которых находится операция импликации: (y → x) и (y → z). Обе эти скобки должны возвращать истину (=1). В таб. истинности для импликации, функция возвращает в результате 1 тогда, когда:
вторая переменная (заключение) равна 1 (первая при этом может быть любой),
вторая переменная (заключение) равна 0, а первая обязательно должна быть равна тоже 0.
Рассмотрим скобку (y → x) и строку 4 таблицы:

№	Перем. 1	z	Перем. 3	F
4	0	1	1	1

Для этой строки только y может быть равен 0, т.к. если x = 0, тогда y=1, и скобка в результате возвратит ложь (1 → 0 = 0). Соответственно, y находится в первом столбце. А x значит должен стоять в третьем:

Результат: yzx

Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:

📹 здесь

Источник

Две трети выпускников проваливают 18 задание ЕГЭ по информатике. Как же его решать? Нужно знать особый подход. Давайте разберемся, как эффективно справиться с этим коварным заданием.

В ЕГЭ по информатике есть четыре задания на математическую логику. Сегодня речь пойдёт о задании №18, которое связано с анализом логического высказывания. Статистика ужасна: по оценке ФИПИ с ним справляются чуть меньше 1/3 сдающих. Почему 18 задание ЕГЭ по информатике вызывает сложности? Давайте разберемся, что надо знать, понимать и уметь, чтобы их избежать.

А если вас интересуют и другие задания, эффективно подготовиться к ЕГЭ по информатике можно на наших курсах.

Вам нужны знания не только математической логики, но и просто математики. В качестве логической переменной (которая может быть истина или ложна) выступают не просто некие x, y, z, а математические высказывания. В ответе надо определить значения некоторого параметра, зависящего от этих переменных. Что-то напоминает? Да, почти как в задании 18 из профильной математики, но тут будет намного проще. Например, логической переменной может выступать выражение «x>10» или суждение о том, что x кратен 5. Рассмотрим, как подходить к такому виду логической переменной.

Если логическая переменная — неравенство

Все просто. Выражение «x>10» истинно для всех х, которые являются решением данного неравенства, то есть для x от 10 до +∞. И это выражение ложно для всех x, которые можно описать неравенством (x≤10) или x∈(+∞; 10]. Обратите внимание на число 10, когда x=10, логическая переменная (x>10) ложна.

Если логическая переменная — утверждение

Допустим, наша переменная — «x делится на 5». Тогда она истинна для всех х, которые кратны 5 (0, 5, 10, 15,…). Обратите внимание на то, что 0 кратен любому числу, а значит кратен 5 и тоже даст истинное значение. Методом исключения, данная логическая переменная ложна при всех х, которые не делятся на 5.

Вторая сложность в 18 задании ЕГЭ по информатике

Когда такие переменные рассматриваются отдельно, все выглядит просто. Но в 18 задании у вас будет целое логическое высказывание, содержащее несколько переменных и параметр, значение которого вам надо определить.

Это и есть вторая сложность данного задания — надо знать, как правильно подходить к анализу выражения. Для этого нужно помнить о двух принципиальных шагах:

Упрости, если есть возможность.
Определи «красную зону»

18 задание ЕГЭ по информатике важно решать постепенно. Сначала поговорим об упрощении, так как без этого шага очень сложно начать анализ. Затем обсудим, что такое «красная зона».

Как упростить выражение?

Смысл
этого шага в двух моментах:

Введите обозначения для удобства записи. Иначе некоторые переменные получаются слишком громоздкими.
Упростите зависимости логических переменных. Выражение, где смешаны несколько уровней скобок и логических функций, сложно анализировать. А вот идентичное ему выражение, в котором три переменных связаны дизъюнкцией, намного проще.

Для большинства заданий вам нужно знать несколько формул матлогики. Сохраните эту картинку, пригодится.

Формулы упрощения — 18 задание ЕГЭ по информатике

Что такое «красная зона»?

В задании нужно определить значения параметра, чтобы логическое высказывание было тождественно истинно при любых значениях переменной x. При этом мы не можем брать произвольно большой набор значений для искомого параметра, это также определяется условием задания. Поэтому нужно подбирать такие значения параметра, чтобы они закрывали только определённый ряд случаев, не больше и не меньше. Этот ряд случаев назовем «красной зоной», теми значениями переменной x, когда логическое высказывание не будет истинно при любых значениях параметра.

Простой пример. Возьмем логическое высказывание: (X < 50) V (X > A).

Нам не важно значение параметра А. У нас есть одно логическое слагаемое, которое истинно. Второе может быть ложно — дизъюнкция все равно в итоге даст истину. Значит «красная зона» — это все х≥50. Подбирать значение для параметра А необходимо только для случаев, когда х≥50, чтобы за счет второго слагаемого (где содержится А) обеспечить истинность всего выражения, когда первая скобка ложна.

Для правильного анализа красной зоны важно помнить об основных
моментах анализа некоторых логических функций:

Конъюнкция нескольких переменных будет истинна, только если каждый множитель истинен, и ложна, если хотя бы один множитель ложен.
Дизъюнкция нескольких переменных будет истинна, если хотя бы одно слагаемое истинно, и ложна, только если ложны все слагаемые.
Импликация ложна только в единственном случае — когда из истины следует ложь.

Примеры 18 задания ЕГЭ по информатике

Рассмотрим правильный подход на различных прототипах данного задания.

Пример 1

Решение

В данном логическом высказывании не требуется упрощений, так как у нас простой для анализа случай: дизъюнкция трёх переменных. Поэтому перейдём сразу к анализу и определению «красной зоны».

Вторая и третья скобки не зависят от А и обеспечат истинность всего выражения, независимо от параметра, если X>15 или Y>30. Тогда красной зоной будет ситуация, когда не выполняются ОБА из этих условий, то есть и вторая, и третья скобки одновременно ложны. Опишем этот случай системой:

В этой ситуации нам необходимо обеспечить истинность первой скобки, которая зависит от параметра. Дополним систему ещё одним условием.

Теперь мы свели задание к решению системы простейших неравенств. Определим границы для параметра А при помощи работы с неравенствами. Первое неравенство умножим на 2, затем сложим новое неравенство со вторым и сведём это всё к одному двойному неравенству за счёт одинакового выражения Y+2X.

Осталось вернуться к формулировке вопроса. Вас всегда будут спрашивать что-то конкретное относительно значений параметра А! В данном случае нам надо найти наименьшее целое значение. В случае A > 60 наименьшим подходящим целым значением будет 61. Внимание! Всегда отслеживайте строгость и нестрогость знаков, значение 60 не подходит под условие A > 60, так как 60 равно 60, но не как не больше.

Ответ:

Пример 2

Здесь необходимо начать с упрощения выражения. Введём обозначения для краткости и удобства записи.

Выражение сразу выглядит намного проще.

Теперь применим формулу для раскрытия импликации на базовые функции.

Далее воспользуемся формулой де Моргана.

Уберём двойное отрицание и лишние скобки.

И финальным шагом уберём тавтологию.

Сравните с тем, что было в условии. Стало проще, правда? Дальше мы будем анализировать именно это выражение.

«Красная зона» будет также определяться из случая, когда дизъюнкция будет истинна не из-за переменных, которые не зависят от А, а исключительно из-за переменной с параметром. Получается, для этого первое и второе слагаемые должны быть ложны. Получаем, что P = 1 и Q = 1, в таком случае и A = 1. Теперь вернёмся от наших обозначений к исходным описаниям переменных.

Значит наша «красная зона» — это пересечение отрезков P и Q. Чтобы покрыть ровно эту часть числовой прямой, отрезок А должен ровняться пересечению отрезков P и Q.

Получаем: A = [150; 171].

В ответ надо указать минимально возможную длину отрезка. Мы подбирали значение отрезка А так, чтобы сразу закрыть им только необходимое и не больше, поэтому полученный отрезок и есть отрезок минимальной длинны.

Длина отрезка считается очень просто: из большей границы вычитается меньшая. Длина отрезка А = 171 – 150 = 21.

Ответ: 21

Пример 3

Решение

В данном примере тоже нужно упростить выражение. Введём обозначения:

Получаем выражение

Дальше потребуется только раскрыть импликации, убрать двойное отрицание и лишние скобки.

Теперь переходим к определению «красной зоны». Когда D6=1 и D4 = 1, то и DA должно быть истинно.

Вернемся к математическому смыслу наших переменных. Получаем условие: числа, которые кратны 4 и 6 одновременно, должны быть кратны и А. Пользуясь понятием наименьшего общего кратного (НОК) из математики, получаем, что числа, которые одновременно кратны 4 и 6 – это числа, кратные 12.

Переформулируем условие: числа, которые кратны 12, должны быть кратны А. Отсюда уже понятно, что А = 12. Если мы возьмём число меньшее, например 2, выражение будет истинно, но это не максимальное возможное значение, которое просят по условию. А если возьмём число больше, например 24, для x=12 выражение окажется ложным. Кратность 4 и 6 будет обнулять второе и третье слагаемое, а первое окажется ложно, так как 12 не кратно 24, а наоборот 24 кратно 12.

Ответ:
12

Пример 4

Решение

В этом примере встречается поразрядная конъюнкция. Суть этого вычислительного действия проста: мы выполняем логическое умножение чисел, записанных двоичным кодом, по разрядам (нулевой с нулевым, первый с первым и т.д.). Подробнее на поразрядную конъюнкцию взглянем уже при анализе выражения. Для начала упростим то, что надо анализировать. Введём обозначения:

Получим выражение

Дальше потребуется только раскрыть импликацию и убрать лишние скобки

Теперь переходим к определению «красной зоны». Она возникает, когда Z39 = 0 и Z41 = 1, и ZA должно быть ложно.

Переходим
обратно к математическому смыслу наших переменных. Запишем условия следующим
образом: для х, для которых поразрядная конъюнкция с 41 даёт 0, а с 39 даёт не
0, поразрядная конъюнкция с А должна давать не 0.

Определим, что такое х из «красной зоны».

Посмотрим
на первое условие: поразрядная конъюнкция с 41 даёт 0. Чтобы посчитать
поразрядную конъюнкцию переводим 41 в двоичную систему счисления и получаем
101001₂.

Чтобы в итоге поразрядной конъюнкции получился ноль, в тех разрядах, где в числе 41 стоят единицы, у числа х должны обязательно стоять нули. Там же, где в числе 41 стоят нули – в числе х может быть всё что угодно, так как одного нуля для обнуления произведения достаточно. Изобразим это схематически.

Мы получили некоторый «макет» чисел «красной зоны». Но он пока не полный. Переходим ко второму условию: поразрядная конъюнкция с 39 даёт не 0. Также необходимо перевести число в двоичную систему счисления. 39₁₀ = 100111₂. Чтобы в итоге поразрядной конъюнкции получить не 0, хотя бы один из разрядов, где у 39 стоят единицы, в х тоже должен содержать единицу. Достаточно одной, но она может быть на любом из доступных мест (кроме, тех, где из-за анализа первого условия мы уже поставили 0).

Теперь у нас есть полная схема чисел, которые представляют собой «красную зону». У таких чисел в нулевом, третьем, пятом разряде точно стоят нули, а в первом или во втором (или и в том и том) стоят единицы.

Теперь, чтобы определить наименьшее значение параметра А, при котором выражение будет тождественно истинно, надо обеспечить, чтобы при минимальном количестве единиц в разрядах (минимальном, но не меньше чем необходимо) можно было обеспечить ненулевое значение поразрядной конъюнкции иксов из «красной зоны» с числом А. Для этого нам обязательно надо закрыть единицами первый и второй разряды (тогда хотя бы в одном из этих разрядов точно получится 1), а остальные можно спокойно занять нулями.

Последнее, что осталось сделать — перевести число А в десятичную систему счисления. 110₂ = 6₁₀.

Ответ: 6

Подведем итоги

Теперь вы умеете решать 18 задание ЕГЭ по информатике. Такой подход с упрощением выражения и постепенным анализом позволяет разбить длительную работу с заданием на небольшие этапы. Вы постепенно составляете выводы о том, каким же должен быть параметр в этом задании.

Остается закрепить знания на практике. Напомню, что эффективно подготовиться к ЕГЭ по информатике можно на наших курсах. Используйте промокод BLOG0320 до 31 марта 2020 года включительно и получите первый месяц онлайн-подготовки со скидкой 50%.

Источник