Диагностические и тренировочные варианты СтатГрад ЕГЭ Профиль по математике с ответами
Расписание СтатГрад 11 класс ЕГЭ 2022
22.09.2016
10109-22.09.2016
10110-22.09.2016
10111-22.09.2016
10112-22.09.2016
20.12.2016
10209-20.12.2016
10210-20.12.2016
10211-20.12.2016
10212-20.12.2016
26.01.2017
10309-26.01.2017
10310-26.01.2017
10311-26.01.2017
10312-26.01.2017
06.03.2017
10609-06.03.2017
10610-06.03.2017
10611-06.03.2017
10612-06.03.2017
21.04.2017
10709-21.04.2017
10710-21.04.2017
10711-21.04.2017
10712-21.04.2017
21.09.2017
10109-21.09.2017
10110-21.09.2017
10111-21.09.2017
10112-21.09.2017
21.12.2017
10209-21.12.2017
10210-21.12.2017
10211-21.12.2017
10212-21.12.2017
25.01.2018
10309-25.01.2018
10310-25.01.2018
10311-25.01.2018
10312-25.01.2018
06.03.2018
10409-06.03.2018
10410-06.03.2018
10411-06.03.2018
10412-06.03.2018
18.04.2018
10509-18.04.2018
10510-18.04.2018
10511-18.04.2018
10512-18.04.2018
20.09.2018
10109-20.09.2018
10110-20.09.2018
10111-20.09.2018
10112-20.09.2018
20.12.2018
10209-20.12.2018
10210-20.12.2018
10211-20.12.2018
10212-20.12.2018
24.01.2019
10309-24.01.2019
10310-24.01.2019
10311-24.01.2019
10312-24.01.2019
06.02.2019 (10 класс)
00309-06.02.2019
00310-06.02.2019
13.03.2019
10409-13.03.2019
10410-13.03.2019
10411-13.03.2019
10412-13.03.2019
19.04.2019
10509-19.04.2019
10510-19.04.2019
10511-19.04.2019
10512-19.04.2019
24.04.2019 (Итоговая контрольная работа Профильный уровень 10 класс)
00403-24.04.2019
00404-24.04.2019
17.05.2019 (10-11 класс)
00509-17.05.2019
00510-17.05.2019
00511-17.05.2019
00512-17.05.2019
25.09.2019
1910109-25.09.2019
1910110-25.09.2019
1910111-25.09.2019
1910112-25.09.2019
18.12.2019
1910209-18.12.2019
1910210-18.12.2019
1910211-18.12.2019
1910212-18.12.2019
29.01.2020
1910309-29.01.2020
1910310-29.01.2020
1910311-29.01.2020
1910312-29.01.2020
06.02.2020 (10 класс)
1900209-06.02.2020
1900210-06.02.2020
12.02.2020 (10 класс Тригонометрия)
1900403-12.02.2020
1900404-12.02.2020
11.03.2020
1910409-11.03.2020
1910410-11.03.2020
1910411-11.03.2020
1910412-11.03.2020
02.04.2020 (10 класс Теория вероятностей и статистика)
1900503-02.04.2020
1900504-02.04.2020
15.04.2020 (10 класс Итоговая уровневая работа)
1900603-15.04.2020
1900604-15.04.2020
22.04.2020
1910509-22.04.2020
1910510-22.04.2020
1910511-22.04.2020
1910512-22.04.2020
15.05.2020
1900709-15.05.2020
1900710-15.05.2020
30.09.2020
2010109-30.09.2020
2010110-30.09.2020
2010111-30.09.2020
2010112-30.09.2020
16.12.2020
2010209-16.12.2020
2010210-16.12.2020
2010211-16.12.2020
2010212-16.12.2020
28.01.2021 (10 класс)
2000309-28.01.2021
2000310-28.01.2021
10.02.2021
2010309-10.02.2021 [с видео-разбором]
2010310-10.02.2021
2010311-10.02.2021
2010312-10.02.2021
16.03.2021
2010409-16.03.2021
2010410-16.03.2021
2010411-16.03.2021
2010412-16.03.2021
29.04.2021
2010509-29.04.2021 [с видео-разбором]
2010510-29.04.2021
2010511-29.04.2021
2010512-29.04.2021
13.05.2021
2000709-13.05.2021
2000710-13.05.2021
28.09.2021
2110109-28.09.2021
2110110-28.09.2021
2110111-28.09.2021
2110112-28.09.2021
15.12.2021
2110209-15.12.2021
2110210-15.12.2021
2110211-15.12.2021
2110212-15.12.2021
27.01.2022 (10-11 класс)
2100109-27.01.2022
2100110-27.01.2022
16.02.2022
2110309-16.02.2022
2110310-16.02.2022
2110311-16.02.2022
2110312-16.02.2022
15.03.2022
2110409-15.03.2022
2110410-15.03.2022
2110411-15.03.2022
2110412-15.03.2022
28.04.2022
2110509-28.04.2022
2110510-28.04.2022
2110511-28.04.2022
2110512-28.04.2022
18.05.2022
2100309-18.05.2022
2100310-18.05.2022
28.09.2022
2210109-28.09.2022
2210110-28.09.2022
2210111-28.09.2022
2210112-28.09.2022
13.12.2022
2210209-13.12.2022
2210210-13.12.2022
2210211-13.12.2022
2210212-13.12.2022
08.02.2023 (10 класс)
2200109-08.02.2023
2200110-08.02.2023
28.02.2023
2210309-28.02.2023
2210310-28.02.2023
2210311-28.02.2023
2210312-28.02.2023
Тренировочная работа №2 пробный ЕГЭ 2022 статград по математике 11 класс составлена по образцу экзамена ЕГЭ 2022 года , тренировочные варианты с МА2110201 по МА2110212 базового и профильного уровня с ответами на тестовую часть и решением на 2 часть заданий официальная дата проведения работы 15 декабря 2021 год.
-
Варианты базового уровня
-
Варианты профильного уровня
-
Ответы, решения и критерии
Решать тренировочные варианты базового уровня статград ЕГЭ 2022 по математике 11 класс:
Решать тренировочные варианты профильного уровня статград ЕГЭ 2022 по математике 11 класс:
Сложные задания с МА2110201 варианта:
2)Установка двух счётчиков воды (холодной и горячей) стоит 3500 рублей. До установки счётчиков за воду платили 1100 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 900 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
3)Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
4)Результаты соревнований по метанию молота представлены в таблице. Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Какое место занял спортсмен Минаков?
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)Магазин детских товаров закупает погремушки по оптовой цене 110 рублей за одну штуку и продаёт с наценкой 30 %. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?
10)Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 8:00?
11)На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,25. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
12)На соревнованиях по прыжкам в воду судьи выставили оценки от 0 до 10 трём спортсменам. Результаты приведены в таблице. Итоговый балл вычисляется следующим образом: две наибольшие и две наименьшие оценки отбрасываются, а три оставшиеся складываются, и их сумма умножается на коэффициент сложности. В ответе укажите номера спортсменов, итоговый балл которых больше 170, без пробелов, запятых и других дополнительных символов.
13)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй коробки больше объёма первой?
16)Сторона основания правильной шестиугольной пирамиды равна 22, боковое ребро равно 61. Найдите площадь боковой поверхности этой пирамиды.
18)Некоторые учащиеся школы съели за завтраком булочку с рисом. Некоторые учащиеся этой школы на обед получат пирожок, причём среди них не будет тех, кто съел за завтраком булочку. Выберите все утверждения, которые будут верны при указанных условиях независимо от того, кому достанутся пирожки. 1) Нет ни одного учащегося этой школы, который съел булочку за завтраком и получит пирожок на обед. 2) Найдётся учащийся, который не съел булочку за завтраком и не получит пирожок на обед. 3) Каждый учащийся, который не съел булочку за завтраком, получит пирожок на обед. 4) Среди учащихся этой школы, которым не достанется пирожок на обед, есть хотя бы один, который съел булочку за завтраком. В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19)Найдите четырёхзначное число, кратное 24, произведение цифр которого равно 16. В ответе запишите запишите какое-нибудь одно такое число.
20)Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 5,5 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
21)Улитка за день заползает вверх по дереву на 3 м, а за ночь сползает на 1 м. Высота дерева равна 13 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Сложные задания с МА2110205 варианта:
2)В квартире установлен прибор учёта расхода горячей воды (счётчик). Показания счётчика 1 июля составляли 77,2 куб. м воды, а 1 августа — 79,7 куб. м. Сколько нужно заплатить за горячую воду за июль, если стоимость 1 куб. м горячей воды составляет 144 руб. 80 коп.? Ответ дайте в рублях.
3)Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
4)Результаты игры КВН представлены в таблице. Для каждой команды баллы по всем конкурсам суммируются. Победителем считается команда, набравшая в сумме наибольшее количество баллов. Сколько в сумме баллов у команды-победителя?
6)Тетрадь стоит 18 рублей. Сколько рублей заплатит покупатель за 30 тетрадей, если при покупке более 20 тетрадей магазин делает скидку 5 % от стоимости всей покупки?
10)Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
11)На борту самолёта 27 мест рядом с запасными выходами и 17 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир З. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру З. достанется удобное место, если всего в самолёте 400 мест.
12)В трёх салонах сотовой связи один и тот же смартфон продаётся в кредит на разных условиях. Условия приведены в таблице. Определите, в каком из салонов покупка обойдётся дешевле всего (с учётом переплаты). В ответе запишите стоимость этой покупки в рублях.
13)Вода в сосуде, имеющем форму правильной четырёхугольной призмы, находится на уровне h = 120 см. На каком уровне окажется вода, если её перелить в другой сосуд, имеющий форму правильной четырёхугольной призмы, у которого сторона основания вдвое больше, чем у данного? Ответ дайте в сантиметрах.
16)Сторона основания правильной шестиугольной пирамиды равна 14, боковое ребро равно 25. Найдите площадь боковой поверхности этой пирамиды.
18)Некоторые учащиеся 10-х классов школы зимой ездили на экскурсию в Суздаль. Весной некоторые десятиклассники поедут в Кострому, причём среди них не будет тех, кто ездил зимой в Суздаль. Выберите все утверждения, которые будут верны при указанных условиях независимо от того, кто из десятиклассников поедет в Кострому. 1) Среди учащихся 10-х классов этой школы, которые не поедут в Кострому, есть хотя бы один, который ездил на экскурсию в Суздаль. 2) Найдётся десятиклассник, который не ездил на экскурсию в Суздаль и не поедет в Кострому. 3) Нет ни одного десятиклассника, который ездил на экскурсию в Суздаль и поедет в Кострому. 4) Каждый десятиклассник, который не был на экскурсии в Суздале, поедет в Кострому.
19)Найдите четырёхзначное число, кратное 12, произведение цифр которого больше 25, но меньше 30. В ответе запишите какое-нибудь одно такое число.
20)Толя и Саша выполняют одинаковый тест. Толя отвечает за час на 12 вопросов теста, а Саша — на 17. Они одновременно начали отвечать на вопросы теста, и Толя закончил свой тест позже Саши на 50 минут. Сколько вопросов содержит тест?
21)Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив 8 прыжков?
Сложные задания с МА2110209 варианта:
2)В классе 9 учащихся, среди них два друга — Олег и Сергей. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Олег и Сергей окажутся в одной группе.
3)Боковые стороны равнобедренного треугольника равны 13, основание равно 24. Найдите радиус описанной около этого треугольника окружности.
5)В правильной четырёхугольной пирамиде все рёбра равны 22. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
8)Два человека отправляются одновременно из одного дома на прогулку до опушки леса, находящейся в 6,3 км от дома. Первый идёт со скоростью 2,5 км/ч, а второй — со скоростью 3,8 км/ч. Дойдя до опушки, второй разворачивается и с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
10)На фабрике керамической посуды 20 % произведённых тарелок имеют дефект. При контроле качества продукции выявляется 90 % дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефекта. Ответ округлите до сотых.
13)В правильной шестиугольной пирамиде SABCDEF с вершиной S в грани SBC проведена высота SH , а в грани SEF проведена высота SK. а) Докажите, что прямая AD перпендикулярна плоскости SHK. б) Найдите угол между прямыми BE и SH , если SA =13, а BC =10 .
15)В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг будет возрастать на 14 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна сумма всех платежей после полного погашения кредита, если наименьший годовой платёж будет составлять 475 000 рублей?
16)Диагонали АС и ВD выпуклого четырёхугольника ABCD пересекаются в точке Р . Известно, что угол DAC равен 90° , а угол ACB в 2 раза больше угла ADB. Сумма угла DBС и удвоенного угла ADС равна 180 . ° а) Докажите, что ВР АР = 2 . б) Найдите площадь четырёхугольника AВCD , если BD = 8 и точка Р является серединой диагонали BD .
Сложные задания с МА2110211 варианта:
2)В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист К. полетит пятым рейсом вертолёта.
3)Периметр прямоугольной трапеции, описанной около окружности, равен 36, её бóльшая боковая сторона равна 11. Найдите радиус окружности.
5)Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны 14, а высота равна 24.
8)Феде надо решить 133 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днём. Известно, что за первый день Федя решил 7 задач. Определите, сколько задач решил Федя в последний день, если со всеми задачами он справился за 7 дней.
10)Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,4. Найдите вероятность того, что в течение года в фонаре хотя бы одна лампа не перегорит.
13)В правильной шестиугольной пирамиде SABCDEF с вершиной S в грани SBC проведена высота SH , а в грани SEF проведена высота SK. а) Докажите, что прямая AD перпендикулярна плоскости SHK. б) Найдите угол между прямыми BE и SH , если SA =13, а BC =10 .
15)В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг будет возрастать на 14 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна сумма всех платежей после полного погашения кредита, если наименьший годовой платёж будет составлять 475 000 рублей?
16)Диагонали АС и ВD выпуклого четырёхугольника ABCD пересекаются в точке Р . Известно, что угол DAC равен 90° , а угол ACB в 2 раза больше угла ADB. Сумма угла DBС и удвоенного угла ADС равна 180 . ° а) Докажите, что ВР АР = 2 . б) Найдите площадь четырёхугольника AВCD , если BD = 8 и точка Р является серединой диагонали BD .
Другие тренировочные варианты ЕГЭ 2022 по математике 11 класс:
-
Математика 11 класс ЕГЭ 2022 профиль 3 варианта контрольной работы
-
Пробный вариант №211206 ЕГЭ 2022 по математике профиль 11 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тренировочная работа №5 статград ЕГЭ 2022 по математике 11 класс задания и ответы для тренировочных вариантов МА2110501-МА2110512 базового и профильного уровня. Официальная дата проведения работы: 28 апреля 2022 год.
Скачать варианты базового уровня
Скачать варианты профильного уровня
Все ответы (решения) и задания (без водяного знака)
Тренировочные варианты статград математика 11 класс ЕГЭ 2022 профильный уровень МА2110509-МА2110512
Тренировочные варианты статград математика 11 класс ЕГЭ 2022 базовый уровень МА2110501-МА2110508
Задания и ответы варианта МА2110501 статграда:
2)Мотоциклист проехал 14 километров за 21 минуту. Сколько километров он проедет за 30 минут, если будет ехать с той же скоростью?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку значение атмосферного давления в среду в 6:00. Ответ дайте в миллиметрах ртутного столба.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)В период распродажи магазин снижал цены дважды: в первый раз на 10 %, во второй — на 25 %. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?
10)Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота перил h1 равна 1 м, а наибольшая высота h2 равна 2 м. Ответ дайте в метрах.
11)В фирме такси в наличии 20 легковых автомобилей: 7 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
13)Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
15)В треугольнике ABC проведена биссектриса AL, угол ALC равен 160° , угол ABC равен 148° . Найдите угол ACB . Ответ дайте в градусах.
18)Во дворе школы растут всего три дерева: берёза, клён и дуб. Берёза выше клёна на 1 метр, но ниже дуба на 3 метра. Выберите утверждения, которые верны при указанных условиях. 1) Среди указанных деревьев не найдётся двух одной высоты. 2) Берёза, растущая во дворе школы, выше дуба, растущего там же. 3) Любое дерево, помимо указанных, которое ниже берёзы, растущей во дворе школы, также ниже клёна, растущего там же. 4) Любое дерево, помимо указанных, которое ниже клёна, растущего во дворе школы, также ниже берёзы, растущей там же.
19)Найдите четырёхзначное число, большее 1000, но меньшее 1700, которое делится на 45 и сумма цифр которого равна 18. В ответе укажите какое-нибудь одно такое число.
20)Теплоход, скорость которого в неподвижной воде равна 24 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 4 км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 36 часов после отправления из него. Сколько километров проходит теплоход за весь рейс?
21)Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 254, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Задания и ответы варианта МА2110502 статграда:
2)За 20 минут автобус проехал 23 километра. Сколько километров он проедет за 35 минут, если будет ехать с той же скоростью?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку значение атмосферного давления в четверг в 12:00. Ответ дайте в миллиметрах ртутного столба.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)В период распродажи магазин снижал цены дважды: в первый раз на 15 %, во второй — на 25 %. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 2000 рублей?
10)Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота перил h1 равна 0,7 м, а наибольшая высота h2 равна 1,5 м. Ответ дайте в метрах.
11)В фирме такси в наличии 15 легковых автомобилей: 3 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
13)Однородный шар диаметром 3 см весит 189 грамм. Сколько граммов весит шар диаметром 4 см, изготовленный из того же материала?
15)В треугольнике ABC проведена биссектриса AL, угол ALC равен 41° , угол ABC равен 26° . Найдите угол ACB . Ответ дайте в градусах.
18)Кошка Китти весит на 3 килограмма больше кошки Машки, а кошка Лада на полтора килограмма легче кошки Машки. Выберите утверждения, которые верны при указанных условиях. 1) Любая кошка, помимо указанных, которая весит меньше Лады, весит также меньше Китти. 2) Любая кошка, помимо указанных, которая весит меньше Китти, весит также меньше Лады. 3) Среди указанных кошек нет кошек тяжелее Китти. 4) Машка весит меньше Лады.
19)Найдите четырёхзначное число, большее 1500, но меньшее 2000, которое делится на 24 и сумма цифр которого равна 21. В ответе укажите какоенибудь одно такое число.
20)Теплоход, скорость которого в неподвижной воде равна 15 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 7 часов, а в исходный пункт теплоход возвращается через 37 часов после отправления из него. Сколько километров проходит теплоход за весь рейс?
21)Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 496, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Задания и ответы варианта МА2110505 статграда:
2)Принтер печатает одну страницу за 8 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 14 минут?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления (в миллиметрах ртутного столба) в четверг.
6)Банк начисляет на срочный вклад 8 % годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?
10)Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки h равна 3,9 м. Ответ дайте в метрах.
11)На экзамене будет 50 билетов, Серёжа не выучил 11 из них. Найдите вероятность того, что ему попадётся выученный билет.
13)Две кружки имеют форму цилиндра. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём первой кружки меньше объёма второй?
14)На рисунке точками показан годовой объём добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали — объём добычи угля в миллионах тонн. Для наглядности точки соединены ломаной линией.
16)В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 3 и 16. Найдите объём призмы, если её высота равна 3.
18)Двадцать выпускников одного из одиннадцатых классов сдавали ЕГЭ по русскому языку. Самый низкий балл, полученный в этом классе, был равен 28, а самый высокий — 83. Выберите утверждения, которые верны при указанных условиях. 1) Среди этих выпускников есть человек, который получил 83 балла за ЕГЭ по русскому языку. 2) Среди этих выпускников есть двадцать человек с равными баллами за ЕГЭ по русскому языку. 3) Среди этих выпускников есть человек, получивший 100 баллов за ЕГЭ по русскому языку. 4) Баллы за ЕГЭ по русскому языку любого из этих двадцати человек не ниже 27.
19)Найдите четырёхзначное число, большее 2000, но меньшее 4000, которое делится на 18 и каждая следующая цифра которого больше предыдущей. В ответе укажите какое-нибудь одно такое число.
20)Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 19 км. Путь из А в В занял у туриста 5 часов, из которых 4 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
21)Список заданий викторины состоял из 50 вопросов. За каждый правильный ответ ученик получал 9 очков, за неправильный ответ с него списывали 16 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 171 очко, если известно, что по крайней мере один раз он ошибся?
Задания и ответы варианта МА2110506 статграда:
2)Принтер печатает одну страницу за 9 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 12 минут?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления (в миллиметрах ртутного столба) во вторник.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)Банк начисляет на срочный вклад 12 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?
10)Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки h равна 3,2 м. Ответ дайте в метрах.
11)На экзамене будет 40 билетов, Яша не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.
13)Даны две кружки цилиндрической формы. Первая кружка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой кружки меньше объёма второй?
14)На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали — прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены ломаной линией.
16)В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 13 и 4. Найдите объём призмы, если её высота равна 5.
18)В посёлке городского типа всего 17 жилых домов. Высота каждого дома меньше 25 метров, но не меньше 5 метров. Выберите утверждения, которые верны при указанных условиях. 1) В посёлке есть жилой дом высотой 25 метров. 2) Разница в высоте любых двух жилых домов посёлка больше 6 метров. 3) В посёлке нет жилого дома высотой 4 метра. 4) Высота любого жилого дома в посёлке не меньше 3 метров.
19)Найдите четырёхзначное число, большее 6000, но меньшее 7000, которое делится на 12 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.2
20)Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 14 км. Путь из А в В занял у туриста 3 часа, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 2 км/ч. Ответ дайте в км/ч.
21)Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 7 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 60 очков, если известно, что по крайней мере один раз он ошибся?
Задания и ответы варианта МА2110509 статграда:
2)В среднем из 75 морозильников, поступивших в продажу, 6 имеют скрытый дефект. Найдите вероятность того, что один случайно выбранный для контроля морозильник не имеет дефекта.
3)В четырёхугольник ABCD , периметр которого равен 56, вписана окружность, AB =12. Найдите длину стороны CD .
5)Шар, объём которого равен 29π , вписан в куб. Найдите объём куба.
8)Из городов A и B одновременно навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 4 часа раньше, чем велосипедист приехал в A, а встретились они через 1 час 30 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
10)По отзывам покупателей Пётр Петрович оценил надёжность двух интернетмагазинов. Вероятность того, что нужный товар доставят из магазина А вовремя, равна 0,84. Вероятность того, что товар доставят вовремя из магазина Б, равна 0,9. Пётр Петрович заказал товары одновременно в двух магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
13)Радиус основания конуса равен 8, высота равна 4. Сечение конуса плоскостью α , проходящей через его вершину, отсекает от окружности основания дугу в 60° . а) Докажите, что величина угла между плоскостью α и плоскостью основания конуса равна 30° . б) Найдите расстояние от центра основания конуса до плоскости сечения.
15)15 августа планируется взять кредит в банке на 16 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 51 % больше, чем сумма, взятая в кредит. Найдите r.
16)Дана равнобедренная трапеция ABCD с основаниями AD и BC , причём AD BC = 2 . а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого. б) Пусть O — точка пересечения диагоналей трапеции. Найдите расстояние от вершины C до середины отрезка OD , если AB =13 и BC =10 .
Задания и ответы варианта МА2110510 статграда:
2)В среднем из 80 морозильников, поступивших в продажу, 4 имеют скрытый дефект. Найдите вероятность того, что один случайно выбранный для контроля морозильник не имеет дефекта.
3)В четырёхугольник ABCD , периметр которого равен 48, вписана окружность, AB =14. Найдите длину стороны CD .
5)Шар, объём которого равен 23π, вписан в куб. Найдите объём куба.
8)Из городов A и B одновременно навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 2 часа раньше, чем велосипедист приехал в A, а встретились они через 1 час 20 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
10)По отзывам покупателей Пётр Петрович оценил надёжность двух интернетмагазинов. Вероятность того, что нужный товар доставят из магазина А вовремя, равна 0,85. Вероятность того, что товар доставят вовремя из магазина Б, равна 0,86. Пётр Петрович заказал товары одновременно в двух магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
13)Радиус основания конуса равен 4, высота равна 6. Сечение конуса плоскостью α , проходящей через его вершину, отсекает от окружности основания дугу в 60° . а) Докажите, что величина угла между плоскостью α и плоскостью основания конуса равна 60° . б) Найдите расстояние от центра основания конуса до плоскости сечения.
15)15 августа планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 38 % больше, чем сумма, взятая в кредит. Найдите r.
16)Дана равнобедренная трапеция ABCD с основаниями AD и BC , причём AD BC = 2 . а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого. б) Пусть O — точка пересечения диагоналей трапеции. Найдите расстояние от вершины C до середины отрезка OD , если AB =17 и BC =16 .
Задания и ответы варианта МА2110511 статграда:
2)Вероятность того, что новому ноутбуку в течение года потребуется ремонт, равна 0,051. Из 1000 проданных ноутбуков в течение года ремонт потребовался 45 ноутбукам. На сколько отличается частота события «в течение года потребуется ремонт» от вероятности этого события?
3)Два угла вписанного в окружность четырёхугольника равны 101° и 99° . Найдите величину большего из оставшихся углов. Ответ дайте в градусах.
5)Один цилиндрический сосуд вчетверо выше второго, зато второй втрое шире первого. Во сколько раз объём второго сосуда больше объёма первого?
8)Имеется два сплава. Первый содержит 10 % никеля, второй — 35 % никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25 % никеля. На сколько килограммов масса первого сплава была меньше массы второго?
10)Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние три промахнулся. Результат округлите до сотых.
15)15 августа планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 56 % больше, чем сумма, взятая в кредит. Найдите r.
16)Дана равнобедренная трапеция ABCD с основаниями AD и BC , причём AD BC = 2 . а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого. б) Пусть O — точка пересечения диагоналей трапеции. Найдите расстояние от вершины C до середины отрезка OD , если AB =15 и BC =18 .
Другие тренировочные варианты статград ЕГЭ по математике 11 класс:
Работы СТАТГРАД по математике задания и ответы
Варианты МА2110401-МА2110412 ЕГЭ 2022 работа статград математика 11 класс с ответами
Share the post «Варианты база и профиль ЕГЭ 2022 работа статград математика 11 класс с ответами»
- VKontakte
Метки: ЕГЭ 2022заданияматематика 11 классответыстатградтренировочная работа
- 20.08.2022
Собираем тренировочные и диагностические работы ЕГЭ от Статграда за 2022-2023 учебный год.
СтатГрад запрещает публиковать их работы (жадины-говядины), поэтому мы публикуем только подробнейшие видеообзоры. Ну а если вам прям хочется порешать сам ким, как реальный вариант ЕГЭ — добро пожаловать в наш раздел «Пробные ЕГЭ 2023», где мы публикуем авторские тренировочные варианты в формате реальных бланком ЕГЭ 2023.
- Всё о ЕГЭ 2023 + что изменилось + демоверсии
- Тренировочные работы ЕГЭ 2023 по всем предметам
- Работы Статград за прошлый год
Ниже представлены даты НА ВЕСЬ учебный год 2022-20213
сентябрь
20.09.2022, вторник, Тренировочная работа №1 по химии 11 класс 2022-2023 гг.
22.09.2022, четверг, Тренировочная работа №1 по русскому языку 11 класс 2022-2023 гг.
28.09.2022, среда, Тренировочная работа №1 по математике 11 класс 2022-2023 гг.
октябрь
04.10.2022, вторник, Тренировочная работа №1 по истории 11 класс 2022-2023 гг.
07.10.2022, пятница, Тренировочная работа №1 по географии 11 класс 2022-2023 гг.
17.10.2022, понедельник, Тренировочная работа №1 по биологии 11 класс 2022-2023 гг.
19.10.2022, среда, Тренировочная работа №1 по обществознанию 11 класс 2022-2023 гг.
20.10.2022, четверг, Тренировочная работа №1 по физике 11 класс 2022-2023 гг.
20.10.2022, четверг, Тематическая тренировочная работа №1 по физике 11 класс 2022-2023 гг.
21.10.2022, пятница, Тематическая тренировочная работа №1 по физике 10 класс 2022-2023 гг.
21.10.2022, пятница, Тренировочная работа №1 по литературе 11 класс 2022-2023 гг.
25.10.2022, вторник, Тренировочная работа №1 по информатике 11 класс 2022-2023 гг.
27.10.2022, четверг, По заявкам. Тренировочная работа №2 по русскому языку 11 класс 2022-2023 гг.
ноябрь
09.11.2022, среда, Тренировочная работа №2 по химии 11 класс 2022-2023 гг.
09.11.2022, среда, По заявкам. Тематическая тренировочная работа №2 по химии 11 класс 2022-2023 гг.
14.11.2022, понедельник, Тренировочная работа №2 по обществознанию 11 класс 2022-2023 гг.
16.11.2022, среда, По заявкам. Диагностическая работа №3 по русскому языку 11 класс 2022-2023 гг.
30.11.2022, среда, Тренировочная работа №1 по английскому языку 11 класс 2022-2023 гг.
декабрь
06.12.2022, вторник, Тренировочная работа №2 по географии 11 класс 2022-2023 гг.
07.12.2022, среда, По заявкам. Диагностическая работа №1 по китайскому языку 11 класс 2022-2023 гг.
09.12.2022, пятница, Тренировочная работа №2 по физике 11 класс 2022-2023 гг.
09.12.2022, пятница, По заявкам. Тематическая тренировочная работа №2 по физике 11 класс 2022-2023 гг.
09.12.2022, пятница, Тематическая тренировочная работа №2 по физике 10 класс 2022-2023 гг.
12.12.2022, понедельник, Тренировочная работа №3 по обществознанию 11 класс 2022-2023 гг.
13.12.2022, вторник, Тренировочная работа №2 по математике 11 класс 2022-2023 гг.
14.12.2022, среда, По заявкам. Тренировочная работа №2 по литературе 11 класс 2022-2023 гг.
15.12.2022, четверг, Тренировочная работа №2 по информатике 11 класс 2022-2023 гг.
15.12.2022, четверг, Тренировочная работа №2 по информатике 11 класс в г. Москве 2022-2023 гг.
20.12.2022, вторник, Тренировочная работа №2 по биологии 11 класс 2022-2023 гг.
22.12.2022, четверг, По заявкам. Тренировочная работа №2 по истории 11 класс 2022-2023 гг.
22.12.2022, четверг, По заявкам. Тематическая тренировочная работа №2 по истории 11 класс 2022-2023 гг.
январь
11.01.2023, среда, Тренировочная работа №3 по химии 11 класс 2022-2023 гг.
17.01.2023, вторник, По заявкам. Тренировочная работа №3 по физике 11 класс 2022-2023 гг.
19.01.2023, четверг, По заявкам. Тренировочная работа №4 по русскому языку 11 класс 2022-2023 гг.
25.01.2023, среда, По заявкам. Тренировочная работа №3 по географии 11 класс 2022-2023 гг.
30.01.2023, понедельник, По заявкам. Диагностическая работа №1 по немецкому языку 11 класс 2022-2023 гг.
30.01.2023, понедельник, По заявкам. Диагностическая работа №1 по французскому языку 11 класс 2022-2023 гг.
30.01.2023, понедельник, По заявкам. Диагностическая работа №1 по испанскому языку 11 класс 2022-2023 гг.
февраль
01.02.2023, среда, Тренировочная работа №4 по обществознанию 11 класс 2022-2023 гг.
03.02.2023, пятница, По заявкам. Тренировочная работа №3 по литературе 11 класс 2022-2023 гг.
06.02.2023, понедельник, Тренировочная работа №3 по химии 11 класс 2022-2023 гг.
07.02.2023, вторник, По заявкам. Диагностическая работа №2 по английскому языку 11 класс 2022-2023 гг.
08.02.2023, среда, Тренировочная работа №1 по математике 10 класс 2022-2023 гг.
09.02.2023, четверг, Тренировочная работа №3 по истории 11 класс 2022-2023 гг.
13.02.2023, понедельник, Тренировочная работа №3 по биологии 11 класс 2022-2023 гг.
14.02.2023, вторник, Тренировочная работа №3 по информатике 11 класс 2022-2023 гг.
16.02.2023, четверг, Диагностическая работа №2 по русскому языку 11 класс 2022-2023 гг.
28.02.2023, вторник, Тренировочная работа №3 по математике 11 класс 2022-2023 гг.
март
02.03.2023, четверг, По заявкам. Тренировочная работа №4 по географии 11 класс 2022-2023 гг.
03.03.2023, пятница, По заявкам. Тренировочная работа №4 по химии 11 класс 2022-2023 гг.
07.03.2023, вторник, Тренировочная работа №4 по физике 11 класс 2022-2023 гг.
09.03.2023, четверг, Тренировочная работа №5 по обществознанию 11 класс 2022-2023 гг.
14.03.2023, вторник, По заявкам. Тренировочная работа №4 по истории 11 класс 2022-2023 гг.
16.03.2023, четверг, По заявкам. Тренировочная работа №6 по русскому языку 11 класс 2022-2023 гг.
17.03.2023, пятница, По заявкам. Тренировочная работа №4 по биологии 11 класс 2022-2023 гг.
28.03.2023, вторник, По заявкам. Тренировочная работа №4 по информатике 11 в г. Москве класс 2022-2023 гг.
28.03.2023, вторник, По заявкам. Тренировочная работа №4 по информатике 11 класс 2022-2023 гг.
30.03.2023, четверг, Тренировочная работа №4 по математике 11 класс 2022-2023 гг.
апрель
04.04.2023, вторник, По заявкам. Тренировочная работа №5 по географии 11 класс 2022-2023 гг.
05.04.2023, среда, По заявкам. Тренировочная работа №3 по английскому языку 11 класс 2022-2023 гг.
06.04.2023, четверг, По заявкам. Тренировочная работа №5 по химии 11 класс 2022-2023 гг.
07.04.2023, пятница, По заявкам. Тренировочная работа №4 по литературе 11 класс 2022-2023 гг.
18.04.2023, вторник, По заявкам. Тренировочная работа №5 по истории 11 класс 2022-2023 гг.
19.04.2023, среда, По заявкам. Тренировочная работа №1 по русскому языку 10-11 класс 2022-2023 гг.
20.04.2023, четверг, По заявкам. Тренировочная работа №5 по физике 11 класс 2022-2023 гг.
21.04.2023, пятница, По заявкам. Тренировочная работа №6 по обществознанию 11 класс 2022-2023 гг.
24.04.2023, понедельник, По заявкам. Тренировочная работа №4 по биологии 11 класс 2022-2023 гг.
25.04.2023, вторник, По заявкам. Тренировочная работа №5 по информатике 11 в г. Москве класс 2022-2023 гг.
25.04.2023, вторник, По заявкам. Тренировочная работа №4 по информатике 11 класс 2022-2023 гг.
27.04.2023, четверг, Тренировочная работа №5 по математике 11 класс 2022-2023 гг.
май
11.05.2023, четверг, Тренировочная работа №2 по математике 10-11 класс 2022-2023 гг.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
14 декабря 2022
В закладки
Обсудить
Жалоба
Решение тестовой части (№1-11) тренировочной работы по математике, 11 класс, вариант МА2210210, от 13 декабря 2022 года.
Тренировочный вариант соответствует демоверсии ЕГЭ-2023.
Задание №1 — 0:31
Задание №2 — 1:58
Задание №3 — 3:15
Задание №4 — 4:39
Задание №5 — 10:34
Задание №6 — 17:27
Задание №7 — 22:36
Задание №8 — 23:23
Задание №9 — 27:07
Задание №10 — 28:57
Задание №11 — 34:15
→ Другие варианты этой работы.
Автор: Matesha Plus — Колесникова Татьяна.
Источник: rutube.ru/channel/23492689/
Решение и ответы заданий варианта 2210109 СтатГрад 28 сентября ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса.


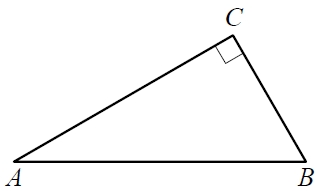
Задание 1.
В треугольнике ABC угол C равен 90°, AB = 4, sinA=frac{sqrt{19}}{10}. Найдите AC.
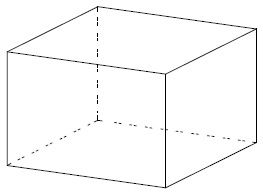
Задание 2.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 4. Объём параллелепипеда равен 140. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Задание 3.
При производстве в среднем из 2000 насосов 4 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Задание 4.
Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».
Задание 5.
Найдите корень уравнения sqrt{frac{7x+13}{19}}=5.
Задание 6.
Найдите значение выражения frac{a^{-1}b^{-1}}{(2a)^{2}b^{-3}}cdot frac{11}{a^{-3}b^{2}}.
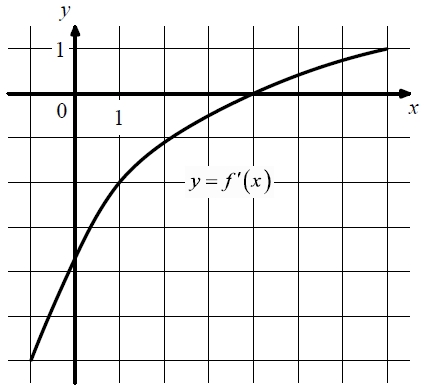
Задание 7.
На рисунке изображён график функции y = f ‘(x) – производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна прямой y = 6 − 2x или совпадает с ней.
Задание 8.
Рейтинг R интернет-магазина вычисляется по формуле , R=r_{пок}–frac{r_{пок}–r_{экс}}{(K+1)^{m}}, где m=frac{0,02K}{r_{пок}+0,1}, rпок – средняя оценка магазина покупателями, rэкс – оценка магазина, данная экспертами, K – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 15, их средняя оценка равна 0,5, а оценка экспертов равна 0,22.
Задание 9.
Расстояние между пристанями A и B равно 60 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 44 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
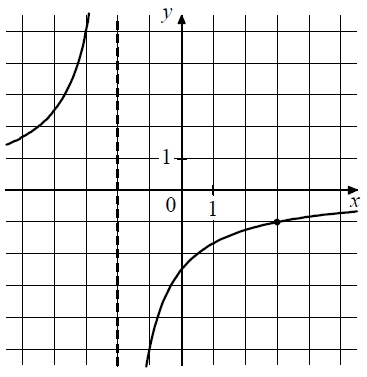
Задание 10.
На рисунке изображён график функции вида f(x)=frac{k}{x+a}. Найдите значение x, при котором f(x) = –0,125.
Задание 11.
Найдите точку минимума функции y = x3 − 6x2 + 15.
Задание 12.
а) Решите уравнение cos2 x − cos2x = 0,75.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{3pi}{2};3pi].
Задание 13.
Ребро куба ABCDA1B1C1D1 равно 2. На ребре BB1 отмечена точка K так, что KB = 1,6. Через точки K и C1 проведена плоскость α , параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 3:1, где P – точка пересечения плоскости α с ребром A1B1.
б) Найдите угол между плоскостями α и BB1C1.
Задание 14.
Решите неравенство frac{(3x–4)^{2}}{x–3}ge frac{16–24x+9x^{2}}{15–8x+x^{2}}.
Задание 15.
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 40 % больше суммы, взятой в кредит. Найдите r.
Задание 16.
Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 9 и AM:MC = 1:8.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
(|x + 2| + |x – a|)2 – 4(|x + 2| + |x – a|) + 3a(4 – 3a) = 0
имеет ровно два решения.
Задание 18.
На сайте проводится опрос, кого из 156 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста – доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно.
а) Всего проголосовало 11 посетителей сайта, и рейтинг первого футболиста стал равен 45. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста?
б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 150 или больше?
в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.2 / 5. Количество оценок: 10
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.