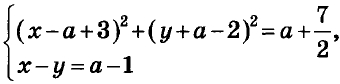При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Найдите значение выражения
Ответ:
2
В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10% от стоимости купленной мебели. Шкаф стоит 3300 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
Ответ:
3
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
А) Объём воды в озере Байкал
Б) Объём пакета кефира
В) Объём бассейна
Г) Объём ящика для фруктов
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 1 л
2) 23 615,39 км3
3) 72 л
4) 600 м3
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
4
На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 3 по 18 сентября 2007 года. По горизонтали указываются числа месяца, по вертикали — цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена олова на момент закрытия торгов была наибольшей за данный период.
Ответ:
5
План местности разбит на клетки. Каждая клетка является квадратом размером 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Ответ:
6
Акции предприятия распределены между государством и частными акционерами в отношении 3 : 5 соответственно. Общая прибыль предприятия после уплаты налогов за год составила 32 млн рублей. Какая сумма из этой прибыли должна пойти на выплату частным акционерам? Ответ дайте в миллионах рублей.
Ответ:
7
Найдите значение выражения
Ответ:
8
9
Найдите корень уравнения
Ответ:
10
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Ответ:
11
На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
Ответ:
12
В магазине одежды объявлена акция: если покупатель приобретает товар на сумму свыше 10 000 руб., он получает сертификат на 1000 рублей, который можно обменять в том же магазине на любой товар ценой не выше 1000 руб. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель И. хочет приобрести пиджак ценой 9500 руб., рубашку ценой 800 руб. и галстук ценой 600 руб. В каком случае И. заплатит за покупку меньше всего:
1) И. купит все три товара сразу.
2) И. купит сначала пиджак и рубашку, галстук получит за сертификат.
3) И. купит сначала пиджак и галстук, получит рубашку за сертификат.
В ответ запишите, сколько рублей заплатит И. за покупку в этом случае.
Ответ:
13
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ:
14
На рисунках изображены графики функций вида Установите соответствие между графиками функций и знаками коэффициентов a и c.
ФУНКЦИИ
А)
Б)
В)
Г)
КОЭФФИЦИЕНТЫ
1)
2)
3)
4)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
15
В окружности с центром O проведён диаметр AB и на окружности взята точка C так, что угол COB равен 120°, AC = 50. Найдите диаметр окружности.
Ответ:
16
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Ответ:
17
На координатной прямой отмечены точки A, B, C, и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
18
Если в маршрутном такси заняты все места, то оно трогается от остановки. Выберите утверждения, которые следуют из приведённых данных.
1) Если в маршрутке есть свободные места, то она не трогается
2) Если маршрутка продолжает стоять, то в ней остались свободные места
3) Если на каждом месте маршрутки сидит пенсионер, то она трогается от остановки
4) Если маршрутка отъехала от остановки, то в ней заняты все места
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ:
19
Найдите четырёхзначное число, кратное 22, произведение цифр которого равно 24. В ответе укажите какое-нибудь одно такое число.
Ответ:
20
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Ответ:
21
В обменном пункте можно совершить одну из двух операций:
1) за 3 золотых монеты получить 4 серебряных и одну медную;
2) за 6 серебряных монет получить 4 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
307 вариант по егэ математика
2 тренировочных варианта №307 Алекса Ларина пробный ОГЭ 2022 по математике 9 класс с ответами и решением по новой демоверсии ФИПИ ОГЭ 2022 года для подготовки к экзамену, дата выхода варианта на сайте: 5.01.2022 (5 января 2022 года)
Тренировочный вариант №307: вариант | ответы
Усложненная версия варианта: вариант | ответы
Вариант Алекса Ларина №307 ОГЭ 2022 по математике 9 класс:
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно.
Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола.
Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой.
1)Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
Ответ: 4215
2)Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?
Ответ: 17
3)Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Ответ: 5,13
4)Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.
Ответ: 1,5
5)Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт ∙ ч. Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.
Ответ: 7
10)Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечётное число очков.
Ответ: 0,5
11)Ниже представлены графики функций и формулы, которые из задают. Установите соответствие между графиками функций и формулами, которые их задают. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов, запятых и других разделительных символов.
Ответ: 132
14)Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Дойдя до нормы 40 капель в день, он ещё 2 дня (всего три дня) пьёт по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до пяти капель в последний день. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 200 капель)?
Ответ: 2
15)Два угла вписанного в окружность четырехугольника равны 164 и 93 градуса. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Ответ: 87
18)Радиусы всех полукругов равны 7. Красный четырёхугольник – квадрат. Найдите площадь, окрашенную в зелёный цвет.
Ответ: 196
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) Один из углов треугольника всегда не превышает 60 градусов. 2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. 3) Диагонали прямоугольника точкой пересечения делятся пополам.
Ответ: 13
25)Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площади ромба к площади параллелограмма, если отношение диагоналей параллелограмма равно 53.
Ответ: 53/1458
Вариант Алекса Ларина №2
На рисунке (см. выше) изображён план местности. Сторона каждой клетки на плане соответствует 2 км. Антон Сергеевич живёт в деревне Котенково. В субботу он хочет съездить в районный центр Псово. Туда можно добраться по прямой грунтовой дороге, а можно доехать по шоссе до посёлка Хомяковка и свернуть под прямым углом на другое шоссе, ведущее в Псово. Есть и третий путь: от Котенково по другой грунтовой дороге, ведущей вдоль рощи, добраться до деревни Попугаевка, где свернуть на шоссе, ведущее к посёлку Псово. Грунтовые дороги образуют с шоссе прямоугольные треугольники. По шоссе Антон Сергеевич едет со скоростью 72 км/ч, а по грунтовой дороге – 50 км/ч.
1)Пользуясь описанием, определите, какими цифрами обозначены на плане населённые пункты. Заполните таблицу. В ответе запишите три цифры без пробелов, запятых и других разделительных символов.
Ответ: 2341
2)Сколько километров проедет Антон Сергеевич, если поедет по шоссе через посёлок Хомяковка?
Ответ: 82
3)Найдите расстояние (в км) по прямой грунтовой дороге от Котенково до Псово.
Ответ: 58
4)Сколько минут потратит Антон Сергеевич на дорогу, если поедет мимо рощи через деревню Попугаевка?
Ответ: 70
5)В таблице (см. ниже) указана стоимость в рублях некоторых товаров в четырёх магазинах, расположенных в населённых пунктах. Антон Сергеевич хочет купить 2 булки белого хлеба, 4 кг зелёных яблок и 0,5 кг сала. Найдите, в каком магазине такой набор продуктов стоить дешевле всего. В ответе запишите стоимость (в рублях) этого набора продуктов в этом магазине.
Ответ: 562
14)На клетчатой бумаге с размером клетки 1 × 1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 140.
Ответ: 19740
15)Дан треугольник со сторонами 12, 15, 18. Проведена окружность, касающаяся обеих меньших сторон и имеющая центр на большой стороне. Найдите отрезки, на которые центр окружности делит большую сторону треугольника. В ответе запишите произведение найденных значений.
Ответ: 80
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) В параллелограмме есть два равных угла. 2) В тупоугольном треугольнике все углы тупые. 3) Площадь прямоугольника равна произведению длин всех его сторон.
Ответ: 1
21)На сайте проводится опрос, кого из 134 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста – доля голосов, отданных за него, в процентах, округлённая до целого числа. Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Ответ: 167
23)Каждая из трёх различных прямых делит площадь плоской фигуры пополам. Найдите наибольшую возможную площадь фигуры, заключённую внутри треугольника, образованного этими прямыми, если известно, что площадь фигуры равна 8.
Ответ: 2
24)Докажите, что проекции основания высоты треугольника на стороны, её заключающие, и на две другие высоты лежат на одной прямой.
10 Определите вероятность того, что при бросании игрального кубика правильной кости выпадет нечётное число очков.
100ballnik. com
22.06.2018 23:07:24
2018-06-22 23:07:24
Источники:
Https://100ballnik. com/%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%D0%B0%D0%BB%D0%B5%D0%BA%D1%81%D0%B0-%D0%BB%D0%B0%D1%80%D0%B8%D0%BD%D0%B0-%E2%84%96307-%D0%BF%D1%80%D0%BE%D0%B1%D0%BD%D1%8B%D0%B9-%D0%BE%D0%B3%D1%8D-2022/
Вариант 307 ЕГЭ Ларин. Первая часть | ЕГЭ профиль » /> » /> .keyword { color: red; } 307 вариант по егэ математика
Вариант 307 ЕГЭ Ларин. Первая часть
Вариант 307 ЕГЭ Ларин. Первая часть
1. Для распечатки 302 страниц были использованы две копировальные машины. Первая работала 8 минут, вторая 10 минут. Сколько страниц в минуту печатает первая
Машина, если первая печатает в минуту на 4 страницы больше, чем вторая?
2. На рисунке изображен график, описывающий прямолинейное движение автомобиля. По горизонтальной оси отложено время (в часах), по вертикальной —
Расстояние от пункта А (в километрах). Известно, что через 180 минут после начала движения автомобиль достиг пункта В и продолжил движение. Определите расстояние в километрах между пунктами А и В.
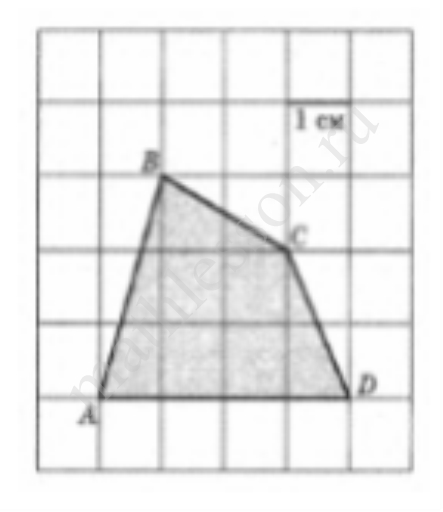
3. Найдите площадь четырехугольника ABCD. Размер каждой клетки 1см х 1 см. Ответ выразите в квадратных см.
4. Петя и Таня независимо друг от друга загадывают по одной цифре. С какой вероятностью сумма этих цифр окажется больше 16?
5. Найдите корень уравнения ( (0,2)^=frac(0,04)^ )
6. Найдите периметр параллелограмма ABCD, если AD=10, BD=8, а отрезок, соединяющий вершину В с серединой стороны AD, равен √15
7. Наблюдение за космическим телом показало, что расстояние S (в километрах) между этим телом и Землей увеличивается по закону ( S=1,8*10^5+0,5*10^5sqrt ) где
T — время в секундах от момента начала наблюдения. Через сколько секунд после начала наблюдения скорость удаления тела от Земли составит ( 10^3 ) км/с?
8. Точки M и N расположены на окружностях верхнего и нижнего основания цилиндра, радиус основания которого равен 2, а высота — 3. Длина отрезка MN равна 4. Через отрезок MN проведена плоскость, параллельная образующей цилиндра. Найдите расстояние от оси цилиндра до этой плоскости.
10. Плоский замкнутый контур площадью ( S=0,5 ) м^2, находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной
Индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой ( E=aScosα ) , где α – острый угол между направлением магнитного поля и перпендикуляром к контуру, ( a=4*10^ ) Тл/спостоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м2).
При каком минимальном угле α (в градусах) ЭДС индукции не будет превышать ( 10^ ) В?
11. Первый раствор содержит 20% азотной кислоты и 80% воды, второй ‐ 60% кислоты и 40% воды. Первая смесь была получена из 15 л первого раствора и некоторого количества второго раствора. Смешав то же самое количество второго раствора с 5 л первого раствора, получили вторую смесь. Сколько литров второго раствора было использовано для приготовления первой смеси, если процентное содержание воды во второй смеси вдвое больше процентного содержания кислоты в первой?
Найдите расстояние от оси цилиндра до этой плоскости.
Gdz-larin. ru
06.01.2020 21:01:49
2020-01-06 21:01:49
Источники:
Https://gdz-larin. ru/?p=6558
Вариант 307 Ларина, решение ЕГЭ математика 2020 | Виктор Осипов » /> » /> .keyword { color: red; } 307 вариант по егэ математика
307 вариант Алекса Ларина. Разбор ЕГЭ математика 2020
307 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
ВАЖНО: ТЕПЕРЬ РЕШЕНИЕ КАЖДОГО ЗАДАНИЯ РАСПОЛОЖЕНО ПОД ТЕКСТОМ САМИХ ЗАДАНИЙ! ВИДЕО НАЧИНАЕТСЯ С МОМЕНТА РЕШЕНИЯ САМОГО ЗАДАНИЯ. ЕСЛИ НУЖНО НАЧАТЬ ЗАНОВО, И ЛЕНЬ КРУТИТЬ, ПРОСТО ПЕРЕЗАГРУЗИТЕ СТРАНИЦУ. ТАК ЖЕ ДЛЯ НЕКОТОРЫХ ЗАДАНИЙ ПРЕДСТАВЛЕНЫ PDF РЕШЕНИЯ, ИНОГДА ОНИ НЕМНОГО ДОЛГО ГРУЗЯТСЯ
Задание 1
Для распечатки 302 страниц были использованы две копировальные машины. Первая работала 8 минут, вторая 10 минут. Сколько страниц в минуту печатает первая машина, если первая печатает в минуту на 4 страницы больше, чем вторая?
Задание 2
На рисунке изображен график, описывающий прямолинейное движение автомобиля. По горизонтальной оси отложено время (в часах), по вертикальной — расстояние от пункта А (в километрах). Известно, что через 180 минут после начала движения автомобиль достиг пункта В и продолжил движение. Определите расстояние в километрах между пунктами А и В.
Задание 3
Найдите площадь четырехугольника ABCD. Размер каждой клетки 1см х 1 см. Ответ выразите в квадратных см.
Задание 4
Петя и Таня независимо друг от друга загадывают по одной цифре. С какой вероятностью сумма этих цифр окажется больше 16?
Задание 5
Найдите корень уравнения $$(0,2)^=fraccdot (0,04)^$$
Задание 6
Найдите периметр параллелограмма ABCD, если AD=10, BD=8, а отрезок, соединяющий вершину В с серединой стороны AD, равен $$sqrt$$.
Задание 7
Наблюдение за космическим телом показало, что расстояние (в километрах) между этим телом и Землей увеличивается по закону $$S=1,8cdot 10^+0,5cdot10^sqrt$$, где t — время в секундах от момента начала наблюдения. Через сколько секунд после начала наблюдения скорость удаления тела от Земли составит 10 3 км/с?
Задание 8
Точки M и N расположены на окружностях верхнего и нижнего основания цилиндра, радиус основания которого равен 2, а высота — 3. Длина отрезка MN равна 4. Через отрезок MN проведена плоскость, параллельная образующей цилиндра. Найдите расстояние от оси цилиндра до этой плоскости.
Задание 9
Задание 10
Плоский замкнутый контур площадью S=0,5 м 2 , находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой $$epsilon=aScos alpha$$, где $$alpha$$ – острый угол между направлением магнитного поля и перпендикуляром к контуру, $$a=4cdot 10^$$ Тл/с – постоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м 2 ). При каком минимальном угле $$alpha$$ (в градусах) ЭДС индукции не будет превышать 10 -4 В?
Задание 11
Первый раствор содержит 20% азотной кислоты и 80% воды, второй ‐ 60% кислоты и 40% воды. Первая смесь была получена из 15 л первого раствора и некоторого количества второго раствора. Смешав то же самое количество второго раствора с 5 л первого раствора, получили вторую смесь. Сколько литров второго раствора было использовано для приготовления первой смеси, если процентное содержание воды во второй смеси вдвое больше процентного содержания кислоты в первой?
Задание 12
Задание 13
Задание 14
В правильной шестиугольной пирамиде SABCDEF с вершиной S через сторону основания АВ проведена плоскость, делящая боковые ребра противоположной грани пополам.
Б) Найдите площадь сечения пирамиды этой плоскостью, если сторона основания равна 1, а высота пирамиды равна 3/2
Задание 15
Задание 16
Пятиугольник ABCDE вписан в окружность единичного радиуса. Известно, что $$AB=sqrt$$, $$angle ABE=frac<pi>$$, $$angle EBD=frac<pi>$$; BC=CD
Задание 17
Химический комбинат получил заказ на изготовление этилового спирта, соляной кислоты и дистиллированной воды. Для готовой продукции потребовалась 21 железнодорожная цистерна. При перекачивании были использованы три специализированных насоса: сначала первый насос наполнил четыре цистерны этиловым спиртом, затем второй насос наполнил шестнадцать цистерн соляной кислотой и в завершение третий наос наполнил одну цистерну дистиллированной водой. Найдите минимально возможное время, затраченное на перекачивание всех продукции, если известно, что суммарная производительность всех насосов равна семи цистернам в сутки
Задание 18
Найдите все значения параметра $$ain [-6;6]$$ при которых неравенство $$(a+3)cdot ((x+1)(a+2)+3x)>0$$ выполняется при любых $$x geq 0$$.
Задание 19
На клетчатой бумаге нарисован прямоугольник размера $$mtimes n$$ клеток и проведена его диагональ. Все вершины прямоугольника лежат в узлах сетки и стороны прямоугольника не пересекают клетки.
307 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
ВАЖНО: ТЕПЕРЬ РЕШЕНИЕ КАЖДОГО ЗАДАНИЯ РАСПОЛОЖЕНО ПОД ТЕКСТОМ САМИХ ЗАДАНИЙ! ВИДЕО НАЧИНАЕТСЯ С МОМЕНТА РЕШЕНИЯ САМОГО ЗАДАНИЯ. ЕСЛИ НУЖНО НАЧАТЬ ЗАНОВО, И ЛЕНЬ КРУТИТЬ, ПРОСТО ПЕРЕЗАГРУЗИТЕ СТРАНИЦУ. ТАК ЖЕ ДЛЯ НЕКОТОРЫХ ЗАДАНИЙ ПРЕДСТАВЛЕНЫ PDF РЕШЕНИЯ, ИНОГДА ОНИ НЕМНОГО ДОЛГО ГРУЗЯТСЯ
Для распечатки 302 страниц были использованы две копировальные машины. Первая работала 8 минут, вторая 10 минут. Сколько страниц в минуту печатает первая машина, если первая печатает в минуту на 4 страницы больше, чем вторая?
При каком минимальном угле alpha в градусах ЭДС индукции не будет превышать 10 -4 В.
Mathlesson. ru
03.04.2018 17:30:30
2018-04-03 17:30:30
Источники:
Https://mathlesson. ru/larin307var-ege
Решение и ответы заданий Варианта №8 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
Найдите корень уравнения log4 25x+7 = 3.
Задание 2.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России.
Задание 3.
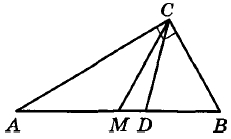
Угол между биссектрисой CD и медианой СМ проведёнными из вершины прямого угла С треугольника АВС, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Задание 4.
Найдите значение выражения frac{a^{3,33}}{ a^{2,11}cdot a^{2,22}} при а = frac{2}{7}.
Задание 5.
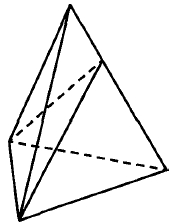
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Задание 6.
Прямая у = 9х + 6 является касательной к графику функции у = ах2 – 19х + 13. Найдите а.
Ответ задания: 28.
Задание 7.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 километра. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Ответ задания: 43,75.
Задание 8.
Первый садовый насос перекачивает 10 литров воды за 5 минут, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литра воды?
Ответ задания: 21.
Задание 9.
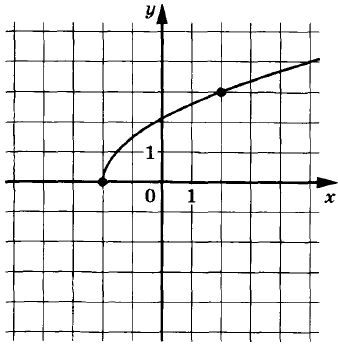
На рисунке изображён график функции f(x) = ksqrt{x+p}. Найдите f(0,25).
Задание 10.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Задание 11.
Найдите наибольшее значение функции у = 2х2 – 12х + 8lnх – 5 на отрезке [frac{12}{13};frac{14}{13}].
Задание 12.
а) Решите уравнение 7cosx – 4cos3x = 2√3sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–4π; –3π].
Ответ задания: a)frac{pi}{2}+pi k,k in Z;frac{pi}{3}+2pi n,n in Z;frac{2pi}{3}+2pi m,m in Z;б)-frac{11pi}{3};-frac{7pi}{2};-frac{10pi}{3}.
Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.
а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = 2AC.
Задание 14.
Решите неравенство log52(x4) – 28log0,04 (x2) ≤ 8.
Ответ задания: [–sqrt[4]{5}; –0,04]; [0,04; sqrt[4]{5}].
Задание 15.
Производство х тыс. единиц продукции обходится в q = 3х2 + 6х + 13 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?
Ответ задания: 24.
Задание 16.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Задание 17.
Найдите все значения а, при каждом из которых система уравнений
имеет единственное решение.
Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<2
а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{5}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{8}]+[frac{n}{23}]=n+2021?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
21 апреля 2016
В закладки
Обсудить
Жалоба
26 вариантов по 10 заданий для проведения самостоятельных работ.
26v-baze.docx
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
ОГЭ по математике. Тренировочный вариант СтатГрад
Видеоуроки ОГЭ | Вчера, 21:46
Решение тестовой части (№1-19) тренировочной работы по математике от 18 апреля 2022 года.
Тренировочные варианты базового ЕГЭ по математике с ответами.admin2018-11-03T15:52:01+03:00
Тренировочный вариант №10 базового ЕГЭ.
Тренировочный вариант №9 базового ЕГЭ.
Тренировочный вариант №8 базового ЕГЭ.
Тренировочный вариант №7 базового ЕГЭ.
Тренировочный вариант №6 базового ЕГЭ.
Тренировочный вариант №5 базового ЕГЭ.
Тренировочный вариант №4 базового ЕГЭ.
Тренировочный вариант №3 базового ЕГЭ.
Тренировочный вариант №2 базового ЕГЭ.
Тренировочный вариант №1 базового ЕГЭ.
- ЕГЭ по математике профиль
Пробные и тренировочные варианты ЕГЭ 2022 по математике (база) из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (база)
Структура варианта КИМ ЕГЭ 2022 математика база
Экзаменационная работа включает в себя 21 задание с кратким ответом базового уровня сложности.
Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Ответом к каждому из заданий 1–21 является целое число, или конечная десятичная дробь, или последовательность цифр.
Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов № 1 в той форме, которая предусмотрена инструкцией по выполнению задания.
Распределение заданий варианта КИМ ЕГЭ по содержанию, видам умений и способам действий
В экзаменационной работе проверяется следующий учебный материал.
1. Математика, 5–6 классы.
2. Алгебра, 7–9 классы.
3. Алгебра и начала анализа, 10–11 классы.
4. Теория вероятностей и статистика, 7–9 классы.
5. Геометрия, 7–11 классы
Связанные страницы:
Ресурс носит неофициальный информационно-справочный характер, персональные данные не собирает и не обрабатывает, на интеллектуальные права третьих лиц не претендует.
Все ссылки ведут напрямую на официальные сайты описываемых услуг.
Карта сайта
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант №41054170 с ответами
-
Тренировочный вариант №41054171 с ответами
-
Тренировочный вариант №41054172 с ответами
-
Тренировочный вариант №41054173 с ответами
-
Тренировочный вариант №41054174 с ответами
-
Тренировочный вариант №41054175 с ответами
-
Тренировочный вариант №41054176 с ответами
-
Тренировочный вариант №41054177 с ответами
-
Тренировочный вариант №41054178 с ответами
-
Тренировочный вариант №41054179 с ответами
-
Тренировочный вариант №41054180 с ответами
-
Тренировочный вариант №41054181 с ответами
-
Тренировочный вариант №41054182 с ответами
-
Тренировочный вариант №41054183 с ответами
-
Тренировочный вариант №41054184 с ответами
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами