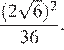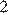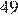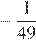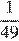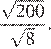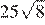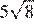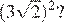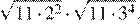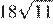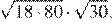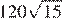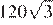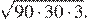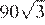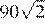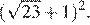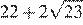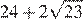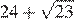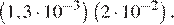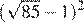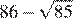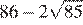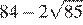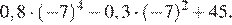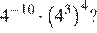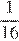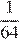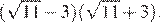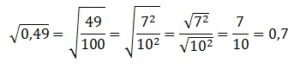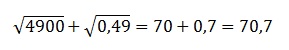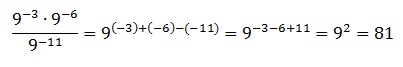Решу егэ математика 137285

Задания

Версия для печати и копирования в MS Word

Тип 8 № 137285

Найдите значение выражения 5 корень из 11 умножить на 2 корень из 2 умножить на корень из 22.

Спрятать решение

Решение.

Упростим выражение, разложив подкоренные выражения на множители и вынесем за знак корня полные квадраты чисел:

5 корень из 11 умножить на 2 корень из 2 умножить на корень из 22=5 умножить на корень из 11 умножить на 2 умножить на корень из 2 умножить на корень из 2 умножить на 11=5 умножить на 2 умножить на корень из 2 умножить на корень из 2 умножить на корень из 11 умножить на корень из 11=5 умножить на 2 умножить на 2 умножить на 11=220.

Ответ: 220.

Аналоги к заданию № 137285: 357566 392840 392866 392894 392921 392947 392973 159381 159383 159385 … Все

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Спрятать решение

·

·

Сообщить об ошибке · Помощь

Источник

Вычисления

1. Задание 8 № 137272

Найдите значение выражения

В ответе укажите номер правильного варианта.

1)

2)

3)

4) 4

2. Задание 8 № 137281

Вычислите:

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

3. Задание 8 № 137285

Найдите значение выражения .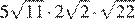

4. Задание 8 № 317389

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 5

2)

3)

4) 40

5. Задание 8 № 318630

Чему равно значение выражения

В ответе укажите номер правильного варианта.

1) 6

2) 12

3) 18

4) 36

6. Задание 8 № 337339

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 198

2)

3) 3564

4) 2178

7. Задание 8 № 337462

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 360

2)

3)

4)

8. Задание 8 № 337692

Найдите значение выражения (1,7 · 10− 5)(2 · 10− 2).

В ответе укажите номер правильного варианта.

1) 0,0000034

2) 34000000000

3) 0,000000034

4) 0,00000034

9. Задание 8 № 337700

Найдите значение выражения

В ответе укажите номер правильного варианта.

1)

2)

3)

4) 90

10. Задание 8 № 337782

Найдите значение выражения

В ответе укажите номер правильного варианта.

1)

2) 22

3)

4)

11. Задание 8 № 341194

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 2600000

2) 0,000026

3) 0,0000026

4) 0,00026

12. Задание 8 № 349896

Найдите значение выражения

1)

2)

3)

4)

13. Задание 8 № 352963

Какое из данных ниже чисел является значением выражения ?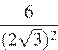

1)

2)

3)

4)

14. Задание 8 № 353384

Найдите значение выражения

15. Задание 8 № 355406

Какое из данных ниже чисел является значением выражения

1) 16

2)

3) −16

4)

16. Задание 8 № 369495

Найдите значение выражения

Задание 8 номер 137285

oleg681 год назад



0



0

Развернутый угол — это угол, стороны которого составляют прямую 
значит, углы 5:13 в сумме равны 180°
решим пропорцию
5+13=18
180:18=10
угол 1=5*10=50°
угол 2=13*10=130°

Посмотрите результаты тиража № 137285 лотереи «12/24» от 16 октября 2019 в 07:45. На сайте «Столото» вы можете проверить результаты розыгрыша по номеру билета. Кроме того, вы можете посмотреть, сколько билетов принимало участие в розыгрыше 137285 «12/24» от 16.10.2019, и узнать, как получить выигрыш.

Итоги розыгрыша

  • 7

  • 1

  • 8

  • 17

  • 19

  • 18

  • 21

  • 15

  • 10

  • 13

  • 16

  • 9

Угаданных чисел Выигравших комбинаций Выигрыш, ₽ Сумма выигрышей, ₽
0 или 12 0 0 0
1 или 11 0 0 0
2 или 10 0 0 0
3 или 9 7 240 1680
4 или 8 50 60 3000
Число билетов, принявших участие в розыгрыше, 266
Комбинаций 289
Общая сумма выигрышей, руб. 4680
Суперприз, руб. 1 478 400
В архиве тиража отображается сумма суперприза на начало тиража, которая разыгрывалась в этом тираже.

Как получить выигрыш?

Свойства числа 137285

Множители 5 * 27457
Делители 1, 5, 27457, 137285
Количество делителей 4
Сумма делителей 164748
Предыдущее целое 137284
Следующее целое 137286
Простое число? NO
Предыдущее простое 137279
Следующее простое 137303
137285th простое число 1831633
Является числом Фибоначчи? NO
Число Белла? NO
Число Каталана? NO
Факториал? NO
Регулярное число? NO
Совершенное число? NO
Полигональное число (s < 11)? NO
Двоичное 100001100001000101
Восьмеричная 414105
Двенадцатеричный 67545
Шестнадцатиричная 21845
Квадрат 18847171225
Квадратный корень 370.51990499837
Натуральный логарифм 11.82981433597
Десятичный логарифм 5.1376230880517
Синус -0.51639065240672
Косинус -0.85635313633277
Тангенс 0.60301134017924

Математические настройки для вашего сайта

Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
 中文
日本語
한국어

Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером


Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

© 2022
numberempire.com
Все права защищены

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

Мы больше не будем рекомендовать вам подобный контент.

Отмена

1) 75 — 69 = 6 (рулонов), в которых было 240м

2) 240 : 6 = 40 (м) ткани в одном рулоне

3) 40 * 75 = 3000 (м) оранжевой ткани

4) 40 * 69 = 2760 (м) синей ткани

Ответ: 3000м оранжевой ткани; 2760 м -синей ткани привезли в швейную

                                                                                       мастерскую.

———————————————————————————-

1км  = 100000см

Целеполагание

Диагностика

дата

Коррекция

В 1.1: знать определение квадратного корня из числа, арифметического квадратного корня из числа, обозначение корня, приближенное значение корня, возможности нахождения значения арифметического квадратного корня с любой степенью точности, уметь извлекать квадратный корень из числа

Д 1

1. Задание 3 № 205776 Какое из чисел отмечено на координатной прямой точкой A?

В ответе укажите номер правильного варианта.

 1)       2)        3)         4) 

9. Задание 3 № 340578 На координатной прямой отмечена точка А.

Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А?

 1)      2)         3) 0,6        4) 4

11. Задание 4 № 348386 Какое из данных чисел  является иррациональным?

1)    2)      3)   4) все эти числа рациональны

16.11

6. Задание 7 № 338423. Найдите значение выражения  при 

7 № 311910. Найдите значение выражения  при 

В 1.2: знать свойства арифметического корня, уметь использовать эти свойства при решении задач

Д2

1. Задание 4 № 137272

Найдите значение выражения 

В ответе укажите номер правильного варианта.      1)         2)       3)           4) 4

2. Задание 4 № 137268

Расположите в порядке возрастания числа: ; ; 5,5.

В ответе укажите номер правильного варианта.

1)        2)        3)          4) 

3. Задание 4 № 137285

Найдите значение выражения .

5. Задание 4 № 317389

Найдите значение выражения 

В ответе укажите номер правильного варианта.      1) 5        2)        3)       4) 40

8. Задание 4 № 337339

Найдите значение выражения 

В ответе укажите номер правильного варианта.      1) 198       2)        3) 3564     4) 2178

25. Задание 4 № 318729

Значение какого выражения является рациональным числом?

В ответе укажите номер правильного варианта.     

 1)      2)        3)      4) 

23.11

1. Задание 4 № 28

Значение какого из выражений является числом рациональным?

В ответе укажите номер правильного варианта.

1)         2)         3)             4) 

12. Задание 4 № 348417 Какое из данных ниже чисел является значением выражения ?

14. Задание 4 № 316557

Значение какого из выражений является числом иррациональным?

В ответе укажите номер правильного варианта.

1)         2)          3)         4) 

4. Задание 21 № 311255

Упростите выражение   

8. Задание 4 № 314246

Сравните числа  и 16.

В ответе укажите номер правильного варианта.

1)      2)       3) 

Решение.

Возведем в квадрат положительные числа и сравним:  

1)()2 = 67 +2 +61 = 128 + 2;

2) 162 = 256 = 128 + 128 = 128 + 2 · 64 = 128 +  = ;

3) Так как4087  ;

4) Так как  , то ()2  2 .
Учитывая, что  и 16 — положительные числа, получаем, что 

.Ответ: 1

12. Задание 21 № 311599

Какое из чисел больше:  или  ?

Дозирование домашнего задания

Удовлетворительно

Хорошо

Отлично

Домашняя работа 1

П.12, №№ 298 б, 299 а, в,300 б, г, е, 302 а, 304 а, в, д, 305 б, г

П. 12, № №307 а; 311 б, е

П.12, № №308 б, 314 в

П. 13, №№ 319 б, г, 320 а, б, г,  322 в, г, 327, 329 г, д. 323 а, б

П. 13, №№ 321 а, 330 а, в, 332 а, в

П. 13 № № 324 б, г, 331 б, г

П. 14, №№ 336 в, е, 339 б, в, 349 б, г

П. 14, №№ 337

П. 14, №№ 340 а

П. 15, №№  352 б, 356, 363 б, д, е, 365 б

П. 15, №№ 358 в, г, 365  г

П. 15, № 367 в, г

Домашняя работа 2

П. 16,  №№ 369 б, д, 370 а, д, е, 383 б, г, е, з, 385 а, в, д, ж, 386  б, г

П. 16, №№ 372 б, г, 373 а, в, 376 д, е, 387 б, в, д

П. 16, № 382 б, г

П. 17, №№ 393 г-е, 401 в, г, е, з, 402 б, г, е

П. 17, №№ 396 а, б, е, ж, 397 б, 399 а

П. 17, №№ 400 в, г, 403 в, г

Тема

А

В

С

Квадратный корень. Приближенное значение квадратного корня. Арифметический квадратный корень

К п. 12 есть К № 7,

 п. 13 – прочитать, записать в тетрадь, корни уравнения – 3 случая

п. 14 – прочитать

П.12, № 298 а, в, 299 б, г,300 а, в, д, 302 б ; 304 б, г, е,  305 а, д

П. 12, № № 307 б; 311 а, г

П.12, № №308 а, 314 а, б

П. 13, №№ 319 а, в, 320 в, д, е, 322 а, д, 328, 329 в, е , 323 в – е, 326

П. 13, №№ 321 б, 325, 330 б, г

П. 13 №№ 324 а, в,  331 а, в

П. 14, №№ 336 а, г, 339 а, 349 а, в

П. 14, №№ 341

П. 14, № 340 б

Функция у =  и ее график п. 15 – прочитать

П. 15, №№  352 а, 355, 363 а, в, г, 365 а

П. 15, №№ 358 а, б, 365 в

П. 15, № 367а, б

Свойства арифметического квадратного корня

П. 16,  №№ 369 а, г, 370 в, г, 383 а, в, д, ж,  385 б, г, е, з, 386  а, в, д

П. 16, №№ 372 а, в, 373 б, г, 376 в, г, 387 а, г, е

П. 16, № 382 а, в

П. 17, №№ 393 а — в, 401 а, д, ж,  402 а, в, д

П. 17, №№ 396 г, д, з,  397 а, 399 б

П. 17, №№ 400 а, б, 403 а, б

Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.

При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.

В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.

Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.

Теория к заданию №4

Из теоретического материала нам пригодятся правила обращения со степенями:

степени

Правила работы с подкоренными выражениями:koren

В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.

Разбор типовых вариантов задания №4 ОГЭ по математике

Первый вариант задания

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?

  1. 121n
  2. 11n+2
  3. 112n
  4. 11n+3
Решение:

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

  • при умножении степени складываются
  • приделении степени вычитаются
  • при возведении степени в степень степени перемножаются
  • при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.

121 • 11n = 112 • 11n

С учетом правила умножения, складываем степени:

  112 • 11n = 11n+2

Следовательно, нам подходит второй ответ.

Ответ: 2

Второй вариант задания

Значение какого из данных ниже выражений является наибольшим?

  1. 3√5
  2. 2√11
  3. 2√10
  4. 6,5
Решение:

Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:

  • 3√5

Переносим 3 под корень:

3√5 =  √(3² •5) = √(9•5) =  √45

  • 2√11

Переносим 2 под корень:

2√11 = √(2² • 11) = √(4 • 11) =√44

  • 2√10

Переносим 2 под корень:

2√10 = √(2² • 10) = √(4 • 10) =√40

  • 6,5

Возводим 6,5 в квадрат:

6,5 = √(6,5²) = √42,25

3-2

Посмотрим на все получившиеся варианты:

  1. 3√5 =  √45
  2. 2√11 = √44
  3. 2√10 = √40
  4. 6,5 = √42,25

Следовательно, правильный ответ первый

Ответ: 1

Третий вариант задания

Какое из данных чисел является рациональным?

  1. √810
  2. √8,1
  3. √0,81
  4. все эти числа иррациональны
Решение:

Для решения этой задачи нужно действовать следующим образом:

Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:

0,9

90

Рассмотри каждое из них:

0,9 = √(0,9)² = √0,81

90 = √(90²) = √8100

Следовательно, число √0,81 является рациональным, остальные же числа

  • √810
  • √8,1

хотя и похожи на форму 9 в квадрате, не являются рациональными.

Таким образом, правильный ответ третий.

Ответ: 3

Четвертый вариант задания

По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:

Какое из данных ниже чисел является значением выражения?

Разбор и решение задания №3 ОГЭ по математике

Разбор и решение задания №3 ОГЭ по математике

Решение:

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

16 — 14 = 2

Суммарно наши действия выглядят так:

Разбор и решение задания №3 ОГЭ по математике

Ответ: 4

Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!

Пятый вариант задания (демонстрационный вариант ОГЭ 2017)

Значение какого из выражений является рациональным числом?

  1. √6-3
  2. √3•√5
  3. (√5)²
  4. (√6-3)²
Решение:

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

Шестой вариант задания

Найдите значение выражения:

Задание №8 ОГЭ по математике

Решение:

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=72 и 100=102. И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:

Задание №8 ОГЭ по математике

По аналогии извлекаем и 2-й корень:

Задание №8 ОГЭ по математике

В итоге получаем:

Задание №8 ОГЭ по математике

Ответ: 70,7

Седьмой вариант задания

Найдите значение выражения:

Задание №8 ОГЭ по математике

Решение:

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

Задание №8 ОГЭ по математике

Ответ: 81

Источник

Вычисления

1. Задание 8 № 137272

Найдите значение выражения

В ответе укажите номер правильного варианта.

1)

2)

3)

4) 4

2. Задание 8 № 137281

Вычислите:

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

3. Задание 8 № 137285

Найдите значение выражения .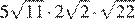

4. Задание 8 № 317389

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 5

2)

3)

4) 40

5. Задание 8 № 318630

Чему равно значение выражения

В ответе укажите номер правильного варианта.

1) 6

2) 12

3) 18

4) 36

6. Задание 8 № 337339

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 198

2)

3) 3564

4) 2178

7. Задание 8 № 337462

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 360

2)

3)

4)

8. Задание 8 № 337692

Найдите значение выражения (1,7 · 10− 5)(2 · 10− 2).

В ответе укажите номер правильного варианта.

1) 0,0000034

2) 34000000000

3) 0,000000034

4) 0,00000034

9. Задание 8 № 337700

Найдите значение выражения

В ответе укажите номер правильного варианта.

1)

2)

3)

4) 90

10. Задание 8 № 337782

Найдите значение выражения

В ответе укажите номер правильного варианта.

1)

2) 22

3)

4)

11. Задание 8 № 341194

Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 2600000

2) 0,000026

3) 0,0000026

4) 0,00026

12. Задание 8 № 349896

Найдите значение выражения

1)

2)

3)

4)

13. Задание 8 № 352963

Какое из данных ниже чисел является значением выражения ?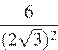

1)

2)

3)

4)

14. Задание 8 № 353384

Найдите значение выражения

15. Задание 8 № 355406

Какое из данных ниже чисел является значением выражения

1) 16

2)

3) −16

4)

16. Задание 8 № 369495

Найдите значение выражения

Источник

1. Задание 8 № 36

Упростите выражение (2 минус c) в степени 2 минус c(c плюс 4), найдите его значение
при c=0,5. В ответ запишите полученное число.

2. Задание 8 № 311910

Найдите значение выражения (2x плюс 3y) в степени 2 минус 3x левая круглая скобка дробь: числитель: 4, знаменатель: 3 конец дроби x плюс 4y правая круглая скобка  при x= минус 1,038, y= корень из 3.

3. Задание 8 № 318572

Упростите выражение  дробь: числитель: 9b, знаменатель: a минус b конец дроби умножить на дробь: числитель: a в степени 2 минус ab, знаменатель: 54b конец дроби  и
найдите его значение при a= минус 63, b=9,6. В
ответе запишите найденное значение.

4. Задание 8 № 338067

Найдите значение выражения (8b минус 8)(8b плюс 8) минус 8b(8b плюс 8) при b=2,6.

5. Задание 8 № 338092

Найдите f(7), если f(x плюс 5)=2 в степени (4 минус x) .

6. Задание 8 № 338175

Найдите f(1), если f(x −
2) = 85 − x.

7. Задание 8 № 338423

Найдите значение выражения 28ab плюс (2a минус 7b) в степени 2  при a= корень из 15,b= корень из 8.

1. Задание 8 № 311329

Упростите выражение  дробь: числитель: a в степени 2 плюс 4a, знаменатель: a в степени 2 плюс 8a плюс 16 конец дроби  и
найдите его значение при a= минус 2. В ответ запишите полученное
число.

2. Задание 8 № 311352

Упростите выражение   дробь: числитель: 2c минус 4, знаменатель: cd минус 2d конец дроби   и
найдите его значение при  c=0,5; d=5. В ответ запишите полученное
число.

3. Задание 8 № 311372

Упростите выражение   дробь: числитель: x в степени 2 минус 4, знаменатель: 4x в степени 2 конец дроби умножить на дробь: числитель: 2x, знаменатель: x плюс 2 конец дроби  
и найдите его значение при  x=4. В ответ запишите полученное число.

4. Задание 8 № 311463

Представьте в виде дроби выражение   дробь: числитель: 10x, знаменатель: 2x минус 3 конец дроби минус 5x  и
найдите его значение при  x=0,5. В ответ запишите полученное число.

5. Задание 8 № 311471

Упростите выражение   дробь: числитель: (a минус 2b) в степени 2 минус 4b в степени 2 , знаменатель: a конец дроби  
и найдите его значение при  a=0,3; b= минус 0,35.

6. Задание 8 № 311758

Найдите значение выражения  дробь: числитель: 64b в степени 2 плюс 128b плюс 64, знаменатель: b конец дроби : левая круглая скобка дробь: числитель: 4, знаменатель: b конец дроби плюс 4 правая круглая скобка  при b= минус дробь: числитель: 15, знаменатель: 16 конец дроби .

7. Задание 8 № 311814

Найдите значение выражения  левая круглая скобка a плюс дробь: числитель: 1, знаменатель: a конец дроби плюс 2 правая круглая скобка умножить на дробь: числитель: 1, знаменатель: a плюс 1 конец дроби  при a= минус 5.

8. Задание 8 № 311954

Найдите значение выражения  дробь: числитель: a(b минус 3a) в степени 2 , знаменатель: 3a в степени 2 минус ab конец дроби минус 3a при a=2,18, b= минус 5,6.

9. Задание 8 № 314312

Упростите выражение  дробь: числитель: 6c минус c в степени 2 , знаменатель: 1 минус c конец дроби : дробь: числитель: c в степени 2 , знаменатель: 1 минус c конец дроби . и
найдите его значение при c=1,2. В ответе запишите найденное
значение.

10. Задание 8 № 314315

Упростите выражение  дробь: числитель: xy плюс y в степени 2 , знаменатель: 15x конец дроби умножить на дробь: числитель: 3x, знаменатель: x плюс y конец дроби . и
найдите его значение при x=18 и y=7,5. В
ответе запишите найденное значение.

11. Задание 8 № 316255

Найдите значение выражения  левая круглая скобка дробь: числитель: a, знаменатель: 3 конец дроби плюс дробь: числитель: 3, знаменатель: a конец дроби плюс 2 правая круглая скобка умножить на дробь: числитель: 1, знаменатель: a плюс 3 конец дроби  при а =
6.

12. Задание 8 № 316344

Сократите дробь  дробь: числитель: (3x плюс 7) в степени 2 минус (3x минус 7) в степени 2 , знаменатель: x конец дроби .

13. Задание 8 № 319060

Найдите значение выражения  левая круглая скобка дробь: числитель: b, знаменатель: a конец дроби минус дробь: числитель: a, знаменатель: b конец дроби правая круглая скобка умножить на дробь: числитель: 1, знаменатель: b плюс a конец дроби  при a=1, b= дробь: числитель: 1, знаменатель: 3 конец дроби .

14. Задание 8 № 319072

Найдите значение выражения  дробь: числитель: 1, знаменатель: 4x конец дроби минус дробь: числитель: 4x плюс y, знаменатель: 4xy конец дроби  при x= корень из 42, y= дробь: числитель: 1, знаменатель: 2 конец дроби .

15. Задание 8 № 338095

Найдите значение выражения  дробь: числитель: 16, знаменатель: 4a минус a в степени 2 конец дроби минус дробь: числитель: 4, знаменатель: a конец дроби  при a= минус 12.

16. Задание 8 № 338131

Найдите значение выражения (a в степени 3 минус 25a) левая круглая скобка дробь: числитель: 1, знаменатель: a плюс 5 конец дроби минус дробь: числитель: 1, знаменатель: a минус 5 конец дроби правая круглая скобка  при a= минус 39.

17. Задание 8 № 338163

Найдите значение выражения (x минус 3): дробь: числитель: x в степени 2 минус 6x плюс 9, знаменатель: x плюс 3 конец дроби  при x= минус 21.

18. Задание 8 № 338181

Найдите значение выражения  левая круглая скобка дробь: числитель: a плюс 2b, знаменатель: a в степени 2 минус 2ab конец дроби минус дробь: числитель: 1, знаменатель: a конец дроби правая круглая скобка : дробь: числитель: b, знаменатель: 2b минус a конец дроби  при a=1,6,b= корень из 2 минус 1.

19. Задание 8 № 338274

Найдите значение выражения  дробь: числитель: 8ab, знаменатель: a плюс 8b конец дроби умножить на левая круглая скобка дробь: числитель: a, знаменатель: 8b конец дроби минус дробь: числитель: 8b, знаменатель: a конец дроби правая круглая скобка  при a=8 корень из 3 плюс 7,b= корень из 3 минус 3.

20. Задание 8 № 338448

Найдите значение выражения  левая круглая скобка дробь: числитель: y, знаменатель: 5x конец дроби минус дробь: числитель: 5x, знаменатель: y конец дроби правая круглая скобка :(y плюс 5x) при x= дробь: числитель: 1, знаменатель: 7 конец дроби ,y= дробь: числитель: 1, знаменатель: 4 конец дроби .

21. Задание 8 № 341704

Найдите значение выражения  левая круглая скобка дробь: числитель: 1, знаменатель: 5a конец дроби плюс дробь: числитель: 1, знаменатель: 7a конец дроби правая круглая скобка умножить на дробь: числитель: a в степени 2 , знаменатель: 4 конец дроби  при a =
7,7.

22. Задание 8 № 406539

Упростите выражение  дробь: числитель: a минус 2, знаменатель: a в степени 2 конец дроби : дробь: числитель: a минус 2, знаменатель: a в степени 2 плюс 3a конец дроби  и
найдите его значение при a = 1,5. В ответе запишите найденное
значение

1. Задание 8 № 137285

Найдите значение выражения 5 корень из 11 умножить на 2 корень из 2 умножить на корень из 22.

2. Задание 8 № 311383

Найдите значение выражения  a в степени (12) умножить на (a в степени ( минус 4) ) в степени 4   при
 a = минус дробь: числитель: 1, знаменатель: 2 конец дроби .

3. Задание 8 № 311467

Упростите выражение   дробь: числитель: a в степени ( минус 11) умножить на a в степени 4 , знаменатель: a в степени ( минус 3 конец дроби )  
и найдите его значение при  a= минус дробь: числитель: 1, знаменатель: 2 конец дроби . В ответе запишите
полученное число.

4. Задание 8 № 318630

Чему равно значение выражения (3 корень из 2) в степени 2 ?

5. Задание 8 № 337339

Найдите значение выражения  корень из 11 умножить на 2 в степени 2 умножить на корень из 11 умножить на 3 в степени 4 .

6. Задание 8 № 337700

Найдите значение выражения  корень из 90 умножить на 30 умножить на 3.

7. Задание 8 № 338076

Найдите значение выражения  дробь: числитель: 16x минус 25y, знаменатель: 4 корень из x конец дроби минус 5 корень из y минус корень из y, если  корень из x плюс корень из y=3.

8. Задание 8 № 350738

Найдите значение выражения:  дробь: числитель: 4x минус 25y, знаменатель: 2 корень из x конец дроби минус 5 корень из y минус 3 корень из y,
если  корень из x плюс корень из y=4

9. Задание 8 № 355406

Найдите значение выражения 4 в степени ( минус 10) умножить на левая круглая скобка 4 в степени 3 правая круглая скобка в степени 4 .

10. Задание 8 № 369495

Найдите значение выражения ( корень из 11 минус 3)( корень из 11 плюс 3).

11. Задание 8 № 370465

Найдите значение выражения  дробь: числитель: 1, знаменатель: корень из 5 конец дроби минус 2 минус дробь: числитель: 1, знаменатель: корень из 5 конец дроби плюс 2.

12. Задание 8 № 383598

Найдите значение выражения ( корень из 18 плюс корень из 2) умножить на корень из 2.

13. Задание 8 № 384401

Найдите значение выражения  дробь: числитель: 24 в степени 4 , знаменатель: 3 в степени 2 умножить на 8 в степени 3 конец дроби .

14. Задание 8 № 400942

Найдите значение выражения ( корень из 11 плюс 3 ) в степени 2 минус 6 корень из 11.

15. Задание 8 № 401223

Сколько целых чисел расположено
между 3 корень из 14  и 7 корень из 3 ?

16. Задание 8 № 401572

Сколько целых чисел расположено
между  корень из 5  и  корень из 95 ?

17. Задание 8 № 401984

Найдите значение выражения ( 2 плюс корень из 3 ) в степени (2) плюс ( 2 минус корень из 3 ) в степени (2) .

18. Задание 8 № 402481

Найдите значение выражения  корень из ( 4 корень из 2 минус 7 ) в степени (2) плюс 4 корень из 2 .

19. Задание 8 № 406280

Найдите значение выражения  дробь: числитель: корень из 21 умножить на корень из 14, знаменатель: корень из 6 конец дроби .

20. Задание 8 № 406567

Найдите значение выражения  дробь: числитель: 1, знаменатель: 4 в степени ( минус 10 конец дроби ) умножить на дробь: числитель: 1, знаменатель: 4 в степени (9 конец дроби ) .

21. Задание 8 № 412184

Найдите значение выражения a в степени (8) умножить на a в степени (17) colon a в степени (20)  при a=2.

22. Задание 8 № 412188

Найдите значение выражения  корень из a в степени (2) плюс 8ab плюс 16b в степени (2)  при a=3 дробь: числитель: 3, знаменатель: 7 конец дроби  и b= дробь: числитель: 1, знаменатель: 7 конец дроби .

23. Задание 8 № 412189

Найдите значение выражения  корень из дробь: числитель: 1, знаменатель: 16 конец дроби умножить на x в степени (6) y в степени (4)  при x=2  и y=5.

24. Задание 8 № 412191

Найдите значение выражения  корень из a в степени (8) умножить на ( минус a) в степени (4)  при a = 2.

25. Задание 8 № 412200

Сократите дробь  дробь: числитель: 45 в степени (n) , знаменатель: 3 в степени (2n минус 1 конец дроби умножить на 5 в степени n минус 2) .

26. Задание 8 № 412211

Найдите значение выражения  дробь: числитель: a в степени ( 23 ) умножить на ( b в степени (5) ) в степени (4) , знаменатель: ( a умножить на b ) в степени ( 20 конец дроби )  при a=2 и b= корень из 2 .

27. Задание 8 № 412229

Найдите значение выражения  дробь: числитель: корень из 25a в степени (9) умножить на корень из 16b в степени (8) , знаменатель: корень из a в степени (5 конец дроби b в степени 8)  при a = 4
и b = 7.

Источник

  • ЗАДАЧИ ЕГЭ С ОТВЕТАМИ

  • АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-14

Александр

26785

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Отзывов (2)

  1. Максим

    2016-07-18 в 02:03

    Потеряли знак минуса при вычислении синуса.

    Ответить

    • Александр

      2016-07-19 в 22:34

      Спасибо!

      Ответить

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

  • РубрикиРубрики
  • Задачи по номерам!

    №1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16

  • МЕТКИ

    БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие

  • ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если {cos xne 0}.

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам -4 pi , -2 pi , 0, 2 pi , 4 pi dots Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений x=frac{pi}{3}+2pi n , где n — целое, а найти надо корни на отрезке left [frac{5 pi}{2};frac{9 pi}{2} right ]. На указанном промежутке лежит точка 4 pi. От нее и будем отсчитывать. Получим: x=4 pi +frac{pi}{3}=frac{13 pi}{3}.

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение 2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}

б) Найдите все корни этого уравнения, принадлежащие промежутку left[-3pi right.;left.-frac{3pi }{2}right]

2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}

Упростим левую часть по формуле приведения.

2{{cos}^2 x+sqrt{3}{cos x}=0}

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок left[-3pi right.;left.-frac{3pi }{2}right].

Видим, что указанному отрезку принадлежат решения -frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.

Ответ: -frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам -4 pi , -2 pi , 0, 2 pi , 4 pi dots Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений x=frac{pi }{3}+2pi n, где n — целое, а найти надо корни на отрезке [frac{5pi }{2};frac{9pi }{2}]. На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: x=4pi +frac{pi }{3}=frac{13pi }{3}.

2. а) Решите уравнение {({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-pi ;frac{pi }{2}right].

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) 3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}

Степени равны, их основания равны. Значит, равны и показатели.

3{cos x{sin x}}=frac{3{cos x}}{2}

2{cos x{sin x-{cos x=0}}}

{cos x({sin x-frac{1}{2})=0}}

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку left[-pi ;frac{pi }{2}right].

Отметим на тригонометрическом круге отрезок left[-pi ;frac{pi }{2}right] и найденные серии решений.

Видим, что указанному отрезку принадлежат точки x=-frac{pi }{2} и x=frac{pi }{2} из серии x=frac{pi }{2}+pi n,nin z.

Точки серии x=frac{5pi }{6}+2pi n,nin z не входят в указанный отрезок.

А из серии x=frac{pi }{6}+2pi n,nin z в указанный отрезок входит точка x=frac{pi }{6}.

Ответ в пункте (б): -frac{pi }{2},frac{pi }{6} , frac{pi }{2}.

3. а) Решите уравнение {cos 2x}+{{sin}^2 x=0,5}

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-frac{7pi }{2}right.;left.-2pi right].

а)
{cos 2x}+{{sin}^2 x=0,5}

Применим формулу косинуса двойного угла: boldsymbol{cos2alpha =1-{2sin}^2alpha }

1-2{{sin}^2 x}+{{sin}^2 x}=0,5

{{-sin}^2 x=-0,5}

{{sin}^2 x=0,5}

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке left[-frac{7pi }{2}right.;left.-2pi right] с помощью двойного неравенства.

Сначала серия x=frac{pi }{4}+pi n,nin Z.

-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi

-frac{7}{2}le frac{1}{4}+nle -2

-3,75le nle -2,25

n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}

Теперь серия x=-frac{pi }{4}+pi n,nin Z

-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi

-frac{7}{2}le -frac{1}{4}+nle -2

-3,25le nle -1,75

n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}

n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}

Ответ: -frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4} .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии x=-frac{pi }{4}+2pi n,nin Z на отрезке left[-frac{pi }{2}right.;left.20pi right]. Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение left({tg}^2x-3right)sqrt{11{cos x}}=0.

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-frac{5pi }{2};-pi right].

Самое сложное здесь — область допустимых значений (ОДЗ). Условие {11cos x}ge 0 заметно сразу. А условие {cos x}ne 0 появляется, поскольку в уравнении есть {tg x=frac{{sin x}}{{cos x}}}.

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси Y.

Ответ в пункте а) x=pm frac{pi }{3}+2pi n, nin z

б) Отметим на тригонометрическом круге найденные серии решений и отрезок left[-frac{5pi }{2};-pi right].

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

x=frac{pi }{3}-2pi =-frac{5pi }{3} и x=-frac{pi }{3}-2pi =-frac{7pi }{3}.

5. а) Решите уравнение sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}

б) Найдите корни, принадлежащие отрезку [-pi ;4pi ].

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых {cos x}=frac{sqrt{2}}{2} или {cos x}=-frac{sqrt{2}}{2}. Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии x=-frac{3pi }{4}+2pi n не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие {cos x+{sin x}}ge 0. Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку [-pi ;4pi ] любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке left[-pi ;0right] нам подходит корень x =-frac{pi }{4}.

На отрезке left[0;2pi right] нам подходят корни x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}.

На отрезке left[2pi ;4pi right] — корни x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.

Ответ в пункте б): -frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

9 марта 2023

В закладки

Обсудить

Жалоба

Теория и практика.

Содержание

1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой
8) Тригонометрические функции
9) Показательные функции
10) Логарифмические функции

10_zadacha.pdf

Источник: vk.com/profimatika

Источник

Понравилась статья? Поделить с друзьями:
  • Решу егэ литература мцыри тест
  • Решу егэ математика 13173
  • Решу егэ литература мертвые души задания
  • Решу егэ литература мертвые души вариант
  • Решу егэ литература медный всадник вариант