ЕГЭ — 2016. Основная волна по математике 06.06.2016. Вариант 437. Юг
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
В летнем лагере 164 ребёнка и 23 воспитателя. Автобус рассчитан не более чем на 45 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Ответ:
2
На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведённой диаграмме, сколько месяцев среднемесячная температура превышала 20 градусов Цельсия.
Ответ:
3
На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.
Ответ:
4
Научная конференция проводится в 4 дня. Всего запланировано 30 докладов: в первые два дня по 9 докладов, остальные распределены поровну между третьим и четвёртыми днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?
Ответ:
5
Найдите корень уравнения
Ответ:
6
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Ответ:
7
На рисунке изображён график — производной функции
определённой на отрезке (−11; 2). Найдите абсциссу точки, в которой касательная к графику функции
параллельна оси абсцисс или совпадает с ней.
Ответ:
8
Объём треугольной пирамиды равен 94. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рис.). Найдите объём отсечённой треугольной пирамиды.
Ответ:
9
Найдите значение выражения
Ответ:
10
Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы:где t — время (в мин.), T0 = 680 К, а = −16 К/мин2, b = 224 К/мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
Ответ:
11
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Ответ:
12
Найдите точку минимума функции
Ответ:
13
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащего отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 16, а высота пирамиды равна 4. На рёбрах AB, CD и AS отмечены точки M, N и K соответственно, причём AM = DN = 4 и AK = 3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в млн рублей) | S | 0,8S | 0,5S | 0,1S | 0 |
Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Найдите все значение a, при каждом из которых уравнение
имеет ровно один корень.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8).
а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел.
б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7?
в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
10 апреля 2016
В закладки
Обсудить
Жалоба
Задания с экзамена + решения + критерии оценки.
Источник: alexlarin.net.
Подробные решения контрольных измерительных материалов Единого государственного экзамена по МАТЕМАТИКЕ от 06.06.2016. Профильный уровень. Основная волна
Условия КИМов реального ЕГЭ 2016 по математике (тип 1)
Часть 1
1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 сентября составляли 103 куб, м воды, а 1 октября — 114 куб. м. Сколько нужно заплатить за холодную воду за сентябрь, если стоимость 1 куб, м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
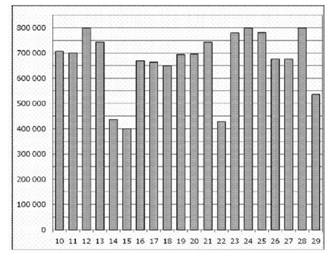
2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.
3. Найдите площадь треугольника, изображенного на рисунке.
4. В соревнованиях по толканию ядра участвуют 8 спортсменов из Великобритании, 6 спортсменов из Франции, 5 спортсменов из Германии и 5 — из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
5. Наидите корень уравнения: .
6. В четырехугольник , периметр которого равен 48 вписана окружность,
. Найдите
.
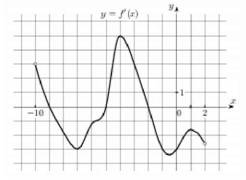
7. На рисунке изображён график производной функции
, определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.
8. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
Часть 2
9. Найдите значение выражений .
10. Груз массой 0,8 кг колеблется на пружине. Его скорость меняется по закону
. где
— время с момента начала колебаний,
— период колебаний,
м/с. Кинетическая энергия
(в джоулях) груза вычисляется по формуле
, где
— масса груза в килограммах,
— скорость груза в м/с.
Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях
11. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких же рубашек дороже куртки?
12. Найдите точку минимума функции
Тип 1
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку .
14. В правильной треугольной призме сторона основания
равна 6, а боковое ребро
равно 3 . На ребре
отмечена точка
так, что
. Точки
и
— середины ребер
и
соответственно. Плоскость
параллельна прямой
и содержит точки
и
.
а) Докажите, что прямая перпендикулярна плоскости
;
б) Найдите объем пирамиды, вершина которой — точка , а основание — сечение данной призмы плоскостью
.
15. Решите неравенство:
16. В трапеции боковая сторона
перпендикулярна основаниям. Из точки
на сторону
опустили перпендикуляр
. На стороне
отмечена точка
так, что прямые
и
перпендикулярны.
а) Докажите, что прямые и
параллельны.
б) Найдите отношение , если угол
.
17. 15-го января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наименьшее значение , при котором общая сумма выплат будет составлять более 1,25 млн рублей.
18. Найдите все значения параметра , при каждом из которых уравнение
имеет ровно три различных решения
19. На доске написаны числа 1, 2, 3, …,30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов, б (Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?
Подробные решения КИМов ЕГЭ №№1-12 и №№13-19(тип 1)
Условия КИМов основного ЕГЭ 2016 по математике (тип 2)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
14. В правильной четырехугольной пирамиде сторона основания
равна 16, а высота равна 4. На ребрах
и
отмечены точки
и
соответственно, причем
и
.
а) Докажите, что плоскости и
параллельны.
б) Найдите расстояние от точки до плоскости
.
15. Решите неравенство
16. В трапеции точка
— середина основания
, точка
— середина боковой стороны
. Отрезки
и
пересекаются в точке
.
а) Докажите, что площади четырехугольника и треугольника
равны
б) Найдите, какую часть от площади трапеции составляет площадь четырехугольника , если
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где
— целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
Найдите наибольшее значение , чтобы общая сумма выплат была меньше 50 млн рублей?
18. Найдите все значения , при каждом из которых уравнение
имеет единственный корень.
19. На доске написаны числа 2 и 3. За один ход разрешено заменить написанные на доске числа и
числами
и
(например, из чисел 2 и 3 можно получить либо 3 и 5, либо 5 и 5).
а) Может ли после нескольких ходов на доска появиться число 19?
б) может ли через 100 ходов на доске быть написано число 200?
в) укажите наименьшую разность чисел через 1007 ходов.
Условия КИМов основного ЕГЭ 2016 по математике (тип 3)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
14. В правильной треугольной призме сторона основания
равна 6, а боковое ребро
равно 3. На ребре
отмечена точка
так, что
. Точки
и
— середины ребер
и
соответственно. Плоскость у параллельна прямой
и содержит точки
и
.
а) Докажите, что прямая перпендикулярна плоскости
.
б) Найдите расстояние от точки до плоскости
.
15. Решите неравенство
16. В треугольнике проведены высоты
и
. На них из точек
и
опущены перпендикуляры
и
соответственно
а) Докажите, что прямые и
параллельны.
б) Найдите отношение , если угол
равен
.
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
Найдите наибольшее значение , при котором общая сумма выплат будет составлять менее 1,2 млн. рублей.
18. Найдите все значения , при каждом из которых уравнение
имеет ровно три различных решения.
Подробные решения КИМов ЕГЭ №№13-19(тип 2 и 3)
Условия КИМов основного ЕГЭ 2016 по математике (тип 4)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
14. В правильной треугольной пирамиде сторона основания
равна 12, а высота равна 1. На ребрах
и
отмечены точки
и
соответственно, причем
и
а) Докажите, что плоскости и
параллельны.
б) Найдите расстояние от точки до плоскости
.
15. Решите неравенство .
16. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17
а) Докажите, что данный четырехугольник — трапеция
б) Найдите отношение оснований этой трапеции
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где
— целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
Найдите наименьшее значение , чтобы общая сумма выплат была больше 10 млн рублей?
18. Найдите все значения , при каждом из которых уравнение
имеет единственный корень.
Подробные решения КИМов ЕГЭ №№13-19(тип 4)
2015-08-25
2018-08-30
2016
ЕГЭ 2016
Демоверсия ЕГЭ 2016
Демоверсия базового ЕГЭ по математике 2016
Демоверсия профильного ЕГЭ по математике 2016
Тренировочная работа по математике от 3 марта 2016
Профиль. варианты 1–4
Досрочный ЕГЭ от 28 марта 2016 г.
Вариант 1 (разбор заданий здесь)
Тренировочная работа по математике от 27 апреля 2016 г.
Профиль Восток, Запад (разбор заданий здесь на сайте)
База Восток, Запад
Реальный ЕГЭ по математике от 6 июня 2016
Основная волна (вариант 1)
Основная волна (вариант 2)
Разбор отдельных заданий на сайте Критерии
ЕГЭ по математике от 28 июня 2016 г. (резервный день)
Часть С
ОГЭ 2016
Демонстрационный вариант ОГЭ 2016
Демоверсия ОГЭ 2016
ОГЭ от 31 мая 2016
реальный экзамен
ЕГЭ математика — Профиль 2016-2021. Открытый банк заданий с ответами.