Решение 22 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
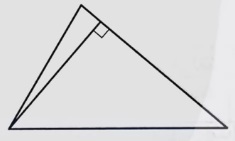
В треугольнике АВС высота СН равна 6, АВ=ВС, АС=8. Найдите синус угла АСВ.
В правильной треугольной призме (ABCA_1B_1C_1) все рёбра которой равны 2, найдите угол между прямыми (BB_1) и (AC_1). Ответ дайте в градусах.
Всего в группе туристов 21 человек, в том числе Лёня и Ваня. Группу случайным образом делят на три подгруппы по 7 человек для посадки в три микроавтобуса. Какова вероятность того, что Лёня и Ваня случайно окажутся в одном микроавтобусе?
Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,16. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Найдите корень уравнения (dfrac1{5x-14}=dfrac1{4x-3})
Найдите значение выражения (dfrac{{{log }_9 32 }}{{{log }_{27} 0{,}5 }})
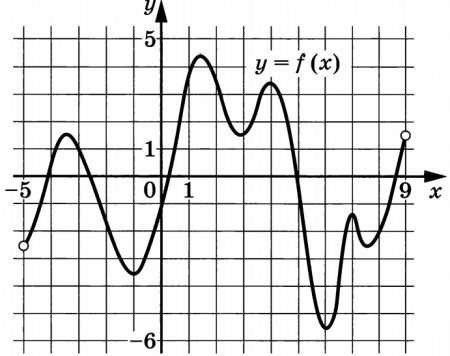
На рисунке изображён график функции (y= f(x)), определённой на интервале ((-5; 9)). Найдите количество решений уравнения (f ‘ (x)=0) на отрезке ([-2; 8]).
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением (a = 6500 ,км/ч^2). Скорость (v) (в км/ч) вычисляется по формуле (v=sqrt{2la}), где (l) — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 130 км/ч.
Теплоход проходит по течению реки до пункта назначения 416 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 21 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 50 часов. Ответ дайте в км/ч.
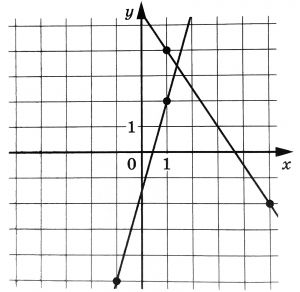
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Найдите точку максимума функции (y=left(5x-6right)cos x-5sin x -8), принадлежащую промежутку (left(0;dfrac{pi }{2}right))
а) Решите уравнение (cos 2x — sqrt{2}cos Big(dfrac{3pi}{2} + xBig) – 1 = 0).
б) Укажите корни этого уравнения, принадлежащие отрезку (Big[dfrac{3pi}{2}; 3piBig]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π |
В основании четырехугольной пирамиды (SABCD) лежит прямоугольник (ABCD) со сторонами (AB=8) и (BC=6). Длины боковых ребер пирамиды (SA=sqrt{21}), (SB=sqrt{85}), (SD=sqrt{57}).
а) Докажите, что (SA) – высота пирамиды.
б) Найдите угол между прямыми (SC) и (BD).
Решите неравенство (x^2log_{243} (-x-3)geqslant log_3 (x^2+6x+9))
В июле 2022 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы:
– каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– в июле 2023, 2024 и 2025 годов долг остаётся равным 220 тыс. рублей;
– выплаты в 2026 и 2027 годах равны;
– к июлю 2027 года долг будет выплачен полностью.
Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.
Две окружности разных радиусов касаются внешним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите ВС, если радиусы окружностей равны √15 и 15.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} sqrt{a-y^2}=sqrt{a-x^2} \ x^2+y^2=2x+4y end{cases}) имеет ровно два различных решения.
На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 1, к каждому числу из второй группы — цифру 8, а числа из третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 4 раза?
б) Могла ли сумма всех этих чисел увеличиться в 18 раз?
в) Сумма всех этих чисел увеличилась в 11 раз. Какое наибольшее количество чисел могло быть написано на доске?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5
5,832
9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1
0,216
9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2
51,2
9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8
281,25
9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19
60
9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4
30
9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9
0,6
9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7
1,8
9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1
756
9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18
220,5
9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1
50
9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4
40
9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4
33
9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39
23
9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2
0,32
9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4
1,16
9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2
175
9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28
43,75
9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2
115
9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25
220
9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2
6250
9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7
1,3
9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6
60
9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6
30
9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2
6
9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75
96
9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6
7
9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3
28
9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4
6,5
9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14
9,6
9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2
25
9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3
17
9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3
8
9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6
633
9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5
0,31
9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5
1,728
9) 756
10) -0,5
11) 30
Решение заданий варианта №22 из сборника ОГЭ 2023 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Слева от входа в квартиру располагаются кухня и санузел, причём площадь кухни больше площади санузла. Наименьшую площадь имеет кладовая. Из гостиной есть двери в коридор и на кухню. В квартире есть застеклённая лоджия, куда можно попасть, пройдя через спальню.
Задание 6.
Найдите значение выражения (frac{1}{12}-1frac{2}{15})cdot 6frac{2}{3}.
Задание 7.
Одно из чисел √29, √34, √39, √45 отмечено на прямой А.
Какое это число?
1)√29 2)√34 3)√39 4)√45
Задание 8.
Найдите значение выражения frac{(b^{–5})^{2}}{b^{–12}} при b = 5.
Задание 9.
Найдите корень уравнения (х + 2)2 = (1 – х)2.
Задание 10.
В магазине канцтоваров продаётся 120 ручек: 32 красные, 32 зеленые, 46 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Задание 11.
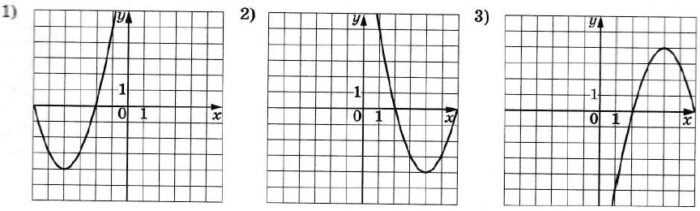
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ФОРМУЛЫ
А) у = х2 + 8х + 12
Б) у = х2 – 8х + 12
В) у = –х2 + 8х – 12
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле a = ω2R, где ω – угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 7,5 с-1, а центростремительное ускорение равно 337,5 м/с2. Ответ дайте в метрах.
Задание 13.
Укажите решение неравенства (х + 4)(х – > 0.
Задание 14.
В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 9-й день акция стоила 555 рублей, а в 13-й день – 631 рублей?
Задание 15.
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника.
Задание 16.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 92º, угол CAD равен 60º. Найдите угол ABD. Ответ дайте в градусах.
Задание 17.
Диагональ прямоугольника образует угол 63° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Задание 18.
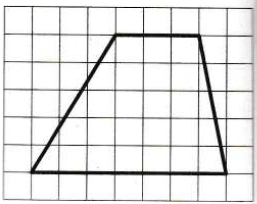
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Задание 19.
Какие из следующих утверждений верны?
1) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2) Если в ромбе один из углов равен 90 градусам, то этот ромб является квадратом.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
Задание 20.
Решите уравнение x6 = –(7х + 10)3.
Задание 21.
Два велосипедиста одновременно отправились в 224-километровый пробег. Первый ехал со скоростью, на 2 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.
Задание 22.
Постройте график функции у = х2 – 3|х| – х и определите, при каких значениях m прямая у = m имеет с графиком не менее одной, но не более трёх общих точек.
Задание 23.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:11:19. Найдите радиус окружности, если меньшая из сторон равна 15.
Задание 24.
Основания ВС и АD трапеции АВСВ равны соответственно 12 и 75, АС = 30. Докажите, что треугольники СВА и АСD подобны.
Задание 25.
Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если ВС = 2, а расстояние от точки K до стороны АВ равно 8.
Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 1
Найдите корень уравнения $$0,2^{5+4х}=125.$$
Ответ: -2
Скрыть
Значение $$0,2=frac{1}{5}=5^{-1},$$ а число $$125=5^3,$$ поэтому данное уравнение можно переписать так:
$$5^{-(5+4x)}=5^3$$
и перейти к равенству степеней:
$$-5-4x=3$$
$$4x=-8$$
$$x=-2$$
Задание 2
При производстве в среднем на каждые 1500 насосов приходится 36 неисправных.
Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Ответ: 0,024
Скрыть
Вероятность выбора неисправного насоса равна доли неисправных насосов, среди всех насосов в продаже:
$$P=frac{36}{1500}=0,024$$
Задание 3
В четырёхугольник ABCD вписана окружность, АВ = 8, ВС = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.
Ответ: 30
Скрыть
По свойству четырехугольника вписанного в окружность, имеем такое равенство длин его сторон:
$$AD+BC=AB+DC,$$
откуда
$$AD = AB+DC-BC$$
$$AD = 8+27-5 = 30$$
Задание 4
Найдите значение выражения: $$(3frac{1}{8}-1,5):frac{1}{56}$$
Ответ: 91
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 5
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна $$27sqrt{2}.$$ Найдите площадь боковой поверхности конуса.
Ответ: 27
Скрыть
Из площади боковой поверхности цилиндра
$$S_{бок}=2pi Rcdot h$$
найдем радиус основания, учитывая, что по условию задания h=R, получим:
$$2pi R^2=27sqrt{2}$$
$$R^2=frac{27sqrt{2}}{2pi}$$
Площадь боковой поверхности конуса, равна
$$S_{кон}=pi Rl,$$
где $$l=sqrt{R^2+R^2}=Rsqrt{2}$$ — образующая конуса. Подставляем ее величину в формулу площади поверхности, имеем:
$$S_{кон}=pi R^2sqrt{2}=sqrt{2}picdotfrac{27sqrt{2}}{2pi}=27$$
Задание 6
На рисунке изображён график $$y = f'(x)$$ — производной функции $$f(x),$$ определённой на интервале $$(-3; 8).$$ В какой точке отрезка $$[-2; 3]$$ функция $$f(x)$$ принимает наименьшее значение?
Ответ: 3
Скрыть
На отрезке $$[-2;3]$$ значение $$f'(x)leq0.$$ Тогда $$y=f(x)$$ на всём отрезке убывает или не возрастает. Тогда наименьшее значение $$f(x)$$ примет в конце отрезка, т.е. при $$x=3.$$
Задание 7
В телевизоре ёмкость высоковольтного конденсатора $$С = 5cdot10^{-6}$$ Ф. Параллельно с конденсатором подключён резистор с сопротивлением $$R = бcdot10^6$$ Ом. Во время работы телевизора напряжение на конденсаторе $$U_0 = 34$$ кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением $$t=alpha RClog_2frac{U_0}{U}$$ (с), где $$alpha=1,7$$ — постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошла 51 с.
Ответ дайте в киловольтах.
Ответ: 17
Скрыть
В задании даны следующие величины (запишем их в нужных единицах измерения):
$$C=5cdot10^{-6}$$
$$R=6cdot10^6$$
$$U_0=34$$
$$alpha=1,7$$
$$t=51$$
Подставим эти значения в формулу убывания напряжения, получим:
$$51=1,7cdot6cdot10^6cdot5cdot10^{-6}cdotlog_2frac{34}{U}$$
$$51=51cdotlog_2frac{34}{U}$$
$$log_2frac{34}{U}=1=log_2 2$$
$$frac{34}{U}=2Rightarrow U=frac{34}{2}=17$$
Задание 8
Плиточник должен уложить 120 м2 плитки. Если он будет укладывать на 8 м2 в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 9
На рисунке изображён график функции $$f(x) = kx + b.$$ Найдите значение $$x$$, при котором $$f(x) = -20,5.$$
Ответ: 13
Скрыть
Точки $$(3;-3)$$ и $$(-1;4)$$ принадлежат графику функции. Тогда:
$$left{begin{matrix} -3=kcdot3+b\ 4=kcdot(-1)+b end{matrix}right.Leftrightarrowleft{begin{matrix} -7=4k\ b=4+k end{matrix}right.Leftrightarrowleft{begin{matrix} k=-frac{7}{4}\ b=frac{9}{4} end{matrix}right.$$
Получили:
$$f(x)=-frac{7}{4}x+frac{9}{4}$$
Тогда:
$$-frac{7}{4}x+frac{9}{4}=-20,5$$
$$-7x+9=-82$$
$$-7x=-91$$
$$x=13$$
Задание 10
В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер достанут третьим по счёту?
Ответ: 0,15
Скрыть
$$P(к,к,с)=frac{3}{6}cdotfrac{2}{5}cdotfrac{3}{4}=frac{3}{20}=0,15$$
Задание 11
Найдите точку максимума функции $$y=x^{3}+18x^{2}+81x+23$$
Ответ: -9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 12
а) Решите уравнение $$2sin^{2}x-3sqrt{3}sin(frac{pi}{2}+x)-5=0$$.
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-pi]$$
Ответ: а)$$pm frac{5pi}{6}+2pi n,n in Z$$ б)$$-frac{7pi}{6}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 13
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 5. На ребре SC отмечена точка K, причём SK:KC=1:3. Плоскость а содержит точку K и параллельна плоскости SAD.
а) Докажите, что сечение пирамиды SACD плоскостью $$alpha$$ — трапеция.
б) Найдите объём пирамиды, вершиной которой является точка S, а основанием — сечение пирамиды SABCD Б плоскостью $$alpha$$.
Ответ: $$frac{5sqrt{17}}{8}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 14
Решите неравенство: $$log_{2}(18-9x)-log_{2}(x+2)>log_{2}(x^{2}-6x+8)$$
Ответ: $$(-2;1)cup (1;2)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн рублей? (Считайте, что округления при вычислении платежей не производятся.)
Ответ: 1,6 млн. руб.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 16
Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E.
а) Докажите, что $$angle EOC=angle ECO$$.
б) Найдите площадь треугольника ACE, если радиус описанной около треугольника ABC окружности равен $$6sqrt{3}$$, $$angle ABC=60$$.
Ответ: $$27sqrt{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Найдите все значения a, при каждом из которых уравнение
$$frac{left|x-6right|+a-6}{x^2-10x+a^2}=0$$
имеет ровно два различных корня.
Ответ: $$a<0; 0<a<3; 3<a<4; 4<a<5; 5<a<6$$
Скрыть
Преобразуем исходное уравнение:
$$frac{|x-6|+a-6}{x^2-10x+a^2}=0Leftrightarrowleft{begin{matrix} |x-6|=6-a,\ x^2-10x+a^2neq0 end{matrix}right.Leftrightarrowleft{begin{matrix} left[begin{matrix} x=a,\ x=12-a, end{matrix}right.\ aleq6,\ x^2-10x+a^2neq0. end{matrix}right.$$
Чтобы уравнение имело два различных корня, числа a и 12 − a должны быть различны, поэтому $$aneq12-a,$$ откуда $$aneq6.$$ Таким образом, $$a<6$$ и ни одно из чисел a и 12 − a не должно являться корнем уравнения $$x^2-10x+a^2=0.$$ Подставляя эти числа в уравнение $$x^2-10x+a^2,$$ найдем, при каких a они являются корнями:
1) из $$a^2-10a+a^2=0,$$ получаем: a=0 или a=5;
2) из $$(12-a)^2-10(12-a)+a^2=0,$$ получаем:
$$2a^2-14a+24=0Leftrightarrow a^2-7a+12=0Leftrightarrowleft[begin{matrix} a=3,\ a=4. end{matrix}right.$$
Тем самым одновременно: $$a<6,aneq0,aneq3,aneq4,aneq5.$$
Задание 18
В ящике лежит 58 овощей, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей, масса каждого из которых меньше 1000 г, равна 976 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1036 г.
а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г?
б) Могло ли в ящике оказаться ровно 12 овощей, масса каждого из которых равна 1000 г?
в) Какую наименьшую массу может иметь овощ в этом ящике?
Ответ: нет; нет; 240 гр.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
| 3267 | При производстве в среднем на каждые 1500 насосов приходится 36 неисправных. Найдите вероятность тог, что случайно выбранный насос окажется неисправным Решение |
При производстве в среднем на каждые 1500 насосов приходится 36 неисправных ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 2 |  |
| 3266 | Цилиндр и конус имеют общие основания и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 27sqrt2. Найдите площадь боковой поверхности конусаРешение |
Цилиндр и конус имеют общие основания и высоту ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 5 | |
| 3265 | В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер достанут третьим по счету?Решение |
В ящике 3 красных и 3 синих фломастера ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 10 | |
| 3264 | Найдите точку максимума функции y=x^3+18x^2+81x+23Решение  График |
Найдите точку максимума функции y=x3 + 18×2 +81x +23 ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 11 | |
| 2624 | Плиточник должен уложить 120 м2 плитки. Если он будет укладывать на 8 м2 в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?Решение |
Плиточник должен уложить 120 квадратных метров плитки ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 8 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 11 | |
| 2623 | Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E. а) Докажите, что /_EOC=/_ECO. б) Найдите площадь треугольника ACE, если радиус описанной около треугольника ABC окружности равен 6sqrt3, /_ABC=60^@ Решение |
Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 16 # Задача-аналог 2881 | |
| 2622 | а) Решите уравнение 2sin^2(x)-3sqrt(3)sin(pi/2+x)-5=0 б) Укажите корни этого уравнения, принадлежащие отрезку [-(5pi)/2; -pi].Решение График |
Решите уравнение 2sin квадрат x -3 корня из 3 sin(pi/2+x) -5 =0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 12 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 13 |
|
| 2621 | В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 5. На ребре SС отмечена точка K, причём SK:KC=1:3. Плоскость alpha содержит точку K и параллельна плоскости SAD. а) Докажите, что сечение пирамиды SABCD плоскостью alpha — трапеция. б) Найдите объём пирамиды, вершиной которой является точка S, а основанием — сечение пирамиды SABCD плоскостью alphaРешение |
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 14 | |
| 2620 | Решите неравенство log_{2}(18-9x) — log_{2}(x+2) > log_{2}(x^2-6x+8)Решение График |
Решите неравенство log_{2}(18-9x) — log_{2}(x+2) > log_{2}(x^2 -6x+8) ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 15 | |
Ответы к пособию для подготовки ЕГЭ-2023 по математике. Профильный уровень. Типовые экзаменационные варианты. Под редакцией И. В. Ященко. 36 вариантов.
| Вариант 1 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 5.5 | 10 | -4 |
| 2 | 2048 | 11 | -2910 |
| 3 | 0.06 | 12 |  |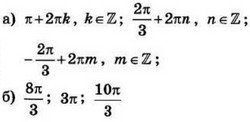
| 4 | 0.89 | 13 | б) 24 |
| 5 | -0.2 | 14 |  |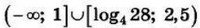
| 6 | 0.5 | 15 | 400 тыс. рублей |
| 7 | 5 | 16 | б) 14.2 |
| 8 | 5.832 | 17 | (-4; -3) ∪ (-3; -1) ∪ (-1; 0) |
| 9 | 2 | 18 | а) да; б) нет; в) 205 |
| Вариант 2 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 7.5 | 10 | -8 |
| 2 | 4 | 11 | 12.25 |
| 3 | 0.12 | 12 |  |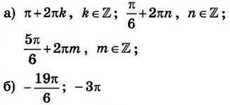
| 4 | 0.91 | 13 | б) 26 |
| 5 | -0.9 | 14 |  |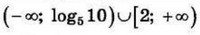
| 6 | 0.2 | 15 | 210 тыс. рублей |
| 7 | 1 | 16 | б) 29.7 |
| 8 | 0.216 | 17 | (0; 0.8) ∪ (0.8; 3.2) ∪ (3.2; 4) |
| 9 | 16 | 18 | а) да; б) нет; в) 195 |
| Вариант 3 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2.5 | 10 | 32 |
| 2 | 30 | 11 | 204 |
| 3 | 0.37 | 12 |  |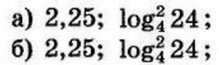
| 4 | 0.375 | 13 | б) 180 |
| 5 | -2.5 | 14 |  |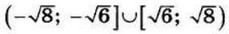
| 6 | 4 | 15 | 7.28 млн рублей |
| 7 | 2 | 16 | б) 32 |
| 8 | 51.2 | 17 |  |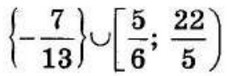
| 9 | 14 | 18 | а) да; б) да; в) 2295 |
| Вариант 4 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 1.5 | 10 | -56 |
| 2 | 12 | 11 | -10.9 |
| 3 | 0.24 | 12 |  |
| 4 | 0.125 | 13 | б) 40 |
| 5 | 0.375 | 14 |  |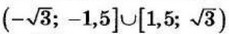
| 6 | 125 | 15 | 8 937 тыс. рублей |
| 7 | 8 | 16 | 42.16 |
| 8 | 281.25 | 17 |  |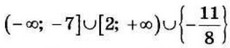
| 9 | 18 | 18 | а) да; б) нет; в) 897 |
| Вариант 5 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 99.5 | 10 | 16 |
| 2 | 12 | 11 | -52 |
| 3 | 0.004 или -0.004 | 12 |  |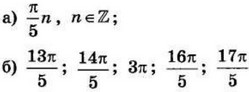
| 4 | 0.9409 | 13 |  |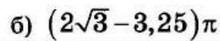
| 5 | -0.5 | 14 |  |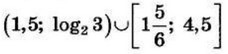
| 6 | 2 | 15 | 8.4 млн рублей |
| 7 | -19 | 16 | б) 9.1 |
| 8 | 60 | 17 |  |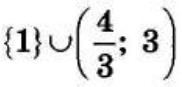
| 9 | 17 | 18 | а) нет; б) нет; в) 36 |
| Вариант 6 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 55 | 10 | -1 |
| 2 | 18 | 11 | -6 |
| 3 | 0.006 или -0.006 | 12 |  |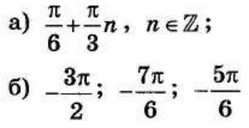
| 4 | 0.8464 | 13 |  |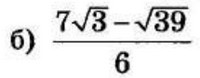
| 5 | -5.5 | 14 |  |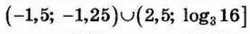
| 6 | 3 | 15 | 5.65 млн рублей |
| 7 | -4 | 16 |  |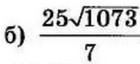
| 8 | 30 | 17 |  |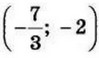
| 9 | 24 | 18 | а) нет; б) нет; в) 57, 58, 59, 60, 61 |
| Вариант 7 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.2 | 10 | 6 |
| 2 | 10 | 11 | 0.5 |
| 3 | 0.2 | 12 |  |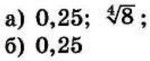
| 4 | 0.56 | 13 | б) 3 |
| 5 | -0.4 | 14 |  |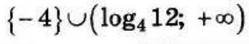
| 6 | -1 | 15 | 8 млн рублей |
| 7 | 9 | 16 | б) 6√2 |
| 8 | 0.6 | 17 |  |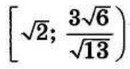
| 9 | 55 | 18 | а) да; б) нет; в) 79 |
| Вариант 8 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.4 | 10 | 0.25 |
| 2 | 5 | 11 | 17 |
| 3 | 0.125 | 12 |  |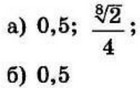
| 4 | 0.46 | 13 | 6√3 |
| 5 | -7 | 14 |  |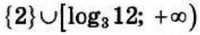
| 6 | -1 | 15 | 13 млн рублей |
| 7 | 7 | 16 |  |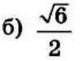
| 8 | 1.8 | 17 |  |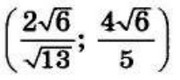
| 9 | 11 | 18 | а) да; б) нет; в) 73 |
| Вариант 9 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 3 | 10 | -3 |
| 2 | 15 625 | 11 | 9 |
| 3 | 0.01 | 12 |  |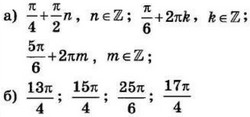
| 4 | 0.28 | 13 |  |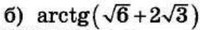
| 5 | -12 | 14 | (-∞; -1) |
| 6 | 144 | 15 | 7 млн рублей |
| 7 | -1 | 16 |  |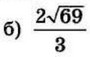
| 8 | 756 | 17 |  |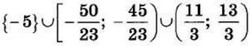
| 9 | 20 | 18 | а) да; б) нет; в) 176 |
| Вариант 10 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.6 | 10 | 253 |
| 2 | 150 | 11 | -23.25 |
| 3 | 0.28 | 12 |  |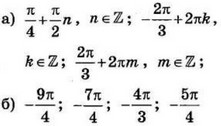
| 4 | 0.17 | 13 |  |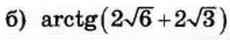
| 5 | -2.6 | 14 | (-∞; -2) |
| 6 | 625 | 15 | 4 млн рублей |
| 7 | -18 | 16 |  |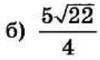
| 8 | 220.5 | 17 |  |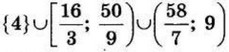
| 9 | 9 | 18 | а) нет; б) нет; в) 1933 |
| Вариант 11 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | -0.7 | 10 | 78 |
| 2 | 72 | 11 | 6.75 |
| 3 | 0.25 | 12 |  |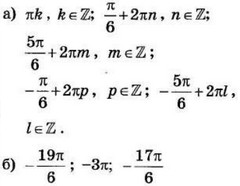
| 4 | 0.043 | 13 | б) 80√3 |
| 5 | -0.2 | 14 | (-∞; 0] ∪ [2; 3] |
| 6 | -5 | 15 | 600 тыс. рублей |
| 7 | -1 | 16 |  |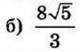
| 8 | 50 | 17 | {-5} ∪ (-1; 0) |
| 9 | 17.5 | 18 | а) да; б) нет; в) 97 |
| Вариант 12 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.75 | 10 | -23 |
| 2 | 24 | 11 | 6.25 |
| 3 | 0.55 | 12 |  |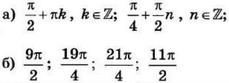
| 4 | 0.02 | 13 | б) 150 |
| 5 | -1.5 | 14 | (-∞; 0) ∪ (log53; 1) |
| 6 | -4 | 15 | 750 тыс. рублей |
| 7 | 4 | 16 |  |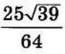
| 8 | 40 | 17 |  |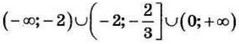
| 9 | 13.5 | 18 | а) да; б)нет; в) 85 |
| Вариант 13 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 8 | 10 | -0.5 |
| 2 | 48 | 11 | 77 |
| 3 | 0.4 | 12 | а) -2; -1 б) -1 |
| 4 | 0.6 | 13 | б) 5√3 |
| 5 | -9 | 14 | (1; 3] |
| 6 | 0.5 | 15 | 37 |
| 7 | 4 | 16 | б) 120/13 |
| 8 | 33 | 17 | [4√3; 12] |
| 9 | 9 | 18 | а) да; б) нет; в) 23/20 |
| Вариант 14 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 14 | 10 | 0.4 |
| 2 | 40.5 | 11 | 37 |
| 3 | 0.28 | 12 |  |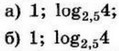
| 4 | 0.78 | 13 |  |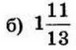
| 5 | -2 | 14 | [-3; -1) |
| 6 | 0.04 | 15 | 3 |
| 7 | 39 | 16 | б) 4 |
| 8 | 23 | 17 |  |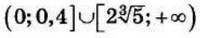
| 9 | 24 | 18 |  |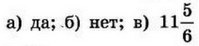
| Вариант 15 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 11.55 | 10 | 2.5 |
| 2 | 432 | 11 | 208 |
| 3 | 0.014 | 12 |  |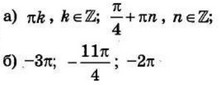
| 4 | 0.06 | 13 |  |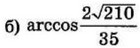
| 5 | -9 | 14 | (-1; 0) |
| 6 | 0.25 | 15 | 16 |
| 7 | 2 | 16 | б) 6 |
| 8 | 0.32 | 17 |  |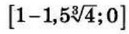
| 9 | 3 | 18 | а) да; б) нет; в) 26 |
| Вариант 16 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 12 | 10 | -15 |
| 2 | 192 | 11 | 5 |
| 3 | 0.29 | 12 |  |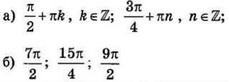
| 4 | 0.02 | 13 |  |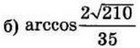
| 5 | -8 | 14 | (-∞; -0.5) |
| 6 | 0.125 | 15 | 19 |
| 7 | 4 | 16 | б) 8 |
| 8 | 1.16 | 17 |  |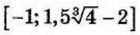
| 9 | 1 | 18 | а) да; б) нет; в) 80 |
| Вариант 17 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 10 | 10 | 16 |
| 2 | 80 | 11 | -24 |
| 3 | 0.08 | 12 |  |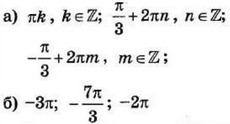
| 4 | 0.2 | 13 | б) 45° |
| 5 | -2.5 | 14 |  |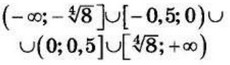
| 6 | 216 | 15 | 29 |
| 7 | -2 | 16 | б) 5/3 |
| 8 | 175 | 17 | -1/2; 2 |
| 9 | 18 | 18 | а) нет; б) да; в) 306 |
| Вариант 18 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 35 | 10 | 2.25 |
| 2 | 10 | 11 | -15 |
| 3 | 0.2 | 12 |  |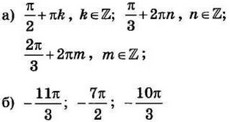
| 4 | 0.24 | 13 | б) arctg 0.5 |
| 5 | -0.2 | 14 |  |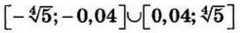
| 6 | 3.5 | 15 | 24 |
| 7 | 28 | 16 | б) 2.4 |
| 8 | 43.75 | 17 | 1; 9 |
| 9 | 21 | 18 | а) нет; б) да; в) 552 |
| Вариант 19 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2.5 | 10 | 2 |
| 2 | 7.28 | 11 | -34 |
| 3 | 0.25 | 12 |  |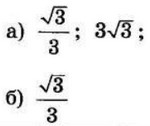
| 4 | 0.22 | 13 | б) 0.3√30 |
| 5 | -1.5 | 14 | (-∞; -1] ∪ [2; +∞) |
| 6 | 1 | 15 | 1300 тыс. рублей |
| 7 | 0.2 | 16 | б) 71° |
| 8 | 115 | 17 |  |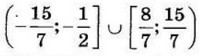
| 9 | 135 | 18 |  |
| Вариант 20 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 10 | 27 |
| 2 | 7.68 | 11 | 0 |
| 3 | 0.75 | 12 |  |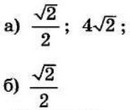
| 4 | 0.27 | 13 | б) arctg 2 |
| 5 | -4.5 | 14 | [-5; 0) ∪ (0; 2.5] |
| 6 | 10 | 15 | 2541 тыс. рублей |
| 7 | -0.25 | 16 |  |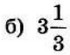
| 8 | 220 | 17 |  |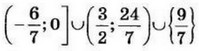
| 9 | 52 | 18 | а) 42; б) положительных; в) 24 |
| Вариант 21 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 113 | 10 | 15 |
| 2 | 60 | 11 | 7 |
| 3 | 0.2 | 12 |  |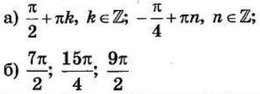
| 4 | 0.973 | 13 |  |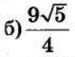
| 5 | 5.5 | 14 |  |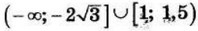
| 6 | 324 | 15 | 500 тыс. рублей |
| 7 | 2 | 16 | б) 4.8 |
| 8 | 6250 | 17 |  |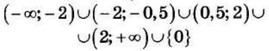
| 9 | 14 | 18 |  |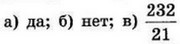
| Вариант 22 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.75 | 10 | 3.4 |
| 2 | 45 | 11 | 1.2 |
| 3 | 0.3 | 12 |  |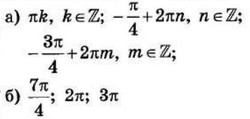
| 4 | 0.9744 | 13 |  |
| 5 | 11 | 14 |  |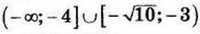
| 6 | -7.5 | 15 | 20 |
| 7 | 7 | 16 | б) 7.5 |
| 8 | 1.3 | 17 | [1; 9) |
| 9 | 5 | 18 | а) да; б) нет; в) 10 |
| Вариант 23 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 62 | 10 | 28 |
| 2 | 25 | 11 | 18 |
| 3 | 0.25 | 12 |  |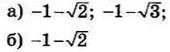
| 4 | 0.3 | 13 |  |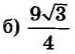
| 5 | -2 | 14 | (-∞; -1) ∪ {0} ∪ (0.5; +∞) |
| 6 | 80 | 15 | 35 700 рублей |
| 7 | 6 | 16 |  |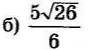
| 8 | 60 | 17 |  |
| 9 | 75 | 18 | а) 7; б) 15; в) 14 |
| Вариант 24 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 78 | 10 | -28 |
| 2 | 20 | 11 | -2 |
| 3 | 0.2 | 12 |  |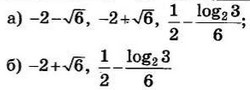
| 4 | 0.82 | 13 |  |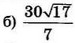
| 5 | 0 | 14 |  |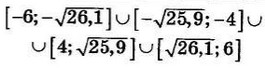
| 6 | 28 | 15 | 53 820 рублей |
| 7 | 6 | 16 |  |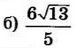
| 8 | 30 | 17 |  |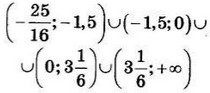
| 9 | 10 | 18 | а) 12; б) 15; в) 6 |
| Вариант 25 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 37 | 10 | -0.4 |
| 2 | 135 | 11 | 14 |
| 3 | 0.18 | 12 |  |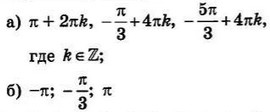
| 4 | 3 | 13 | б) 36 |
| 5 | 0.8 | 14 |  |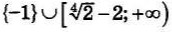
| 6 | 0.4 | 15 | 1 080 000 рублей |
| 7 | -0.2 | 16 |  |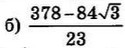
| 8 | 6 | 17 |  |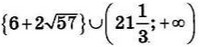
| 9 | 35 | 18 | а) нет; б) 21; в) 82 |
| Вариант 26 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 53 | 10 | -13 |
| 2 | 72 | 11 | 1 |
| 3 | 0.38 | 12 |  |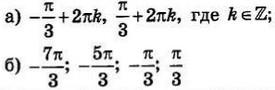
| 4 | 5 | 13 | б) 189 |
| 5 | -4 | 14 | (-0.5; 0.5) ∪ (0.5; 624.5) |
| 6 | -0.3 | 15 | 1 706 400 рублей |
| 7 | -0.75 | 16 | б) 91(5√2 — 7) |
| 8 | 96 | 17 |  |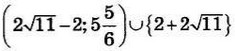
| 9 | 28 | 18 | а) нет; б) 36; в) 182 |
| Вариант 27 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 29 | 10 | 76 |
| 2 | 315 | 11 | -3 |
| 3 | 0.14 | 12 |  |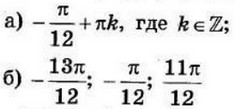
| 4 | 0.03 | 13 | б) 45° |
| 5 | 4 | 14 | (-1; 0) ∪ {log53} |
| 6 | 2.72 | 15 | 54 925 рублей |
| 7 | 6 | 16 | б) 8 |
| 8 | 7 | 17 | [0; 1.5) ∪ [2; +∞) |
| 9 | 77 | 18 | а) да; б) нет; в) 16 |
| Вариант 28 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 10 | -5 |
| 2 | 176 | 11 | 38 |
| 3 | 0.375 | 12 |  |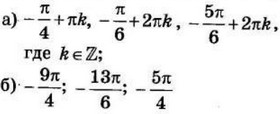
| 4 | 0.012 | 13 |  |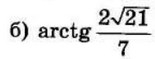
| 5 | -1 | 14 |  |
| 6 | -3 | 15 | 78 125 рублей |
| 7 | -3 | 16 | б) 18 |
| 8 | 28 | 17 |  |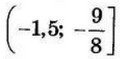
| 9 | 6 | 18 | а) да; б) нет; в) 12 |
| Вариант 29 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 60 | 10 | 67 |
| 2 | 18 | 11 | -21 |
| 3 | 0.24 | 12 |  |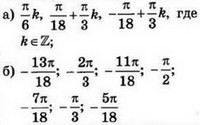
| 4 | 0.2 | 13 | б) 36 + 30√2 |
| 5 | 3 | 14 | [2; 5) |
| 6 | 4 | 15 | 126 694.4 рубля |
| 7 | 4 | 16 | б) 1 |
| 8 | 6.5 | 17 |  |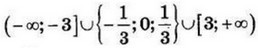
| 9 | 6.4 | 18 | а) да; б) нет; в) 2805 |
| Вариант 30 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 64 | 10 | 3 |
| 2 | 4 | 11 | -8 |
| 3 | 0.28 | 12 |  |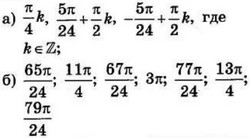
| 4 | 0.6 | 13 |  |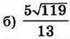
| 5 | 4 | 14 | (0; 5] |
| 6 | 8 | 15 | 1-й объект — 7 человек 2-й объект — 23 человека; 43 150 рублей |
| 7 | 14 | 16 | б) 50 |
| 8 | 9.6 | 17 | 4 < a ≤ 16 |
| 9 | 22 | 18 | а) да; б) нет; в) 2220 |
| Вариант 31 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6.5 | 10 | -7 |
| 2 | 54 | 11 | 8 |
| 3 | 0.98 | 12 |  |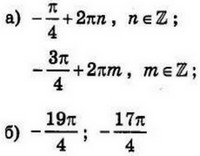
| 4 | 0.2 | 13 |  |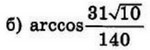
| 5 | 2 | 14 | [-2; 2) |
| 6 | -10 | 15 | 39 |
| 7 | 2 | 16 | б) 9√2 |
| 8 | 25 | 17 |  |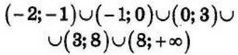
| 9 | 54 | 18 | а) нет; б) нет; в) 676 г. |
| Вариант 32 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 30 | 10 | 13 |
| 2 | 27 | 11 | -9 |
| 3 | 0.024 | 12 |  |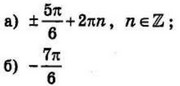
| 4 | 0.15 | 13 |  |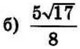
| 5 | -2 | 14 | (-2; 1) ∪ (1; 2) |
| 6 | 91 | 15 | 1.6 млн рублей |
| 7 | 3 | 16 | б) 27√3 |
| 8 | 17 | 17 |  |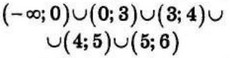
| 9 | 12 | 18 | а) нет; б) нет; в) 240 г |
| Вариант 33 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 72.5 | 10 | -2.5 |
| 2 | 47 | 11 | 26 |
| 3 | 0.28 | 12 |  |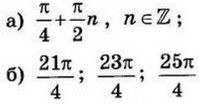
| 4 | 0.097 | 13 | б) 13√6 |
| 5 | -5 | 14 |  |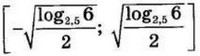
| 6 | 65 | 15 | 2.58 |
| 7 | 3 | 16 | б) 5 : 7 |
| 8 | 8 | 17 |  |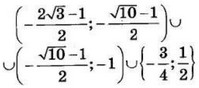
| 9 | 48 | 18 | а) нет; б) нет; в) 3 |
| Вариант 34 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 68 | 10 | -0.25 |
| 2 | 76 | 11 | -1 |
| 3 | 0.16 | 12 |  |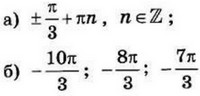
| 4 | 0.068 | 13 | б) 48.5 |
| 5 | 6 | 14 |  |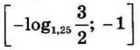
| 6 | 16 | 15 | 4.05 |
| 7 | 6 | 16 | б) 10 : 11 |
| 8 | 633 | 17 |  |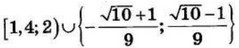
| 9 | 64 | 18 | а) да; б) нет; в) 5 |
| Вариант 35 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 21 | 10 | 0.75 |
| 2 | 200 | 11 | 9 |
| 3 | 0.56 | 12 |  |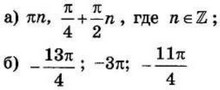
| 4 | 0.9 | 13 | б) 4√3 |
| 5 | -2 | 14 | [3 — √5; 2.8] ∪ [3.2; 3 + √5] |
| 6 | 7.5 | 15 | 20 |
| 7 | 0.5 | 16 | б) 1 : 3 : 1 |
| 8 | 0.31 | 17 | [-3; 22] |
| 9 | 20 | 18 | а) да; б) 180; в) 546 |
| Вариант 36 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 35 | 10 | -0.5 |
| 2 | 88 | 11 | 30 |
| 3 | 0.12 | 12 |  |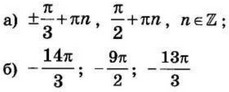
| 4 | 12 | 13 | б) 6√3 |
| 5 | -5 | 14 |  |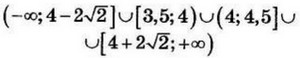
| 6 | 2.5 | 15 | 3 |
| 7 | 5.5 | 16 | б) 4 : 5 : 4 |
| 8 | 1.728 | 17 | (-∞; 4 — 2√2] ∪ ∪ [3.5; 4) ∪ ∪ (4; 4.5] ∪ ∪ [4 + 2√2; +∞) |
| 9 | 756 | 18 | а) да; б) 270; в) 17 |
Перейти к содержимому
ЕГЭ-2023. Сборник тренировочных вариантов. Книга предназначена для подготовки учащихся к ЕГЭ по математике. В сборнике представлены: 36 типовых экзаменационных вариантов, составленных в соответствии с демоверсиями КИМ ЕГЭ 2023 года; ответы ко всем заданиям и критерии оценивания.
Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться: