Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Спрятать решение
Решение.
Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких прямоугольников и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Примечание.
Площадь четырёхугольника, диагонали которого перпенликулярны, равна половине произведения диагоналей. Поэтому искомая площадь равна 4.
Каталог заданий
Версия для печати и копирования в MS Word
1
Задания Д4 № 244993
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 244993: 256851 256853 256855 256857 256859 256861 256863 256865 256867 256869 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Спрятать решение
Решение.
Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких прямоугольников и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Примечание.
Площадь четырёхугольника, диагонали которого перпенликулярны, равна половине произведения диагоналей. Поэтому искомая площадь равна 4.
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Спрятать решение
Решение.
Площадь четырёхугольника равна разности площади большого квадрата, одного маленького квадрата и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Задания Д4 № 256851
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 244993: 256851 256853 256855 256857 256859 256861 256863 256865 256867 256869 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Задания Д4 № 256851
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 244993: 256851 256853 256855 256857 256859 256861 256863 256865 256867 256869 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Целое положительное
число 256851
– составное число.
Сумма цифр: 27. Произведение цифр: 2400.
24 — количество делителей числа.
Обратным числом является 0.00000389330779323421.
Системы счисления:
двоичная система: 111110101101010011, троичная: 111001100000, восьмеричная: 765523, шестнадцатеричная: 3EB53.
В числе байт 256851 содержится 250 килобайтов 851 байт .
Число 256851 азбукой Морзе: ..— ….. -…. —.. ….. .—-
Косинус: 0.7852, тангенс: 0.7887, синус: 0.6193.
Натуральный логарифм числа 256851 равен 12.4563.
Десятичный логарифм числа равен 5.4097.
506.8047 — квадратный корень, 63.5663 — корень кубический.
Возведение числа в квадрат: 6.5972e+10.
Число секунд 256851 – это 2 дня 23 часа 20 минут 51 секунда .
Нумерологическое цифра числа 256851 — 9.
Задание 1
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Ответ: 5,5
Задание 2
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Ответ: 2048
Задание 3
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Ответ: 0,06
Задание 4
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,96. Вероятность того, что масса окажется больше, чем 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.
Ответ: 0,89
Задание 5
Найдите корень уравнения $$log_3(5-2x)=log_3(1-4x)+1$$
Ответ: -0,2
Задание 6
Найдите значение выражения $$frac{sin 126^{circ}}{4sin 63^{circ}cdot sin 27^{circ}}$$
Ответ: 0,5
Задание 7
На рисунке изображён график $$y=f'(x)$$ — производной функции $$f(x)$$, определённой на интервале $$(-2;20)$$. Найдите количество точек экстремума функции $$f(x)$$, принадлежащих отрезку $$[1;15]$$.
Ответ: 5
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,3122cdot 10^7$$ Па$$cdot$$м4, где $$p$$ — давление в газе в паскалях, $$V$$ — объём газа в в кубических метрах, $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в куб. м) будет занимать газ при давлении $$p$$, равном $$1,25cdot 10^6$$ Па.
Ответ: 5,832
Задание 9
Моторная лодка прошла против течения реки 96 км и вернулась в. пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
Задание 10
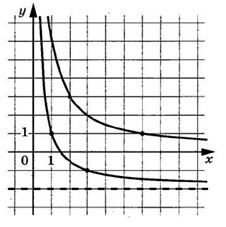
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Задание 11
Найдите наименьшее значение функции $$y=xsqrt{x}-27x+6$$ на отрезке $$[1;422]$$
Ответ: -2910
Задание 12
а) Решите уравнение $$2sin^{2}x-3cos(-x)-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$
Ответ: а)$$pi+2pi k; pmfrac{2pi}{3}+2pi n, n,k in Z$$ б)$$frac{8pi}{3};3pi; frac{10pi}{3}$$
Задание 13
В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ с большим основанием $$AD$$. Диагонали трапеции пересекаются в точке $$O$$. Точки $$M$$ и $$$$ — середины боковых сторон $$AB$$ и $$CD$$ соответственно. Плоскость $$alpha$$ проходит через точки $$M$$ и $$N$$ параллельно прямой $$SO$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ является трапецией.
б) Найдите площадь сечения пирамиды $$SABCD$$ плоскостью $$alpha$$, если $$AD=9$$, $$BC=7$$, $$SO=6$$, а прямая $$SO$$ перпендикулярна прямой $$AD$$.
Ответ: 24
Задание 14
Решите неравенство $$4^x+frac{112}{4^{x}-32}leq 0$$
Ответ: $$(-infty;1];[log_{4} 28;2,5)$$
Задание 15
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
— каждый январь долг будет возрастать на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— платежи в 2028 и 2029 годах должны быть равными;
— к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?
Ответ: 400 тыс. руб.
Задание 16
В параллелограмме $$ABCD$$ угол $$BAC$$ вдвое больше угла $$CAD$$. Биссектриса угла $$BAC$$ пересекает отрезок $$BC$$ в точке $$L$$. На продолжении стороны $$CD$$ за точку $$D$$ выбрана такая точка $$E$$, что $$AE=CE$$.
а) Докажите, что $$AL:AC=AB:BC$$.
б) Найдите $$EL$$, если $$AC=21$$, $$tgangle BCA=0,4$$.
Ответ: 14,2
Задание 17
Найдите все значения $$a$$, при каждом из которых уравнение $$(a-x)^2+4a+1=(2x+1)^2-8|x|$$ имеет четыре различных корня.
Ответ: (-4;-3);(-3;-1);(-1;0)
Задание 18
Есть три коробки: в первой коробке 112 камней, во второй — 99, а третья — пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй — 99, а в третьей — 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Ответ: а)да б)нет в)195
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
На экранах долгожданный шестой сезон одного из самых популярных и востребованных сериалов на зарубежном телевидении. Проект «Викинги» повествует о выдающемся воинственном народе, который проживает в Скандинавии и управляется безумным, яростным, но при этом очень мудрым правителем Рагнаром Лодброком. Этот человек смог собрать вокруг себя верных людей, смог установить свои правила на родных территориях, а вскоре отправился на покорение европейских земель. Главный герой повёл за собой свою армию, которая дошла с ним до территории Франции, осадив Париж и забрав сокровища одной из самых могущественных стран центральной Европы! Викингам по силам оказалось разбить армии англичан, которых не спасло даже нахождение на море. Ко всему прочему, главные персонажи сумели пробиться вглубь континента, наворотив дел и в других частях Европы.Продолжение истории обещает зрителям ещё более интересные походы. В этот раз главный герой вместе с верными товарищами отправится на восточные земли. Его встреча с Вещим Олегом, роль которого исполнит великолепный российский актёр Данила Козловский будет судьбоносной. Но чем же обернётся новый сезон знаменитого сериала?
- Название: Vikings
- Год выхода: 2013-03-03
- Страна: Канада, Ирландия
- Режиссер: Киаран Доннелли, Кен Джиротти, Стивен Ст.
- Статус сериала: Завершен
- Перевод: LostFilm
- Качество: FHD (1080p) (45 мин)
- Возраст: Сериал для зрителей старше 18+ лет
-
8.2
8.5
- В главных ролях: Кэтрин Уинник, Густаф Скарсгард, Александр Людвиг, Джорджия Хёрст, Алекс Хег Андерсен, Джордан Патрик Смит, Марко Ильсё, Петер Францен, Трэвис Фиммел, Клайв Стэнден
- Жанры: Приключения, Военный, Исторический, Боевик, Мелодрама, Драма
6 сезон 21 серия
Викинги смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет
К сожалению некоторые диалоги в сериале не переведены, рекомендуем в настройках включить субтитры, чтобы понимать диалоги. Приятного просмотра!
Свойства натурального числа 244993, 0x03BD01, 0x3BD01:
Рейтинг 0 из 10,
оценок: 0.
Системы счисления, перевод в систему счисления
Десятичное число 244993
-
- 244993 в шестнадцатеричной системе счисления
- 3BD01
-
- 244993 в двоичной системе счисления
- 111011110100000001
-
- 244993 в восьмеричной системе счисления
- 736401
Шестнадцатеричное число 3BD01
-
- 3BD01 в десятичной системе
- 244993
-
- 3BD01 в двоичной системе
- 111011110100000001
-
- 3BD01 в восьмеричной системе
- 736401
Двоичное число 111011110100000001
-
- 111011110100000001 в десятичной системе
- 244993
-
- 111011110100000001 в шестнадцатеричной системе
- 3BD01
-
- 111011110100000001 в восьмеричной системе
- 736401
Восьмеричное число 736401
-
- 736401 в десятичной системе
- 244993
-
- 736401 в шестнадцатеричной системе
- 3BD01
-
- 736401 в двоичной системе
- 111011110100000001
Основные арифметические и алгебраические свойства
-
- Число 244993 на русском языке, number in Russian, число 244993 прописью:
- двести сорок четыре тысячи девятьсот девяносто три
-
- Четность
- Нечетное число 244993
-
- Разложение на множители, делители числа 244993
- 7, 31, 1129, 1
-
- Простое или составное число
- Составное число 244993
-
- Числа делящиеся на целое число 244993
- 489986, 734979, 979972, 1224965, 1469958, 1714951, 1959944, 2204937
-
- Число 244993 умноженное на число два
- 489986
-
- 244993 деленное на число 2
- 122496.5
-
- Список 8-ми простых чисел перед числом
- 244957, 244943, 244939, 244901, 244897, 244889, 244877, 244873
-
- Сумма десятичных цифр
- 31
-
- Количество цифр
- 6
-
- Десятичный логарифм 244993
- 5.3891536757735
-
- Натуральный логарифм 244993
- 12.40898491769
-
- Это число Фибоначчи?
- Нет
-
- Число на 1 больше числа 244993,
следующее число - число 244994
- Число на 1 больше числа 244993,
-
- Число на 1 меньше числа 244993,
предыдущее число - 244992
- Число на 1 меньше числа 244993,
Степени числа, корни
-
- 244993 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 60021570049
- 244993 во второй степени (в квадрате)
-
- В третьей степени (в кубе, 244993 в степени 3, x³) равно
- 14704864511014657
-
- Корень квадратный из 244993
- 494.96767571226
-
- Корень кубический из числа 244993 =
- 62.572651515394
Тригонометрические функции, тригонометрия
-
- Синус, sin 244993 градусов, sin 244993°
- -0.2249510543
-
- Косинус, cos 244993 градусов, cos 244993°
- -0.9743700648
-
- Тангенс, tg 244993 градусов, tg 244993°
- 0.2308681911
-
- Синус, sin 244993 радиан
- -0.82004952221314
-
- Косинус, cos 244993 радиан
- 0.57229256601672
-
- Тангенс, tg 244993 радиан равно
- -1.4329201022492
-
- 244993 градуса, 244993° =
- 4275.9344943385 радиан
-
- 244993 радиан =
- 14037064.910249 градуса, 14037064.910249°
Контрольные суммы, хэши, криптография
-
- MD-5 хэш(244993)
- 342701859b13f7e9377a20abf214ab23
-
- CRC-32, CRC32(244993)
- 1232487430
-
- SHA-256 hash, SHA256(244993)
- d8b9407e07dc66708ff1a0e88c6375e38dcfe24b6743ad4e6cd05a7c19ebfe55
-
- SHA1, SHA-1(244993)
- 0cfcb7f720848967164b5f222a138bdf95e62d05
-
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(244993)
- 35e0d55e92aabc3201082b483a956f4ccd0ef29236e8d20db89c156e9d5d65a9
-
- Base64
- MjQ0OTkz
Языки программирования
-
- C++, CPP, C значение 244993
- 0x03BD01, 0x3BD01
-
- Delphi, Pascal значение числа 244993
- $03BD01
Дата и время
-
- Конвертация UNIX timestamp 244993 в дату и время
-
- UTC
- суббота, 3 января 1970 г., 20:03:13 GMT
- в Москве, Россия
- суббота, 3 января 1970 г., 23:03:13 Московское стандартное время
- в Лондоне, Великобритания
- суббота, 3 января 1970 г., 21:03:13 GMT+01:00
- в Нью-Йорке, США
- суббота, 3 января 1970 г., 15:03:13 Восточно-американское стандартное время
Интернет
-
- Конвертация в IPv4 адрес Интернет
- 0.3.189.1
-
- 244993 в Википедии:
- 244993
Другие свойства числа
-
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/244993
-
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x3BD01
-
- Номер телефона
- 24-49-93
Цвет по числу 244993, цветовая гамма
-
- html RGB цвет 244993, 16-ричное значение
- #03BD01 — (3, 189, 1)
-
- HTML CSS код цвета #03BD01
- .color-mn { color: #03BD01; }
.color-bg { background-color: #03BD01; }
Цвет для данного числа 244993
Здесь вы можете изменить составляющую цвета для данного числа 244993 или цвета 03BD01:
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-26

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!