Решу егэ математика 25621

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Спрятать решение

Решение.

Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

Ответ: 94.

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней данного многогранника, и смиритесь:

=94.

Спрятать решение

Курс Д. Д. Гущина

Гость 17.10.2012 13:24

объясните, пожалуйста, почему в ответе идет полная площадь поверхности многогранника? ведь в нем же есть вырезанный кусок!

Гость

Вырезанный кусок меняет объём, но не меняет площади многогранника.

Гость 01.06.2013 13:20

а как вы так решили??? объясните что это за сумма произведений? откуда вы берете ее?

Александр Иванов

2*3*5 — это площадь всех(двух) горизонтальных поверхностей, аналогично остальные два произведения

Гость 02.06.2013 16:17

почему не меняет? представим, что нам надо наклеить на этот многогранник обои. мы же будем клеить на все стороны, открытые взору — получается, что площадь поверхности увеличивается

Александр Иванов

Хороший пример с обоями. У Вас, например, передняя грань из-за выреза уменьшилась на 2, но появилась новая маленькая грань, точно такой же площади, так что обоев потратиться ровно столько же.

Источник

Практикум по теме «Площадь поверхности составного многогранника»
15 января 2020 г. 11 класс

Цель: практическое закрепление ЗУН.

Задачи из открытого банка задач.

1. Задание 8 № 25541

Найдите площадь поверхности
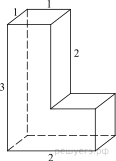
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей
прямоугольников со сторонами 2, 1:

Ответ: 18.

2. Задание 8 № 25561

Найдите площадь
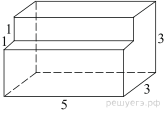
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей
квадратов со стороной 1:

Ответ: 76.

3. Задание 8 № 25581

Найдите площадь поверхности
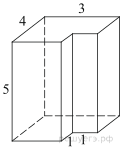
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух
квадратов со стороной 1:

Ответ: 92.

4. Задание 8 № 25601

Найдите площадь
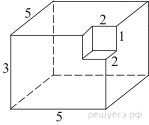
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:

Ответ: 110.

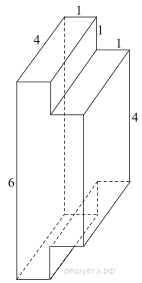
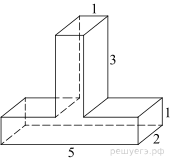
5. Задание 8 № 25621

Найдите площадь
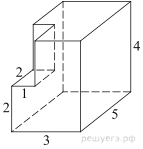
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

Ответ: 94.

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней
данного многогранника, и смиритесь:

6. Задание 8 № 25641

Найдите площадь
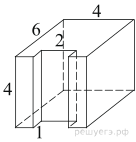
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 6, 4, 4 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 2:

Ответ: 132.

7. Задание 8 № 25661

Найдите площадь
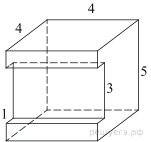
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 4, 4, 5 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 3:

Ответ: 114.

8. Задание 8 № 25681

Найдите площадь поверхности
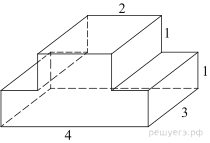
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
прямоугольников со сторонами 1, 3, 4 и 1, 2, 3, уменьшенной на удвоенную
площадь прямоугольника со сторонами 2, 3:

Ответ: 48.

9. Задание 8 № 25701

Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь
квадрата стороной 4:

Ответ: 84.

Приведем другое решение

Площадь поверхности заданного многогранника равна площади
прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади
квадратов со стороной 1:

10. Задание 8 № 25721

Найдите площадь
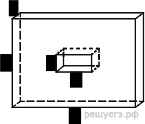
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной
на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького
параллелепипеда, излишне учтенной при расчете площадей поверхности
параллелепипедов:

Ответ: 96.

11. Задание 8 № 25881

Найдите площадь
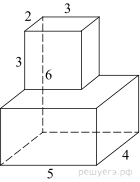
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов со сторонами 2, 3, 3 и 5, 4, 3 уменьшенной на удвоенную
площадь прямоугольника со сторонами 3, 2:

Ответ: 124.

12. Задание 8 № 27071

Найдите площадь
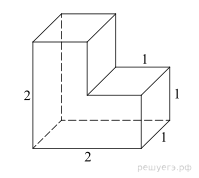
поверхности многогранника, изображенного на рисунке, все двугранные углы
которого прямые.

Решение.

Площадь поверхности заданного многогранника складывается из
четырех площадей квадратов со стороной 1, двух прямоугольников со сторонами 1 и
2 и двух граней (передней и задней), площади которых в свою очередь
складываются из трех единичных квадратов каждая. Всего 4 + 4 + 6 = 14.

Ответ: 14.

13. Задание 8 № 27158

Найдите площадь
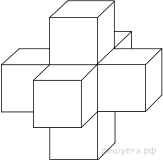
поверхности пространственного креста, изображенного на рисунке и составленного
из единичных кубов.

Решение.

Поверхности креста составлена из шести поверхностей кубов, у
каждого из которых отсутствует одна грань. Тем самым, поверхность креста
состоит из 30 единичных квадратов, поэтому ее площадь равна 30.

Ответ: 30.

14. Задание 8 № 77155

Найдите площадь
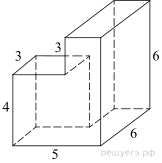
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника равна сумме площадей
поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4,
уменьшенной на две площади прямоугольников со сторонами 3 и 4:

Ответ: 162.

15. Задание 8 № 77156

Найдите площадь
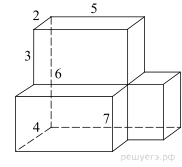
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих ее параллелепипедов с ребрами 2, 5, 6; 2, 5, 3 и 2, 2,
3, уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:

Ответ: 156.

16. Задание 8 № 77157

Найдите площадь
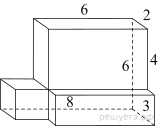
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих его параллелепипедов с измерениями 2, 4, 6; 1, 6, 2 и 2, 2, 2:

Ответ: 152.

17. Задание 8 № 512330

Найдите площадь
поверхности многогранника, изображённого на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника складывается из площадей
двух параллелепипедов со сторонами 1, 3, 2 и 1, 2, 5 за вычетом двух площадей
прямоугольников со сторонами 2 и 1, которые учитываются дважды в представленном
многограннике:

Ответ: 52

Источник


3505	а) Решите уравнение 2^(5sin(5x))+6^(1+sin(5x))=24^(sin(5x))+3*8^(1/3+sin(5x)) б) Найдите все корни этого уравнения, принадлежащие отрезку [(5pi)/2; (7pi)/2]. Решение График	а) Решите уравнение 2^5sin5x +6^ 1+sin5x = 24^sin5x +3 8^1/3+sin5x ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 12

3503	Решите неравенство: ((log_{3}(x-1.5))^2-1) / (2^x-3)<= 0 Решение График	Решите неравенство: log2 3 (x-1,5)^2 -1) / 2^x -3) <= 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 14

3498	Решите уравнение cos((pi(2x-6))/6)=sqrt(3)/2. В ответе запишите наибольший отрицательный корень Решение График	Решите уравнение cos(pi(2x-6) /6) = корень из 3 /2. В ответе запишите наибольший отрицательный корень ! 36 вариантов ФИПИ Ященко 2023 Вариант 3 Задание 5

3494	а) Решите уравнение 4^(x+sqrt(x)-1.5)+3*4^(x-sqrt(x)+1.5)-4^(x+1)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [2; 6] Решение График	а) Решите уравнение 4^(x+sqrt(x) -1.5) +3*4^(x-sqrt(x)+1.5) -4^(x+1) =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 3 Задание 12

3493	Решите неравенство log_{tan(3.2)}(log_{3}(9-x^2))>= 0 Решение График	Решите неравенство log tg3,2 (log3 (9 -x^2)) >= 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 3 Задание 14

3480	а) Решите уравнение 2sin^2(x)-3cos(-x)-3=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [2pi; (7pi)/2]. Решение График	а) Решите уравнение 2sin2 x -3cos(-x) -3 =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 12

3478	Решите неравенство 4^x+112/(4^x-32)<= 0 Решение График	Решите неравенство 4^x +112 / 4^x-32 <= 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 14

3223	а) Решите уравнение sin^2(x/4+pi/4)sin^2(x/4-pi/4). =0.375sin^2(-pi/4). б) Найдите все корни этого уравнения, принадлежащие отрезку [-3pi; pi]. Решение График	а) Решите уравнение sin2 (x/4+pi/4) sin2(x/4-pi/4) = 0,375 sin2(-pi/4) ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 12

3222	Решите неравенство (50.2^(x+0.5)-0.25^(x+0.5)). *(0.5log_{0.2}^2(x+0.5)-2log_{5}(x+0.5)) > 0. Решение График	Решите неравенство (5 0.2 x+0,5 -0,2 5 x+0.5) (0.5log2 0,2 (x+0,5) -2log 5 (x+0.5)) > 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 14 🔥

3187	а) Решите уравнение cos(2x)-sqrt(2)cos((3pi)/2+x)-1=0 б) Укажите корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi]. Решение График	а) Решите уравнение cos2x -корень из 2 cos(3pi /2+ x) -1 =0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 12 Задание 12

Показана страница 3 из 5

Contains([ Условие задачи], ‘решите’)

Clear

Hide

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Решу егэ математика 25621

Задание 5 № 25621

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней данного многогранника, и смиритесь:

Задание 5 № 25621

Задание 5 25621.

Ege. sdamgia. ru

20.07.2018 22:35:15

2018-07-20 22:35:15

Источники:

Https://ege. sdamgia. ru/problem? id=25621

ЕГЭ–2022, физика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 25621

—>

Задание 2 № 25621

Даны следующие зависимости величин:

А) Зависимость модуля скорости тела от времени при прямолинейном равноускоренном движении с ненулевой начальной скоростью;

Б) Зависимость объема идеального газа от температуры при изобарном процессе;

В) зависимость энергии заряженного конденсатора от времени при гармонических колебаниях в колебательном контуре.

Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1−5. Для каждой зависимости А−В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами.

Ответ:

А) Зависимость модуля скорости тела от времени при прямолинейном равноускоренном движении выражается формулой Данная зависимость линейная, графиком которой является (2).

Б) Зависимость объема идеального газа от температуры при изобарном процессе прямая пропорциональная. Графиком такой зависимости является прямая линия, у которой начало не проходит через начало координат, т. к. абсолютный ноль не достижим, а при температуре близкой к абсолютному нулю вещество находится в твердом состоянии. Графиком такой зависимости является (4).

В) зависимость энергии заряженного конденсатора от времени при гармонических колебаниях в колебательном контуре выражается формулой причем колебания заряда происходят по закону Поэтому графиком такой зависимости является (5).

—>

Задание 2 № 25621

Для каждой зависимости А В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами.

Phys-ege. sdamgia. ru

28.04.2019 9:32:27

2019-04-28 09:32:27

Источники:

Https://phys-ege. sdamgia. ru/problem? id=25621

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 25621

Решу егэ математика 25621

Задание 5 № 25623

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 4:

Примечание: мы не ЗАБЫЛИ вычесть «площадь вырезанной части», мы знаем, что этого делать не нужно

Но вы же не вычли площадь маленького, который вырезан

Площадь поверхности выреза полностью дополняет фигуру до площади поверхности параллелепипеда.

Решение не правильно, так как вы не вычли площадь маленького, а вы просто нашли всю площадь поверхности большого многогранника. ОБРАТИТЕ ВНИМАНИЕ НА ЭТО ЗАДАНИЕ! ПОЖАЛУЙСТА

ОБРАТИТЕ ВНИМАНИЕ НА НАШЕ РЕШЕНИЕ! ПОЖАЛУЙСТА!

Площадь поверхности параллелепипеда с таким вырезом или без него ОДИНАКОВА

Почему мы берем полного многогранника а не фигуры?

Площади их поверхностей равны

Задание 5 № 25625

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

94 — это площадь поверхности целой фигуры, если мы её достроим и узнаем площадь, а потом нам нужно отнять площадь маленькой фигурки: 94-10=84

Добрый вечер! Отнимать ничего не нужно, поскольку рассматривается не объём а площадь поверхности. Площадь «кусочка», который якобы нужно отнять, полностью достраивает нам фигуру до прямоугольного параллелепипеда.

Задание 5 № 25629

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5:

Задание 5 № 513678

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности этого многогранника такая же, как площадь поверхности «целого» прямоугольного параллелепипеда, она равна удвоенной сумме попарных произведение его измерений: 2 · (3 · 5 + 5 · 5 + 5 · 3) = 110.

Здравствуйте, объясните пожалуйста, почему не вычитается отрезанный кусок многогранника?

Обратите внимание, что вырез тоже имеет свою площадь поверхности. Эта площадь поверхности равна той, если бы у нас был целый параллелепипед (можете мысленно части выреза перенести «на место» для построения полного параллелепипеда).

Задание 5 № 513708

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности этого многогранника такая же, как площадь поверхности «целого» прямоугольного параллелепипеда, она равна удвоенной сумме попарных произведений его измерений: 2 · (3 · 5 + 4 · 5 + 4 · 3) = 94.

Могу ошибаться. Нам же надо вычесть площадь «пустого» параллелепипида

Такие вопросы нам задают десятками. Читайте решение внимательно.

Задание 5 № 25627

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Это задание ещё не решено, приводим решение прототипа.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней данного многогранника, и смиритесь:

Задание 5 № 25625

Задание 5 № 513678

Но вы же не вычли площадь маленького, который вырезан.

Ege. sdamgia. ru

24.07.2017 6:01:08

2017-07-24 06:01:08

Источники:

Https://ege. sdamgia. ru/test? likes=25621

Источник

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

$a$ — старший коэффициент;
$b$ — средний коэффициент;
$c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0 х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение полного квадратного уравнения

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $3³

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

найти общий знаменатель дробей, входящих в уравнение;
умножить обе части уравнения на общий знаменатель;
решить получившееся целое уравнение;
исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

${3х-5}/{-2}={1}/{х}$

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х (3х — 5) = -2$

Раскроем скобки и соберем все слагаемые в левой части уравнения

$3х^2- 5х + 2 = 0$

Решим данное квадратное уравнение первым устным способом, т.к.

$a + b + c = 0$

$x_1 = 1, x_2 = {2}/{3}$

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1 = 1, x_2 = {2}/{3}$

Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.

Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.

Например,

${2}/{x}+5x=7$ – рациональное уравнение

$3x+√x=7$ — иррациональное уравнение (содержит корень)

Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
Найти общий знаменатель дробей, входящих в уравнение;
Умножить обе части уравнения на общий знаменатель;
Решить получившееся целое уравнение;
Исключить из его корней те, которые обращают в ноль общий знаменатель.

Решить уравнение: $4x+1-{3}/{x}=0$

Решение:

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x ≠ 0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x+1-{3}/{x}=0|·x$

$4x·x+1·x-{3·x}/{x}=0$

3. решаем полученное уравнение

$4x^2+x-3=0$

Решим вторым устным способом, т.к. $а+с=b$

Тогда, $x_1=-1, x_2=-{3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю

Ответ: $x_1=-1, x_2=-{3}/{4}$

При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$

Решить уравнение ${3x-5}/{-2}={1}/{x}$

Решение:

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х(3х-5)=-2$

Раскроем скобки и соберем все слагаемые в левой стороне

$3х^2-5х+2=0$

Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$

$x_1=1, x_2={2}/{3}$

В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=1, x_2={2}/{3}$

Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.

Чтобы решить иррациональное уравнение, необходимо:

Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
Решить полученное рациональное уравнение.
Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.

Решение:

Обе части уравнение возведем в квадрат:

$√{4х-3}^2=х^2$

Получаем квадратное уравнение:

$4х-3=х^2$

Перенесем все слагаемые в левую часть уравнения:

${-х}^2+4х-3=0$

Решим данное квадратное уравнение устным способом, так как

$a+b+c=0$

$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$√{4·1-3}=1$

$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.

$√{4·(3)-3}=3$

$√9=3$

$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит

$х_1=1$ наименьший корень.

Ответ: $1$

Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$

Решить уравнение: $х-6=√{8-х}$

Возведем обе части уравнения в квадрат

$(х-6)^2=8-х$

В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение

$х^2-2·6·х+6^2=8-х$

$х^2-12х+36=8-х$

Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.

$х^2-12х+36-8+х=0$

Приводим подобные слагаемые:

$х^2-11х+28=0$

Найдем корни уравнения через дискриминант:

$D=b^2-4ac=121-4·28=121-112=9=3^2$

$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$

$x_1=7; x_2=4$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$x_1=7$

$7-6=√{8-7}$

$1=1$, получили верное равенство, следовательно, корень нам подходит.

$x_2=4$

$4-6=√{8-4}$

$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.

Ответ: $7$

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n⋅a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.

Решить уравнение $25·5^х=1$

Решение:

В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$

$5^2·5^х=5^0$

При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются

$5^{2+х}=5^0$

Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели

$2+х=0$

$х=-2$

Ответ: $-2$

Решить уравнение $2^{3х+2}-2^{3х-2}=30$

Решение:

Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель

$2^{3x+2}-2^{3x-2}=30$

$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$

$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$

$2^{3x-2}(2^4-1)=30$

$2^{3x-2}·15=30$

Разделим обе части уравнения на $15$

$2^{3х-2}=2$

$2^{3х-2}=2^1$

$3х-2=1$

$3х=3$

$х=1$

Ответ: $1$

Источник