Решу егэ математика 25701 - Помощь в подготовке к экзаменам и поступлению

Задания

Версия для печати и копирования в MS Word

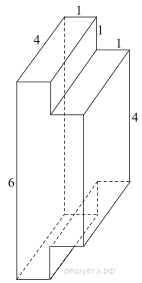
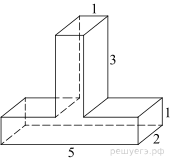
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Спрятать решение

Решение.

Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4:

Ответ: 84.

Приведем другое решение

Площадь поверхности заданного многогранника равна площади прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади квадратов со стороной 1:

Источник

Практикум по теме «Площадь поверхности составного многогранника»
15 января 2020 г. 11 класс

Цель: практическое закрепление ЗУН.

Задачи из открытого банка задач.

1. Задание 8 № 25541

Найдите площадь поверхности
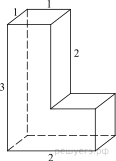
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей
прямоугольников со сторонами 2, 1:

Ответ: 18.

2. Задание 8 № 25561

Найдите площадь
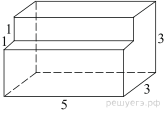
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей
квадратов со стороной 1:

Ответ: 76.

3. Задание 8 № 25581

Найдите площадь поверхности
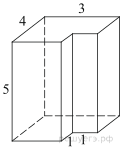
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух
квадратов со стороной 1:

Ответ: 92.

4. Задание 8 № 25601

Найдите площадь
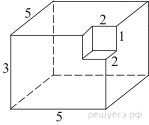
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:

Ответ: 110.

5. Задание 8 № 25621

Найдите площадь
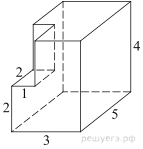
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

Ответ: 94.

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней
данного многогранника, и смиритесь:

6. Задание 8 № 25641

Найдите площадь
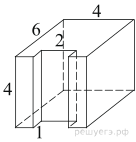
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 6, 4, 4 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 2:

Ответ: 132.

7. Задание 8 № 25661

Найдите площадь
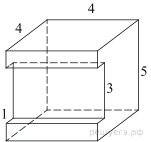
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 4, 4, 5 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 3:

Ответ: 114.

8. Задание 8 № 25681

Найдите площадь поверхности
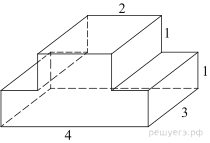
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
прямоугольников со сторонами 1, 3, 4 и 1, 2, 3, уменьшенной на удвоенную
площадь прямоугольника со сторонами 2, 3:

Ответ: 48.

9. Задание 8 № 25701

Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь
квадрата стороной 4:

Ответ: 84.

Приведем другое решение

Площадь поверхности заданного многогранника равна площади
прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади
квадратов со стороной 1:

10. Задание 8 № 25721

Найдите площадь
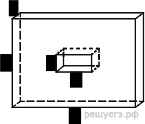
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной
на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького
параллелепипеда, излишне учтенной при расчете площадей поверхности
параллелепипедов:

Ответ: 96.

11. Задание 8 № 25881

Найдите площадь
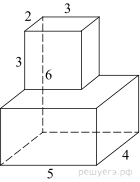
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов со сторонами 2, 3, 3 и 5, 4, 3 уменьшенной на удвоенную
площадь прямоугольника со сторонами 3, 2:

Ответ: 124.

12. Задание 8 № 27071

Найдите площадь
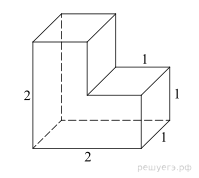
поверхности многогранника, изображенного на рисунке, все двугранные углы
которого прямые.

Решение.

Площадь поверхности заданного многогранника складывается из
четырех площадей квадратов со стороной 1, двух прямоугольников со сторонами 1 и
2 и двух граней (передней и задней), площади которых в свою очередь
складываются из трех единичных квадратов каждая. Всего 4 + 4 + 6 = 14.

Ответ: 14.

13. Задание 8 № 27158

Найдите площадь
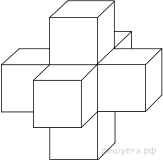
поверхности пространственного креста, изображенного на рисунке и составленного
из единичных кубов.

Решение.

Поверхности креста составлена из шести поверхностей кубов, у
каждого из которых отсутствует одна грань. Тем самым, поверхность креста
состоит из 30 единичных квадратов, поэтому ее площадь равна 30.

Ответ: 30.

14. Задание 8 № 77155

Найдите площадь
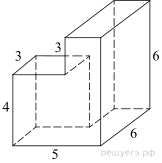
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника равна сумме площадей
поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4,
уменьшенной на две площади прямоугольников со сторонами 3 и 4:

Ответ: 162.

15. Задание 8 № 77156

Найдите площадь
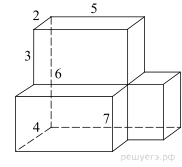
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих ее параллелепипедов с ребрами 2, 5, 6; 2, 5, 3 и 2, 2,
3, уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:

Ответ: 156.

16. Задание 8 № 77157

Найдите площадь
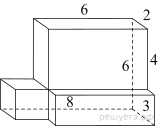
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих его параллелепипедов с измерениями 2, 4, 6; 1, 6, 2 и 2, 2, 2:

Ответ: 152.

17. Задание 8 № 512330

Найдите площадь
поверхности многогранника, изображённого на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника складывается из площадей
двух параллелепипедов со сторонами 1, 3, 2 и 1, 2, 5 за вычетом двух площадей
прямоугольников со сторонами 2 и 1, которые учитываются дважды в представленном
многограннике:

Ответ: 52

Источник

ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Отзывов (8)

adam

2013-05-05 в 19:08

Как нарисовать на отдельном листе все грани? Вообще не понимаю… Помогите, пожалуйста.

Ответить
- Александр Крутицких
  
  2013-05-05 в 20:07
  
  Адам, каждый отдельный элемент (грань) стройте по указанным размерам на листе в клетку. Подсчитайте площадь каждой грани и сложите все площади.
  
  Ответить
- Александр Крутицких
  
  2013-05-05 в 20:10
  
  Ответить
Влад

2013-05-07 в 03:59

Почему-то Получается 102 😉

Ответ точно без опечатки?)

Ответить
- Александр Крутицких
  
  2013-05-07 в 10:28
  
  Влад, без опечатки. Верно решено.
  
  Ответить
Даннил

2013-05-22 в 23:27

у меня получилось 94, там не нужно площадь маленького вырезанного многогранника вычитать?

Ответить
- Александр Крутицких
  
  2013-05-23 в 07:12
  
  Не нужно, считается вся площадь поверхности.
  
  Ответить
- Ирина
  
  2014-10-28 в 15:40
  
  Даннил, для нахождения объема, ты бы вычитал из общего объема — объем маленького вырезанного многогранника, а для площади — точно не надо!
  
  Представь, что ты хочешь покрасить краской заданную фигуру — ты что вырезанную часть не будешь красить? Будешь! И на нее пойдет такой же расход краски (соответственно и такая же площадь), как и у вырезанного многогранника.
  
  Ответить

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

РубрикиРубрики
Задачи по номерам!

№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
МЕТКИ

БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник


3069	а) Решите уравнение 2sin^3(pi+x)=1/2cos(x-(3pi)/2) б) Найдите все корни уравнения, принадлежащие отрезку [-(7pi)/2; -(5pi)/2]. Решение График	а) Решите уравнение 2sin 3 (pi +x) =1/2 cos(x — 3/2 pi) ! 36 вариантов ФИПИ Ященко 2022 Вариант 1 Задание 12

3068	Решите неравенство (4^x-52^x)^2-20(4^x-52^x) <= 96 Решение График	Решите неравенство (4 x -5 2 x) 2 -20(4 x-5 2 x) <= 96 ! 36 вариантов ФИПИ Ященко 2022 Вариант 1 Задание 14

2859	Решите неравенство (25^x-45^x)^2+85^x < 2*25^x+15 Решение График	Решите неравенство (25 x -4 5 x) 2 + 8 5 x < 2 25 x + 15 ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 15 (15.3) # Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 2 Задание 14

2549	а) Решите уравнение sin^4(x/4)-cos^4(x/4)=cos(x-pi/2) б) Найдите все корни этого уравнения, принадлежащие отрезку [-(3pi)/2; pi]. Решение График	Решите уравнение sin^4(x/4) -cos^4(x/4) = cos(x-pi/2) ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 12 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 13

2548	Решите неравенство (20.5^(x+2)-0.52^(x+2)). (2log_{0.5)^2(x+2)-0.5log_{2}(x+2)) <= 0. Решение График	Решите неравенство (20.5^(x+2)- 0.52^(x+ 2)) (2log^2_{0.5)(x+2)- 0.5log_{2}(x+ 2)) <= 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 14 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 15

2543	Решите неравенство lg^4(x^2-26)^4-4lg^2(x^2-26)^2 <= 240. Решение График	Решите неравенство lg^4(x^2 -26)^4 -4lg^2(x^2 -26)^2 <= 240 ! 36 вариантов ФИПИ Ященко 2022 Вариант 14 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 4 Задание 15

2532	а) Решите уравнение (x^2+2x-1)(log_{2}(x^2-3)+log_{0.5}(sqrt(3)-x))=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-2.5; -1.5] Решение График	Решите уравнение (x^2+ 2x -1)(log_{2}(x^2 -3)+ log_{0.5}(sqrt(3) -x))=0 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 13

2531	Решите неравенство (4^(x-0.5)+1)/(9*4^x-16^(x+0.5)-2) <= 0.5 Решение График	Решите неравенство (4^(x-0,5)+ 1)/ (9*4^x-16^(x+0,5) -2) <= 0,5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 15

2524	Решите неравенство x^2*log_{243}(-x-3) >= log_{3}(x^2+6x+9) Решение График	Решите неравенство x^2* log_{243}(-x- 3) >= log_{3}(x^2+ 6x+9) ! 36 вариантов ФИПИ Ященко 2022 Вариант 12 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 2 Задание 15 # Задача-Аналог 2367

Источник