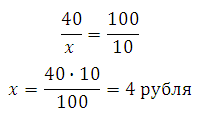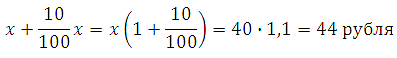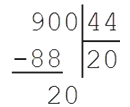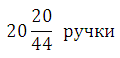Решу егэ математика 26619 - Помощь в подготовке к экзаменам и поступлению

Задания

Версия для печати и копирования в MS Word

Задания Д2 № 26619

Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

Спрятать решение

Решение.

После повышения цены ручка станет стоить 40 + 0,1 · 40  =  44 рубля. Разделим 900 на 44:

Значит, можно будет купить 20 ручек.

Ответ: 20.

Аналоги к заданию № 26619: 2487 25479 2489 2491 2493 2495 25431 25433 25435 25437 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.1.1 Целые числа, 1.1.3 Дроби, проценты, рациональные числа

Спрятать решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Источник

ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-08

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

РубрикиРубрики
Задачи по номерам!

№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
МЕТКИ

БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Дата: 2015-04-27

7695

Категория: ОкруглениеПроценты

Метка: №15-БАЗА

26619. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

Определим цену ручки после повышения на 10%. Для этого сначала найдём на какую сумму выросла цена. Обозначим её как х.

Составляем пропорцию: 40 рублей примем за 100% (величина с которой сравниваем), тогда х это 10%.

40 рублей — 100%

х рублей — 10%

Значит цена повысилась на 4 рубля, и ручка стала стоить 40+4=44 рубля.

Можно вычислить по формуле:

Теперь определим, какое число ручек можно купить на 900 рублей, разделим 900 на 44:

То есть, во время распродажи на 900 рублей можно купить:

Но часть ручки купить нельзя, поэтому результат округляем в меньшую сторону. Или его можно представить следующим образом: 900=20∙44+20.

То есть, на 900 рублей можно купить максимум 20 ручек по 44 рубля, причём сдача составит 20 рублей.

Ответ: 20

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Текстовые задачи ( B1 — B2)

В данном разделе решены все прототипы задания B1 ЕГЭ по математике. Условия заданий взяты с сайта mathege.ru. Кроме прототипов здесь размещены решения заданий B1 из различных сборников для подготовки к ЕГЭ по математике и из реальных вариантов ЕГЭ разных лет.

Задание B1 (№2443) (Прототип задания B1 № 26616)

Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?

Решение

60 : 7,2 = 8,33333…

Т.к. купить можно только целое число сырков, то на 60 рублей можно купить только 8 сырков (на 9 уже денег не хватит).

Ответ : 8

Прототип задания B1 (№26617)

Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?

Решение

Всего человек:

750+25 = 775.

Т.к. каждая спасательная шлюпка может вместить 70 человек, то:

775:70 = 11,07

и т.к. взять можно только целое число шлюпок, то всего потребуется 12 шлюпок.

Ответ: 12

Задание B1 (ЕГЭ 2013)

Одна таблетка лекарства весит 70 мг и содержит 4 % активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 1,05 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку в возрасте 5 месяцев и весом 8 кг в течение суток?

Решение

Найдем, сколько мг активного вещества содержится в одной таблетке:

(70 *4)/100 = 2,8 (мг).

Так как ребенок в возрасте до 6 месяцев, то ему полагается 1,05 мг активного вещества на каждый килограмм веса в сутки. Найдем, сколько нужно мг активного вещества ребенку весом 8 кг каждые сутки:

8*1,05 = 8,4 (мг).

Так как в одной таблетке содержится 0,28 мг активного вещества, то ребенку нужно дать

8,4 : 2,8 = 3 таблетки.

Ответ: 3

Задание B1 (ЕГЭ 2013)

Одна таблетка лекарства весит 20 мг и содержит 5 % активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 0,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку в возрасте трех месяцев и весом 5 кг в течение суток?

Решение

Найдем, сколько мг активного вещества содержится в одной таблетке:

(20 *5)/100 = 1 (мг).

Так как ребенок в возрасте до 6 месяцев, то ему полагается 0,4 мг активного вещества на каждый килограмм веса в сутки. Найдем, сколько нужно мг активного вещества ребенку весом 5 кг каждые сутки:

5*0,4 = 2 (мг).

Так как в одной таблетке содержится 1 мг активного вещества, то ребенку нужно дать

2 : 1 = 2 таблетки.

Ответ: 2

Прототип задания B1 (№26618)

Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?

Решение

Если скидка составляет 25%, то стоимость шампуня во время распродажи будет составлять 75 % от первоначальной цены. Тогда цена шампуня будет равна

(160*75)/100 = 160*0,75 = 120 (рублей).

1000/120 = 8,(3)

Т.е. во время распродажи можно купить 8 флаконов шампуня.

Ответ: 8.

Прототип задания B1 (№26619)

Решение

Найдем на сколько рублей повысилась цена: (40*10)/100 = 40*0,1 = 4 (рубля).

Значит новая цена ручки после повышения равна 40+4 = 44 рубля.

900/44 = 20,(45).

Значит, на 900 рублей после повышения цены можно будет купить 20 ручек.

Ответ: 20.

Прототип задания B1 (№26620)

Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?

Решение

Найдем, на сколько рублей понизилась цена: (40*10)/100 = 4 (рубля).

Новая стоимость тетради составит 40-4 = 36 рублей.

750/36 = 20,8(3).

Значит на 750 рублей после понижения цены можно купить 20 тетрадей.

Ответ: 20.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Источник

Яндекс Игры

Яндекс Игры — это набор самых прикольных и интересных онлайн игр от ведущей интернет-платформа компании «Яндекс». На данный момент насчитывается уже десятки тысяч игр разных жанров, от разных авторов, которые добавляют свои игры на эту платформу. Яндекс игры отличаются хорошей графикой, качеством звука, интересным игровым сюжетом, множеством функций, бонусов, достижениями и отсутствием глюков. Многие игры также имеют многопользовательский онлайн режим, где игроки с разных Городов могут играть совместно, перебивая рекорды друг друга и весело проводя время.

В нашем разделе Яндекс игр мы отобрали самые свежие и лучшие на наш взгляд игры, которые имеют систему прокачки, много уровней, интересный сюжет и многое другое. Такие игры несомненно заслуживают вашего внимания. Вы можете выбирать среди множества захватывающих игр различных жанров, таких как: Гонки, Шутеры, Кликеры, Бегалки, Бродилки, Хорроры, Выживание, а также среди игр на ловкость, логических, настольных и игр на внимание, а также известных игровых героев и персонажей. Благодаря регулярным обновлениям вы всегда сможете найти для себя что-нибудь интересное и весело провести свободное время, играя в одиночку или в компании друзей. Играйте и погрузитесь в огромный мир Яндекс игр прямо сейчас!

Источник