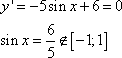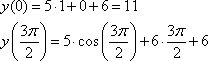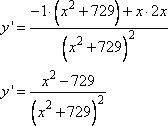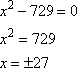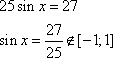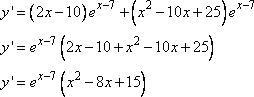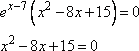Решу егэ математика 509612 - Помощь в подготовке к экзаменам и поступлению

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика базового уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Справочник

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Задания

Версия для печати и копирования в MS Word

Тип 17 № 509612

Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Спрятать решение

Решение.

Решим квадратное уравнение:

Ответ: −8.

Аналоги к заданию № 509612: 506842 510023 523099 523120 523163 525147 510185 510277 Все

Раздел кодификатора ФИПИ: Линейные, квадратные, кубические уравнения

Спрятать решение

Сообщить об ошибке · Помощь

О проекте · Редакция · Правовая информация · О рекламе

Источник

Задания

Версия для печати и копирования в MS Word

Известно, что a, b, c, и d  — попарно различные двузначные (положительные) числа.

а)  Может ли выполняться равенство

б)  Может ли дробь быть в 11 раз меньше, чем сумма

в)  Какое наименьшее значение может принимать дробь если и

Спрятать решение

Решение.

а)  Пусть и d=45. Тогда

б)  Предположим, что Тогда:

С другой стороны имеем: Следовательно, числа имеют разные знаки и не могут быть равны. Пришли к противоречию.

в)  Из условия следует, что и Значит, Используя неравенства и получаем:

Пусть и d=49. Тогда Следовательно, наименьшее возможное значение дроби равно

Ответ: а) Да, например, если и d=45; б) нет; в)

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты.	4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов.	3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов.	2
Верно получен один из следующий результатов: — обоснованное решение в п. а; — пример в п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	4

Источник

ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-14

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

РубрикиРубрики
Задачи по номерам!

№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
МЕТКИ

БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Задание 12. Найдите наименьшее значение функции у = 5cosx +6х + 6 на отрезке .

Решение.

1. Для нахождения наименьшего значения функции на интервале, найдем сначала точки экстремума функции, принадлежащие этому интервалу. Для этого вычислим производную функции и приравняем ее нулю, имеем:

то есть точки экстремума отсутствуют.

2. Вычислим значения функции на границах интервала, получим:

Второе значение явно больше 11, следовательно, наименьшее значение функции равно 11.

Ответ: 11.

Задание 12. Найдите точку максимума функции .

Решение.

Вычислим производную от функции, получим

Приравняем производную нулю и найдем точки экстремума функции

В точке максимума знак производной меняется с положительного на отрицательный. Анализ двух точек экстремума показывает, что точка максимума соответствует точке -27.

Ответ: -27.

Задание 12. Найдите наибольшее значение функции на отрезке .

Решение.

Вычислим производную от функции y, получим:

В точках экстремума производная равна нулю, т.е.

следовательно, максимальное и минимальное значение функции находятся на границах диапазона . Вычислим значение функции в этих точках, получим:

данное значение не может быть выражено конечной десятичной дробью, а значит не является ответом в ЕГЭ;

точка максимума функции на отрезке.

Ответ: 11.

Задание 12. Найдите точку максимума функции .

Решение.

Преобразуем выражение, получим:

Вычислим производную, имеем:

В точках экстремума функции производная равна нулю, получаем уравнение

Решаем квадратное уравнение, получаем два корня:

В точке максимума производная должна из положительной области переходить в отрицательную. Анализируя полученные точки, видим, что при , производная меняет свой знак с «+» на «-», а в точке с «-» на «+», следовательно, точка является точкой максимума.

Ответ: 3.

Задание 12. Найдите точку максимума функции .

Решение.

Преобразуем выражение, получим:

Вычислим производную, имеем:

В точках экстремума функции производная равна нулю, получаем уравнение

Решаем квадратное уравнение, получаем два корня:

Ответ: 3.

Задание 12. Найдите наименьшее значение функции на отрезке [9; 36].

Решение.

Преобразуем выражение

Производная равна

В точках экстремума функции производная равна нулю, получаем уравнение

Рассмотрим значения функции в граничных точках диапазона, получим:

Наименьшее значение равно -77.

Ответ: -77.

Задание 12. Найдите наибольшее значение функции на отрезке [-3; 1].

Решение.

Вычислим производную от функции, получим

В точках экстремума функции производная равна нулю, имеем:

Решение уравнения дает два корня

— не принадлежит множеству действительных чисел

Значение и остается одна точка . Вычислим значения функции в точке экстремума -2 и в граничных точках -3 и 1, получим:

Наибольшее значение функции равно 48.

Ответ: 48.

Задание 12. Найдите наименьшее значение функции на отрезке [20; 22].

Решение.

Вычислим производную

В точках экстремума производная равна нулю, получим уравнение

Для определения наименьшего значения функции, вычислим ее значение на краях диапазона и в точке экстремума, получим:

данное значение не может быть выражено конечной десятичной дробью, а значит не является ответом в ЕГЭ;

Наименьшее значение равно -1.

Ответ: -1.

Узнай свой уровень знаний по математике всего за 8 минут. Все, что нужно, — это честность!

Знакомься. Наш супер-тест для тех, кто перешел в 11-й класс: Анкета

А также для родителей, который собираются самостоятельно подготовить «ребенка» к ЕГЭ.

И даже для учителей.

Всего 8 минут и никакого решения задач.

Ты просто отвечаешь: «Да» или «Нет» Анкета

Читай вопросы внимательно.

Обрати внимание, что здесь нет вариантов «получается иногда» или «однажды видел, как это делать». Если решаешь «пятьдесят на пятьдесят», лучше честно указать: «не решаю». Зачем обманывать себя?

Заодно узнаешь, какие вообще темы есть на ЕГЭ по математике в каждой из 19 задач Профильного уровня.

В конце нажми кнопку «Посчитать».

Как ты догадался, результат – твои тестовые баллы на ЕГЭ.

Тест разработан Анной Малковой и командой ЕГЭ-Студии. Проверен и откалиброван. Его проходили десятки наших учеников, и результаты с высокой точностью совпадали с теми, которые они получали на Пробных ЕГЭ.

Мы также подготовили для тебя варианты Профильного ЕГЭ по математике с решениями и ответами.

ЕГЭ, профильный уровень. Тренировочный вариант 1
ЕГЭ, профильный уровень. Тренировочный вариант 2
ЕГЭ, профильный уровень. Тренировочный вариант 3
ЕГЭ, профильный уровень. Тренировочный вариант 4
ЕГЭ, профильный уровень. Тренировочный вариант 5
ЕГЭ-2018, профильный уровень. Разбор задач 13-19
Нерешаемые задачи ЕГЭ по математике
Стрим 20 августа 2020 года. Лучшие задачи ЕГЭ-2020

Рекомендации по решению вариантов:

1. Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по одной и старайтесь довести до ответа.

2. Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Например, на нашем Онлайн-курс подготовки к ЕГЭ

3. Как оценить свой уровень?

Вам поможет наша Таблица перевода первичных баллов ЕГЭ в тестовые

Задания 1 части (№1 – 12) оцениваются в 1 первичный балл каждое.

Задания 13, 14, 15 – в 2 первичных балла каждое,

Задания 16 и 17 – 3 балла,

Задания 18 и 19 – 4 балла!

Если вы набрали не менее 60 тестовых баллов за весь вариант – у вас высокие шансы сдать ЕГЭ на 90+. Если заниматься, конечно.

Если набрали около 40 баллов… что же, это типичная картина на старте 11-го класса. И даже для того, чтобы получить 70+, надо будет хорошо поработать. И тем более для 80+ и 90+. И не расстраивайтесь – у наших учеников это хорошо получается.

Если ниже 35 баллов – значит, увы, уже отстаете.

Потому что многие задания ЕГЭ – например, задачи 1, 2, 3, 4, 6, 8, 11 и даже 16… — легко может решить и учащийся 9-10 класса.

4. Обязательно разберите правильные решения. Удачи!

Решу ЕГЭ математика 2022 год: профильный уровень, база Дмитрия Гущина, демоверсия ФИПИ. Получить ответы и решения за 11 класс можно внизу страницы бесплатно через онлайн-форму.

Главная » Решу ЕГЭ математика 2022 год

Хотите, решу ЕГЭ по математике профиль 2022

Ищете, где решить ЕГЭ по профильной математике Дмитрия Гущина за 2022 год? На нашем сайте демоврсия по предмету ФИПИ, база знаний. Все ответы по профилю математика и другим предметам можете получить через бесплатную онлайн-форму внизу страницы.

Решу ЕГЭ математика 11 класс 2022 профиль

Детские сады по районам города
Официальные сайты
Режим работы
Расположение на карте

Численность населения города
Сколько человек проживает
Районы и улицы
Расположение на карте

Список районов
Официальный сайт администрации
Адреса по улицам
Расположение на карте

Школы по районам города
Официальные сайты образовательных учреждений
Рейтинг лучших
Расположение на карте

Как получить доступ к решу ЕГЭ по математике 2022 за 11 класс

Зайти на сайт

Зарегистрироваться внизу страницы

Уточнить информацию

Воспользоваться строкой поиска

Указать пожелания

Чтобы получать бесплатную информацию, билеты, акции, скидки

Отправить запрос

В подвале сайта заполнить быструю онлайн-форму

Что включает в себя решу ЕГЭ 2022 математика

Профильный предмет по базе Дмитрия Гущина;
Варианты ответов;
Доступ к сайту решу ЕГЭ.

Реши и распечатай ЕГЭ по математике за 2022 год

Решу ЕГЭ математика 2022 год профиль и дам доступ в демоверсию с ответами. Подробнее через бесплатную онлайн-форму заявки.

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.admin2023-03-05T19:16:30+03:00

Источник

9 марта 2023

В закладки

Обсудить

Жалоба

Теория и практика.

Содержание

1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой
Тригонометрические функции
9) Показательные функции
10) Логарифмические функции

10_zadacha.pdf

Источник: vk.com/profimatika

Источник

Добавить комментарий

Хотите, решу ЕГЭ по математике профиль 2022

Решу ЕГЭ математика 11 класс 2022 профиль

Как получить доступ к решу ЕГЭ по математике 2022 за 11 класс

Что включает в себя решу ЕГЭ 2022 математика

Реши и распечатай ЕГЭ по математике за 2022 год

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.

Новое и интересное на сайте: