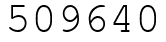Решу егэ математика 509640 - Помощь в подготовке к экзаменам и поступлению

Задания

Версия для печати и копирования в MS Word

Тип 12 № 509640

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 11. Найдите площадь заштрихованной фигуры.

Спрятать решение

Решение.

Площади кругов относятся как квадраты их радиусов. Поскольку радиус большего круга вдвое больше радиуса меньшего круга, площадь большего круга вчетверо больше площади меньшего. Следовательно, она равна 44. Площадь заштрихованной фигуры равна разности площадей кругов: 44 − 11  =  33.

Ответ: 33.

Аналоги к заданию № 315122: 509640 315235 315237 315239 315241 315243 315245 315247 315249 315251 … Все

Спрятать решение

Прототип задания

Сообщить об ошибке · Помощь

Источник

509638
1, 2, 37, 71, 74, 97, 142, 194, 2627, 3589, 5254, 6887, 7178, 13774, 254819, 509638

509639
1, 13, 197, 199, 2561, 2587, 39203, 509639

509640
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 31, 40, 60, 62, 93, 120, 124, 137, 155, 186, 248, 274, 310, 372, 411, 465, 548, 620, 685, 744, 822, 930, 1096, 1240, 1370, 1644, 1860, 2055, 2740, 3288, 3720, 4110, 4247, 5480, 8220, 8494, 12741, 16440, 16988, 21235, 25482, 33976, 42470, 50964, 63705, 84940, 101928, 127410, 169880, 254820, 509640

509641
1, 11, 107, 433, 1177, 4763, 46331, 509641

509642
1, 2, 7, 14, 59, 118, 413, 617, 826, 1234, 4319, 8638, 36403, 72806, 254821, 509642

509643
1, 3, 9, 17, 51, 153, 3331, 9993, 29979, 56627, 169881, 509643

509644
1, 2, 4, 103, 206, 412, 1237, 2474, 4948, 127411, 254822, 509644

509645
1, 5, 101929, 509645

509646
1, 2, 3, 6, 29, 58, 87, 101, 174, 202, 303, 606, 841, 1682, 2523, 2929, 5046, 5858, 8787, 17574, 84941, 169882, 254823, 509646

509647
1, 509647

509648
1, 2, 4, 8, 16, 53, 106, 212, 424, 601, 848, 1202, 2404, 4808, 9616, 31853, 63706, 127412, 254824, 509648

509649
1, 3, 7, 21, 49, 147, 3467, 10401, 24269, 72807, 169883, 509649

509650
1, 2, 5, 10, 25, 50, 10193, 20386, 50965, 101930, 254825, 509650

509651
1, 127, 4013, 509651

509652
1, 2, 3, 4, 6, 9, 11, 12, 13, 18, 22, 26, 27, 33, 36, 39, 44, 52, 54, 66, 78, 81, 99, 108, 117, 121, 132, 143, 156, 162, 198, 234, 242, 286, 297, 324, 351, 363, 396, 429, 468, 484, 572, 594, 702, 726, 858, 891, 1053, 1089, 1188, 1287, 1404, 1452, 1573, 1716, 1782, 2106, 2178, 2574, 3146, 3267, 3564, 3861, 4212, 4356, 4719, 5148, 6292, 6534, 7722, 9438, 9801, 11583, 13068, 14157, 15444, 18876, 19602, 23166, 28314, 39204, 42471, 46332, 56628, 84942, 127413, 169884, 254826, 509652

509653
1, 509653

509654
1, 2, 254827, 509654

509655
1, 3, 5, 15, 61, 183, 305, 557, 915, 1671, 2785, 8355, 33977, 101931, 169885, 509655

509656
1, 2, 4, 7, 8, 14, 19, 28, 38, 56, 76, 133, 152, 266, 479, 532, 958, 1064, 1916, 3353, 3832, 6706, 9101, 13412, 18202, 26824, 36404, 63707, 72808, 127414, 254828, 509656

509657
1, 23, 22159, 509657

509658
1, 2, 3, 6, 173, 346, 491, 519, 982, 1038, 1473, 2946, 84943, 169886, 254829, 509658

509659
1, 509659

509660
1, 2, 4, 5, 10, 17, 20, 34, 68, 85, 170, 340, 1499, 2998, 5996, 7495, 14990, 25483, 29980, 50966, 101932, 127415, 254830, 509660

509661
1, 3, 9, 56629, 169887, 509661

509662
1, 2, 254831, 509662

509663
1, 7, 11, 77, 6619, 46333, 72809, 509663

509664
1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96, 5309, 10618, 15927, 21236, 31854, 42472, 63708, 84944, 127416, 169888, 254832, 509664

509665
1, 5, 13, 65, 7841, 39205, 101933, 509665

509666
1, 2, 254833, 509666

509667
1, 3, 169889, 509667

Источник

Рациональное неотрицательное
шестизначное

число 509640
– составное.

24 — сумма цифр данного числа.
64 — количество делителей числа 509640.
Сумма делителей этого числа: 1589760.
509640 и 0.0000019621693744604036 являются обратными числами.

Это число представляется произведением простых чисел: 2 * 2 * 2 * 3 * 5 * 31 * 137.

Другие системы счисления:
двоичный вид числа: 1111100011011001000, троичный вид числа: 221220002120, восьмеричный вид числа: 1743310, шестнадцатеричный вид числа: 7C6C8.
Перевод из числа байтов — 497 килобайтов 712 байтов .

В виде кода азбуки Морзе: ….. —— —-. -…. ….- ——

Число — не число Фибоначчи.

Косинус 509640: -0.1552, синус 509640: -0.9879, тангенс 509640: 6.3648.
У числа есть натуральный логарифм: 13.1415.
Логарифм десятичный равен 5.7073.
713.8907 — корень квадратный из числа 509640, 79.8769 — корень кубический.
Возведение числа в квадрат: 2.5973e+11.

Число секунд 509640 это 5 дней 21 час 34 минуты ноль секунд.
Нумерологическая цифра этого числа — 6.

Источник

Свойства натурального числа 509640, 0x07C6C8, 0x7C6C8:

Рейтинг 0 из 10,
оценок: 0.

Системы счисления, перевод в систему счисления

Десятичное число 509640

509640 в шестнадцатеричной системе счисления

7C6C8
509640 в двоичной системе счисления

1111100011011001000
509640 в восьмеричной системе счисления

1743310

Шестнадцатеричное число 7C6C8

7C6C8 в десятичной системе

509640
7C6C8 в двоичной системе

1111100011011001000
7C6C8 в восьмеричной системе

1743310

Двоичное число 1111100011011001000

1111100011011001000 в десятичной системе

509640
1111100011011001000 в шестнадцатеричной системе

7C6C8
1111100011011001000 в восьмеричной системе

1743310

Восьмеричное число 1743310

1743310 в десятичной системе

509640
1743310 в шестнадцатеричной системе

7C6C8
1743310 в двоичной системе

1111100011011001000

Основные арифметические и алгебраические свойства

Число 509640 на русском языке, number in Russian, число 509640 прописью:

пятьсот девять тысяч шестьсот сорок
Четность

Четное число 509640
Разложение на множители, делители числа 509640

2, 2, 2, 3, 5, 31, 137, 1
Простое или составное число

Составное число 509640
Числа делящиеся на целое число 509640

1019280, 1528920, 2038560, 2548200, 3057840, 3567480, 4077120, 4586760
Число 509640 умноженное на число два

1019280
509640 деленное на число 2

254820
Список 8-ми простых чисел перед числом

509633, 509623, 509603, 509591, 509581, 509573, 509569, 509563
Сумма десятичных цифр

24
Количество цифр

6
Десятичный логарифм 509640

5.7072635070383
Натуральный логарифм 509640

13.141459873095
Это число Фибоначчи?

Нет
Число на 1 больше числа 509640,
следующее число

число 509641
Число на 1 меньше числа 509640,
предыдущее число

509639

Степени числа, корни

509640 во второй степени (в квадрате)
(функция x в степени 2 — x²)

259732929600
В третьей степени (в кубе, 509640 в степени 3, x³) равно

132370290241344000
Корень квадратный из 509640

713.89074794397
Корень кубический из числа 509640 =

79.876893991889

Тригонометрические функции, тригонометрия

Синус, sin 509640 градусов, sin 509640°

-0.8660254038
Косинус, cos 509640 градусов, cos 509640°

-0.5
Тангенс, tg 509640 градусов, tg 509640°

1.7320508076
Синус, sin 509640 радиан

-0.98788156132193
Косинус, cos 509640 радиан

-0.1552096027962
Тангенс, tg 509640 радиан равно

6.3648224306009
509640 градусов, 509640° =

8894.8959998639 радиан
509640 радиан =

29200221.071047 градуса, 29200221.071047°

Контрольные суммы, хэши, криптография

MD-5 хэш(509640)

a17e6ed1884d14c67b6185634097f577
CRC-32, CRC32(509640)

1952604777
SHA-256 hash, SHA256(509640)

2a6fbe13c2b37ba445cce7f496a422f7ea9d1544ea8a87584e408996f3010985
SHA1, SHA-1(509640)

96c950c1780ebed2ed6a5359af4aec42ce785d1d
ГОСТ Р 34.11, GOST R 34.11-94, GOST(509640)

eeec9f2f28fe85263b52b4f023997df3d737914fd5e55bb7724b5de43dc36e45
Base64

NTA5NjQw

Языки программирования

C++, CPP, C значение 509640

0x07C6C8, 0x7C6C8
Delphi, Pascal значение числа 509640

$07C6C8

Дата и время

Конвертация UNIX timestamp 509640 в дату и время

UTC

вторник, 6 января 1970 г., 21:34:00 GMT

в Москве, Россия

среда, 7 января 1970 г., 0:34:00 Московское стандартное время

в Лондоне, Великобритания

вторник, 6 января 1970 г., 22:34:00 GMT+01:00

в Нью-Йорке, США

вторник, 6 января 1970 г., 16:34:00 Восточно-американское стандартное время

Интернет

Конвертация в IPv4 адрес Интернет

0.7.198.200
509640 в Википедии:

509640

Другие свойства числа

Короткая ссылка на эту страницу, DEC

https://bikubik.com/ru/509640
Короткая ссылка на эту страницу, HEX

https://bikubik.com/ru/x7C6C8
Номер телефона

50-96-40

Цвет по числу 509640, цветовая гамма

html RGB цвет 509640, 16-ричное значение

#07C6C8 — (7, 198, 200)
HTML CSS код цвета #07C6C8

.color-mn { color: #07C6C8; }
.color-bg { background-color: #07C6C8; }

Цвет для данного числа 509640

Здесь вы можете изменить составляющую цвета для данного числа 509640 или цвета 07C6C8:

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Системы счисления, перевод в систему счисления

Десятичное число 509640

Шестнадцатеричное число 7C6C8

Двоичное число 1111100011011001000

Восьмеричное число 1743310

Основные арифметические и алгебраические свойства

Степени числа, корни

Тригонометрические функции, тригонометрия

Контрольные суммы, хэши, криптография

Языки программирования

Дата и время

Интернет

Другие свойства числа

Цвет по числу 509640, цветовая гамма

Новое и интересное на сайте: