При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Найдите значение выражения
Ответ:
2
Найдите значение выражения
Ответ:
3
Железнодорожный билет для взрослого стоит 720 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 15 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу?
Ответ:
4
Площадь трапеции S в м2 можно вычислить по формуле где
— основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 5, b = 3 и h = 6.
Ответ:
5
Найдите значение выражения если
Ответ:
6
Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пакетиков нужно купить хозяйке для приготовления 6 литров маринада?
Ответ:
7
Найдите корень уравнения:
Ответ:
8
9
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) расстояние от дома до школы
Б) расстояние от Земли до Марса
В) расстояние от Амстердама до Парижа
Г) расстояние между глазами человека
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 65 мм
2) 1 км
3) 500 км
4) 55 · 106 км
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
10
В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 9 спортсменов из Сербии, 8 спортсменов из Хорватии и 10 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Сербии.
Ответ:
11
На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 30 марта 1959 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линиями. Определите по рисунку, какой была наибольшая среднесуточная температура за указанный период. Ответ дайте в градусах Цельсия.
Ответ:
12
13
Первый и второй насосы наполняют бассейн за 10 минут, второй и третий — за 15 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Ответ:
14
Найдите наименьшее значение функции на отрезке
Ответ:
15
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 38 и 23. Найдите среднюю линию этой трапеции.
Ответ:
16
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Ответ:
17
На прямой отмечены точки A, B, C и D.
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
18
Известно, что все щуки — рыбы, также известно, что все рыбы плавают в воде. Тюлень тоже плавает в воде. Выберите утверждения, которые следуют из приведённых данных.
1) Все тюлени — рыбы
2) Если животное не плавает, то это не тюлень
3) Все щуки плавают в воде
4) Если животное плавает в воде, то оно либо рыба, либо тюлень
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ:
19
Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.
Ответ:
20
Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
509638
1, 2, 37, 71, 74, 97, 142, 194, 2627, 3589, 5254, 6887, 7178, 13774, 254819, 509638
509639
1, 13, 197, 199, 2561, 2587, 39203, 509639
509640
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 31, 40, 60, 62, 93, 120, 124, 137, 155, 186, 248, 274, 310, 372, 411, 465, 548, 620, 685, 744, 822, 930, 1096, 1240, 1370, 1644, 1860, 2055, 2740, 3288, 3720, 4110, 4247, 5480, 8220, 8494, 12741, 16440, 16988, 21235, 25482, 33976, 42470, 50964, 63705, 84940, 101928, 127410, 169880, 254820, 509640
509641
1, 11, 107, 433, 1177, 4763, 46331, 509641
509642
1, 2, 7, 14, 59, 118, 413, 617, 826, 1234, 4319, 8638, 36403, 72806, 254821, 509642
509643
1, 3, 9, 17, 51, 153, 3331, 9993, 29979, 56627, 169881, 509643
509644
1, 2, 4, 103, 206, 412, 1237, 2474, 4948, 127411, 254822, 509644
509645
1, 5, 101929, 509645
509646
1, 2, 3, 6, 29, 58, 87, 101, 174, 202, 303, 606, 841, 1682, 2523, 2929, 5046, 5858, 8787, 17574, 84941, 169882, 254823, 509646
509647
1, 509647
509648
1, 2, 4, 8, 16, 53, 106, 212, 424, 601, 848, 1202, 2404, 4808, 9616, 31853, 63706, 127412, 254824, 509648
509649
1, 3, 7, 21, 49, 147, 3467, 10401, 24269, 72807, 169883, 509649
509650
1, 2, 5, 10, 25, 50, 10193, 20386, 50965, 101930, 254825, 509650
509651
1, 127, 4013, 509651
509652
1, 2, 3, 4, 6, 9, 11, 12, 13, 18, 22, 26, 27, 33, 36, 39, 44, 52, 54, 66, 78, 81, 99, 108, 117, 121, 132, 143, 156, 162, 198, 234, 242, 286, 297, 324, 351, 363, 396, 429, 468, 484, 572, 594, 702, 726, 858, 891, 1053, 1089, 1188, 1287, 1404, 1452, 1573, 1716, 1782, 2106, 2178, 2574, 3146, 3267, 3564, 3861, 4212, 4356, 4719, 5148, 6292, 6534, 7722, 9438, 9801, 11583, 13068, 14157, 15444, 18876, 19602, 23166, 28314, 39204, 42471, 46332, 56628, 84942, 127413, 169884, 254826, 509652
509653
1, 509653
509654
1, 2, 254827, 509654
509655
1, 3, 5, 15, 61, 183, 305, 557, 915, 1671, 2785, 8355, 33977, 101931, 169885, 509655
509656
1, 2, 4, 7, 8, 14, 19, 28, 38, 56, 76, 133, 152, 266, 479, 532, 958, 1064, 1916, 3353, 3832, 6706, 9101, 13412, 18202, 26824, 36404, 63707, 72808, 127414, 254828, 509656
509657
1, 23, 22159, 509657
509658
1, 2, 3, 6, 173, 346, 491, 519, 982, 1038, 1473, 2946, 84943, 169886, 254829, 509658
509659
1, 509659
509660
1, 2, 4, 5, 10, 17, 20, 34, 68, 85, 170, 340, 1499, 2998, 5996, 7495, 14990, 25483, 29980, 50966, 101932, 127415, 254830, 509660
509661
1, 3, 9, 56629, 169887, 509661
509662
1, 2, 254831, 509662
509663
1, 7, 11, 77, 6619, 46333, 72809, 509663
509664
1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96, 5309, 10618, 15927, 21236, 31854, 42472, 63708, 84944, 127416, 169888, 254832, 509664
509665
1, 5, 13, 65, 7841, 39205, 101933, 509665
509666
1, 2, 254833, 509666
509667
1, 3, 169889, 509667
На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 509646?
На число 509646 без остатка (нацело) делятся следующие числа: 509646, 1019292, 1528938, 2038584, 2548230, 3057876, 3567522, 4077168, 4586814, 5096460, 5606106, 6115752 и многие другие.
Какие четные числа делятся на 509646?
На число 509646 делятся следующие четные числа: 509646, 1019292, 1528938, 2038584, 2548230, 3057876, 3567522, 4077168, 4586814, 5096460, 5606106, 6115752 и многие други.
Какие нечетные числа делятся на 509646?
Таких чисел нет
На какое наибольшее число делится число 509646 без остатка?
Наибольшее число на которое делится число 509646 есть само число 509646. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 509646 без остатка, не считая числа 509646 и 1?
Наибольшим делителем числа 509646 не считая самого числа 509646 является число 254823.
Какое наименьшее натуральное число делится на 509646?
Наименьшее натуральное число которое делиться на число 509646 является само число 509646.
На какое наименьшее натуральное число делится число 509646?
Наименьшее натуральное число на которое можно разделить число 509646 — это число 1.
Делители числа 509646.
(что бы не забыть запишите все делители числа 509646 в блокнот.)На какие целые и(или) натуральные числа делится число 509646?
Число 509646 делится на следующие целые, натуральные числа (все делители числа 509646): 1, 2, 3, 6, 29, 58, 87, 101, 174, 202, 303, 606, 841, 1682, 2523, 2929, 5046, 5858, 8787, 17574, 84941, 169882, 254823, 509646
На какие четные числа делится число 509646?
Число 509646 делится на следующие четные числа (четные делители числа): 2, 6, 58, 174, 202, 606, 1682, 5046, 5858, 17574, 169882, 509646
На какие нечетные числа делится число 509646?
Число 509646 делится на следующие нечетные числа (нечетные делители числа): 1, 3, 29, 87, 101, 303, 841, 2523, 2929, 8787, 84941, 254823
Сколько делителей имеет число 509646?
Число 509646 имеет 24 делителя
Сколько четных делителей имеет число 509646?
Число 509646 имеет 12 четных делителей
Сколько нечетных делителей имеет число 509646?
Число 509646 имеет 12 нечетных делителей
Число 509646 прописью, словами.
— пятьсот девять тысяч шестьсот сорок шесть
(что бы не забыть запишите число 509646 прописью в блокнот.)
Числа кратные 509646.
— кратные числа, числу 509646 : 1019292, 1528938, 2038584, 2548230, 3057876, 3567522, 4077168, 4586814, 5096460, 5606106, 6115752 и многие другие.
Простые множители числа 509646.
У числа 509646 нет простых множителей кроме 1.
Сумма цифр числа 509646.
Сумма цифр числа 509646 равна 30
Произведение цифр числа 509646.
Произведение цифр числа 509646 равна 0
Квадрат числа 509646.
Квадрат числа 509646 равен 259739045316
Куб числа 509646.
Куб числа 509646 равен 132374965489118136
Квадратный корень числа 509646.
Квадратный корень числа 509646 равен 713.8949.
Число 509646 в двоичной системе счисления.
Запись числа 509646 в двоичной системе счисления выглядит так: 1111100011011001110
Количество значащих нулей в двоичной записи числа 509646 = 7
Количество едениц в двоичной записи числа 509646 = 12
(что бы не забыть запишите число 509646 в двоичной системе счисления в блокнот.)Число 509646 в шестнадцатеричной системе счисления.
Запись числа 509646 в шестнадцатеричной системе счисления выглядит так: 7c6ce
(что бы не забыть запишите число 509646 в шестнадцатеричной системе счисления в блокнот.)Число 509646 в восьмеричной системе счисления.
Запись числа 509646 в восьмеричной системе счисления выглядит так: 1743316
(что бы не забыть запишите число 509646 в восьмеричной системе счисления в блокнот.)Число 509646 не является простым!
Корни числа 509646.
Корень 3 степени из 509646.
Корень 3 (третьей) степени из 509646 равен 79.877207454649
Корень 4 степени из 509646.
Корень 4 (четвертой) степени из 509646 равен 26.718812665523
Корень 5 степени из 509646.
Корень 5 (пятой) степени из 509646 равен 13.850125988138
Корень 6 степени из 509646.
Корень 6 (шестой) степени из 509646 равен 8.9374049619925
Корень 7 степени из 509646.
Корень 7 (седьмой) степени из 509646 равен 6.5361812767356
Корень 8 степени из 509646.
Корень 8 (восьмой) степени из 509646 равен 5.1690243436767
Корень 9 степени из 509646.
Корень 9 (девятой) степени из 509646 равен 4.3066636801691
Корень 10 степени из 509646.
Корень 10 (десятой) степени из 509646 равен 3.7215757399438
Корень 11 степени из 509646.
Корень 11 (одиннадцатой) степени из 509646 равен 3.3024982930536
Корень 12 степени из 509646.
Корень 12 (двенадцатой) степени из 509646 равен 2.9895492907782
Корень 13 степени из 509646.
Корень 13 (тринадцатой) степени из 509646 равен 2.7480248968577
Корень 14 степени из 509646.
Корень 14 (четырнадцатой) степени из 509646 равен 2.5565956420082
Корень 15 степени из 509646.
Корень 15 (пятнадцатой) степени из 509646 равен 2.4015109691487
Степени числа 509646.
509646 в 3 степени.
509646 в 3 степени равно 132374965489118136.
509646 в 4 степени.
509646 в 4 степени равно 6.7464371661667E+22.
509646 в 5 степени.
509646 в 5 степени равно 3.4382947159882E+28.
509646 в 6 степени.
509646 в 6 степени равно 1.7523131488245E+34.
509646 в 7 степени.
509646 в 7 степени равно 8.9305938704582E+39.
509646 в 8 степени.
509646 в 8 степени равно 4.5514414437036E+45.
509646 в 9 степени.
509646 в 9 степени равно 2.3196239260177E+51.
509646 в 10 степени.
509646 в 10 степени равно 1.1821870553992E+57.
509646 в 11 степени.
509646 в 11 степени равно 6.02496904036E+62.
509646 в 12 степени.
509646 в 12 степени равно 3.0706013715433E+68.
509646 в 13 степени.
509646 в 13 степени равно 1.5649197066016E+74.
509646 в 14 степени.
509646 в 14 степени равно 7.9755506879066E+79.
509646 в 15 степени.
509646 в 15 степени равно 4.0647075058888E+85.
Какое число имеет такую же сумму цифр как и число 509646?Математика. Найти сумму цифр числа 509646.
Число 509646 состоит из следующих цифр — 5, 0, 9, 6, 4, 6.
Определить сумму цифр числа 509646 не так уж и сложно.
Сумма цифр шестизначного числа 509646 равна 5 + 0 + 9 + 6 + 4 + 6 = 30.
Числа сумма цифр которых равна 30.
Следующие числа имеют такую же сумму цифр как и число 509646 — 3999, 4899, 4989, 4998, 5799, 5889, 5898, 5979, 5988, 5997, 6699, 6789, 6798, 6879, 6888, 6897, 6969, 6978, 6987, 6996.
Четырехзначные числа сумма цифр которых равна 30 — 3999, 4899, 4989, 4998, 5799, 5889, 5898, 5979, 5988, 5997.
Пятизначные числа сумма цифр которых равна 30 — 12999, 13899, 13989, 13998, 14799, 14889, 14898, 14979, 14988, 14997.
Шестизначные числа сумма цифр которых равна 30 — 102999, 103899, 103989, 103998, 104799, 104889, 104898, 104979, 104988, 104997.
Квадрат суммы цифр числа 509646.
Квадрат суммы цифр шестизначного числа 509646 равен 5 + 0 + 9 + 6 + 4 + 6 = 30² = 900.
Сумма квадратов цифр шестизначного числа 509646.
Сумма квадратов цифр числа 509646 равна 5² + 0² + 9² + 6² + 4² + 6² = 25 + 0 + 81 + 36 + 16 + 36 = 194.
Сумма четных цифр числа 509646.
Сумма четных цифр шестизначного числа 509646 равна 6 + 4 + 6 = 16.
Квадрат суммы четных цифр шестизначного числа 509646.
Квадрат суммы четных цифр числа 509646 равна 6 + 4 + 6 = 16² = 256.
Сумма квадратов четных цифр шестизначного числа 509646.
Сумма квадратов четных цифр числа 509646 равна 6² + 4² + 6² = 36 + 16 + 36 = 88.
Сумма нечетных цифр числа 509646.
Сумма нечетных цифр шестизначного числа 509646 равна 5 + 9 = 14.
Квадрат суммы нечетных цифр шестизначного числа 509646.
Квадрат суммы нечетных цифр числа 509646 равна 5 + 9 = 14² = 196.
Сумма квадратов нечетных цифр шестизначного числа 509646.
Сумма квадратов нечетных цифр числа 509646 равна 5² + 9² = 25 + 81 = 106.
Произведение цифр числа 509646.
Какое число имеет такое же произведение цифр как и число 509646?Математика. Найти произведение цифр числа 509646.
Число 509646 состоит из следующих цифр — 5, 0, 9, 6, 4, 6.
Найти сумму цифр числа 509646 просто.
Решение:
Произведение цифр числа 509646 равно 5 * 0 * 9 * 6 * 4 * 6 = 0.
Числа произведение цифр которых равно 0.
Следующие числа имеют такое же произведение цифр как и число 509646 — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.
Двухзначные числа произведение цифр которых равно 0 — 10, 20, 30, 40, 50, 60, 70, 80, 90.
Трехзначные числа произведение цифр которых равно 0 — 100, 101, 102, 103, 104, 105, 106, 107, 108, 109.
Четырехзначные числа произведение цифр которых равно 0 — 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009.
Пятизначные числа произведение цифр которых равно 0 — 10000, 10001, 10002, 10003, 10004, 10005, 10006, 10007, 10008, 10009.
Шестизначные числа произведение цифр которых равно 0 — 100000, 100001, 100002, 100003, 100004, 100005, 100006, 100007, 100008, 100009.
Квадрат произведения цифр числа 509646.
Квадрат произведения цифр шестизначного числа 509646 равен 5 * 0 * 9 * 6 * 4 * 6 = 0² = 0.
Произведение квадратов цифр шестизначного числа 509646.
Произведение квадратов цифр числа 509646 равна 5² * 0² * 9² * 6² * 4² * 6² = 25 * 0 * 81 * 36 * 16 * 36 = 0.
Произведение четных цифр числа 509646.
Произведение четных цифр шестизначного числа 509646 равно 6 * 4 * 6 = 144.
Квадрат произведения четных цифр шестизначного числа 509646.
Квадрат произведения четных цифр числа 509646 равен 6 * 4 * 6 = 144² = 20736.
Произведение квадратов четных цифр шестизначного числа 509646.
Произведение квадратов четных цифр числа 509646 равно 6² * 4² * 6² = 36 * 16 * 36 = 20736.
Запишите числа которые в сумме дают число 509646.
Задача: Данно число 509646.Какие 2(два) числа дают в сумме число 509646?Решение:
1) 82949 + 426697 = 509646
2) 77218 + 432428 = 509646
3) 232755 + 276891 = 509646
4) 238425 + 271221 = 509646
5) 226266 + 283380 = 509646
Какие 3(три) числа дают в сумме число 509646?Решение:
1) 146758 + 53924 + 308964 = 509646
2) 122630 + 151555 + 235461 = 509646
3) 81264 + 110826 + 317556 = 509646
4) 86027 + 168791 + 254828 = 509646
5) 53399 + 97061 + 359186 = 509646
Какие 4(четыре) числа дают в сумме число 509646?Решение:
1) 72995 + 5952 + 35483 + 395216 = 509646
2) 124484 + 53723 + 65404 + 266035 = 509646
3) 97394 + 44810 + 75471 + 291971 = 509646
4) 39145 + 23832 + 207568 + 239101 = 509646
5) 46750 + 61535 + 73576 + 327785 = 509646
Какие 5(пять) чисел дают в сумме число 509646?Решение:
1) 89024 + 26004 + 136728 + 111699 + 146191 = 509646
2) 85521 + 99131 + 29226 + 43006 + 252762 = 509646
3) 43756 + 69463 + 4994 + 44382 + 347051 = 509646
4) 52866 + 48149 + 41351 + 4883 + 362397 = 509646
5) 46137 + 39698 + 82926 + 3695 + 337190 = 509646
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х^2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
$ax^2 + c = 0$
$ax^2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.
$x^2 — 16 = 0$
$x^2 = 16$
$x = ±4$
Ответ: $х_1 = 4, х_2 = — 4$
Решение полного квадратного уравнения
Решение с помощью дискриминанта
Дискриминантом квадратного уравнения D называется выражение
$b^2 — 4ac$.
При решении уравнения с помощью дискриминанта возможны три случая:
1. $D > 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х^2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней
$3х^2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х^2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х^2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)^3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)^3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4x^2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х^2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
Например,
${2}/{x}+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-{3}/{x}=0$
Решение:
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x ≠ 0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x+1-{3}/{x}=0|·x$
$4x·x+1·x-{3·x}/{x}=0$
3. решаем полученное уравнение
$4x^2+x-3=0$
Решим вторым устным способом, т.к. $а+с=b$
Тогда, $x_1=-1, x_2=-{3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=-1, x_2=-{3}/{4}$
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$
Решить уравнение ${3x-5}/{-2}={1}/{x}$
Решение:
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х(3х-5)=-2$
Раскроем скобки и соберем все слагаемые в левой стороне
$3х^2-5х+2=0$
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
$x_1=1, x_2={2}/{3}$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=1, x_2={2}/{3}$
Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.
Чтобы решить иррациональное уравнение, необходимо:
- Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
- Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
- Решить полученное рациональное уравнение.
- Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.
Решение:
Обе части уравнение возведем в квадрат:
$√{4х-3}^2=х^2$
Получаем квадратное уравнение:
$4х-3=х^2$
Перенесем все слагаемые в левую часть уравнения:
${-х}^2+4х-3=0$
Решим данное квадратное уравнение устным способом, так как
$a+b+c=0$
$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$√{4·1-3}=1$
$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.
$√{4·(3)-3}=3$
$√9=3$
$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит
$х_1=1$ наименьший корень.
Ответ: $1$
Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$
Решить уравнение: $х-6=√{8-х}$
Возведем обе части уравнения в квадрат
$(х-6)^2=8-х$
В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение
$х^2-2·6·х+6^2=8-х$
$х^2-12х+36=8-х$
Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.
$х^2-12х+36-8+х=0$
Приводим подобные слагаемые:
$х^2-11х+28=0$
Найдем корни уравнения через дискриминант:
$D=b^2-4ac=121-4·28=121-112=9=3^2$
$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$
$x_1=7; x_2=4$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$x_1=7$
$7-6=√{8-7}$
$1=1$, получили верное равенство, следовательно, корень нам подходит.
$x_2=4$
$4-6=√{8-4}$
$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.
Ответ: $7$
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n⋅a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.
Решить уравнение $25·5^х=1$
Решение:
В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$
$5^2·5^х=5^0$
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются
$5^{2+х}=5^0$
Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели
$2+х=0$
$х=-2$
Ответ: $-2$
Решить уравнение $2^{3х+2}-2^{3х-2}=30$
Решение:
Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель
$2^{3x+2}-2^{3x-2}=30$
$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$
$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$
$2^{3x-2}(2^4-1)=30$
$2^{3x-2}·15=30$
Разделим обе части уравнения на $15$
$2^{3х-2}=2$
$2^{3х-2}=2^1$
$3х-2=1$
$3х=3$
$х=1$
Ответ: $1$
Ранее, счета за холодную воду приходили отдельно от других коммунальных услуг.
В Санкт-Петербурге было внесено изменение в систему оплаты коммунальных услуг, и теперь жители могут оплачивать свои счета за холодную воду в рамках единой квитанции за ЖКУ. Ранее, счета за холодную воду приходили отдельно от других коммунальных услуг, что иногда приводило к затруднениям и путанице у жителей города.
Это изменение внесено с целью упростить процесс оплаты коммунальных услуг и уменьшить количество счетов, которые должны получать жители. В настоящее время, жители Санкт-Петербурга могут оплачивать все свои коммунальные счета в одной единой квитанции, что существенно облегчает процесс оплаты и снижает вероятность ошибок.
Также, это изменение поможет уменьшить количество неплатежей за коммунальные услуги, так как жители смогут лучше контролировать свои расходы на ЖКУ и, возможно, смогут легче оплачивать свои счета вовремя. В целом, внедрение единой квитанции за ЖКУ в Санкт-Петербурге является положительным шагом в упрощении и улучшении процесса оплаты коммунальных услуг для жителей города.
#Марина Цурикова#2#Общество#Город и горожане
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
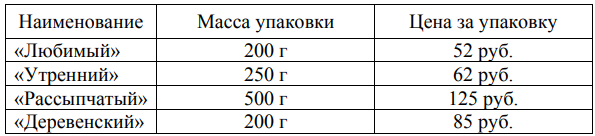
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
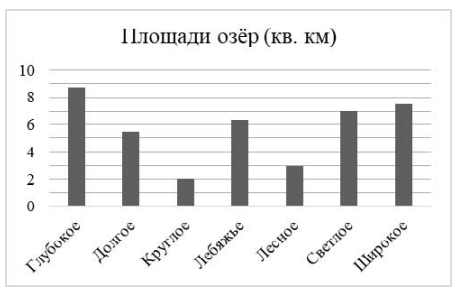
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
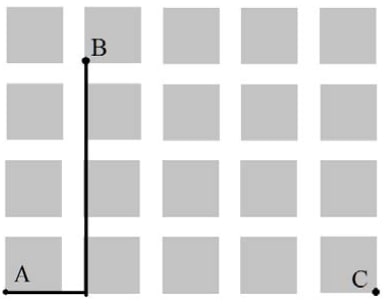
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.