Задания
Версия для печати и копирования в MS Word
Тип 10 № 564194
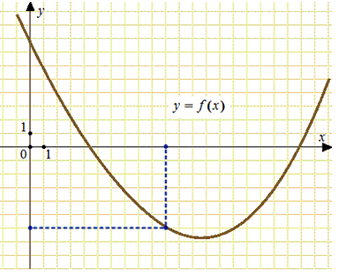
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
Спрятать решение
Решение.
В любом из случаев раскрытия модуля получаем линейную функцию
где угловой коэффициент
или
а свободный член
или
Очевидно, что
значит, большему значению углового коэффициента соответствует
а меньшему —
Аналогично большему значению свободного члена соответствует
а меньшему —
По рисунку определяем, что
Значит,
Решим уравнение
Ответ: −2.
Аналоги к заданию № 564188: 564191 564193 564194 564195 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
9
задание
ПРОФИЛЬ
ЕГЭ математика
1
вариант
1. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения
2.
На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите абсциссу вершины параболы.
3. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
4. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение x, при котором
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
7. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
10. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
9
задание
ПРОФИЛЬ
ЕГЭ математика
2
вариант
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите значение .
2. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите c.
4. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
7. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9.
На рисунке изображён график функции вида где
числа a, b и c — целые. Найдите
10. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
9
задание
ПРОФИЛЬ
ЕГЭ математика
3
вариант
1. 
функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
2. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
4. 
изображён график функции вида где
числа a, b и c — целые. Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
6. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
7. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
10. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
9
задание
ПРОФИЛЬ
ЕГЭ математика
4
вариант
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите c.
2. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
4. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6.
На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите абсциссу вершины параболы.
7. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
8. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
9. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
10. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение x, при котором
Ответы
9
задание
ПРОФИЛЬ
ЕГЭ математика
1
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
563824 |
1 |
|
2 |
564655 |
4 |
|
3 |
564586 |
2,5 |
|
4 |
564974 |
2,75 |
|
5 |
564208 |
-2,25 |
|
6 |
564160 |
2 |
|
7 |
562285 |
19 |
|
8 |
562157 |
-7 |
|
9 |
564971 |
11 |
|
10 |
564195 |
2,5 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
2
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
562153 |
-4,25 |
|
2 |
564189 |
2 |
|
3 |
564967 |
-5 |
|
4 |
564578 |
1 |
|
5 |
564201 |
-3,625 |
|
6 |
564187 |
-0,5 |
|
7 |
562292 |
44 |
|
8 |
562158 |
9,875 |
|
9 |
564650 |
1,25 |
|
10 |
564554 |
0 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
3 вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
564187 |
-0,5 |
|
2 |
564586 |
2,5 |
|
3 |
562293 |
8 |
|
4 |
564210 |
-2,75 |
|
5 |
564969 |
-5 |
|
6 |
562282 |
4,75 |
|
7 |
564194 |
-2 |
|
8 |
562154 |
-34 |
|
9 |
564587 |
-0,5 |
|
10 |
564970 |
-13 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
4
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
564966 |
2 |
|
2 |
564184 |
2,5 |
|
3 |
562162 |
11 |
|
4 |
564554 |
0 |
|
5 |
564205 |
-1,6 |
|
6 |
564657 |
-4 |
|
7 |
564193 |
5 |
|
8 |
564585 |
2 |
|
9 |
562061 |
8 |
|
10 |
564972 |
-3 |
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 9
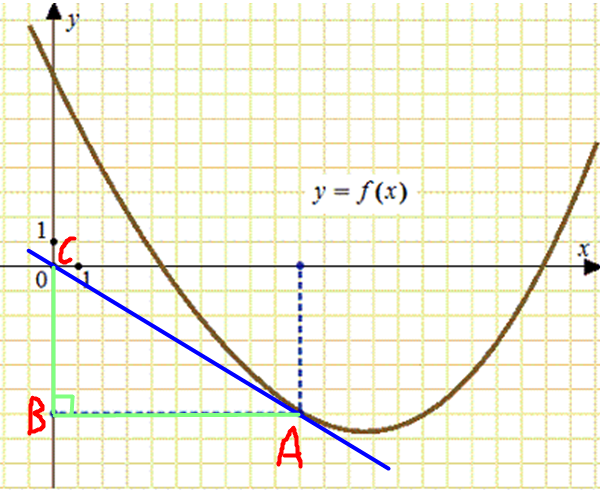
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим прямую, проходящую через начала координат (left( {0;,0} right)) и точку (left( {10;, — 6} right)), а также прямоугольный треугольник с вершинами в точках (Aleft( {10;, — 6} right),,,Bleft( {0;, — 6} right),,,Cleft( {0;,0} right)) (см. рисунок). Угол наклона касательной к оси абсцисс будет равен углу, смежному углу CAB. Поэтому:
(f’left( {{x_0}} right) = {rm{tg}}left( {{{180}^circ } — angle CAB} right) = — {rm{tg}}angle CAB = — frac{{CB}}{{AB}} = — frac{6}{{10}} = — 0,6.)
Ответ: –0,6.
9
задание
ПРОФИЛЬ
ЕГЭ математика
1
вариант
1. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения
2.
На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите абсциссу вершины параболы.
3. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
4. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение x, при котором
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
7. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
10. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
9
задание
ПРОФИЛЬ
ЕГЭ математика
2
вариант
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите значение .
2. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите c.
4. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
7. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9.
На рисунке изображён график функции вида где
числа a, b и c — целые. Найдите
10. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
9
задание
ПРОФИЛЬ
ЕГЭ математика
3
вариант
1. 
функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
2. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
4. 
изображён график функции вида где
числа a, b и c — целые. Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
6. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
7. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
10. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
9
задание
ПРОФИЛЬ
ЕГЭ математика
4
вариант
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите c.
2. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
4. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6.
На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите абсциссу вершины параболы.
7. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
8. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
9. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
10. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение x, при котором
Ответы
9
задание
ПРОФИЛЬ
ЕГЭ математика
1
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
563824 |
1 |
|
2 |
564655 |
4 |
|
3 |
564586 |
2,5 |
|
4 |
564974 |
2,75 |
|
5 |
564208 |
-2,25 |
|
6 |
564160 |
2 |
|
7 |
562285 |
19 |
|
8 |
562157 |
-7 |
|
9 |
564971 |
11 |
|
10 |
564195 |
2,5 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
2
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
562153 |
-4,25 |
|
2 |
564189 |
2 |
|
3 |
564967 |
-5 |
|
4 |
564578 |
1 |
|
5 |
564201 |
-3,625 |
|
6 |
564187 |
-0,5 |
|
7 |
562292 |
44 |
|
8 |
562158 |
9,875 |
|
9 |
564650 |
1,25 |
|
10 |
564554 |
0 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
3 вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
564187 |
-0,5 |
|
2 |
564586 |
2,5 |
|
3 |
562293 |
8 |
|
4 |
564210 |
-2,75 |
|
5 |
564969 |
-5 |
|
6 |
562282 |
4,75 |
|
7 |
564194 |
-2 |
|
8 |
562154 |
-34 |
|
9 |
564587 |
-0,5 |
|
10 |
564970 |
-13 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
4
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
564966 |
2 |
|
2 |
564184 |
2,5 |
|
3 |
562162 |
11 |
|
4 |
564554 |
0 |
|
5 |
564205 |
-1,6 |
|
6 |
564657 |
-4 |
|
7 |
564193 |
5 |
|
8 |
564585 |
2 |
|
9 |
562061 |
8 |
|
10 |
564972 |
-3 |
На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 564972?
На число 564972 без остатка (нацело) делятся следующие числа: 564972, 1129944, 1694916, 2259888, 2824860, 3389832, 3954804, 4519776, 5084748, 5649720, 6214692, 6779664 и многие другие.
Какие четные числа делятся на 564972?
На число 564972 делятся следующие четные числа: 564972, 1129944, 1694916, 2259888, 2824860, 3389832, 3954804, 4519776, 5084748, 5649720, 6214692, 6779664 и многие други.
Какие нечетные числа делятся на 564972?
Таких чисел нет
На какое наибольшее число делится число 564972 без остатка?
Наибольшее число на которое делится число 564972 есть само число 564972. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 564972 без остатка, не считая числа 564972 и 1?
Наибольшим делителем числа 564972 не считая самого числа 564972 является число 282486.
Какое наименьшее натуральное число делится на 564972?
Наименьшее натуральное число которое делиться на число 564972 является само число 564972.
На какое наименьшее натуральное число делится число 564972?
Наименьшее натуральное число на которое можно разделить число 564972 — это число 1.
(что бы не забыть запишите все делители числа 564972 в блокнот.)На какие целые и(или) натуральные числа делится число 564972?
Число 564972 делится на следующие целые, натуральные числа (все делители числа 564972): 1, 2, 3, 4, 6, 12, 23, 46, 69, 89, 92, 138, 178, 267, 276, 356, 529, 534, 1058, 1068, 1587, 2047, 2116, 3174, 4094, 6141, 6348, 8188, 12282, 24564, 47081, 94162, 141243, 188324, 282486, 564972
На какие четные числа делится число 564972?
Число 564972 делится на следующие четные числа (четные делители числа): 2, 4, 6, 12, 46, 92, 138, 178, 276, 356, 534, 1058, 1068, 2116, 3174, 4094, 6348, 8188, 12282, 24564, 94162, 188324, 282486, 564972
На какие нечетные числа делится число 564972?
Число 564972 делится на следующие нечетные числа (нечетные делители числа): 1, 3, 23, 69, 89, 267, 529, 1587, 2047, 6141, 47081, 141243
Сколько делителей имеет число 564972?
Число 564972 имеет 36 делителей
Сколько четных делителей имеет число 564972?
Число 564972 имеет 24 четных делителя
Сколько нечетных делителей имеет число 564972?
Число 564972 имеет 12 нечетных делителей
Число 564972 прописью, словами.
— пятьсот шестьдесят четыре тысячи девятьсот семьдесят два
(что бы не забыть запишите число 564972 прописью в блокнот.)
Числа кратные 564972.
— кратные числа, числу 564972 : 1129944, 1694916, 2259888, 2824860, 3389832, 3954804, 4519776, 5084748, 5649720, 6214692, 6779664 и многие другие.
Простые множители числа 564972.
У числа 564972 нет простых множителей кроме 1.
Сумма цифр числа 564972.
Сумма цифр числа 564972 равна 33
Произведение цифр числа 564972.
Произведение цифр числа 564972 равна 15120
Квадрат числа 564972.
Квадрат числа 564972 равен 319193360784
Куб числа 564972.
Куб числа 564972 равен 180335311428858048
Квадратный корень числа 564972.
Квадратный корень числа 564972 равен 751.6461.
Число 564972 в двоичной системе счисления.
Запись числа 564972 в двоичной системе счисления выглядит так: 10001001111011101100
Количество значащих нулей в двоичной записи числа 564972 = 9
Количество едениц в двоичной записи числа 564972 = 11
(что бы не забыть запишите число 564972 в двоичной системе счисления в блокнот.)Число 564972 в шестнадцатеричной системе счисления.
Запись числа 564972 в шестнадцатеричной системе счисления выглядит так: 89eec
(что бы не забыть запишите число 564972 в шестнадцатеричной системе счисления в блокнот.)Число 564972 в восьмеричной системе счисления.
Запись числа 564972 в восьмеричной системе счисления выглядит так: 2117354
(что бы не забыть запишите число 564972 в восьмеричной системе счисления в блокнот.)Число 564972 не является простым!
Корни числа 564972.
Корень 3 степени из 564972.
Корень 3 (третьей) степени из 564972 равен 82.66892842696
Корень 4 степени из 564972.
Корень 4 (четвертой) степени из 564972 равен 27.41616664242
Корень 5 степени из 564972.
Корень 5 (пятой) степени из 564972 равен 14.138566698123
Корень 6 степени из 564972.
Корень 6 (шестой) степени из 564972 равен 9.0922455107064
Корень 7 степени из 564972.
Корень 7 (седьмой) степени из 564972 равен 6.633124244431
Корень 8 степени из 564972.
Корень 8 (восьмой) степени из 564972 равен 5.2360449427426
Корень 9 степени из 564972.
Корень 9 (девятой) степени из 564972 равен 4.3562631131252
Корень 10 степени из 564972.
Корень 10 (десятой) степени из 564972 равен 3.7601285480849
Корень 11 степени из 564972.
Корень 11 (одиннадцатой) степени из 564972 равен 3.3335850409555
Корень 12 степени из 564972.
Корень 12 (двенадцатой) степени из 564972 равен 3.0153350577849
Корень 13 степени из 564972.
Корень 13 (тринадцатой) степени из 564972 равен 2.7698969342208
Корень 14 степени из 564972.
Корень 14 (четырнадцатой) степени из 564972 равен 2.57548524446
Корень 15 степени из 564972.
Корень 15 (пятнадцатой) степени из 564972 равен 2.4180677321091
Степени числа 564972.
564972 в 3 степени.
564972 в 3 степени равно 180335311428858048.
564972 в 4 степени.
564972 в 4 степени равно 1.0188440156858E+23.
564972 в 5 степени.
564972 в 5 степени равно 5.7561834123006E+28.
564972 в 6 степени.
564972 в 6 степени равно 3.2520824548143E+34.
564972 в 7 степени.
564972 в 7 степени равно 1.8373355286614E+40.
564972 в 8 степени.
564972 в 8 степени равно 1.0380431282989E+46.
564972 в 9 степени.
564972 в 9 степени равно 5.8646530228127E+51.
564972 в 10 степени.
564972 в 10 степени равно 3.3133647476045E+57.
564972 в 11 степени.
564972 в 11 степени равно 1.8719583081836E+63.
564972 в 12 степени.
564972 в 12 степени равно 1.0576040292911E+69.
564972 в 13 степени.
564972 в 13 степени равно 5.9751666363666E+74.
564972 в 14 степени.
564972 в 14 степени равно 3.3758018448813E+80.
564972 в 15 степени.
564972 в 15 степени равно 1.9072335199063E+86.
Какое число имеет такую же сумму цифр как и число 564972?Математика. Найти сумму цифр числа 564972.
Число 564972 состоит из следующих цифр — 5, 6, 4, 9, 7, 2.
Определить сумму цифр числа 564972 не так уж и сложно.
Сумма цифр шестизначного числа 564972 равна 5 + 6 + 4 + 9 + 7 + 2 = 33.
Числа сумма цифр которых равна 33.
Следующие числа имеют такую же сумму цифр как и число 564972 — 6999, 7899, 7989, 7998, 8799, 8889, 8898, 8979, 8988, 8997, 9699, 9789, 9798, 9879, 9888, 9897, 9969, 9978, 9987, 9996.
Четырехзначные числа сумма цифр которых равна 33 — 6999, 7899, 7989, 7998, 8799, 8889, 8898, 8979, 8988, 8997.
Пятизначные числа сумма цифр которых равна 33 — 15999, 16899, 16989, 16998, 17799, 17889, 17898, 17979, 17988, 17997.
Шестизначные числа сумма цифр которых равна 33 — 105999, 106899, 106989, 106998, 107799, 107889, 107898, 107979, 107988, 107997.
Квадрат суммы цифр числа 564972.
Квадрат суммы цифр шестизначного числа 564972 равен 5 + 6 + 4 + 9 + 7 + 2 = 33² = 1089.
Сумма квадратов цифр шестизначного числа 564972.
Сумма квадратов цифр числа 564972 равна 5² + 6² + 4² + 9² + 7² + 2² = 25 + 36 + 16 + 81 + 49 + 4 = 211.
Сумма четных цифр числа 564972.
Сумма четных цифр шестизначного числа 564972 равна 6 + 4 + 2 = 12.
Квадрат суммы четных цифр шестизначного числа 564972.
Квадрат суммы четных цифр числа 564972 равна 6 + 4 + 2 = 12² = 144.
Сумма квадратов четных цифр шестизначного числа 564972.
Сумма квадратов четных цифр числа 564972 равна 6² + 4² + 2² = 36 + 16 + 4 = 56.
Сумма нечетных цифр числа 564972.
Сумма нечетных цифр шестизначного числа 564972 равна 5 + 9 + 7 = 21.
Квадрат суммы нечетных цифр шестизначного числа 564972.
Квадрат суммы нечетных цифр числа 564972 равна 5 + 9 + 7 = 21² = 441.
Сумма квадратов нечетных цифр шестизначного числа 564972.
Сумма квадратов нечетных цифр числа 564972 равна 5² + 9² + 7² = 25 + 81 + 49 = 155.
Произведение цифр числа 564972.
Какое число имеет такое же произведение цифр как и число 564972?Математика. Найти произведение цифр числа 564972.
Число 564972 состоит из следующих цифр — 5, 6, 4, 9, 7, 2.
Найти сумму цифр числа 564972 просто.
Решение:
Произведение цифр числа 564972 равно 5 * 6 * 4 * 9 * 7 * 2 = 15120.
Числа произведение цифр которых равно 15120.
Следующие числа имеют такое же произведение цифр как и число 564972 — 56789, 56798, 56879, 56897, 56978, 56987, 57689, 57698, 57869, 57896, 57968, 57986, 58679, 58697, 58769, 58796, 58967, 58976, 59678, 59687.
Пятизначные числа произведение цифр которых равно 15120 — 56789, 56798, 56879, 56897, 56978, 56987, 57689, 57698, 57869, 57896.
Шестизначные числа произведение цифр которых равно 15120 — 156789, 156798, 156879, 156897, 156978, 156987, 157689, 157698, 157869, 157896.
Квадрат произведения цифр числа 564972.
Квадрат произведения цифр шестизначного числа 564972 равен 5 * 6 * 4 * 9 * 7 * 2 = 15120² = 228614400.
Произведение квадратов цифр шестизначного числа 564972.
Произведение квадратов цифр числа 564972 равна 5² * 6² * 4² * 9² * 7² * 2² = 25 * 36 * 16 * 81 * 49 * 4 = 228614400.
Произведение четных цифр числа 564972.
Произведение четных цифр шестизначного числа 564972 равно 6 * 4 * 2 = 48.
Квадрат произведения четных цифр шестизначного числа 564972.
Квадрат произведения четных цифр числа 564972 равен 6 * 4 * 2 = 48² = 2304.
Произведение квадратов четных цифр шестизначного числа 564972.
Произведение квадратов четных цифр числа 564972 равно 6² * 4² * 2² = 36 * 16 * 4 = 2304.
Произведение нечетных цифр числа 564972.
Произведение нечетных цифр шестизначного числа 564972 равно 5 * 9 * 7 = 315.
Квадрат произведения нечетных цифр шестизначного числа 564972.
Квадрат произведения нечетных цифр числа 564972 равен 5 * 9 * 7 = 315² = 99225.
Произведение квадратов нечетных цифр шестизначного числа 564972.
Произведение квадратов нечетных цифр числа 564972 равно 5² * 9² * 7² = 25 * 81 * 49 = 99225.
Запишите числа которые в сумме дают число 564972.
Задача: Данно число 564972.Какие 2(два) числа дают в сумме число 564972?Решение:
1) 257202 + 307770 = 564972
2) 180317 + 384655 = 564972
3) 128515 + 436457 = 564972
4) 54834 + 510138 = 564972
5) 73963 + 491009 = 564972
Какие 3(три) числа дают в сумме число 564972?Решение:
1) 60174 + 228879 + 275919 = 564972
2) 30641 + 4318 + 530013 = 564972
3) 169161 + 15339 + 380472 = 564972
4) 703 + 138624 + 425645 = 564972
5) 138724 + 169721 + 256527 = 564972
Какие 4(четыре) числа дают в сумме число 564972?Решение:
1) 116722 + 60034 + 35725 + 352491 = 564972
2) 23475 + 86682 + 1233 + 453582 = 564972
3) 2409 + 133244 + 28692 + 400627 = 564972
4) 49923 + 136258 + 140151 + 238640 = 564972
5) 22790 + 102876 + 207710 + 231596 = 564972
Какие 5(пять) чисел дают в сумме число 564972?Решение:
1) 8408 + 137381 + 131961 + 98949 + 188273 = 564972
2) 62390 + 124251 + 162756 + 38536 + 177039 = 564972
3) 81466 + 91757 + 55800 + 98011 + 237938 = 564972
4) 81416 + 87456 + 141473 + 97483 + 157144 = 564972
5) 10817 + 81986 + 92386 + 151188 + 228595 = 564972
Разделите число 564972 на 2 части в отношении 1:2 без остатка.Решение:
Расчитаем количество частей: 1 + 2 = 3
Узнаем размер одной части: 564972 : 3 = 188324
1 * 188324 = 188324
2 * 188324 = 376648
Ответ: Результатом деления числа 564972 на две части в отношении 1:2 являются числа 188324 и 376648.
Проверка: 188324 + 376648 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 2 к 1 будут те же числа 188324 и 376648
Разделите число 564972 на 2 части в отношении 1:3 без остатка.Решение:
Расчитаем количество частей: 1 + 3 = 4
Узнаем размер одной части: 564972 : 4 = 141243
1 * 141243 = 141243
3 * 141243 = 423729
Ответ: Результатом деления числа 564972 на две части в отношении 1:3 являются числа 141243 и 423729.
Проверка: 141243 + 423729 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 3 к 1 будут те же числа 141243 и 423729
Разделите число 564972 на 2 части в отношении 1:5 без остатка.Решение:
Расчитаем количество частей: 1 + 5 = 6
Узнаем размер одной части: 564972 : 6 = 94162
1 * 94162 = 94162
5 * 94162 = 470810
Ответ: Результатом деления числа 564972 на две части в отношении 1:5 являются числа 94162 и 470810.
Проверка: 94162 + 470810 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 5 к 1 будут те же числа 94162 и 470810
Разделите число 564972 на 2 части в отношении 2:2 без остатка.Решение:
Расчитаем количество частей: 2 + 2 = 4
Узнаем размер одной части: 564972 : 4 = 141243
2 * 141243 = 282486
2 * 141243 = 282486
Ответ: Результатом деления числа 564972 на две части в отношении 2:2 являются числа 282486 и 282486.
Проверка: 282486 + 282486 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 2 к 2 будут те же числа 282486 и 282486
Разделите число 564972 на 2 части в отношении 2:4 без остатка.Решение:
Расчитаем количество частей: 2 + 4 = 6
Узнаем размер одной части: 564972 : 6 = 94162
2 * 94162 = 188324
4 * 94162 = 376648
Ответ: Результатом деления числа 564972 на две части в отношении 2:4 являются числа 188324 и 376648.
Проверка: 188324 + 376648 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 4 к 2 будут те же числа 188324 и 376648
Разделите число 564972 на 2 части в отношении 3:3 без остатка.Решение:
Расчитаем количество частей: 3 + 3 = 6
Узнаем размер одной части: 564972 : 6 = 94162
3 * 94162 = 282486
3 * 94162 = 282486
Ответ: Результатом деления числа 564972 на две части в отношении 3:3 являются числа 282486 и 282486.
Проверка: 282486 + 282486 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 3 к 3 будут те же числа 282486 и 282486
Разделите число 564972 на 2 части в отношении 3:9 без остатка.Решение:
Расчитаем количество частей: 3 + 9 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
9 * 47081 = 423729
Ответ: Результатом деления числа 564972 на две части в отношении 3:9 являются числа 141243 и 423729.
Проверка: 141243 + 423729 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 9 к 3 будут те же числа 141243 и 423729
Разделите число 564972 на 2 части в отношении 4:2 без остатка.Решение:
Расчитаем количество частей: 4 + 2 = 6
Узнаем размер одной части: 564972 : 6 = 94162
4 * 94162 = 376648
2 * 94162 = 188324
Ответ: Результатом деления числа 564972 на две части в отношении 4:2 являются числа 376648 и 188324.
Проверка: 376648 + 188324 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 2 к 4 будут те же числа 376648 и 188324
Разделите число 564972 на 2 части в отношении 4:8 без остатка.Решение:
Расчитаем количество частей: 4 + 8 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
8 * 47081 = 376648
Ответ: Результатом деления числа 564972 на две части в отношении 4:8 являются числа 188324 и 376648.
Проверка: 188324 + 376648 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 8 к 4 будут те же числа 188324 и 376648
Разделите число 564972 на 2 части в отношении 5:7 без остатка.Решение:
Расчитаем количество частей: 5 + 7 = 12
Узнаем размер одной части: 564972 : 12 = 47081
5 * 47081 = 235405
7 * 47081 = 329567
Ответ: Результатом деления числа 564972 на две части в отношении 5:7 являются числа 235405 и 329567.
Проверка: 235405 + 329567 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 7 к 5 будут те же числа 235405 и 329567
Разделите число 564972 на 2 части в отношении 6:6 без остатка.Решение:
Расчитаем количество частей: 6 + 6 = 12
Узнаем размер одной части: 564972 : 12 = 47081
6 * 47081 = 282486
6 * 47081 = 282486
Ответ: Результатом деления числа 564972 на две части в отношении 6:6 являются числа 282486 и 282486.
Проверка: 282486 + 282486 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 6 к 6 будут те же числа 282486 и 282486
Разделите число 564972 на 2 части в отношении 7:5 без остатка.Решение:
Расчитаем количество частей: 7 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
7 * 47081 = 329567
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на две части в отношении 7:5 являются числа 329567 и 235405.
Проверка: 329567 + 235405 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 5 к 7 будут те же числа 329567 и 235405
Разделите число 564972 на 2 части в отношении 8:4 без остатка.Решение:
Расчитаем количество частей: 8 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
8 * 47081 = 376648
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на две части в отношении 8:4 являются числа 376648 и 188324.
Проверка: 376648 + 188324 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 4 к 8 будут те же числа 376648 и 188324
Разделите число 564972 на 2 части в отношении 9:3 без остатка.Решение:
Расчитаем количество частей: 9 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
9 * 47081 = 423729
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на две части в отношении 9:3 являются числа 423729 и 141243.
Проверка: 423729 + 141243 = 564972
Примечание: Результатом деления числа 564972 на части в отношении 3 к 9 будут те же числа 423729 и 141243
Разделите число 564972 на 3 части в отношении 1:1:2 без остатка.Решение:
Расчитаем количество частей: 1 + 1 + 2 = 4
Узнаем размер одной части: 564972 : 4 = 141243
1 * 141243 = 141243
1 * 141243 = 141243
2 * 141243 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 1:1:2 являются числа 141243 и 141243 и 282486.
Проверка: 141243 + 141243 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 1:1:4 без остатка.Решение:
Расчитаем количество частей: 1 + 1 + 4 = 6
Узнаем размер одной части: 564972 : 6 = 94162
1 * 94162 = 94162
1 * 94162 = 94162
4 * 94162 = 376648
Ответ: Результатом деления числа 564972 на три части в отношении 1:1:4 являются числа 94162 и 94162 и 376648.
Проверка: 94162 + 94162 + 376648 = 564972
Разделите число 564972 на 3 части в отношении 1:2:3 без остатка.Решение:
Расчитаем количество частей: 1 + 2 + 3 = 6
Узнаем размер одной части: 564972 : 6 = 94162
1 * 94162 = 94162
2 * 94162 = 188324
3 * 94162 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 1:2:3 являются числа 94162 и 188324 и 282486.
Проверка: 94162 + 188324 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 1:2:9 без остатка.Решение:
Расчитаем количество частей: 1 + 2 + 9 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
2 * 47081 = 94162
9 * 47081 = 423729
Ответ: Результатом деления числа 564972 на три части в отношении 1:2:9 являются числа 47081 и 94162 и 423729.
Проверка: 47081 + 94162 + 423729 = 564972
Разделите число 564972 на 3 части в отношении 1:3:2 без остатка.Решение:
Расчитаем количество частей: 1 + 3 + 2 = 6
Узнаем размер одной части: 564972 : 6 = 94162
1 * 94162 = 94162
3 * 94162 = 282486
2 * 94162 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 1:3:2 являются числа 94162 и 282486 и 188324.
Проверка: 94162 + 282486 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 1:3:8 без остатка.Решение:
Расчитаем количество частей: 1 + 3 + 8 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
3 * 47081 = 141243
8 * 47081 = 376648
Ответ: Результатом деления числа 564972 на три части в отношении 1:3:8 являются числа 47081 и 141243 и 376648.
Проверка: 47081 + 141243 + 376648 = 564972
Разделите число 564972 на 3 части в отношении 1:4:7 без остатка.Решение:
Расчитаем количество частей: 1 + 4 + 7 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
4 * 47081 = 188324
7 * 47081 = 329567
Ответ: Результатом деления числа 564972 на три части в отношении 1:4:7 являются числа 47081 и 188324 и 329567.
Проверка: 47081 + 188324 + 329567 = 564972
Разделите число 564972 на 3 части в отношении 1:5:6 без остатка.Решение:
Расчитаем количество частей: 1 + 5 + 6 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
5 * 47081 = 235405
6 * 47081 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 1:5:6 являются числа 47081 и 235405 и 282486.
Проверка: 47081 + 235405 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 1:6:5 без остатка.Решение:
Расчитаем количество частей: 1 + 6 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
6 * 47081 = 282486
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на три части в отношении 1:6:5 являются числа 47081 и 282486 и 235405.
Проверка: 47081 + 282486 + 235405 = 564972
Разделите число 564972 на 3 части в отношении 1:7:4 без остатка.Решение:
Расчитаем количество частей: 1 + 7 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
7 * 47081 = 329567
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 1:7:4 являются числа 47081 и 329567 и 188324.
Проверка: 47081 + 329567 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 1:8:3 без остатка.Решение:
Расчитаем количество частей: 1 + 8 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
8 * 47081 = 376648
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 1:8:3 являются числа 47081 и 376648 и 141243.
Проверка: 47081 + 376648 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 1:9:2 без остатка.Решение:
Расчитаем количество частей: 1 + 9 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
1 * 47081 = 47081
9 * 47081 = 423729
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 1:9:2 являются числа 47081 и 423729 и 94162.
Проверка: 47081 + 423729 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 2:1:3 без остатка.Решение:
Расчитаем количество частей: 2 + 1 + 3 = 6
Узнаем размер одной части: 564972 : 6 = 94162
2 * 94162 = 188324
1 * 94162 = 94162
3 * 94162 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 2:1:3 являются числа 188324 и 94162 и 282486.
Проверка: 188324 + 94162 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 2:1:9 без остатка.Решение:
Расчитаем количество частей: 2 + 1 + 9 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
1 * 47081 = 47081
9 * 47081 = 423729
Ответ: Результатом деления числа 564972 на три части в отношении 2:1:9 являются числа 94162 и 47081 и 423729.
Проверка: 94162 + 47081 + 423729 = 564972
Разделите число 564972 на 3 части в отношении 2:2:2 без остатка.Решение:
Расчитаем количество частей: 2 + 2 + 2 = 6
Узнаем размер одной части: 564972 : 6 = 94162
2 * 94162 = 188324
2 * 94162 = 188324
2 * 94162 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 2:2:2 являются числа 188324 и 188324 и 188324.
Проверка: 188324 + 188324 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 2:2:8 без остатка.Решение:
Расчитаем количество частей: 2 + 2 + 8 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
2 * 47081 = 94162
8 * 47081 = 376648
Ответ: Результатом деления числа 564972 на три части в отношении 2:2:8 являются числа 94162 и 94162 и 376648.
Проверка: 94162 + 94162 + 376648 = 564972
Разделите число 564972 на 3 части в отношении 2:3:7 без остатка.Решение:
Расчитаем количество частей: 2 + 3 + 7 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
3 * 47081 = 141243
7 * 47081 = 329567
Ответ: Результатом деления числа 564972 на три части в отношении 2:3:7 являются числа 94162 и 141243 и 329567.
Проверка: 94162 + 141243 + 329567 = 564972
Разделите число 564972 на 3 части в отношении 2:4:6 без остатка.Решение:
Расчитаем количество частей: 2 + 4 + 6 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
4 * 47081 = 188324
6 * 47081 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 2:4:6 являются числа 94162 и 188324 и 282486.
Проверка: 94162 + 188324 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 2:5:5 без остатка.Решение:
Расчитаем количество частей: 2 + 5 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
5 * 47081 = 235405
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на три части в отношении 2:5:5 являются числа 94162 и 235405 и 235405.
Проверка: 94162 + 235405 + 235405 = 564972
Разделите число 564972 на 3 части в отношении 2:6:4 без остатка.Решение:
Расчитаем количество частей: 2 + 6 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
6 * 47081 = 282486
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 2:6:4 являются числа 94162 и 282486 и 188324.
Проверка: 94162 + 282486 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 2:7:3 без остатка.Решение:
Расчитаем количество частей: 2 + 7 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
7 * 47081 = 329567
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 2:7:3 являются числа 94162 и 329567 и 141243.
Проверка: 94162 + 329567 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 2:8:2 без остатка.Решение:
Расчитаем количество частей: 2 + 8 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
2 * 47081 = 94162
8 * 47081 = 376648
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 2:8:2 являются числа 94162 и 376648 и 94162.
Проверка: 94162 + 376648 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 3:1:2 без остатка.Решение:
Расчитаем количество частей: 3 + 1 + 2 = 6
Узнаем размер одной части: 564972 : 6 = 94162
3 * 94162 = 282486
1 * 94162 = 94162
2 * 94162 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 3:1:2 являются числа 282486 и 94162 и 188324.
Проверка: 282486 + 94162 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 3:1:8 без остатка.Решение:
Расчитаем количество частей: 3 + 1 + 8 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
1 * 47081 = 47081
8 * 47081 = 376648
Ответ: Результатом деления числа 564972 на три части в отношении 3:1:8 являются числа 141243 и 47081 и 376648.
Проверка: 141243 + 47081 + 376648 = 564972
Разделите число 564972 на 3 части в отношении 3:2:7 без остатка.Решение:
Расчитаем количество частей: 3 + 2 + 7 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
2 * 47081 = 94162
7 * 47081 = 329567
Ответ: Результатом деления числа 564972 на три части в отношении 3:2:7 являются числа 141243 и 94162 и 329567.
Проверка: 141243 + 94162 + 329567 = 564972
Разделите число 564972 на 3 части в отношении 3:3:6 без остатка.Решение:
Расчитаем количество частей: 3 + 3 + 6 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
3 * 47081 = 141243
6 * 47081 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 3:3:6 являются числа 141243 и 141243 и 282486.
Проверка: 141243 + 141243 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 3:4:5 без остатка.Решение:
Расчитаем количество частей: 3 + 4 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
4 * 47081 = 188324
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на три части в отношении 3:4:5 являются числа 141243 и 188324 и 235405.
Проверка: 141243 + 188324 + 235405 = 564972
Разделите число 564972 на 3 части в отношении 3:5:4 без остатка.Решение:
Расчитаем количество частей: 3 + 5 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
5 * 47081 = 235405
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 3:5:4 являются числа 141243 и 235405 и 188324.
Проверка: 141243 + 235405 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 3:6:3 без остатка.Решение:
Расчитаем количество частей: 3 + 6 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
6 * 47081 = 282486
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 3:6:3 являются числа 141243 и 282486 и 141243.
Проверка: 141243 + 282486 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 3:7:2 без остатка.Решение:
Расчитаем количество частей: 3 + 7 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
3 * 47081 = 141243
7 * 47081 = 329567
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 3:7:2 являются числа 141243 и 329567 и 94162.
Проверка: 141243 + 329567 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 4:1:7 без остатка.Решение:
Расчитаем количество частей: 4 + 1 + 7 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
1 * 47081 = 47081
7 * 47081 = 329567
Ответ: Результатом деления числа 564972 на три части в отношении 4:1:7 являются числа 188324 и 47081 и 329567.
Проверка: 188324 + 47081 + 329567 = 564972
Разделите число 564972 на 3 части в отношении 4:2:6 без остатка.Решение:
Расчитаем количество частей: 4 + 2 + 6 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
2 * 47081 = 94162
6 * 47081 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 4:2:6 являются числа 188324 и 94162 и 282486.
Проверка: 188324 + 94162 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 4:3:5 без остатка.Решение:
Расчитаем количество частей: 4 + 3 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
3 * 47081 = 141243
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на три части в отношении 4:3:5 являются числа 188324 и 141243 и 235405.
Проверка: 188324 + 141243 + 235405 = 564972
Разделите число 564972 на 3 части в отношении 4:4:4 без остатка.Решение:
Расчитаем количество частей: 4 + 4 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
4 * 47081 = 188324
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 4:4:4 являются числа 188324 и 188324 и 188324.
Проверка: 188324 + 188324 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 4:5:3 без остатка.Решение:
Расчитаем количество частей: 4 + 5 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
5 * 47081 = 235405
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 4:5:3 являются числа 188324 и 235405 и 141243.
Проверка: 188324 + 235405 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 4:6:2 без остатка.Решение:
Расчитаем количество частей: 4 + 6 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
4 * 47081 = 188324
6 * 47081 = 282486
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 4:6:2 являются числа 188324 и 282486 и 94162.
Проверка: 188324 + 282486 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 5:1:6 без остатка.Решение:
Расчитаем количество частей: 5 + 1 + 6 = 12
Узнаем размер одной части: 564972 : 12 = 47081
5 * 47081 = 235405
1 * 47081 = 47081
6 * 47081 = 282486
Ответ: Результатом деления числа 564972 на три части в отношении 5:1:6 являются числа 235405 и 47081 и 282486.
Проверка: 235405 + 47081 + 282486 = 564972
Разделите число 564972 на 3 части в отношении 5:2:5 без остатка.Решение:
Расчитаем количество частей: 5 + 2 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
5 * 47081 = 235405
2 * 47081 = 94162
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на три части в отношении 5:2:5 являются числа 235405 и 94162 и 235405.
Проверка: 235405 + 94162 + 235405 = 564972
Разделите число 564972 на 3 части в отношении 5:3:4 без остатка.Решение:
Расчитаем количество частей: 5 + 3 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
5 * 47081 = 235405
3 * 47081 = 141243
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 5:3:4 являются числа 235405 и 141243 и 188324.
Проверка: 235405 + 141243 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 5:4:3 без остатка.Решение:
Расчитаем количество частей: 5 + 4 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
5 * 47081 = 235405
4 * 47081 = 188324
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 5:4:3 являются числа 235405 и 188324 и 141243.
Проверка: 235405 + 188324 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 5:5:2 без остатка.Решение:
Расчитаем количество частей: 5 + 5 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
5 * 47081 = 235405
5 * 47081 = 235405
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 5:5:2 являются числа 235405 и 235405 и 94162.
Проверка: 235405 + 235405 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 5:9:9 без остатка.Решение:
Расчитаем количество частей: 5 + 9 + 9 = 23
Узнаем размер одной части: 564972 : 23 = 24564
5 * 24564 = 122820
9 * 24564 = 221076
9 * 24564 = 221076
Ответ: Результатом деления числа 564972 на три части в отношении 5:9:9 являются числа 122820 и 221076 и 221076.
Проверка: 122820 + 221076 + 221076 = 564972
Разделите число 564972 на 3 части в отношении 6:1:5 без остатка.Решение:
Расчитаем количество частей: 6 + 1 + 5 = 12
Узнаем размер одной части: 564972 : 12 = 47081
6 * 47081 = 282486
1 * 47081 = 47081
5 * 47081 = 235405
Ответ: Результатом деления числа 564972 на три части в отношении 6:1:5 являются числа 282486 и 47081 и 235405.
Проверка: 282486 + 47081 + 235405 = 564972
Разделите число 564972 на 3 части в отношении 6:2:4 без остатка.Решение:
Расчитаем количество частей: 6 + 2 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
6 * 47081 = 282486
2 * 47081 = 94162
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 6:2:4 являются числа 282486 и 94162 и 188324.
Проверка: 282486 + 94162 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 6:3:3 без остатка.Решение:
Расчитаем количество частей: 6 + 3 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
6 * 47081 = 282486
3 * 47081 = 141243
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 6:3:3 являются числа 282486 и 141243 и 141243.
Проверка: 282486 + 141243 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 6:4:2 без остатка.Решение:
Расчитаем количество частей: 6 + 4 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
6 * 47081 = 282486
4 * 47081 = 188324
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 6:4:2 являются числа 282486 и 188324 и 94162.
Проверка: 282486 + 188324 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 6:8:9 без остатка.Решение:
Расчитаем количество частей: 6 + 8 + 9 = 23
Узнаем размер одной части: 564972 : 23 = 24564
6 * 24564 = 147384
8 * 24564 = 196512
9 * 24564 = 221076
Ответ: Результатом деления числа 564972 на три части в отношении 6:8:9 являются числа 147384 и 196512 и 221076.
Проверка: 147384 + 196512 + 221076 = 564972
Разделите число 564972 на 3 части в отношении 6:9:8 без остатка.Решение:
Расчитаем количество частей: 6 + 9 + 8 = 23
Узнаем размер одной части: 564972 : 23 = 24564
6 * 24564 = 147384
9 * 24564 = 221076
8 * 24564 = 196512
Ответ: Результатом деления числа 564972 на три части в отношении 6:9:8 являются числа 147384 и 221076 и 196512.
Проверка: 147384 + 221076 + 196512 = 564972
Разделите число 564972 на 3 части в отношении 7:1:4 без остатка.Решение:
Расчитаем количество частей: 7 + 1 + 4 = 12
Узнаем размер одной части: 564972 : 12 = 47081
7 * 47081 = 329567
1 * 47081 = 47081
4 * 47081 = 188324
Ответ: Результатом деления числа 564972 на три части в отношении 7:1:4 являются числа 329567 и 47081 и 188324.
Проверка: 329567 + 47081 + 188324 = 564972
Разделите число 564972 на 3 части в отношении 7:2:3 без остатка.Решение:
Расчитаем количество частей: 7 + 2 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
7 * 47081 = 329567
2 * 47081 = 94162
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 7:2:3 являются числа 329567 и 94162 и 141243.
Проверка: 329567 + 94162 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 7:3:2 без остатка.Решение:
Расчитаем количество частей: 7 + 3 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
7 * 47081 = 329567
3 * 47081 = 141243
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 7:3:2 являются числа 329567 и 141243 и 94162.
Проверка: 329567 + 141243 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 7:7:9 без остатка.Решение:
Расчитаем количество частей: 7 + 7 + 9 = 23
Узнаем размер одной части: 564972 : 23 = 24564
7 * 24564 = 171948
7 * 24564 = 171948
9 * 24564 = 221076
Ответ: Результатом деления числа 564972 на три части в отношении 7:7:9 являются числа 171948 и 171948 и 221076.
Проверка: 171948 + 171948 + 221076 = 564972
Разделите число 564972 на 3 части в отношении 7:8:8 без остатка.Решение:
Расчитаем количество частей: 7 + 8 + 8 = 23
Узнаем размер одной части: 564972 : 23 = 24564
7 * 24564 = 171948
8 * 24564 = 196512
8 * 24564 = 196512
Ответ: Результатом деления числа 564972 на три части в отношении 7:8:8 являются числа 171948 и 196512 и 196512.
Проверка: 171948 + 196512 + 196512 = 564972
Разделите число 564972 на 3 части в отношении 7:9:7 без остатка.Решение:
Расчитаем количество частей: 7 + 9 + 7 = 23
Узнаем размер одной части: 564972 : 23 = 24564
7 * 24564 = 171948
9 * 24564 = 221076
7 * 24564 = 171948
Ответ: Результатом деления числа 564972 на три части в отношении 7:9:7 являются числа 171948 и 221076 и 171948.
Проверка: 171948 + 221076 + 171948 = 564972
Разделите число 564972 на 3 части в отношении 8:1:3 без остатка.Решение:
Расчитаем количество частей: 8 + 1 + 3 = 12
Узнаем размер одной части: 564972 : 12 = 47081
8 * 47081 = 376648
1 * 47081 = 47081
3 * 47081 = 141243
Ответ: Результатом деления числа 564972 на три части в отношении 8:1:3 являются числа 376648 и 47081 и 141243.
Проверка: 376648 + 47081 + 141243 = 564972
Разделите число 564972 на 3 части в отношении 8:2:2 без остатка.Решение:
Расчитаем количество частей: 8 + 2 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
8 * 47081 = 376648
2 * 47081 = 94162
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 8:2:2 являются числа 376648 и 94162 и 94162.
Проверка: 376648 + 94162 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 8:6:9 без остатка.Решение:
Расчитаем количество частей: 8 + 6 + 9 = 23
Узнаем размер одной части: 564972 : 23 = 24564
8 * 24564 = 196512
6 * 24564 = 147384
9 * 24564 = 221076
Ответ: Результатом деления числа 564972 на три части в отношении 8:6:9 являются числа 196512 и 147384 и 221076.
Проверка: 196512 + 147384 + 221076 = 564972
Разделите число 564972 на 3 части в отношении 8:7:8 без остатка.Решение:
Расчитаем количество частей: 8 + 7 + 8 = 23
Узнаем размер одной части: 564972 : 23 = 24564
8 * 24564 = 196512
7 * 24564 = 171948
8 * 24564 = 196512
Ответ: Результатом деления числа 564972 на три части в отношении 8:7:8 являются числа 196512 и 171948 и 196512.
Проверка: 196512 + 171948 + 196512 = 564972
Разделите число 564972 на 3 части в отношении 8:8:7 без остатка.Решение:
Расчитаем количество частей: 8 + 8 + 7 = 23
Узнаем размер одной части: 564972 : 23 = 24564
8 * 24564 = 196512
8 * 24564 = 196512
7 * 24564 = 171948
Ответ: Результатом деления числа 564972 на три части в отношении 8:8:7 являются числа 196512 и 196512 и 171948.
Проверка: 196512 + 196512 + 171948 = 564972
Разделите число 564972 на 3 части в отношении 8:9:6 без остатка.Решение:
Расчитаем количество частей: 8 + 9 + 6 = 23
Узнаем размер одной части: 564972 : 23 = 24564
8 * 24564 = 196512
9 * 24564 = 221076
6 * 24564 = 147384
Ответ: Результатом деления числа 564972 на три части в отношении 8:9:6 являются числа 196512 и 221076 и 147384.
Проверка: 196512 + 221076 + 147384 = 564972
Разделите число 564972 на 3 части в отношении 9:1:2 без остатка.Решение:
Расчитаем количество частей: 9 + 1 + 2 = 12
Узнаем размер одной части: 564972 : 12 = 47081
9 * 47081 = 423729
1 * 47081 = 47081
2 * 47081 = 94162
Ответ: Результатом деления числа 564972 на три части в отношении 9:1:2 являются числа 423729 и 47081 и 94162.
Проверка: 423729 + 47081 + 94162 = 564972
Разделите число 564972 на 3 части в отношении 9:5:9 без остатка.Решение:
Расчитаем количество частей: 9 + 5 + 9 = 23
Узнаем размер одной части: 564972 : 23 = 24564
9 * 24564 = 221076
5 * 24564 = 122820
9 * 24564 = 221076
Ответ: Результатом деления числа 564972 на три части в отношении 9:5:9 являются числа 221076 и 122820 и 221076.
Проверка: 221076 + 122820 + 221076 = 564972
Разделите число 564972 на 3 части в отношении 9:6:8 без остатка.Решение:
Расчитаем количество частей: 9 + 6 + 8 = 23
Узнаем размер одной части: 564972 : 23 = 24564
9 * 24564 = 221076
6 * 24564 = 147384
8 * 24564 = 196512
Ответ: Результатом деления числа 564972 на три части в отношении 9:6:8 являются числа 221076 и 147384 и 196512.
Проверка: 221076 + 147384 + 196512 = 564972
Разделите число 564972 на 3 части в отношении 9:7:7 без остатка.Решение:
Расчитаем количество частей: 9 + 7 + 7 = 23
Узнаем размер одной части: 564972 : 23 = 24564
9 * 24564 = 221076
7 * 24564 = 171948
7 * 24564 = 171948
Ответ: Результатом деления числа 564972 на три части в отношении 9:7:7 являются числа 221076 и 171948 и 171948.
Проверка: 221076 + 171948 + 171948 = 564972
Разделите число 564972 на 3 части в отношении 9:8:6 без остатка.Решение:
Расчитаем количество частей: 9 + 8 + 6 = 23
Узнаем размер одной части: 564972 : 23 = 24564
9 * 24564 = 221076
8 * 24564 = 196512
6 * 24564 = 147384
Ответ: Результатом деления числа 564972 на три части в отношении 9:8:6 являются числа 221076 и 196512 и 147384.
Проверка: 221076 + 196512 + 147384 = 564972
Разделите число 564972 на 3 части в отношении 9:9:5 без остатка.Решение:
Расчитаем количество частей: 9 + 9 + 5 = 23
Узнаем размер одной части: 564972 : 23 = 24564
9 * 24564 = 221076
9 * 24564 = 221076
5 * 24564 = 122820
Ответ: Результатом деления числа 564972 на три части в отношении 9:9:5 являются числа 221076 и 221076 и 122820.
Проверка: 221076 + 221076 + 122820 = 564972
На рисунке изображен график функции вида
Дата: 2021-09-05
952
Категория: Графики функций
Метка: ЕГЭ-№10
564198. На рисунке изображен график функции вида
Найдите f(13).
График функции имеет горизонтальную асимптоту y=2, значит с=2. Вертикальная асимптота x=3, то есть b= -3. По графику дана точка f(2)=1, можем записать:Таким образом
Ответ: 2,1
Еще вариант решения: Вспомним, что гипербола y=a/x по сути идентична гиперболеНо! Что тут делают коэффициенты и как они «участвуют»? Как влияют на график?
Коэффициент а – влияет на «приближение-отдаление» ветвей гиперболы относительно осей. Попробуйте построить графики с разными коэффициентами, например 0,25; 0,5; 2; 4 и увидите, как это выглядит.
Коэффициент b – влияет на сдвиг графика вдоль оси ох (правее-левее). Если непосредственно перед коэффициентом стоит знак ПЛЮС формула, то гипербола смещена в отрицательном направлении оси; если МИНУС, то в положительном направлении.
Коэффициент с – влияет на сдвиг графика вдоль оси оу (вверх-вниз). Если перед коэффициентом стоит ПЛЮС, то график смещен в положительном направлении; если МИНУС, то в отрицательном.
*Например:График сдвинут вдоль оси оу на три единицы в положительном направлении, и вдоль оси ох на пять единиц в положительном направлении.
График сдвинут вдоль оси оу на четыре единицы в отрицательном направлении, и вдоль оси ох на десять единиц в отрицательном направлении.
Если вы имеете практику в работе графиком и пониманием того как он располагается в зависимости от коэффициентов, то вы легко эти коэффициенты определите.
В данной задаче видим, что центр симметрии гиперболы имеет координату (3;2), то есть он смещен по оси оу на две единицы в положительном направлении, значит с=2. По оси ох смещен в положительном направлении на три единицы, значит b=–3.
Коэффициент a=1. Это для опытных. Видно, что это каноническая гипербола у=1/х. Просто она смещена.
Записываем:Ответ: 2,1
*Конечно же, можно записать формулу в следующем виде (преобразовываем знаменатель):
Просто тогда будет так => с=2 и b=3. Суть не меняется.
На рисунке изображен график функции
Найдите при каком значении х значение функции равно 0,8.
Отметим, что гипербола сдвинута вдоль оси оу на единицу вверх (в положительном направлении). Центром симметрии графика является точка (0;1).
На графике обозначена точка (3;2), так как нам известен центр симметрии, то еще одну точку через которую проходит график установить не трудно (-3;0). Подставляем значения в функцию и находим коэффициенты:
Коэффициенты найдены. Вычисляем х при котором значение функции равно 0,8:
Ответ: -15
508971. На рисунке изображен график функции
Найдите f(19)
Отметим, что гипербола сдвинута вдоль оси ох на единицу влево (в отрицательном направлении). Центром симметрии графика является точка (-1;0).
На графике обозначена точка (2;1), используя центр симметрии установим еще одну (-4;-1). Подставляем значения в функцию и находим коэффициенты:
Ответ: 0,15
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
На чтение 5 мин. Просмотров 5 Опубликовано 11.03.2023
Содержание
- Задания 1-11 вариант 393 ларин егэ 07.05.2022 математика профиль
- Ларин александр
александрович. математика. репетитор.
- Решение вариантов алекса ларина егэ, огэ математика | виктор осипов
Задания 1-11 вариант 393 ларин егэ 07.05.2022 математика профиль
Разбор заданий 1-11 варианта ЕГЭ № 393 Александр Ларин. Математика, профильный уровень. Пользуемся таймингом по задачам ниже.
00:00
1) Решите уравнение log_(1945)(x 2)=log_(1945)(x^2—3x-10)
03:02
2) Грамоты призеров математического конкурса хранятся в трех коробках – по 400 грамот в первых двух, а остальные грамоты в третьей. Участник Б. приходит за своей грамотой. Найдите вероятность того, что его грамота найдется в третьей или второй коробках, если всего в конкурсе 1945 призеров. Ответ округлите до сотых.
05:05
3) В прямоугольном треугольнике PBD c прямым углом при вершине В сторона PD равна 1945, а котангенс угла Р равен 0,75. Найдите радиус окружности, вписанной в треугольник PBD.
13:09
4) Вычислите (-4tg137*tg47*sin1945)/(cos55)
17:20
5) Дана правильная треугольная призма со стороной основания sqrt(3) и высотой 1945/pi. Найдите объем цилиндра, описанного около этой призмы.
21:55
6) На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной в точке x0 .
23:17
7) Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t)=-5t^2 18t, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров?
26:56

33:15
9) На рисунке изображён график функции f(x)=log_(a)(x b). Найдите x, при котором f(x)=-5.
40:15
10) Найдите вероятность того, что в случайном семизначном телефонном номере последняя цифра не больше 3, а две цифры перед ней не больше 2.
43:52
11) Найдите точку максимума функции y=1945 ln(-x^2 18x 1945).
Решение задания № 12 варианта 393 Ларин здесь
https://rutube.ru/video/9b136a56b6a17ca5595f524cf6cae404/
Решение задания № 14 варианта 393 Ларин здесь
https://rutube.ru/video/137b18c47d9f6e5c2a866b175e4e9728/
Канал Яндекс.Дзен
https://zen.yandex.ru/matem
Ларин александр
александрович. математика. репетитор.
20.07.22
В разделе
ДВИ опубликован
вариант
5 потока ДВИ.
Обсуждение…
19.07.22
В разделе
ДВИ опубликован
вариант
4 потока ДВИ.
Обсуждение…
15.07.22
В разделе
ДВИ опубликован
вариант
3 потока ДВИ.
Обсуждение…
14.07.22
В разделе
ДВИ опубликован
вариант
2 потока ДВИ.
Обсуждение…
11.07.22
В разделе
ДВИ опубликован
вариант 1 потока ДВИ.
Обсуждение…
03.07.22
В разделе
ДВИ опубликовано
расписание ДВИ МГУ 2022 г.
28.05.22
Опубликовантренировочный вариант
№396Обсуждение…
27.05.22 Опубликованыответы
к тренировочному варианту №395
21.05.22
Опубликовантренировочный вариант
№395
Обсуждение…
20.05.22 Опубликованыответы
к тренировочному варианту №394
18.05.22
ОГЭ —
опубликован Тренировочный
вариант №326 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
325 и
325у.
14.05.22
Опубликовантренировочный вариант
№394Обсуждение…
13.05.22
В разделе
ЕГЭ опубликован
три варианта пробника профильного ЕГЭ.Обсуждение…
13.05.22 Опубликованыответы
к тренировочному варианту №393
11.05.22
ОГЭ —
опубликован Тренировочный
вариант №325 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
324 и
324у.
07.05.22
Опубликовантренировочный вариант
№393Обсуждение…
06.05.22 Опубликованыответы
к тренировочному варианту №392
05.05.22
В разделе
ЕГЭ опубликован
образец варианта пробника профильного ЕГЭ с ответами и
решениями части с развернутым ответом и критериями оценивания.
Обсуждение…
04.05.22
ОГЭ —
опубликован Тренировочный
вариант №324 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
323 и
323у.
30.04.22
Опубликовантренировочный вариант
№392
Обсуждение…
29.04.22 Опубликованыответы
к тренировочному варианту №391
28.04.22
В разделе
ЕГЭ опубликован
образец варианта московского пробника 23 апреля 2022 года.
Обсуждение…
27.04.22
ОГЭ —
опубликован Тренировочный
вариант №323 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
322 и
322у.
23.04.22
Опубликовантренировочный вариант
№391Обсуждение…
22.04.22 Опубликованыответы
к тренировочному варианту №390
20.04.22
ОГЭ —
опубликован Тренировочный
вариант №322 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
321 и
321у.
16.04.22
Опубликовантренировочный вариант
№390Обсуждение…
15.04.22 Опубликованыответы
к тренировочному варианту №389
13.04.22
ОГЭ —
опубликован Тренировочный
вариант №321 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
320 и
320у.
12.04.22
В разделе
ЕГЭ опубликован
вариант пробного ЕГЭ
с ответами.
Обсуждение…
09.04.22
Опубликовантренировочный вариант
№389Обсуждение…
08.04.22 Опубликованыответы
к тренировочному варианту №388
06.04.22
ОГЭ —
опубликован Тренировочный
вариант №320 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
319 и
319у.
02.04.22
Опубликовантренировочный вариант
№388Обсуждение…
01.04.22 Опубликованыответы
к тренировочному варианту №387
30.03.22
В разделе
ЕГЭ опубликован
вариант пробного ЕГЭ
с ответами.
Обсуждение…
30.03.22
ОГЭ —
опубликован Тренировочный
вариант №319 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
318 и
318у.
29.03.22
В разделе
ЕГЭ опубликованы
4 варианта пробного ЕГЭ (март, Башкирия).
Обсуждение…
Решение вариантов алекса ларина егэ, огэ математика | виктор осипов
Здесь представлены решения тренировочных вариантов Алекса Ларина (egelive.ru). Каждую неделю я разбираю новые варианты ЕГЭ и ОГЭ, решение которых вы найдете на этой странице. Тем, кому удобнее смотреть в видеоформате — подписывайтесь на мой ютуб-канал
9 марта 2023
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой

9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika
На чтение 1 мин Просмотров 7 Опубликовано 7 марта, 2023
Задания В2 ЕГЭ по математике 2014 (с сайта РЕШУ ЕГЭ) Решение и ответы на задачи на официальном сайте источника онлайн.
Задания В2 ЕГЭ по математике 2014 (с сайта РЕШУ ЕГЭ)
Варианты ответов и решение задачи — МАТЕРИАЛЫ ТУТ: https://nsportal.ru/shkola/algebra/library/2014/04/11/zadaniya-v2-ege-po-matematike-2014-s-sayta-reshu-ege
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.