Задания
Версия для печати и копирования в MS Word
Тип 10 № 564202
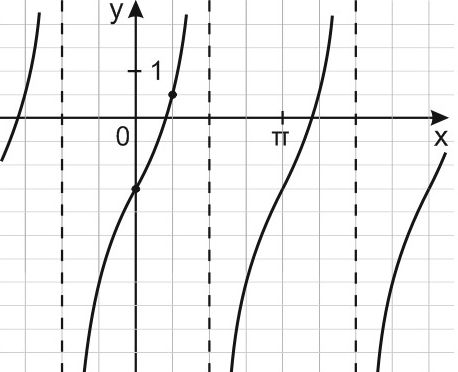
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Спрятать решение
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: 9,5.
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тема .
ЕГЭ Обществознание с HISTRUCTOR
.
02
21. Анализ экономического графика HIS
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
егэ обществознание с histructor
.0117-20. Задания по тексту HIS
.0221. Анализ экономического графика HIS
.0322. Задание – задача
.0423. Задание по Конституции
.0524. План HIS
.0625. Причинно-следственные связи и примеры социальных явлений
.07тест
Решаем задачу:
Задание 21. На графике изображено изменение ситуации на рынке ремонтно-строительных услуг в стране z. Предложение переместилось из положения s в положение s1 при неизменном спросе d. (на графике p – цена товара, q – количество товара.) (3 балла)
Как изменилась равновесная цена?
Что могло вызвать изменение предложения? Укажите любое одно обстоятельство (фактор) и объясните его влияние на предложение. (объяснение должно быть дано применительно к рынку, указанному в тексте задания.
Как изменятся спрос и равновесная цена на данном рынке, если при прочих равных условиях вырастут доходы потребителей̆?
Показать ответ и решение
1) равновесная цена увеличилась
2) стоимость ресурсов. Удорожание ресурсов для выполнения ремонтно-строительных услуг привело к сокращению предложения на данном рынке.
3) спрос увеличится, равновесная цена увеличится
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
На чтение 5 мин. Просмотров 6 Опубликовано 11.03.2023
Содержание
- Задания 1-11 вариант 393 ларин егэ 07.05.2022 математика профиль
- Ларин александр
александрович. математика. репетитор.
- Решение вариантов алекса ларина егэ, огэ математика | виктор осипов
Задания 1-11 вариант 393 ларин егэ 07.05.2022 математика профиль
Разбор заданий 1-11 варианта ЕГЭ № 393 Александр Ларин. Математика, профильный уровень. Пользуемся таймингом по задачам ниже.
00:00
1) Решите уравнение log_(1945)(x 2)=log_(1945)(x^2—3x-10)
03:02
2) Грамоты призеров математического конкурса хранятся в трех коробках – по 400 грамот в первых двух, а остальные грамоты в третьей. Участник Б. приходит за своей грамотой. Найдите вероятность того, что его грамота найдется в третьей или второй коробках, если всего в конкурсе 1945 призеров. Ответ округлите до сотых.
05:05
3) В прямоугольном треугольнике PBD c прямым углом при вершине В сторона PD равна 1945, а котангенс угла Р равен 0,75. Найдите радиус окружности, вписанной в треугольник PBD.
13:09
4) Вычислите (-4tg137*tg47*sin1945)/(cos55)
17:20
5) Дана правильная треугольная призма со стороной основания sqrt(3) и высотой 1945/pi. Найдите объем цилиндра, описанного около этой призмы.
21:55
6) На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной в точке x0 .
23:17
7) Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t)=-5t^2 18t, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров?
26:56

33:15
9) На рисунке изображён график функции f(x)=log_(a)(x b). Найдите x, при котором f(x)=-5.
40:15
10) Найдите вероятность того, что в случайном семизначном телефонном номере последняя цифра не больше 3, а две цифры перед ней не больше 2.
43:52
11) Найдите точку максимума функции y=1945 ln(-x^2 18x 1945).
Решение задания № 12 варианта 393 Ларин здесь
https://rutube.ru/video/9b136a56b6a17ca5595f524cf6cae404/
Решение задания № 14 варианта 393 Ларин здесь
https://rutube.ru/video/137b18c47d9f6e5c2a866b175e4e9728/
Канал Яндекс.Дзен
https://zen.yandex.ru/matem
Ларин александр
александрович. математика. репетитор.
20.07.22
В разделе
ДВИ опубликован
вариант
5 потока ДВИ.
Обсуждение…
19.07.22
В разделе
ДВИ опубликован
вариант
4 потока ДВИ.
Обсуждение…
15.07.22
В разделе
ДВИ опубликован
вариант
3 потока ДВИ.
Обсуждение…
14.07.22
В разделе
ДВИ опубликован
вариант
2 потока ДВИ.
Обсуждение…
11.07.22
В разделе
ДВИ опубликован
вариант 1 потока ДВИ.
Обсуждение…
03.07.22
В разделе
ДВИ опубликовано
расписание ДВИ МГУ 2022 г.
28.05.22
Опубликовантренировочный вариант
№396Обсуждение…
27.05.22 Опубликованыответы
к тренировочному варианту №395
21.05.22
Опубликовантренировочный вариант
№395
Обсуждение…
20.05.22 Опубликованыответы
к тренировочному варианту №394
18.05.22
ОГЭ —
опубликован Тренировочный
вариант №326 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
325 и
325у.
14.05.22
Опубликовантренировочный вариант
№394Обсуждение…
13.05.22
В разделе
ЕГЭ опубликован
три варианта пробника профильного ЕГЭ.Обсуждение…
13.05.22 Опубликованыответы
к тренировочному варианту №393
11.05.22
ОГЭ —
опубликован Тренировочный
вариант №325 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
324 и
324у.
07.05.22
Опубликовантренировочный вариант
№393Обсуждение…
06.05.22 Опубликованыответы
к тренировочному варианту №392
05.05.22
В разделе
ЕГЭ опубликован
образец варианта пробника профильного ЕГЭ с ответами и
решениями части с развернутым ответом и критериями оценивания.
Обсуждение…
04.05.22
ОГЭ —
опубликован Тренировочный
вариант №324 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
323 и
323у.
30.04.22
Опубликовантренировочный вариант
№392
Обсуждение…
29.04.22 Опубликованыответы
к тренировочному варианту №391
28.04.22
В разделе
ЕГЭ опубликован
образец варианта московского пробника 23 апреля 2022 года.
Обсуждение…
27.04.22
ОГЭ —
опубликован Тренировочный
вариант №323 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
322 и
322у.
23.04.22
Опубликовантренировочный вариант
№391Обсуждение…
22.04.22 Опубликованыответы
к тренировочному варианту №390
20.04.22
ОГЭ —
опубликован Тренировочный
вариант №322 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
321 и
321у.
16.04.22
Опубликовантренировочный вариант
№390Обсуждение…
15.04.22 Опубликованыответы
к тренировочному варианту №389
13.04.22
ОГЭ —
опубликован Тренировочный
вариант №321 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
320 и
320у.
12.04.22
В разделе
ЕГЭ опубликован
вариант пробного ЕГЭ
с ответами.
Обсуждение…
09.04.22
Опубликовантренировочный вариант
№389Обсуждение…
08.04.22 Опубликованыответы
к тренировочному варианту №388
06.04.22
ОГЭ —
опубликован Тренировочный
вариант №320 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
319 и
319у.
02.04.22
Опубликовантренировочный вариант
№388Обсуждение…
01.04.22 Опубликованыответы
к тренировочному варианту №387
30.03.22
В разделе
ЕГЭ опубликован
вариант пробного ЕГЭ
с ответами.
Обсуждение…
30.03.22
ОГЭ —
опубликован Тренировочный
вариант №319 (обычная версия). Обсуждение…
и
усложненная версия этого варианта.
Обсуждение…,
а также ответы к вариантам
318 и
318у.
29.03.22
В разделе
ЕГЭ опубликованы
4 варианта пробного ЕГЭ (март, Башкирия).
Обсуждение…
Решение вариантов алекса ларина егэ, огэ математика | виктор осипов
Здесь представлены решения тренировочных вариантов Алекса Ларина (egelive.ru). Каждую неделю я разбираю новые варианты ЕГЭ и ОГЭ, решение которых вы найдете на этой странице. Тем, кому удобнее смотреть в видеоформате — подписывайтесь на мой ютуб-канал
Решу егэ математика профиль задание 9 564202
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509149
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.
По графику, G(−2) = −1, G(−1) = −3, G(2) = 3. Тогда
Решая полученную систему, получаем: A = 1, B = 1, из G(2) = 3 получим C = −3. Теперь найдём абсциссу точки B:
Задание 9 № 509149
Найдите абсциссу точки B.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль задание 9 564202
Решу егэ математика профиль задание 9 564202
Решу егэ математика профиль задание 9 564202
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509167
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.
По графику, F(2) = 1, тогда Значит, гипербола имеет вид
Заметим, что A — тангенс угла наклона прямой по отношению к оси абсцисс, тогда По графику, G(2) = 1, тогда Значит, функция прямой имеет вид
Задание 9 № 509167
По графику, f 2 1, тогда Значит, гипербола имеет вид.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль задание 9 564202
Решу егэ математика профиль задание 9 564202
Решу егэ математика профиль задание 9 564202
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509009
На рисунке изображён график функции Найдите
По рисунку определяем, что Тогда
Значит, Найдём значение
Приведем решение Ирины Шраго.
По графику определим значение B:
Заметим, что и найдем точку, в которой значение функции равно −2. Это точка 2, следовательно, A = 2. Значит, Найдём значение
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль задание 9 564202
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 9 № 509167
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.
По графику, F(2) = 1, тогда Значит, гипербола имеет вид
Заметим, что A — тангенс угла наклона прямой по отношению к оси абсцисс, тогда По графику, G(2) = 1, тогда Значит, функция прямой имеет вид
Задание 9 № 509167
По графику, f 2 1, тогда Значит, гипербола имеет вид.
За пи сы вай тесь на бес плат ное за ня тие.
Dankonoy. com
29.02.2020 21:53:37
2020-02-29 21:53:37
Источники:
Https://dankonoy. com/ege/ege12/archives/4648
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика профиль задание 9 564202
Решу егэ математика профиль задание 9 564202
Решу егэ математика профиль задание 9 564202
—>
На рисунке изображён график функции Найдите
На рисунке изображён график функции Найдите, при каком значении X значение функции равно 0,8.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите A.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите C.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите A.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите A.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите A.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите C.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите C.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите B.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите B.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите B.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение X, при котором
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение X, при котором
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение X, при котором
—>
Найдите значение x, при котором.
Ege. sdamgia. ru
05.03.2019 5:19:30
2019-03-05 05:19:30
Источники:
Https://ege. sdamgia. ru/test? theme=125&ttest=true
Задание 9 ЕГЭ по математике. Графики функций » /> » /> .keyword { color: red; } Решу егэ математика профиль задание 9 564202
Задание 9 ЕГЭ по математике. Графики функций
Задание 9 ЕГЭ по математике. Графики функций
В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №9 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 9 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №9 ЕГЭ.
Да, теоретического материала здесь много. Но он необходим — и для решения задания 9 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 9 в формате ЕГЭ-2021
Линейная функция
1. На рисунке изображён график функции. Найдите значение, при котором
Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:
Вычтем из первого уравнения второе:
Уравнение прямой имеет вид:
Найдем, при каком значение функции равно -13,5.
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Запишем формулы функций.
Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция
Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции
Вычтем из первого уравнения второе.
Прямая задается формулой:
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).
Для прямой, расположенной выше, угловой коэффициент равен
Эта прямая проходит через точку (-2; 4), поэтому: эта прямая задается формулой
Для точки пересечения прямых:
Квадратичная функция. Необходимая теория
4. На рисунке изображен график функции Найдите b.
На рисунке — квадратичная парабола полученная из графика функции сдвигом на 1 вправо, то есть
5. На рисунке изображен график функции. Найдите с.
На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид.
6. На рисунке изображён график функции Найдите
График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:
Формула функции имеет вид:
7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.
Найдем a, b и c в формуле функции. График этой функции пересекает ось ординат в точке (0; -3), поэтому
График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:
Найдем абсциссу точки B. Для точек A и B:
(это абсцисса точки A) или (это абсцисса точки B).
Степенные функции. Необходимая теория
8. На рисунке изображены графики функций и, которые пересекаются в точках А и В. Найдите абсциссу точки В.
График функции проходит через точку (2; 1); значит,
График функции проходит через точки (2; 1) и (1; -4), — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда
Для точек A и B имеем:
Отсюда (абсцисса точки A) или (абсцисса точки B).
9. На рисунке изображён график функции. Найдите f (6,76).
Функция задана формулой:
Ее график проходит через точку (4; 5); значит,
10. На рисунке изображен график функции. Найдите.
График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда =5.
Показательная функция. Необходимая теория
11. На рисунке изображён график функции Найдите
График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:
Поделим второе уравнение на первое:
Подставим во второе уравнение:
12. На рисунке изображен график функции. Найдите
График функции проходит через точку Это значит, что
Формула функции имеет вид: .
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции Найдите
График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.
Вычтем из второго уравнения первое:
Или — не подходит, так как (как основание логарифма).
14. На рисунке изображен график функции.
График логарифмической функции на рисунке проходит через точки и. Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:
Тригонометрические функции. Необходимая теория
15. На рисунке изображён график функции Найдите
График функции сдвинут на 1,5 вверх; Значит, Амплитуда (наибольшее отклонение от среднего значения).
Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на.
16. На рисунке изображён график функции
На рисунке — график функции Так как
График функции проходит через точку A Подставим и координаты точки А в формулу функции.
Так как получим:
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения
Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то
Пользуясь периодичностью функции, период которой T = 4, получим:
Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 9 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.
Как формулируется задание 9 ЕГЭ по математике.
Ege-study. ru
02.11.2017 18:45:31
2017-11-02 18:45:31
Источники:
Https://ege-study. ru/ru/ege/podgotovka/matematika/zadanie-9-ege-po-matematike-grafiki-funkcij/
Целое положительное
число 564202
.
Это полупростое число.
19 — сумма цифр.
У числа 4 делителя: 1, 2, 282101, 564202.
Обратное число к 564202 – 0.0000017724148443288042.
Перевод числа в другие системы счисления:
двоичный вид: 10001001101111101010, троичный вид: 1001122221101, восьмеричный вид: 2115752, шестнадцатеричный вид: 89BEA.
Число байт 564202 представляет из себя 550 килобайтов 1002 байта .
Азбука Морзе для числа 564202: ….. -…. ….- ..— —— ..—
Число 564202 не является числом Фибоначчи.
Косинус: -0.9728, тангенс: 0.2381, синус: -0.2316.
Логарифм натуральный числа равен 13.2432.
Логарифм десятичный равен 5.7514.
Квадратный корень: 751.1338, а кубический корень: 82.6314.
Возведение числа 564202 в квадрат: 3.1832e+11.
Число 564202 в секундах это 6 дней 12 часов 43 минуты 22 секунды .
Нумерологическое цифра числа 564202 — 1.
Вариант МА2210301 и ответы
Скачать ответы и
решения для вариантов
1.
Каждый день во время конференции расходуется 60 пакетиковчая.
Конференция длится 9 дней. В пачке чая 50 пакетиков. Какого наименьшего
количества пачек чая хватит на все дни конференции?
2.
Установите соответствие между величинами и их
возможнымизначениями: к каждому элементу первого столбца подберите
соответствующий элемент из второго столбца.
3.
В таблице показано расписание пригородных электропоездовпо
направлению Москва Курская – Крутое – Петушки. Владислав пришёл на станцию
Москва Курская в 18:20 и хочет уехать в Петушки на электропоезде без пересадок.
Найдите номер ближайшего электропоезда, который ему подходит.
5. В коробке вперемешку лежат чайные пакетики с
чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 4
раза больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно
выбранный из этой коробки пакетик окажется пакетиком с чёрным чаем.
8.
Некоторые учащиеся 10-х классов школы ходили в апреле наспектакль
«Гроза». В мае некоторые десятиклассники пойдут на постановку по пьесе
«Бесприданница», причём среди них не будет тех, кто ходил в апреле на спектакль
«Гроза». Выберите утверждения, которые будут верны при указанных условиях
независимо от того, кто из десятиклассников пойдёт на постановку по пьесе
«Бесприданница».
●
1) Каждый учащийся 10-х классов, который не ходил на спектакль
«Гроза», пойдёт на постановку по пьесе «Бесприданница».
●
2) Нет ни одного десятиклассника, который ходил на спектакль
«Гроза» и пойдёт на постановку по пьесе «Бесприданница».
●
3) Среди учащихся 10-х классов этой школы, которые не пойдут на
постановку по пьесе «Бесприданница», есть хотя бы один, который ходил на
спектакль «Гроза».
●
4) Найдётся десятиклассник, который не ходил на спектакль «Гроза»
и не пойдёт на постановку по пьесе «Бесприданница».
9.
На фрагменте географической карты схематично изображеныграницы
деревни Покровское и очертания озёр (площадь одной клетки равна одному
гектару). Оцените приближённо площадь озера Малого. Ответ дайте в гектарах с
округлением до целого значения.
10.
Диагональ прямоугольного экрана ноутбука равна 40 см, аширина
экрана ― 32 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
11.
Пирамида Снофру имеет форму правильной четырёхугольнойпирамиды,
сторона основания которой равна 220 м, а высота — 104 м. Сторона основания
точной музейной копии этой пирамиды равна 55 см. Найдите высоту музейной копии.
Ответ дайте в сантиметрах.
12.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°
, угол ABC равен 106° . Найдите угол ACB . Ответ дайте в градусах.
13.
Даны два цилиндра. Радиус основания и высота первогоцилиндра
равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго
цилиндра больше объёма первого?
15. В школе мальчики составляют 55 % от числа всех
учащихся. Сколько в этой школе мальчиков, если их на 50 человек больше, чем
девочек?
19.
Цифры четырёхзначного числа, кратного 5, записали вобратном
порядке и получили второе четырёхзначное число. Затем из исходного числа вычли
второе и получили 3366. В ответе укажите какое-нибудь одно такое исходное
число.
20.
Имеется два сплава. Первый содержит 45 % никеля, второй —5 %
никеля. Из этих двух сплавов получили третий сплав, содержащий 15 % никеля.
Масса первого сплава равна 40 кг. На сколько килограммов масса первого сплава
была меньше массы второго?
21.
Прямоугольник разбит на четыре меньших прямоугольникадвумя
прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и
далее по часовой стрелке, равны 2, 3 и 18. Найдите периметр четвёртого
прямоугольника.
Вариант МА2210305 и ответы
Скачать ответы и
решения для вариантов
1. Для покраски 1 кв. м потолка требуется 230 г
краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок
краски нужно для покраски потолка площадью 44 кв. м?
3. В таблице представлены налоговые ставки на
автомобили в Москве с 1 января 2013 года. Какова налоговая ставка (в рублях за
1 л. с. в год) на автомобиль мощностью 115 л. с.?
5.
Помещение освещается двумя лампами. Вероятностьперегорания одной
лампы в течение года равна 0,3. Найдите вероятность того, что в течение года
обе лампы перегорят.
6.
В таблице даны результаты олимпиад по русскому языку ибиологии в
9 «А» классе. Похвальные грамоты дают тем школьникам, у кого суммарный балл по
двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60
баллов. Укажите номера учащихся 9 «А» класса, набравших меньше 60 баллов по
русскому языку и получивших похвальные грамоты, без пробелов, запятых и других
дополнительных символов.
7.
На рисунке изображены график функции и касательные,проведённые к
нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения
производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в
соответствие каждой точке значение производной функции в ней.
8.
Некоторые учащиеся 10-х классов школы ходили в ноябре наоперу
«Евгений Онегин». В марте некоторые десятиклассники пойдут на оперу «Руслан и
Людмила», причём среди них не будет тех, кто ходил в ноябре на оперу «Евгений
Онегин». Выберите утверждения, которые будут верны при указанных условиях независимо
от того, кто из десятиклассников пойдёт на оперу «Руслан и Людмила».
●
1) Каждый учащийся 10-х классов, который не ходил на оперу
«Евгений Онегин», пойдёт на оперу «Руслан и Людмила».
●
2) Нет ни одного десятиклассника, который ходил на оперу «Евгений
Онегин» и пойдёт на оперу «Руслан и Людмила».
●
3) Найдётся десятиклассник, который не ходил на оперу
«Евгений Онегин» и не пойдёт на оперу «Руслан и
Людмила».
●
4) Среди учащихся 10-х классов этой школы, которые не пойдут на
оперу «Руслан и Людмила», есть хотя бы один, который ходил на оперу «Евгений
Онегин».
9.
План местности разбит на клетки. Каждая клетка обозначаетквадрат
1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных
метрах.
10.
Пожарную лестницу длиной 10 м приставили к окну дома.Нижний конец
лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец
лестницы? Ответ дайте в метрах.
11.
Прямолинейный участок трубы длиной 4 м, имеющей всечении
окружность, необходимо покрасить снаружи (торцы трубы открыты, их красить не
нужно). Найдите площадь поверхности, которую необходимо покрасить, если внешний
обхват трубы равен 19 см. Ответ дайте в квадратных сантиметрах.
12.
В треугольнике ABC стороны AC и BC равны. Внешний угол при
вершине B равен 146° . Найдите угол C. Ответ дайте в градусах.
13.
Даны два шара радиусами 4 и 2. Во сколько раз объёмбольшего шара
больше объёма меньшего?
15. Число больных гриппом в школе уменьшилось за
месяц в пять раз. На сколько процентов уменьшилось число больных гриппом?
19.
Найдите пятизначное число, кратное 15, любые две соседниецифры
которого отличаются на 3. В ответе укажите какое-нибудь одно такое число.
20.
Теплоход, скорость которого в неподвижной воде равна 19 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт
теплоход возвращается через 43 часа после отправления из него. Сколько
километров проходит теплоход за весь рейс?
21.
На кольцевой дороге расположены четыре бензоколонки: А, Б,В и Г.
Расстояние между А и Б — 55 км, между А и В — 40 км, между В и Г — 40 км, между
Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей
дуге). Найдите расстояние (в километрах) между Б и В.
Вариант МА2210309 и ответы
Скачать ответы и
решения для вариантов
2.
Прямоугольный параллелепипед описан около цилиндра,радиус
основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту
цилиндра.
3.
В группе 16 человек, среди них — Анна и Татьяна. Группуслучайным
образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность
того, что Анна и Татьяна окажутся в одной подгруппе.
4.
Агрофирма закупает куриные яйца только в двух домашниххозяйствах.
Известно, что 40 % яиц из первого хозяйства — яйца высшей категории, а из
второго хозяйства — 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей
категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы,
окажется из первого хозяйства.
9. Пристани A и B расположены на озере, расстояние
между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На
следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч
больше прежней, сделав по пути остановку на 8 часов. В результате она затратила
на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость
баржи на пути из A в B. Ответ дайте в км/ч.
13. Основанием правильной пирамиды PABCD является
квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD
перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра
пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB
= 30.
15.
По вкладу «А» банк в конце каждого года планируетувеличивать на
13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать
эту сумму на 7 % в первый год и на целое число n процентов за второй год.
Найдите наименьшее значение n , при котором за два года хранения вклад «Б»
окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16.
В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M
. Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б)
Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22 .
18. У Ани есть 800 рублей. Ей нужно купить конверты
(большие и маленькие). Большой конверт стоит 32 рубля, а маленький — 25 рублей.
При этом число маленьких конвертов не должно отличаться от числа больших
конвертов больше чем на пять. а) Может ли Аня купить 24 конверта? б) Может ли
Аня купить 29 конвертов? в) Какое наибольшее число конвертов может купить Аня?
Вариант МА2210311 и ответы
Скачать ответы и
решения для вариантов
1.
Найдите периметр прямоугольника, если его площадь равна 12,а
отношение соседних сторон равно 1:3.
2.
Шар вписан в цилиндр. Площадь полной поверхностицилиндра равна
78. Найдите площадь поверхности шара.
3.
В магазине в среднем из 120 сумок 15 имеют скрытые
дефекты.Найдите вероятность того, что выбранная в магазине сумка окажется со
скрытыми дефектами.
4.
Игральный кубик бросают дважды. Известно, что в суммевыпало 11
очков. Найдите вероятность того, что во второй раз выпало 5 очков.
9. Игорь и Паша, работая вместе, могут покрасить
забор за 40 часов. Паша и Володя, работая вместе, могут покрасить этот же забор
за 48 часов, а Володя и Игорь, работая вместе, — за 60 часов. За сколько часов
мальчики покрасят забор, работая втроём?
13. Основанием правильной пирамиды PABCD является
квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD
перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра
пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если
AB = 24 .
15.
По вкладу «А» банк в конце каждого года планируетувеличивать на
11 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать
эту сумму на 7 % в первый год и на целое число n процентов за второй год.
Найдите наименьшее значение n , при котором за два года хранения вклад «Б»
окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16.
В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M
. Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б)
Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 18.
18. У Ани есть 400 рублей. Ей нужно купить конверты
(большие и маленькие). Большой конверт стоит 22 рубля, а маленький — 17 рублей.
При этом число маленьких конвертов не должно отличаться от числа больших
конвертов больше чем на пять. а) Может ли Аня купить 19 конвертов? б) Может ли
Аня купить 23 конверта? в) Какое наибольшее число конвертов может купить Аня?
Скачать ответы и
решения для вариантов