Задания
Версия для печати и копирования в MS Word
Тип 10 № 564210
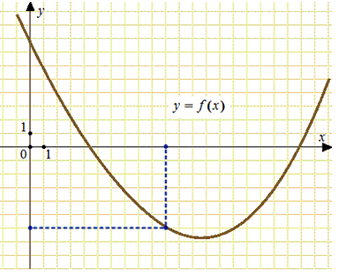
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Спрятать решение
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: −2,75.
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тема .
ЕГЭ Обществознание с HISTRUCTOR
.
02
21. Анализ экономического графика HIS
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
егэ обществознание с histructor
.0117-20. Задания по тексту HIS
.0221. Анализ экономического графика HIS
.0322. Задание – задача
.0423. Задание по Конституции
.0524. План HIS
.0625. Причинно-следственные связи и примеры социальных явлений
.07тест
Решаем задачу:
Задание 21. На графике изображено изменение ситуации на потребительском рынке легковых автомобилей в стране Z. Кривая предложения переместилась из положения S в положение S1 при неизменном спросе D. (На графике P — цена товара; Q — количество товара).
Как изменилась равновесная цена? Что могло вызвать изменение предложения?
Укажите любое одно обстоятельство (фактор) и объясните его влияние на предложение. (Объяснение должно быть дано применительно к рынку, указанному в тексте задания.)
Как изменятся спрос и равновесная цена на данном рынке, если вырастут доходы населения при прочих равных условиях? (3 БАЛЛА)
Показать ответ и решение
1) ответ на первый вопрос: равновесная цена уменьшилась;
2) Налоги. Понижение налоговой ставки на прибыль для производителей данной отрасли привело к увеличению производства, следовательно, и к увеличению предложения. Засчитывается только объяснение, данное применительно к рынку, указанному в тексте задания.
Ответ на второй вопрос засчитывается только при правильном указании обстоятельства/фактора и объяснения).
3) ответ на третий вопрос: рост доходов населения приведёт к увеличению спроса и увеличению равновесной цены.(Ответ на третий вопрос засчитывается только при правильном указании изменения спроса и равновесной цены.)
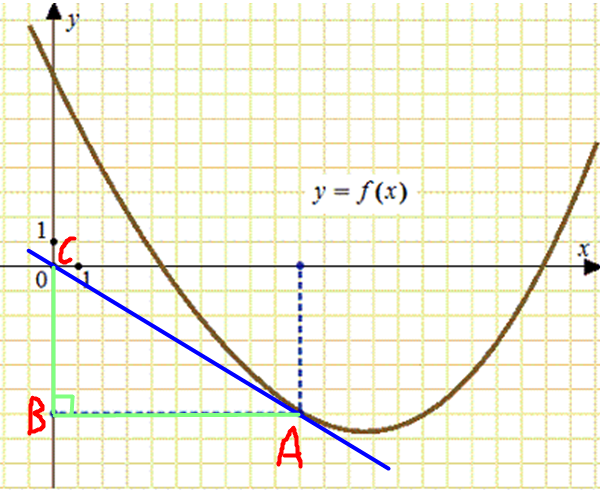
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 9
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим прямую, проходящую через начала координат (left( {0;,0} right)) и точку (left( {10;, — 6} right)), а также прямоугольный треугольник с вершинами в точках (Aleft( {10;, — 6} right),,,Bleft( {0;, — 6} right),,,Cleft( {0;,0} right)) (см. рисунок). Угол наклона касательной к оси абсцисс будет равен углу, смежному углу CAB. Поэтому:
(f’left( {{x_0}} right) = {rm{tg}}left( {{{180}^circ } — angle CAB} right) = — {rm{tg}}angle CAB = — frac{{CB}}{{AB}} = — frac{6}{{10}} = — 0,6.)
Ответ: –0,6.
математика росдистант
Был(а) на сайте 1 час назад
Раздел
Математические дисциплины
если нужно продлю, выполнит в бланке по 2 задание в каждом бланке кроме задание 3 там одно. вариант 9, ворд не рукописный
- Разместите заказ
- Выберите исполнителя
- Получите результат
| Гарантия на работу | 1 год |
| Средний балл | 4.96 |
| Стоимость | Назначаете сами |
| Эксперт | Выбираете сами |
| Уникальность работы | от 70% |
Нужна аналогичная работа?
Оформи быстрый заказ и узнай стоимость
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Неотрицательное
шестизначное
число 564210
– составное.
18 — сумма всех цифр.
Число имеет следующие делители: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90, 6269, 12538, 18807, 31345, 37614, 56421, 62690, 94035, 112842, 188070, 282105, 564210.
0.0000017723897130501054 является обратным числом к 564210.
Это число можно представить произведением простых чисел: 2 * 3 * 3 * 5 * 6269.
Представления числа:
двоичная система: 10001001101111110010, троичная: 1001122221200, восьмеричная: 2115762, шестнадцатеричная: 89BF2.
Число байт 564210 – это 550 килобайтов 1010 байтов .
Кодирование азбукой Морзе: ….. -…. ….- ..— .—- ——
Число — не число Фибоначчи.
Косинус числа: 0.3707, синус числа: -0.9288, тангенс числа: -2.5054.
Натуральный логарифм числа: 13.2432.
Десятичный логарифм равен 5.7514.
751.1391 — квадратный корень из числа 564210, 82.6317 — кубический.
Возведение числа в квадрат: 3.1833e+11.
Число 564210 в секундах это 6 дней 12 часов 43 минуты 30 секунд .
Цифра 9 — это нумерологическое значение числа 564210.
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Задачи из сборников Ященко, 2021 год
Квадратные уравнения
Показательные уравнения
Логарифмические уравнения
Модуль числа
Уравнения с модулем
Тригонометрический круг
Формулы тригонометрии
Формулы приведения
Простейшие тригонометрические уравнения 1
Простейшие тригонометрические уравнения 2
Тригонометрические уравнения
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
. От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
Давайте потренируемся.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Ответ:
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
От нее и отсчитываем.
Получим:
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
а)
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и
из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а)
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Сначала серия
Теперь серия
Ответ: .
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке
Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие
появляется, поскольку в уравнении есть
ОДЗ:
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси
.
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
и
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или
. Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие
. Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
На отрезке нам подходит корень
.
На отрезке нам подходят корни
.
На отрезке — корни
Ответ в пункте б):
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.