СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 10 № 564656
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите абсциссу вершины параболы.
Спрятать решение
Решение.
Из рисунка видно, что
следовательно,
Решая эту систему, находим
Абсцисса вершины параболы
Ответ: 4.
Аналоги к заданию № 564654: 564655 564656 564657 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №10. Парабола
Скачать файл в формате pdf.
ЕГЭ Профиль №10. Парабола
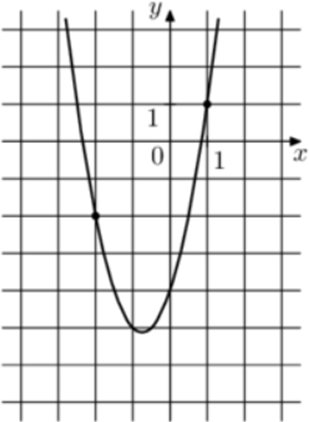
| Задача 1. На рисунке изображён график функции (fleft( x right) = 2{x^2} + b,x + c.) Найдите (fleft( { — 5} right).)
Ответ
ОТВЕТ: 31. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 2 + b + c,,,,}\{ — 2 = 8 — 2b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 6 + 3b,,,,,,, Leftrightarrow ,,,,,,,b = 3.) Тогда: (1 = 2 + 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 5} right) = 2 cdot {left( { — 5} right)^2} + 3 cdot left( { — 5} right) — 4 = 31.) Ответ: 31. |
|
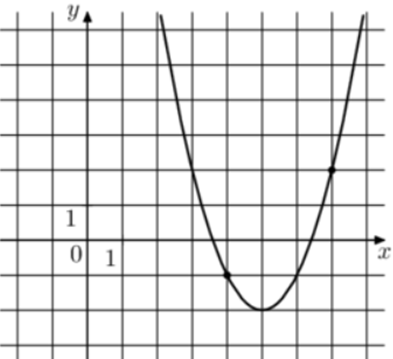
| Задача 2. На рисунке изображён график функции (fleft( x right) = {x^2} + b,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: 34. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {4; — 1} right)) и (left( {6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 16 + 4b + c,,,,}\{ — 1 = 36 + 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 20 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 10.) Тогда: ( — 1 = 16 — 40 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34. |
|
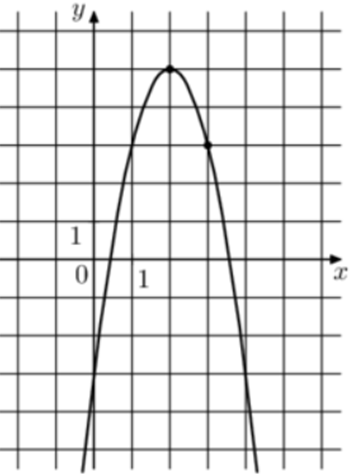
| Задача 3. На рисунке изображён график функции (fleft( x right) = — 2{x^2} + b,x + c.) Найдите (fleft( 6 right).)
Ответ
ОТВЕТ: — 27. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = — 2 + b + c,,,,,,,,}\{3 = — 18 + 3b + c,,,}end{array}} right.)Вычтем из первого уравнения второе: (0 = 16 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = 8.)Тогда: (3 = — 2 + 8 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 6 right) = — 2 cdot {6^2} + 8 cdot 6 — 3 = — 27.) Ответ: – 27. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 6 right) = — 2 cdot {left( {6 — 2} right)^2} + 5 = — 27.) Ответ: – 27. |
|
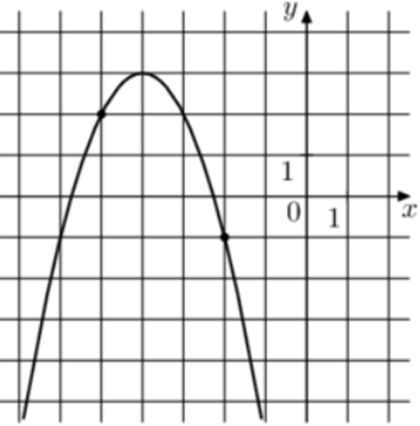
| Задача 4. На рисунке изображён график функции (fleft( x right) = — {x^2} + b,x + c.) Найдите (fleft( { — 8} right).)
Ответ
ОТВЕТ: — 13. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 3;2} right)) и (left( { — 5;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = — 9 — 3b + c,,,,,,,,}\{2 = — 25 — 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = 16 + 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 8.) Тогда: (2 = — 9 + 24 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 13.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} + 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13. |
|
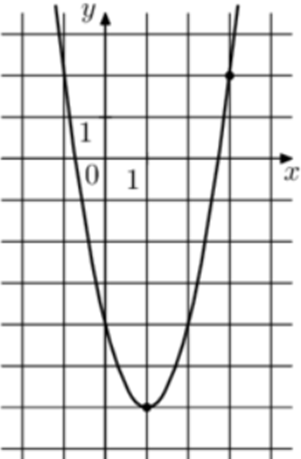
| Задача 5. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 4,x + c.) Найдите (fleft( { — 3} right).)
Ответ
ОТВЕТ: 26. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1; — 6} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 6 = a — 4 + c,,,,,,,,}\{2 = 9a — 12 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 8 = — 8a + 8,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 6 = 2 — 4 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 4x — 4) и (fleft( { — 3} right) = 2 cdot {left( { — 3} right)^2} — 4 cdot left( { — 3} right) — 4 = 26.) Ответ: 26. 2 Способ Заметим, что графиком является парабола (fleft( x right) = 2{x^2}), вершина которой находится в точке (left( {1; — 6} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = 2{left( {x — 1} right)^2} — 6) и (fleft( { — 3} right) = 2 cdot {left( { — 3 — 1} right)^2} — 6 = 26.) Ответ: 26. |
|
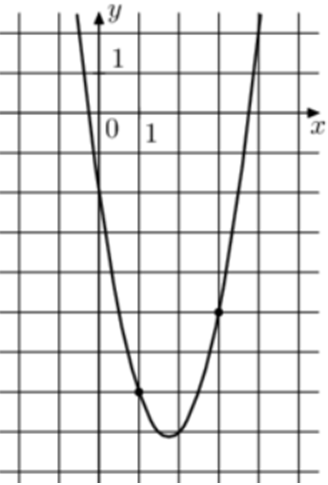
| Задача 6. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 7,x + c.) Найдите (fleft( 7 right).)
Ответ
ОТВЕТ: 47. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 7} right)) и (left( {3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 7 = a — 7 + c,,,,,,,,}\{ — 5 = 9a — 21 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 8a + 14,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 7 = 2 — 7 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 7x — 2) и (fleft( 7 right) = 2 cdot {7^2} — 7 cdot 7 — 2 = 47.) Ответ: 47. |
|
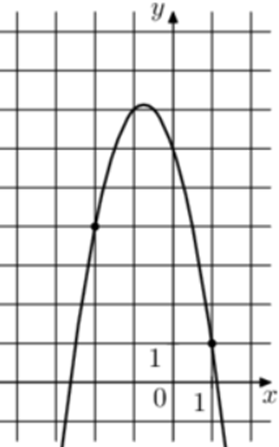
| Задача 7. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 3,x + c.) Найдите (fleft( { — 4} right).)
Ответ
ОТВЕТ: — 14. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a — 3 + c,,,,,,,,}\{4 = 4a + 6 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (1 = — 2 — 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 6.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 3x + 6) и (fleft( { — 4} right) = — 2 cdot {left( { — 4} right)^2} — 3 cdot left( { — 4} right) + 6 = — 14.) Ответ: – 14. |
|
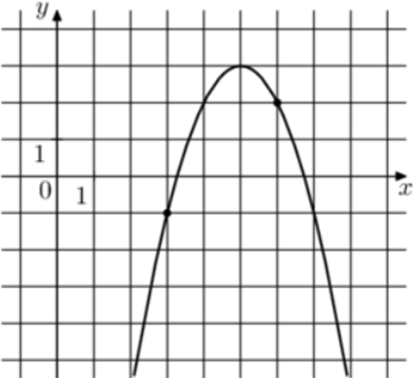
| Задача 8. На рисунке изображён график функции (fleft( x right) = a,{x^2} + 10,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: — 33. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {3; — 1} right)) и (left( {4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 9a + 30 + c}\{2 = 16a + 40 + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — 10,,,,,,, Leftrightarrow ,,,,,,,a = — 1.) Тогда: ( — 1 = — 9 + 30 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 22.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} + 10x — 22) и (fleft( { — 1} right) = — {left( { — 1} right)^2} + 10 cdot left( { — 1} right) — 22 = — 33.) Ответ: – 33. 2 способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( {5;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x — 5} right)^2} + 3) и (fleft( { — 1} right) = — {left( { — 1 — 5} right)^2} + 3 = — 33.) Ответ: – 33. |
|
| Задача 9. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 6.) Найдите (fleft( { — 6} right).)
Ответ
ОТВЕТ: 48. |
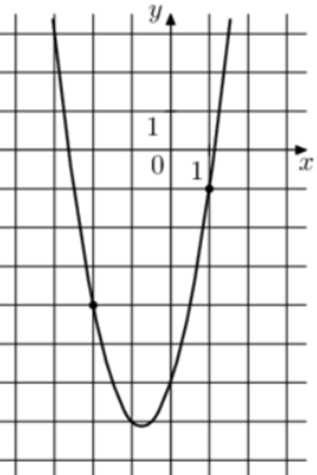 |
|
Решение
Парабола проходит через точки (left( {1; — 1} right)) и (left( { — 2; — 4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6,,,,,,,,,,,,,,,,,,,,,}\{ — 4 = 4a — 2b — 6left| {:left( { — 2} right)} right.,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6}\{2 = — 2a + b + 3}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 1 = 2 + b — 6,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 6) и (fleft( { — 6} right) = 2 cdot {left( { — 6} right)^2} + 3 cdot left( { — 6} right) — 6 = 48.) Ответ: 48. |
|
| Задача 10. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 4.) Найдите (fleft( { — 4} right).)
Ответ
ОТВЕТ: 16. |
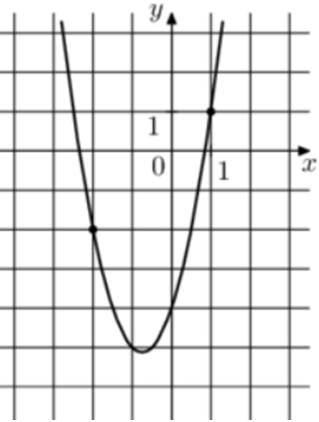 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,,,,,,,,,,,,,,,,,,,}\{-2 = 4a — 2b — 4left| {:left( { — 2} right)} right.,,,}end{array},,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,}\{1 = — 2a + b + 2}end{array}} right.} right.) Вычтем из первого уравнения второе: (0 = 3a — 6,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = 2 + b — 4,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 4} right) = 2 cdot {left( { — 4} right)^2} + 3 cdot left( { — 4} right) — 4 = 16.) Ответ: 16. |
|
| Задача 11. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + 2.) Найдите (fleft( { — 3} right).)
Ответ
ОТВЕТ: — 37. |
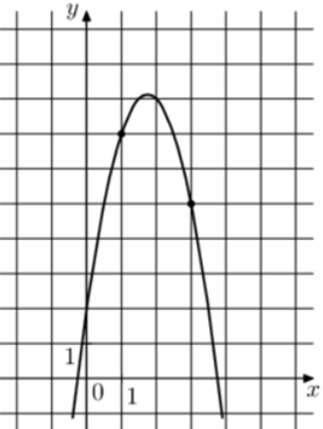 |
|
Решение
Парабола проходит через точки (left( {1;7} right)) и (left( {3;5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{7 = a + b + 2,,,,,,,,}\{5 = 9a + 3b + 2,,,,}end{array},,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b,,,,,,,,,,,,}\{3 = 9a + 3bleft| {:3} right.}end{array}} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b}\{1 = 3a + b}end{array}} right.,,,,,,,,,) Вычтем из первого уравнения второе: (4 = — 2a,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (5 = — 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 7x + 2) и (fleft( { — 3} right) = — 2 cdot {left( { — 3} right)^2} + 7 cdot left( { — 3} right) + 2 = — 37.) Ответ: – 37. |
|
| Задача 12. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 3.) Найдите (fleft( 8 right).)
Ответ
ОТВЕТ: — 67. |
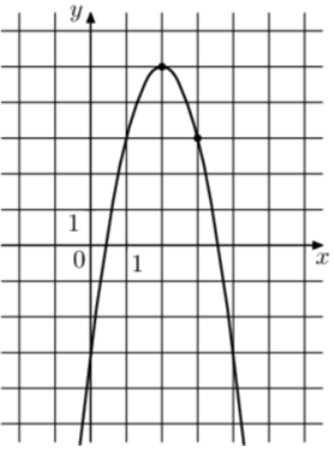 |
|
Решение
1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = a + b — 3,,,,,,,,,,,,,,,,,,}\{3 = 9a + 3b — 3left| {:3} right.,,,,,}end{array},,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{3 = a + b — 3}\{1 = 3a + b — 1}end{array}} right.} right.) Вычтем из первого уравнения второе: (2 = — 2a — 2,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (3 = — 2 + b — 3,,,,,,,, Leftrightarrow ,,,,,,,,b = 8.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 8 right) = — 2 cdot {8^2} + 8 cdot 8 — 3 = — 67.) Ответ: – 67. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 8 right) = — 2 cdot {left( {8 — 2} right)^2} + 5 = — 67.) Ответ: – 67. |
|
| Задача 13. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 7} right).)
Ответ
ОТВЕТ: 32. |
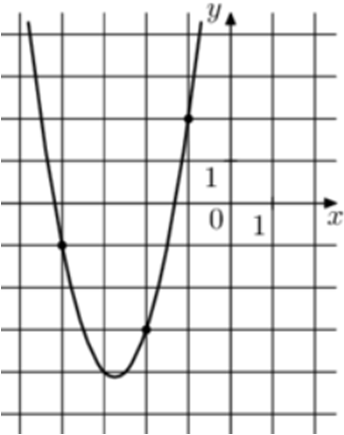 |
|
Решение
Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2; — 3} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,}\{ — 3 = 4a — 2b + c}\{ — 1 = 16a — 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (5 = — 3a + b.) Вычтем из первого уравнения третье: (3 = — 15a + 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,1 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{5 = — 3a + b}\{1 = — 5a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (5 = — 3 cdot 2 + b,,,,,, Leftrightarrow ,,,,,,b = 11) и (2 = 2 — 11 + c,,,,, Leftrightarrow ,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( { — 7} right) = 2 cdot {left( { — 7} right)^2} + 11 cdot left( { — 7} right) + 11 = 32.) Ответ: 32. |
|
| Задача 14. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( {10} right).)
Ответ
ОТВЕТ: 64. |
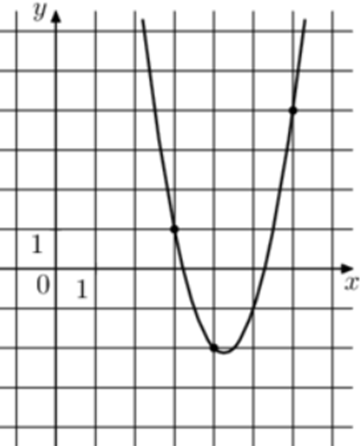 |
|
Решение
Парабола проходит через точки (left( {3;1} right)), (left( {4; — 2} right)) и (left( {6;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 9a + 3b + c,,,,,,,,,}\{ — 2 = 16a + 4b + c}\{4 = 36a + 6b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 7a — b) Вычтем из первого уравнения третье: ( — 3 = — 27a — 3bleft| {:left( { — 3} right),,,,,,,,, Leftrightarrow ,,,,,,,,,1 = 9a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{3 = — 7a — b}\{1 = 9a + b}end{array}} right.) Прибавим к первому уравнению второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (3 = — 7 cdot 2 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 17) и (1 = 9 cdot 2 + 3 cdot left( { — 17} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = 34.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 17x + 34) и (fleft( {10} right) = 2 cdot {10^2} — 17 cdot 10 + 34 = 64.) Ответ: 64. |
|
| Задача 15. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( 2 right).)
Ответ
ОТВЕТ: — 33. |
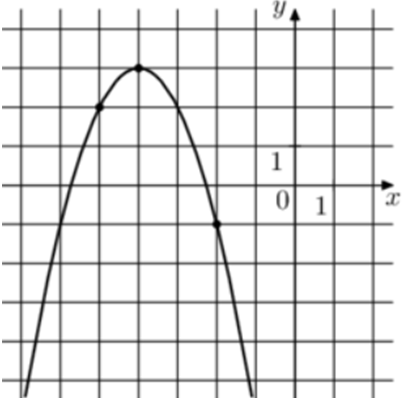 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 5;2} right)) и (left( { — 6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 25a — 5b + c,,,,,,,}\{ — 1 = 36a — 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 21a + 3bleft| {:3,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 7a + b} right..) Вычтем из первого уравнения третье: (0 = — 32a + 4bleft| {:4,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = — 8a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 7a + b}\{0 = — 8a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 1 = — 7 cdot left( { — 1} right) + b,,,,,, Leftrightarrow ,,,,,,b = — Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( 2 right) = -{2^2} — 8 cdot 2 — 13 = — 33.) Ответ: – 33. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}) вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( 2 right) = — {left( {2 + 4} right)^2} + 3 = — 33.) Ответ: – 33. |
|
| Задача 16. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: — 50. |
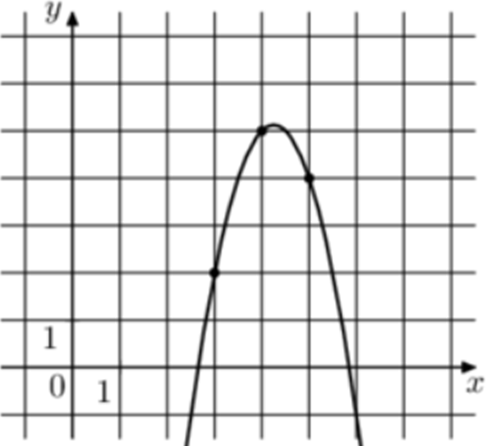 |
|
Решение
Парабола проходит через точки (left( {3;2} right)), (left( {4;5} right)) и (left( {5;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{5 = 16a + 4b + c,,,,,,}\{4 = 25a + 5b + c,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — b.) Вычтем из первого уравнения третье: ( — 2 = — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 7a — b}\{ — 1 = — 8a — b}end{array}} right.) Прибавим к первому уравнению второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 7 cdot left( { — 2} right) — b,,,,,,, Leftrightarrow ,,,,,,,b = 17) и (2 = 9 cdot left( { — 2} right) + 3 cdot 17 + c,,,,,, Leftrightarrow ,,,,,,c = — 31.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 17x — 31) и (fleft( { — 1} right) = — 2 cdot {left( { — 1} right)^2} + 17 cdot left( { — 1} right) — 31 = — 50.) Ответ: – 50. |
| Задача 17. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( 2 right).)
Ответ
ОТВЕТ: 41. |
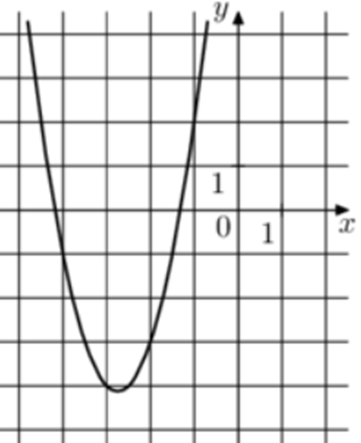 |
|
Решение
Парабола проходит через точки (left( { — 2; — 3} right)), (left( { — 3; — 4} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 3 = 4a — 2b + c,,,,,,,,,}\{ — 4 = 9a — 3b + c,,,,,,,,}\{ — 1 = 16a — 4b + c,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{1 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Прибавим к первому уравнению второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (1 = — 5 cdot 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 11) и ( — 3 = 4 cdot 2 — 2 cdot 11 + c,,,,,,, Leftrightarrow ,,,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( 2 right) = 2 cdot {2^2} + 11 cdot 2 + 11 = 41.) Ответ: 41. |
|
| Задача 18. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: 34. |
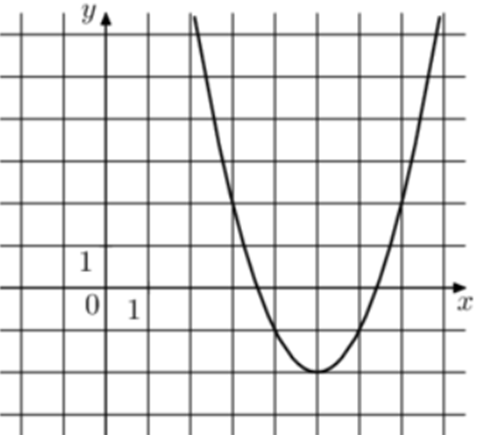 |
|
Решение
1 Способ Парабола проходит через точки (left( {3;2} right)), (left( {4; — 1} right)) и (left( {5; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{ — 1 = 16a + 4b + c,,,,,,,}\{ — 2 = 25a + 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (3 = -7a — b.) Вычтем из первого уравнения третье: (4 = — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,,,2 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{3 = — 7a — b}\{2 = — 8a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (3 = — 7 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 10) и (2 = 9 cdot 1 + 3 cdot left( { — 10} right) + c,,,,,, Leftrightarrow ,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34. |
|
| Задача 19. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 8} right).)
Ответ
ОТВЕТ: — 13. |
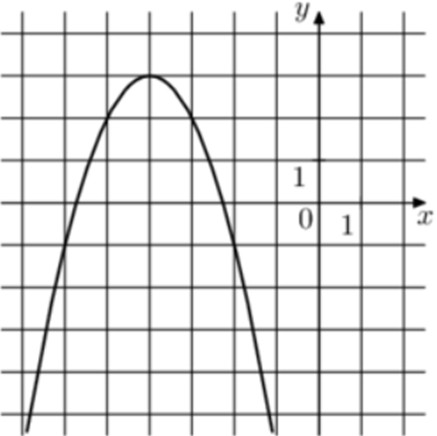 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 3;2} right)) и (left( { — 4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 9a — 3b + c,,,,,,,}\{3 = 16a — 4b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 4 = — 12a + 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 2 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 5a + b}\{ — 2 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 3 = — 5 cdot left( { — 1} right) + b,,,,,,, Leftrightarrow ,,,,,,,b = — Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} — 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13. |
|
| Задача 20. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 6} right).)
Ответ
ОТВЕТ: — 10. |
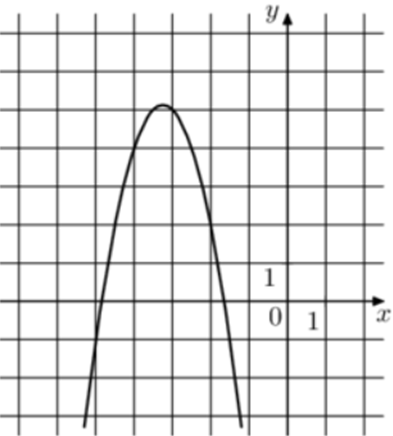 |
|
Решение
Парабола проходит через точки (left( { — 2;2} right)), (left( { — 3;5} right)) и (left( { — 4;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 4a — 2b + c,,,,,,,,,}\{5 = 9a — 3b + c,,,,,,,,}\{4 = 16a — 4b + c,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 5 cdot left( { — 2} right) + b,,,,,,, Leftrightarrow ,,,,,,b = — 13) и (2 = 4 cdot left( { — 2} right) — 2 cdot left( { — 13} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = — 16.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 13x — 16) и (fleft( { — 6} right) = — 2 cdot {left( { — 6} right)^2} — 13 cdot left( { — 6} right) — 16 = — 10.) Ответ: – 10. |
|
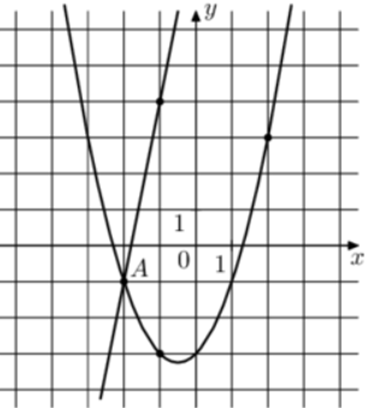
| Задача 21. На рисунке изображены графики функций (fleft( x right) = 5x + 9) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 6. |
 |
|
Решение
Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 1; — 3} right)) и (left( {1; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{ — 3 = a — b + c,,,,,,,,,,,,,,,}\{ — 1 = a + b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 3a — b.) Вычтем из первого уравнения третье: (0 = 3a — 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{2 = 3a — b}\{0 = a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 2a,,,,, Leftrightarrow ,,,,a = 1.) Тогда: (0 = 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 1) и ( — 1 = 4 cdot 1 — 2 cdot 1 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} + x — 3.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x + 9) и параболы (gleft( x right) = {x^2} + x — 3) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} + x — 3}\{y = 5x + 9,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,{x^2} + x — 3 = 5x + 9,,,,,, Leftrightarrow ,,,,,,{x^2} — 4x — 12 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 2,,,,{x_2} = 4.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна 4. Ответ: 4. |
|
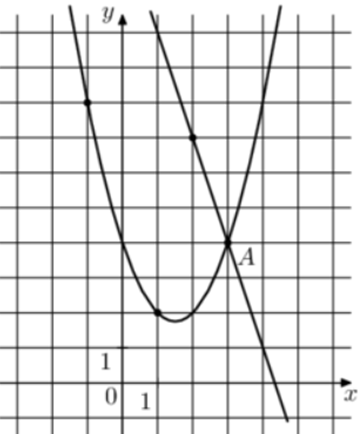
| Задача 22. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 3. |
 |
|
Решение
Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,{x^2} — 3x + 4 = — 3x + 13,,,,,,, Leftrightarrow ,,,,,,,{x^2} = 9,,,,,,, Leftrightarrow ,,,,,{x_1} = 3,,,,{x_2} = — 3.) Значение (x = 3) является абсциссой точки А. Следовательно, абсцисса точки В равна – 3. Ответ: – 3. |
|
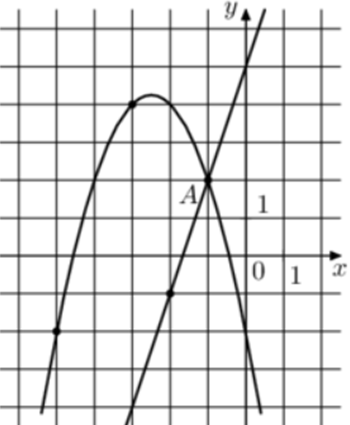
| Задача 23. На рисунке изображены графики функций (fleft( x right) = 3x + 5) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 7. |
 |
|
Решение
Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2;4} right)) и (left( { — 4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = 4a — 2b + c,,,,,,,,,,,,,,,}\{2 = 16a — 4b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 3a + b.) Вычтем из первого уравнения третье: (0 = — 15a + 3bleft| {:3,,,,,,,, Leftrightarrow ,,,,,,,0 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 2 = — 3a + b}\{0 = — 5a + b,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 2 = — 3 cdot left( { — 1} right) + b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и (2 = — 1 + 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} — 5x — 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 3x + 5) и параболы (gleft( x right) = — {x^2} — 5x — 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} — 5x — 2}\{y = 3x + 5,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,, — {x^2} — 5x — 2 = 3x + 5,,,,,, Leftrightarrow ,,,,,{x^2} + 8x + 7 = 0,,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = — 7.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 7. Ответ: – 7. |
|
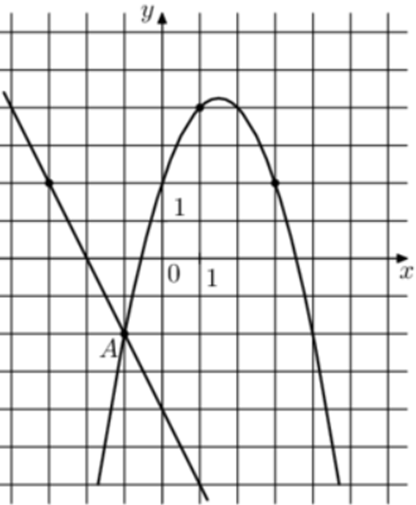
| Задача 24. На рисунке изображены графики функций (fleft( x right) = — 2x — 4) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 6. |
 |
|
Решение
Парабола проходит через точки (left( { — 1; — 2} right)), (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = — 2b,,,,,,, Leftrightarrow ,,,,,,b = 3.) Вычтем из первого уравнения третье: ( — 4 = — 8a — 4bleft| {:left( { — 2} right),,,,,,,,, Leftrightarrow ,,,,,,,,2 = 4a + 2b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{b = 3,,,,,,,,,,,,,,,,}\{2 = 4a + 2b,,,}end{array},,,,, Leftrightarrow ,,,,,,2 = 4a + 2 cdot 3,,,,,,,, Leftrightarrow ,,,,,,,,,a = — 1} right..) Тогда: ( — 2 = — 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,,c = 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} + 3x + 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 2x — 4) и параболы (gleft( x right) = — {x^2} + 3x + 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} + 3x + 2}\{y = — 2x — 4,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — ,{x^2} + 3x + 2 = — 2x — 4,,,,,, Leftrightarrow ,,,,,{x^2} — 5x — 6 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 6. Ответ: 6. |
|
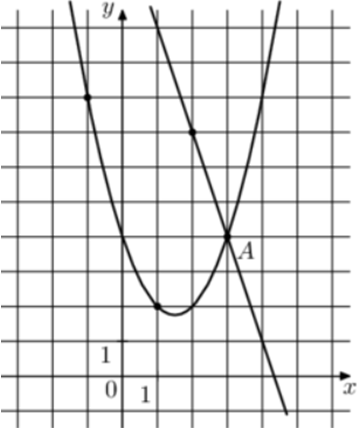
| Задача 25. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 22. |
 |
|
Решение
Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,}end{array}} right.,,, Leftrightarrow ,,,{x^2} — 3x + 4 = 13 — 3x,,, Leftrightarrow ,,,{x^2} = 9,,,, Leftrightarrow ,,,{x_1} = 3,,,,{x_2} = — 3,,, Leftrightarrow ,,,{y_1} = 4,,,{y_2} = 22.) Следовательно, (Aleft( {3;4} right)) и (Bleft( { — 3;22} right)). Таким образом, ордината точки В равна 22. Ответ: 22. |
|
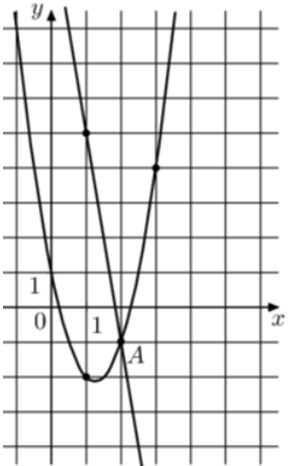
| Задача 26. На рисунке изображены графики функций (fleft( x right) = — 6x + 11) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 26. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 2} right)), (left( {2; — 1} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 2 = a + b + c}\{ — 1 = 4a + 2b + c}\{4 = 9a + 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: ( — 6 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 3 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{ — 3 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: ( — 1 = — 3 cdot 2 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и ( — 2 = 2 — 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = 2{x^2} — 5x + 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 6x + 11) и параболы (gleft( x right) = 2{x^2} — 5x + 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 2{x^2} — 5x + 1}\{y = — 6x + 11,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,2{x^2} — 5x + 1 = — 6x + 11,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + x — 10 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = — frac{5}{2},,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = — 1,,,,,{y_2} = 26.) Следовательно, (Aleft( {2; — 1} right)) и (Bleft( { — frac{5}{2};26} right)). Таким образом, ордината точки В равна 26. Ответ: 26. |
|
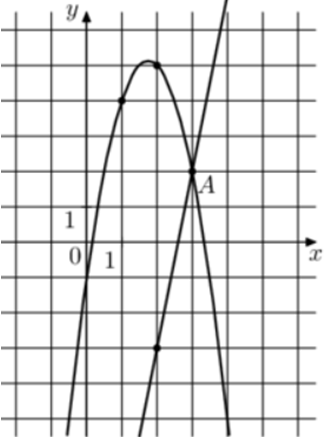
| Задача 27. На рисунке изображены графики функций (fleft( x right) = 5x — 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 23. |
 |
|
Решение
Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft| {:2,,,,,,, Leftrightarrow ,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x — 13) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = 5x — 13,,,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = 5x — 13,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 2x — 12 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 3,,,,,,{x_2} = — 2,,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 2,,,,,{y_2} = — 23.) Следовательно, (Aleft( {3;2} right)) и (Bleft( { — 2; — 23} right)). Таким образом, ордината точки В равна – 23. Ответ: – 23. |
|
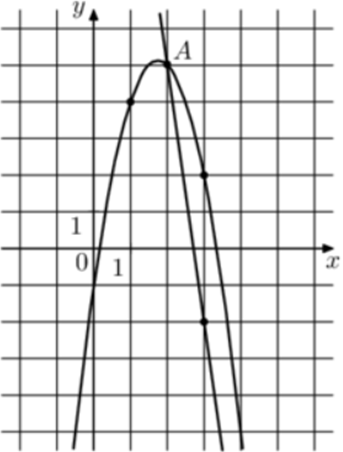
| Задача 28. На рисунке изображены графики функций (fleft( x right) = — 7x + 19) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 16. |
 |
|
Решение
Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 7x + 19) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = — 7x + 19,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = — 7x + 19,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 14x + 20 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = 5,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 5,,,,,{y_2} = — 16.) Следовательно, (Aleft( {2;5} right)) и (Bleft( {5; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16. |
|
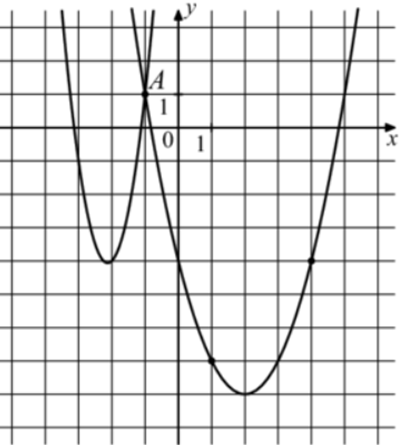
| Задача 29. На рисунке изображены графики функций (fleft( x right) = 4{x^2} + 17x + 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6. |
 |
|
Решение
График функции (fleft( x right) = 4{x^2} + 17x + 14) пересекает ось ординат в точке (left( {0;14} right)). Значит, график (y = fleft( x right)) изображён слева, а график (gleft( x right) = a{x^2} + bx + c) справа. Заметим, что графиком функции (y = gleft( x right)) является парабола (gleft( x right) = {x^2}), вершина которой находится в точке (left( {2; — 8} right)). Следовательно, ее уравнение будет иметь вид: (gleft( x right) = {left( {x — 2} right)^2} — 8 = {x^2} — 4x — 4.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} + 17x + 14}\{y = {x^2} — 4x — 4,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,4{x^2} + 17x + 14 = {x^2} — 4x — 4,,,,,,, Leftrightarrow ,,,,,,,3{x^2} + 21x + 18 = 0left| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} + 7x + 6 = 0,,,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = — 1,,,,{x_2} = — 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6. |
|
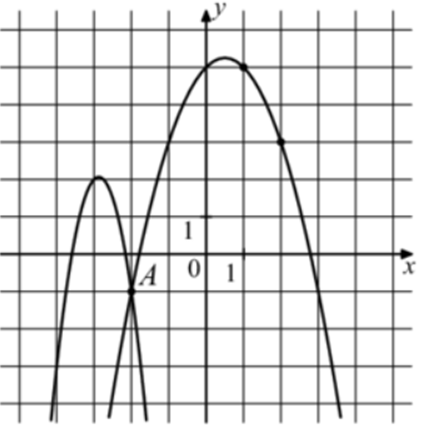
| Задача 30. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} — 23x — 31) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6. |
 |
|
Решение
График функции (fleft( x right) = — 4{x^2} — 23x — 31) пересекает ось ординат в точке (left( {0; — 31} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( { — 2; — 1} right)), (left( {1;5} right)) и (left( {2;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c}\{5 = a + b + c,,,,,,}\{3 = 4a + 2b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = 3a — 3b.) Вычтем из первого уравнения третье: ( — 4 = — 4b,,,,,, Leftrightarrow ,,,,,b = 1.) Тогда: ( — 6 = 3a — 3,,,,,, Leftrightarrow ,,,,,,a = — 1) и ( — 1 = — 4 — 2 + c,,,,,, Leftrightarrow ,,,,,,,c = 5.) Следовательно: (gleft( x right) = — {x^2} + x + 5.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 4{x^2} — 23x — 31}\{y = — {x^2} + x + 5,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — 4{x^2} — 23x — 31 = — {x^2} + x + 5,,,,, Leftrightarrow ,,,,,3{x^2} + 24x + 36 = 0left| {:3,,,, Leftrightarrow ,} right.) ( Leftrightarrow ,,,,,,{x^2} + 8x + 12 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} = — 2,,,,,,{x_2} = — 6.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6. |
|
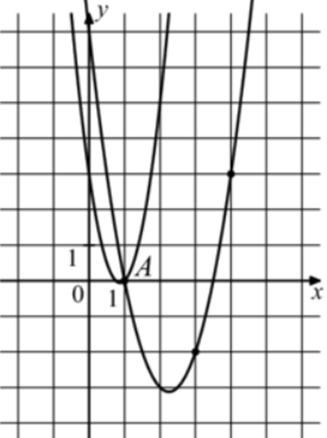
| Задача 31. На рисунке изображены графики функций (fleft( x right) = 4{x^2} — 7x + 3) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 33. |
 |
|
Решение
График функции (fleft( x right) = 4{x^2} — 7x + 3) пересекает ось ординат в точке (left( {0;3} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( {1;0} right)), (left( {3; — 2} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{0 = a + b + c,,,,,,,,}\{ — 2 = 9a + 3b + c}\{3 = 16a + 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 8a — 2bleft| {: 2,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b.} right.) Вычтем из первого уравнения третье: ( — 3 = — 15a — 3bleft| {:3} right.,,,,,, Leftrightarrow ,,,,, — 1 = — 5a — b.) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{1 = — 4a — b}\{ — 1 = — 5a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = — 4 cdot 2 — b,,,,,, Leftrightarrow ,,,,,,b = — 9) и (0 = 2 — 9 + c,,,,,,, Leftrightarrow ,,,,,,,c = 7.) Следовательно: (gleft( x right) = 2{x^2} — 9x + 7.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} — 7x + 3}\{y = 2{x^2} — 9x + 7}end{array},,,,,,, Leftrightarrow ,,,,,,4{x^2} — 7x + 3 = 2{x^2} — 9x + 7,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + 2x — 4 = 0left| {:2,,,,, Leftrightarrow } right.} right.) ( Leftrightarrow ,,,,,,,{x^2} + x — 2 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 2,,,,,,,,,,,,,,{y_1} = 0,,,,{y_2} = 33.) Следовательно, (Aleft( {1;0} right)) и (Bleft( { — 2;33} right)). Таким образом, ордината точки В равна 33. Ответ: 33. |
|
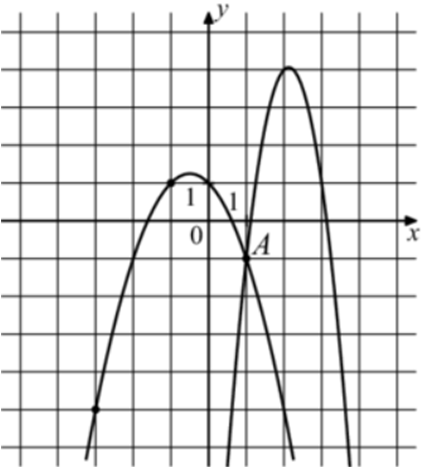
| Задача 32. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} + 17x — 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 29. |
 |
|
Решение
График функции (fleft( x right) = — 4{x^2} + 17x — 14) пересекает ось ординат в точке (left( {0; — 14} right)). Значит график функции (y = fleft( x right)) изображен справа, а график (gleft( x right) = a{x^2} + bx + c) слева, который проходит через точки (left( {1; — 1} right)), (left( { — 1;1} right)) и (left( { — 3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = a + b + c,,,,,,}\{1 = a — b + c,,,,,,,,}\{ — 5 = 9a — 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 1.) Вычтем из первого уравнения третье: (4 = — 8a + 4b,,,,, Leftrightarrow ,,,,,4 = — 8a — 4,,,,,, Leftrightarrow ,,,,,,a = — 1.) Тогда: ( — 1 = — 1 — 1 + c,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно: (gleft( x right) = — {x^2} — x + 1.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 4{x^2} + 17x — 14}\{y = — {x^2} — x + 1,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,, — 4{x^2} + 17x — 14 = — {x^2} — x + 1,,,,,, Leftrightarrow ,,,,,3{x^2} — 18x + 15 = 0left| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} — 6x + 5 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 5,,,,,,,,,{y_1} = — 1,,,,{y_2} = — 29.) Следовательно, (Aleft( {1; — 1} right)) и (Bleft( {5; — 29} right)). Таким образом, ордината точки В равна – 29. Ответ: – 29. |
Тема .
ЕГЭ Обществознание с HISTRUCTOR
.
02
21. Анализ экономического графика HIS
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
егэ обществознание с histructor
.0117-20. Задания по тексту HIS
.0221. Анализ экономического графика HIS
.0322. Задание – задача
.0423. Задание по Конституции
.0524. План HIS
.0625. Причинно-следственные связи и примеры социальных явлений
.07тест
Решаем задачу:
Задание 21. На графике изображено изменение ситуации на рынке ремонтно-строительных услуг в стране z. Предложение переместилось из положения s в положение s1 при неизменном спросе d. (на графике p – цена товара, q – количество товара.) (3 балла)
Как изменилась равновесная цена?
Что могло вызвать изменение предложения? Укажите любое одно обстоятельство (фактор) и объясните его влияние на предложение. (объяснение должно быть дано применительно к рынку, указанному в тексте задания.
Как изменятся спрос и равновесная цена на данном рынке, если при прочих равных условиях вырастут доходы потребителей̆?
Показать ответ и решение
1) равновесная цена увеличилась
2) стоимость ресурсов. Удорожание ресурсов для выполнения ремонтно-строительных услуг привело к сокращению предложения на данном рынке.
3) спрос увеличится, равновесная цена увеличится
338584 решу огэ математика
Задание 21 № 338584
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 40 минут раньше, чем велосипедист приехал в А, а встретились они через 15 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
Пусть — скорость мотоциклиста, — скорость велосипедиста. Примем расстояние между городами за единицу. Мотоциклист и велосипедист встретились через 15 минут, то есть через часа, после выезда, поэтому Мотоциклист прибыл в B на 40 минут, то есть на ч., раньше, чем велосипедист в А, откуда Получаем систему уравнений:
Скорость мотоциклиста не может быть отрицательной, поэтому скорость велосипедиста равна 1, а время, затраченное на весь путь равно одному часу.
Заметим, что в приведенном решении скорости выражаются не в км/час, а в условных единицах, и зависят от того, за какую величину принято расстояние между городами. Если бы расстояние между городами было принято за 10, то получилось бы V2=10 и V1=30. Однако найденное время не зависит от того, за какую величину принято расстояние между городами.
Приведем другое решение.
Пусть T — время, которое затратил на дорогу мотоциклист. Тогда время, затраченное велосипедистом, равно Пусть S — расстояние между городами, тогда скорость мотоциклиста равна а скорость велосипедиста равна Мотоциклист и велосипедист встретились через 15 минут, то есть через часа, после выезда, поэтому Умножив обе части уравнения на 4 и разделив на S, получим:
Время не может быть отрицательным, следовательно, мотоциклист затратил на дорогу часа, а велосипедист час.
Задание 21 № 338584
, раньше, чем велосипедист в А, откуда Получаем систему уравнений.
Oge. sdamgia. ru
22.01.2019 9:01:54
2019-01-22 09:01:54
Источники:
Https://oge. sdamgia. ru/test? pid=338584
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 338584 решу огэ математика
338584 решу огэ математика
338584 решу огэ математика
Задание 21 № 352780
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 33 минуты раньше, чем велосипедист приехал в А, а встретились они через 22 минуты после выезда. Сколько часов затратил на путь из В в А велосипедист?
Пусть — скорость мотоциклиста, — скорость велосипедиста. Примем расстояние между городами за единицу. Мотоциклист и велосипедист встретились через 22 минуты, то есть через часа, после выезда, поэтому Мотоциклист прибыл в B на 33 минуты раньше, чем велосипедист в А, откуда Получаем систему уравнений:
Скорость мотоциклиста не может быть отрицательной, поэтому скорость велосипедиста равна, а время, затраченное на весь путь равно
Задание 21 № 352780
Мотоциклист и велосипедист встретились через 22 минуты, то есть через часа, после выезда, поэтому Мотоциклист прибыл в B на 33 минуты раньше, чем велосипедист в А, откуда Получаем систему уравнений.
Math-oge. sdamgia. ru
07.08.2020 6:56:19
2020-08-07 06:56:19
Источники:
Https://math-oge. sdamgia. ru/problem? id=352780
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 338584 решу огэ математика
338584 решу огэ математика
338584 решу огэ математика
Задание 21 № 338584
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 40 минут раньше, чем велосипедист приехал в А, а встретились они через 15 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
Пусть — скорость мотоциклиста, — скорость велосипедиста. Примем расстояние между городами за единицу. Мотоциклист и велосипедист встретились через 15 минут, то есть через часа, после выезда, поэтому Мотоциклист прибыл в B на 40 минут, то есть на ч., раньше, чем велосипедист в А, откуда Получаем систему уравнений:
Скорость мотоциклиста не может быть отрицательной, поэтому скорость велосипедиста равна 1, а время, затраченное на весь путь равно одному часу.
Заметим, что в приведенном решении скорости выражаются не в км/час, а в условных единицах, и зависят от того, за какую величину принято расстояние между городами. Если бы расстояние между городами было принято за 10, то получилось бы V2=10 и V1=30. Однако найденное время не зависит от того, за какую величину принято расстояние между городами.
Приведем другое решение.
Пусть T — время, которое затратил на дорогу мотоциклист. Тогда время, затраченное велосипедистом, равно Пусть S — расстояние между городами, тогда скорость мотоциклиста равна а скорость велосипедиста равна Мотоциклист и велосипедист встретились через 15 минут, то есть через часа, после выезда, поэтому Умножив обе части уравнения на 4 и разделив на S, получим:
Время не может быть отрицательным, следовательно, мотоциклист затратил на дорогу часа, а велосипедист час.
Задание 21 № 338584
Скорость мотоциклиста не может быть отрицательной, поэтому скорость велосипедиста равна 1, а время, затраченное на весь путь равно одному часу.
Oge. sdamgia. ru
27.06.2019 1:59:14
2019-06-27 01:59:14
Источники:
Https://oge. sdamgia. ru/problem? id=338584
Наверх


Решу ОГЭ
Автор 100balnik
Новые тренировочные варианты в формате решу ОГЭ 2022 по математике 9 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ОГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант ОГЭ 2022 №37812183 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812184 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812185 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812186 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812187 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812188 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812189 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812190 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812191 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812192 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812193 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812194 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812195 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812196 с ответами
-
Тренировочный вариант ОГЭ 2022 №37812197 с ответами
Другие тренировочные варианты ОГЭ 2022 по математике:
Пробный вариант №6 ОГЭ 2022 по математике 9 класс 100 баллов с ответами
Вариант Ларина №295 ОГЭ 2022 по математике 9 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
0 комментариев
Inline Feedbacks
View all comments







