Задание 1
В треугольнике $$АВС$$ известно, что $$АС=ВС=9,$$ $$tg A=frac{sqrt{5}}{2}.$$ Найдите $$АВ.$$
Ответ: 12
Скрыть
Пусть $$CH$$ — высота. Так как треугольник $$ABC$$ — равнобедренный, то $$AH=HB.$$
Из треугольника ACH:
$$tg A=frac{CH}{AH}=frac{sqrt{5}}{2}$$
Пусть $$CH=sqrt{5}x,$$ а $$AH=2x.$$ По теореме Пифагора:
$$(sqrt{5}x)^2+(2x)^2=9^2Leftrightarrow 9x^2=9^2Rightarrow x=3$$
Тогда $$AB=4x=12$$
Задание 2
Объем параллелепипеда $$ABCDA_1B_1C_1D_1$$ равен 3. Найдите объем треугольной пирамиды $$AD_1CB_1.$$
Ответ: 1
Скрыть
$$V_1=ABcdot BCcdot BB_1$$
$$V_{ABCB_1}=frac{1}{3}S_{осн}cdot BB_1=frac{1}{3}cdotfrac{1}{2}cdot ABcdot BCcdot BB_1=frac{1}{6}V_1$$
$$V_{AD_1CB_1}=V_1-frac{4}{6}V_1=frac{2}{6}V_1=frac{1}{3}V_1=frac{1}{3}cdot3=1$$
Задание 3
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что неисправная батарейка будет забракована, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,02. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Ответ: 0,0485
Скрыть
Выделим два несовместных исхода, при которых система контроля бракует батарейку:
— батарейка неисправна и она бракуется системой;
— батарейка исправна и она бракуется системой.
Вероятность первого исхода равна $$P_1=0,03cdot0,97,$$ вероятность второго исхода равна $$P_2=(1-0,03)cdot0,02.$$ В результате, искомая вероятность, равна:
$$P=P_1+P_2=0,03cdot0,97+0,97cdot0,02$$
$$P=0,0291+0,0194=0,0485$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 6. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,58
Скрыть
Найдём исходы, когда за 2 броска НЕ набралось более 6 очков:
$$11;12;13;14;15;21;22;23;24;31;32;33;41;42;51$$ — всего 15 исходов.
При $$2^x$$ бросках всего $$6cdot6=36$$ исходов. Тогда в $$36-15=21$$ исходах получили более 6 за 2 броска:
$$P(A)=frac{21}{36}=0,58(3)approx0,58$$
Задание 5
Решите уравнение $$sqrt{-x}=x+6.$$ Если уравнение имеет несколько корней, в ответе укажите их сумму.
Ответ: -4
Скрыть
$$sqrt{-x}=x+6Leftrightarrowleft{begin{matrix} -x=(x+6)^2\ x+6geq0 end{matrix}right.Leftrightarrowleft{begin{matrix} x^2+12x+36+x=0\ xgeq-6 end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} x^2+13+36=0\ xgeq-6 end{matrix}right.Leftrightarrowleft{begin{matrix} x=-4; -9\ xgeq-6 end{matrix}right.Leftrightarrow x=-4$$
Так как -9 не является корнем уравнения, то сумму не находим, тогда ответом будет -4.
Задание 6
Найдите значение выражения $$((sqrt[4]{3}-sqrt[4]{27})^2+7)cdot((sqrt[4]{3}+sqrt[4]{27})^2-7)$$
Ответ: 47
Скрыть
$$(sqrt[4]{3}-sqrt[4]{27})^2=(sqrt[4]{3}^)2−2sqrt[4]{3}cdotsqrt[4]{27}+(sqrt[4]{27})^2=$$
$$sqrt{3}-2sqrt[4]{3cdot27}+sqrt{27}=sqrt{3}-2sqrt[4]{81}+3sqrt{3}=4sqrt{3}+2cdot3=4sqrt{3}-6$$
и
$$(sqrt[4]{3}+sqrt[4]{27})^2=(sqrt[4]{3}^)2+2sqrt[4]{3}cdotsqrt[4]{27}+(sqrt[4]{27})^2=$$
$$sqrt{3}+2sqrt[4]{3cdot27}+sqrt{27}=sqrt{3}+2sqrt[4]{81}+3sqrt{3}=4sqrt{3}-2cdot3=4sqrt{3}+6$$
то
$$((sqrt[4]{3}-sqrt[4]{27})^2+7)cdot((sqrt[4]{3}+sqrt[4]{27})^2-7)=(4sqrt{3}-6+7)cdot(4sqrt{3}+6-7)=$$
$$(4sqrt{3}+1)cdot((4sqrt{3}-1)=(4sqrt{3})^2-1^2=48-1=47$$
Задание 7
На рисунке изображены график функции $$y=f(x)$$ и касательная к нему в точке с абсциссой $$x_0.$$ Найдите значение производной функции $$f(x)$$ в точке $$x_0.$$
Ответ: -2
Скрыть
Значение производной в точке равно значению тангенса между касательной к графику в эту точку и осью $$Ox.$$ Достроим прямоугольный треугольник $$A(0;2); B(0;8); C(3;2)$$
$$tg ACB=frac{AB}{AC}=frac{8-2}{3-0}=2$$
Так как функция убывает, то $$f'(x)=-2$$
Задание 8
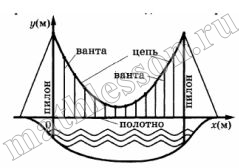
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введем систему координат: ось Оу направим вертикально вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение $$y=0,0041x^{2}-0,71x+34$$, где x и y измеряются в метрах. Найдите длину ванты, расположенной в 60 метрах от пилона. Ответ дайте в метрах.
Ответ: 6,16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$y(60)=0,0041*60^{2}-0,71*60+34=$$$$0,41*36-7,1+34=$$$$14,76-42,6+34=6,16$$
Задание 9
Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве?
Ответ: 172,5
Скрыть
Пусть $$х$$ кг – количество олова в новом сплаве. Так как новый сплав весит 400 кг и в нём находится 30 % цинка, то он содержит $$400cdotfrac{30}{100}=120$$ кг, а во втором сплаве $$(120-y)$$ кг цинка. По условию задачи процентное содержание цинка в двух сплавах равно, следовательно, можно составить уравнение:
$$frac{100y}{150}=frac{100(120-y)}{250}$$
$$frac{y}{150}=frac{120-y}{250}$$
$$5y=3(120-y)$$
$$5y=360-3y$$
$$y=45$$
Из этого уравнения находим, что $$у = 45.$$ Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет $$150cdotfrac{40}{100}=60$$ кг, а во втором сплаве олова будет $$(х-60)$$ кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет $$250cdotfrac{25}{100}=62,5$$ кг.
Во втором сплаве олова содержится $$(х-60)$$ кг, цинка $$120-45 = 75$$ (кг), меди $$62,5$$ кг и, так как весь сплав весит $$250$$ кг, то имеем:
$$x-60+75+62,5=250,$$ откуда $$x=172,5$$ кг
Задание 10
На рисунке изображен график функции $$f(x)=ax^2+bx+c,$$ где $$a,b,c$$ ‐ целые. Найдите $$f(-1).$$
Ответ: 34
Скрыть
Пусть $$f(x)=a(x-m)^2+n.$$ Вершина смещена относительно $$(0;0)$$ на 5 вправо $$Rightarrow m=5$$ и на 2 вниз $$Rightarrow n=-2.$$ Наклон параболы стандартный (соответствует $$y=x^2$$), значит $$a=1.$$ Получим $$f(x)=(x-5)^2-2.$$
Тогда $$f(-1)=(-1-5)^2-2=36-2=34$$
Задание 11
Найдите наибольшее значение функции $$y=sqrt{2lg x-1}-lg x$$
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$${y}’=frac{1}{2sqrt{2lg x-1}}*frac{2}{xln 10}-frac{1}{xln10}=0$$
$$frac{1}{xln 10}(frac{1}{2sqrt{2lg x-1}})=0$$
$$left{begin{matrix}xneq 0 \sqrt{2lg x-1}=1(1)end{matrix}right.$$
$$(1): sqrt{2lg x-1}=1Leftrightarrow$$ $$2lg x-1leq 1Leftrightarrow$$ $$2lg x=2Leftrightarrow$$ $$lg x=1Leftrightarrow x=10$$
$$y(10)=y=sqrt{2lg 10-1}-lg 10=1-1=0$$
Задание 12
А) Решите уравнение $$sqrt{2sin x+sqrt{2}}cdotlog_4(2cos x)=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-pi]$$
Ответ: А)$$-frac{pi}{4}+2pi n;frac{pi}{3}+2pi n,nin Z$$ б)$$-frac{9pi}{4},-frac{5pi}{3}$$
Задание 13
SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN.
А) Доказать, что плоскости SLK и MPN перпендикулярны
Б) Найдите длину отрезка PL, если длина ребра MN равна 4.
Ответ: 3
Задание 14
Решите неравенство: $$2^{frac{x}{x+1}}-2^{frac{5x+3}{x+1}}+8leq2^{frac{2x}{x+1}}$$
Ответ: $$(-infty;-1),[0;infty)$$
Задание 15
15 января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
— 1‐го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
— 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Ответ: 119
Скрыть
Пусть кредит составляет А рублей, 2 % – процентная ставка, 18 месяцев–срок, на который взят кредит.
Ежемесячно нужно выплачивать одинаковую сумму долга $$frac{A}{n},$$
Выплаты процентов составят:
за первый месяц $$0,02cdot А$$ (сумма выплаты идет со всей взятой суммы)
за второй месяц $$0,02cdot(А–(frac{A}{18}))=0,02cdotfrac{17A}{18}$$ (сумма выплат уже уменьшилась на $$frac{1}{18}A$$)
за третий месяц $$0,02cdot(А–(frac{2A}{18}))=0,02cdotfrac{16A}{18}$$ (сумма выплат уже уменьшилась на $$frac{2}{18}A$$)
…
за 18–й месяц $$0,02cdotfrac{A}{18}$$ (сумма выплат уменьшилась на $$frac{17A}{18}$$)
Тогда за 18 месяцев придется вернуть всю взятую сумму
$$18cdotfrac{A}{18}=A$$
и проценты, т.е.
$$0,02cdot А+0,02cdotfrac{17A}{18}+…+0,02cdotfrac{A}{18}=0,02cdot А(1+frac{17A}{18}+frac{16A}{18}+cdots+frac{A}{18})$$
В скобках приводим к общему знаменателю и в числителе находим сумму 18 слагаемых от 18 до 1 по формуле суммы арифметической прогрессии.
$$А+0,02cdotfrac{А(18+17+cdots+1)}{18}=А+0,19А=1,19А$$ руб.– общая сумма выплат
А руб составляют 100%
1,19А руб. составляют х%
$$х=1,19Аcdotfrac{100}{A}=119$$%
Ответ. общая сумма денег, которую нужно выплатить банку за весь срок кредитования 119 % от суммы кредита.
Задание 16
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е
А) Докажите, что AD=CE+CD
Б) Найдите площадь трапеции ABCD, если АЕ=10, $$angle BAD=60^{circ}$$
Ответ: $$frac{25(2+sqrt{3})}{2sqrt{3}}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$(x^2-4ax+a(4a-1))^2-3(x^2-4ax+a(4a-1))-|a|(|a|-3)=0$$
имеет более двух корней.
Ответ: $$(-frac{3}{2};frac{3}{2}),(frac{3}{2};infty)$$
Задание 18
А) В арифметической прогрессии $${a_n}$$ первый член $$a_1=5$$ и разность прогрессии $$d=9.$$ Какие члены прогрессии имеют четное количество делителей?
Б) В последовательности $${x_n},$$ состоящей из целых чисел, известны первые два члена: $$x_1=1, x_2=2,$$ а следующие члены последовательности находятся по формуле $$x_{n+2}=5x_{n+1}-6x_n$$ для всех $$ngeq1.$$ Какой самый большой простой делитель имеет число $$x_{2023}?$$
В) Может ли натуральное число иметь 100 делителей, если сумма его делителей является простым числом?
Ответ: А) все, Б) 2, В) нет
Новый тренировочный вариант №397 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, который вышел на сайте 10 сентября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Демоверсия ЕГЭ 2023 по математике
Тренировочный вариант 397 Ларина ЕГЭ 2023 по математике профиль
ларин-егэ2023-вариант-397-ответы
Ответы для варианта
1)Около окружности, радиус которой равен 8, описан многоугольник, площадь которого равна 208. Найдите периметр этого многоугольника.
Ответ: 52
2)В прямоугольном параллелепипеде АВСDА1B1C1D1 известны длины ребер: АВ = 11, AD = 20, AA1 = 4. Найдите расстояние от вершины С до центра грани АА1D1D.
Ответ: 15
3)Из слова «максимум» случайным образом выбирается одна буква. Найдите вероятность того, что будет выбрана буква, встречающаяся в этом слове только один раз.
Ответ: 0,625
4)Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что извлечённый наугад кубик будет иметь хотя бы одну окрашенную грань.
Ответ: 0,488
9)Имеется три одинаковых по массе сплава. Известно, что процентное содержание никеля во втором сплаве на 25 процентных пункта больше, чем в первом, а процентное содержание никеля в третьем сплаве на 4 процентных пункта больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 64% никеля. Сколько процентов никеля содержит первый сплав?
Ответ: 46
13)В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4. А) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды. Б) Найдите объем пирамиды CDKM.
15)В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы: — каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.; — к июлю 2029 года долг должен быть выплачен полностью. Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму (в тыс. рублей) планируется взять в кредит?
Ответ: 700
16)Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. А) Докажите, что прямые АС и BD параллельны. Б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1.
18)Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из‐за чего количество книг с бирками «выгодно» уменьшилось.
А) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
Б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
В) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки — 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки — 210 рублей. При каком наименьшем количестве книг такое возможно?
Видео решение варианта Ларина
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Задание 1
Решите уравнение $$x^2+log_7 x+log_7frac{7}{x}=50.$$
Ответ: 7
Скрыть
$$x^2+log_7 x+log_7frac{7}{x}=50Leftrightarrow x^2+log_7 x+log_7 7-log_7 x=50Leftrightarrowleft{begin{matrix} x^2+1=50 x>0 end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} x^2=49 x>0 end{matrix}right.Leftrightarrowleft{begin{matrix} x=pm7 x>0 end{matrix}right.Leftrightarrow x=7$$
Задание 2
Наудачу взятый телефонный номер состоит из 5 цифр. Известно, что номер телефона не начинается с нуля. Какова вероятность того, что в нем все цифры нечетные? Ответ округлите до десятитысячных.
Ответ: 0,0347
Скрыть
На 1 месте может быть любая цифра от 1 до 9, то есть 9 вариантов.
На 2, 3, 4 и 5 месте — любая от 0 до 9, то есть по 10 вариантов.
Всего $$9cdot10cdot10cdot10cdot10=90000$$ вариантов.
На каждом месте может быть одна из 5 цифр — 1,3,5,7,9.
Всего $$5cdot5cdot5cdot5cdot5=3125$$ вариантов.
$$P(A)=frac{3125}{90000}approx0,0347$$
Задание 3
В треугольнике АВС угол С равен $$90^{circ},$$ СН — высота, ВС = 17, ВН = 15. Найдите тангенс угла А.
Ответ: 1,875
Скрыть
Так как CH — высота, то треугольник СНВ — прямоугольный, в нём СВ — гипотенуза, ВН и СН — катеты.
Найдем катет СН по теореме Пифагора:
$$СВ^2=ВН^2+СН^2$$
$$289=225+СН^2$$
$$СН^2=64$$
$$СН=8$$
$$ctg B=frac{ВН}{СН}=frac{15}{8}=1,875$$
Так как треугольник АВС — прямоугольный, то $$angle А=90-angle В$$:
$$tg A=tg (90-angle В)=ctg B=1,875$$
Задание 4
Найдите $$frac{3cos a-2sin a}{4sin a+5cos a},$$ если $$ctg a=-3$$
Ответ: 1
Скрыть
$$frac{3cos a-2sin a}{4sin a+5cos a}=frac{3cdotfrac{cos a}{sin a}-2}{4+5cdotfrac{cos a}{sin a}}=frac{3cdot(-3)-2}{4+5cdot(-3)}=frac{-9-2}{4-15}=1$$
$$ctg a=-3Leftrightarrow frac{cos a}{sin a}=-3$$
Задание 5
Найдите объем прямоугольного параллелепипеда $$ABCDA_1B_1C_1D_1,$$ в котором $$ВВ_1=2sqrt{3},АС_1=4sqrt{3},$$ а угол АСВ равен $$30^{circ}.$$
Ответ: 54
Скрыть
Пусть $$AB=x,$$ тогда $$BC=frac{AB}{tg 30}=sqrt{3}x.$$
$$AC_1=sqrt{AA_1^2+AB^2+BC^2}Rightarrow 16cdot3=4cdot3+x^2+3x^2Rightarrow 4x^2=36Rightarrow x^2=9Rightarrow$$
$$Rightarrow x=3$$
$$V=xcdot xsqrt{3}cdot2sqrt{3}=6cdot x^2=54$$
Задание 6
Прямая $$y=8x+11$$ параллельна касательной к графику функции $$y=x^2+7x-7.$$ Найдите абсциссу точки касания.
Ответ: 0,5
Скрыть
Чтобы прямая $$y=8x+11$$ была параллельна касательной к графику функции, необходимо, чтобы их угловые коэффициенты совпадали, то есть были бы равны 8 (множитель перед x). В свою очередь угловой коэффициент касательной к графику функции равен производной функции в соответствующей точке. То есть, чтобы найти абсциссу точки касания, необходимо вычислить производную от функции и приравнять ее 8:
$$y’=2x+7=8$$
$$2x=1$$
$$x=0,5$$
Задание 7
Два тела, массой $$m = 10$$ кг каждое, движутся с одинаковой скоростью $$v = 10$$ м/с под углом $$2a$$ друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле: $$Q = mv^2sin^2a,$$ где $$m$$ — масса в килограммах, $$v$$ — скорость в м/с. Найдите, под каким наименьшим углом $$2a$$ (в градусах) должны двигаться тела, чтобы в результате соударения выделилось энергии не менее 750 джоулей.
Ответ: 120
Скрыть
Выразим квадрат синуса из формулы энергии:
$$sin^2 a=frac{Q}{mv^2}$$
Подставим сюда числовые величины, получим:
$$sin^2 a=frac{750}{10cdot10^2}=frac{3}{4}$$
откуда
$$sin a=pmfrac{sqrt{3}}{2}$$
В задаче спрашивают наименьший угол и в физике углы берутся из положительной области, поэтому имеем уравнение
$$sin a=frac{sqrt{3}}{2}Rightarrow a=arcsinfrac{sqrt{3}}{2}=60^{circ}$$
И, окончательно, угол $$2a=2cdot60^{circ}=120^{circ}.$$
Задание 8
Часы со стрелками показывают 6 ч 15 мин. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?
Ответ: 345
Скрыть
В первый раз стрелки встретятся между 7 и 8 часами, второй раз — между 8 и 9 часами, …, шестой — между 12 и 13 часами. то есть ровно в 13 часов. Таким образом, они встретятся ровно через 5 часов 45 минут, что составляет 345 минут.
Задание 9
На рисунке изображены графики функций $$f(x)=frac{k}{x}$$ и $$g(x)=ax+b,$$ которые пересекаются в точках $$А(-2;3)$$ и $$В(x_0;y_0).$$ Найдите $$x_0.$$
Ответ: 0,75
Скрыть
Прямая проходит через $$(-2;-3)$$ и $$(0;5).$$ Получим:
$$left{begin{matrix} -3=-2k+b 5=0k+b end{matrix}right.Leftrightarrowleft{begin{matrix} -2k=-8 b=5 end{matrix}right.Leftrightarrowleft{begin{matrix} k=4 b=5 end{matrix}right.$$
Гипербола проходит через $$(-2;-3).$$ Тогда:
$$-3=frac{k}{-2}Rightarrow k=6.$$ Получим $$y=frac{6}{x}.$$
$$frac{6}{x}=4x+5Leftrightarrow 4x^2+5x-6=0$$
$$D=25+96=121$$
$$x_1=frac{-5+11}{2cdot4}=frac{1,5}{2}=0,75$$
$$x_2=frac{-5-11}{2cdot4}=-2$$
Задание 10
Известно, что в среднем 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она нестандартна. Найдите вероятность того, что изделие стандартное, если оно прошло упрощенный контроль. Ответ округлите до тысячных.
Ответ: 0,997
Скрыть
Событие А — изделие прошло упрощенный контроль, Г1 – изделие удовлетворяет стандарту, Г2 – изделие бракованное.
$$Р(Г1)=0,95,Р(Г2)=0,05,Р(frac{A}{Г1})=0,95,Р(frac{A}{Г2})=0,06$$
$$Р(A)=Р(Г1)cdot Р(frac{A}{Г1})+Р(Г2)cdot Р(frac{A}{Г2})=0,95cdot0.95+0,05cdot0,06=$$
$$=0,9025+0,003=0,9055$$
$$Р(frac{Г1}{A})$$ – изделие удовлетворяет стандарту, если оно прошло упрощенный контроль.
По формуле Бейеса:
$$Р(frac{Г1}{A})=frac{0,95cdot0.95}{0,9055}approx0,997$$
Задание 11
Найдите точку минимума функции $$y=(x+8)^2cdot е^{-x-3}.$$
Ответ: -8
Скрыть
$$y=(x+8)^2cdot е^{-x-3}$$
Найдём производную функции:
$$y’=((x+8)^2)’cdot е^{-x-3}+(x+8)^2cdot(e^{-x-3})’=2(x+8)cdot e^{-x-3}+(x+8)^2cdot(-e^{-x-3})=$$
$$=e^{-x-3}cdot(2(x+8)-(x+8)^2)=e^{-x-3}cdot(-x^2-14x-48)$$
Найдём нули производной:
$$e^{-x-3}cdot(-x^2-14x-48)=0$$
$$e^{-x-3}>0$$ всегда
$$-x^2-14x-48=0$$
$$x^2+14+48=0$$
Через дискриминант находим корни уравнения:
$$x_1=-8$$
$$x_2=-6$$
Определим знаки производной функции и изобразим поведение функции:
Точка минимума: $$x=-8.$$
Задание 12
А) Решите уравнение $$frac{(x^2-x-12)^2}{x+sqrt{13}}=frac{(2x^2+x-27)^2}{x+sqrt{13}}$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[sqrt{15}-1;sqrt{17}-1]$$
Ответ: А)$$-5;3;sqrt{13}$$ Б)$$3$$
Задание 13
В кубе $$ABCDA_1B_1C_1D_1$$ с ребром, равным 6, на ребре $$АА_1$$ взята точка М так, что $$frac{AM}{MA_1}=frac{1}{2}.$$ На ребре $$D_1C_1$$ взята точка N так, что $$frac{D_1N}{NC_1}.$$
А) Докажите, что прямые $$МВ_1$$ и $$CN$$ перпендикулярны.
Б) Найдите расстояние от точки $$M$$ до прямой $$CN.$$
Ответ: $$frac{2sqrt{2158}}{13}$$
Задание 14
Решите неравенство: $$log_5(sqrt{x^2-7x}+5)>log_{frac{1}{5}}(frac{5}{sqrt{x^2-7x}+sqrt{x+3}+2})+1$$
Ответ: $$[-3;0]$$
Задание 15
15 января планируется взять кредит в банке на сумму 400 тысяч рублей на (n + 1) месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца.
— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
Найдите n, если к 15-му числу n-го месяца за первые n месяцев будет выплачено 424,8 тысячи рублей?
Ответ: 9
Задание 16
В треугольнике АВС угол С — тупой, угол В равен 45o и АН — высота. Прямая АН пересекает описанную около треугольника АВС окружность в точке D.
А) Докажите, что дуги ВC и DA равны.
Б) Найдите ВС, если АС = 8 и площадь треугольника BDH равна 9.
Ответ: $$2sqrt{7}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых неравенство
$$a+|x|+frac{x^2+(a-2)^2}{a+|x|}leq2sqrt{x^2+(a-2)^2}$$
имеет единственное решение.
Ответ: 1
Задание 18
Есть желтые и белые карточки, всего — 100 штук. На каждой написано натуральное число, среднее арифметическое всех чисел равно 32. Все числа на желтых карточках разные. При этом любое число на желтой карточке больше, чем любое число на белой. Все числа на желтых карточках увеличили в 3 раза, после чего среднее арифметическое всех чисел стало равно 94,6.
А) Может ли быть ровно 70 желтых карточек?
Б) Могут ли все числа на белых карточках быть различными?
В) Какое наибольшее количество желтых карточек может быть?
Ответ: А) да, Б) нет, В) 75
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
| 3655 | Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD. Прямые AR и PD пересекаются в точке Q , AD=2BC. a) Докажите, что точка Q – середина отрезка AR б) Найдите площадь треугольника APQ |
Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD ! Тренировочный вариант 221 от Ларина Задание 16 # Решение пункта Б | |
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x).
|
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |

Показана страница 1 из 89
Пробные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Пробные варианты ЕГЭ 2023 по математике (профиль)
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| time4math.ru | |
| вариант 1-2 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2022-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2022-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2022-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2022-yagubov-prof-var36 |
| math100.ru (с ответами) | |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| alexlarin.net | |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий.
Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Связанные страницы:
Пробные варианты ЕГЭ 2022 по математике (профильный уровень)
Сборник задач по стереометрии для 10-11 классов
Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022
Тест по теме «Производная» 11 класс алгебра с ответами
Основные тригонометрические тождества и формулы
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.